數字無絕緣軌道電路調諧單元的諧振分析

姚向明

（北京全路通信信號研究設計院集團有限公司，北京 100073）

數字無絕緣軌道電路調諧單元的諧振分析

姚向明

（北京全路通信信號研究設計院集團有限公司，北京 100073）

介紹數字無絕緣軌道電路S型電氣絕緣節的工作原理，并對調諧單元進行頻率特性和特性阻抗的分析。說明數字無絕緣軌道電路的調諧單元具有良好的選頻特性，并分析改變調諧單元電氣參數所造成的影響。

數字無絕緣軌道電路；調諧單元；頻率特性；特性阻抗

1 研究背景

隨著我國經濟的快速增長，城市人口迅速增加，發展速度快、運量大的城市軌道交通很自然的成了許多城市解決公共交通客運問題的首選方案，它安全、迅速、舒適、便利地在城市范圍內運送乘客，最大限度地滿足市民出行的需要。軌道電路作為城市軌道交通信號系統的一種模式，對保障列車的運行安全、提高列車運行效率起著非常重要的作用。

數字編碼制式的無絕緣軌道電路為電氣隔離式軌道電路，同一個信號點為相鄰兩個軌道區段的分隔點，采用調諧單元構成電氣隔離，是近年來城市軌道交通軌道電路的主要形式之一。其技術先進，通用性強，電路的集成度高，軟件處理能力強。本文以國產化試驗型數字軌道電路為研究背景，在長春輕軌現場參數配置的基礎上，通過對軌道電路調諧單元進行分析，為合理配置傳輸通道中器材參數提供依據，并為數軌的最大有效傳輸提供理論基礎。

2 電氣絕緣節的工作原理

在無絕緣軌道電路中，電氣絕緣節有多種形式。其中，常用的主要有兩種：S型絕緣節和UM71絕緣節。前者主要用在地鐵、輕軌線路上，后者更多地被用在大鐵線路上。S型電氣絕緣節（簡稱S棒）的結構如圖1所示。

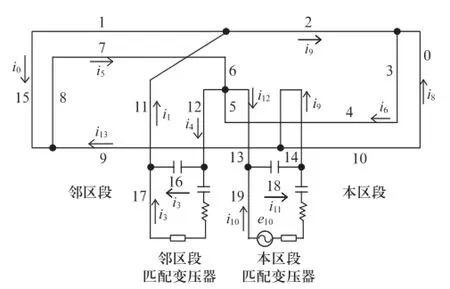
圖1 S棒的等效電路

S棒由兩段鋼軌和一條S型（多股銅絞線）連接線構成。圖1中，支路1、2，9、10各為一段鋼軌，支路3、4、5，6、7、8各為S型連接線的一部分，支路0、15分別表示本區段和鄰區段軌道四端網的輸入阻抗，支路11、12，13、14分別為調諧單元到S棒的引線，C16、C18為調諧電容。

S棒發送端調諧槽路主要由支路6、7、8、9、13、14的電感和支路18的電容C18構成。支路0的兩端是本區段輸出，支路15的兩端是鄰區段輸出。當發送調諧槽路處于并聯諧振時，S棒的輸入阻抗遠遠高于發送器電源的內阻以及信號傳輸電纜的阻抗，從而使發送器輸出的功率主要加在S棒上，保證本區段有較高的信號傳輸比。由于鋼軌支路1和S棒支路7緊密接觸鋪設，兩支路存在互感，使鄰區段輸出降低，保證S棒發送端有很好的隔離性能。

S棒接收端調諧槽路主要由支路2、3、4、5、11、12的電感及支路16的電容C16構成。同一區段內接收端、發送端調諧槽路的參數相同。當接收調諧槽路處于諧振時，接收端有較高的輸入阻抗，保證信號的高效接收。同理，由于鋼軌支路10和S棒支路4緊密接觸鋪設，兩支路同樣存在互感，使接收端鄰區段輸出電壓降低，保證S棒接收端有很好的隔離性能。

由于引線11和引線12緊密捆綁在一起，兩者間的互感應予考慮，互感會減少引線對調諧槽路的影響。同樣也要考慮引線13和引線14的互感。

3 調諧單元的諧振分析

調諧單元結構和等效電路如圖2、圖3所示。對圖3進行簡化，如圖4所示。

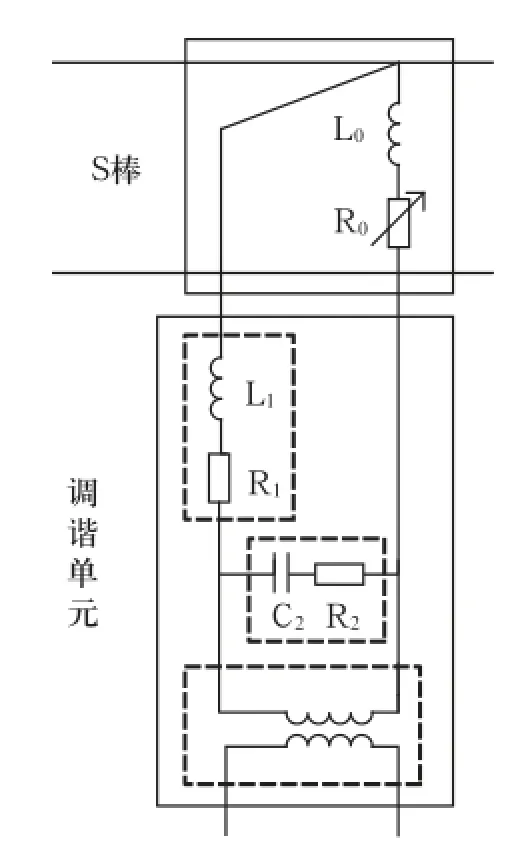
圖2 調諧單元結構示意圖

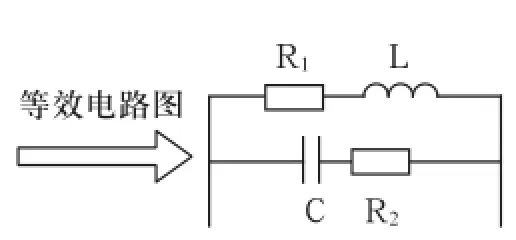
圖3 調諧單元等效電路圖

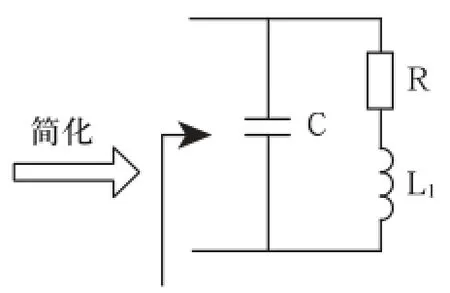
圖4 簡化電路圖

3.1 頻率特性分析

圖3電路發生并聯諧振，因此

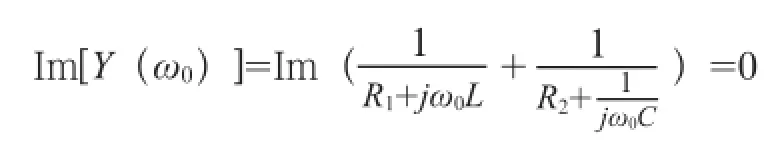
可得，諧振頻率：

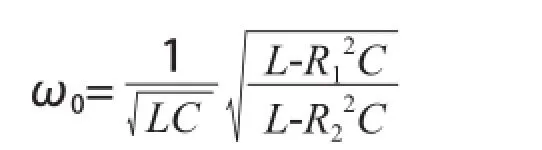
圖4中，由等效變換可得

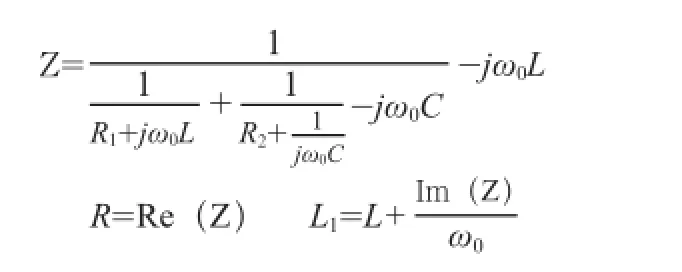
圖4中的并聯諧振槽路的頻率特性如下：

根據上述理論公式，用matlab工具對相鄰軌道電路中心頻率分別為11.5 kHz和13.5 kHz的調諧單元頻率特性進行模擬仿真，結果如圖5所示。

數字無絕緣軌道電路正線軌道電路頻率配置為 9.5、10.5、11.5、12.5、13.5、14.5、15.5、16.5 kHz，頻率相差1 kHz。從圖5可以看出，頻率為11.5 kHz和13.5 kHz的相鄰軌道電路調諧單元的帶寬Bw分別為0.85 kHz和0.859 kHz，均小于1 kHz，說明該軌道電路的調諧單元具有良好的選頻特性和電氣絕緣性能。

3.2 特性阻抗分析

本文以本區段頻率為9.5 kHz為例，由實驗所測各部分參數數據帶入matlab程序中，分析結果如圖6所示。

在現場中，調諧單元與S棒間距離并非絕對相同，若調諧單元與S棒相距較遠，鋼軌接續線較長，相應的R1與L發生變化。在頻率較大時，感抗的影響比電阻的影響更大。等效電路如圖7所示。

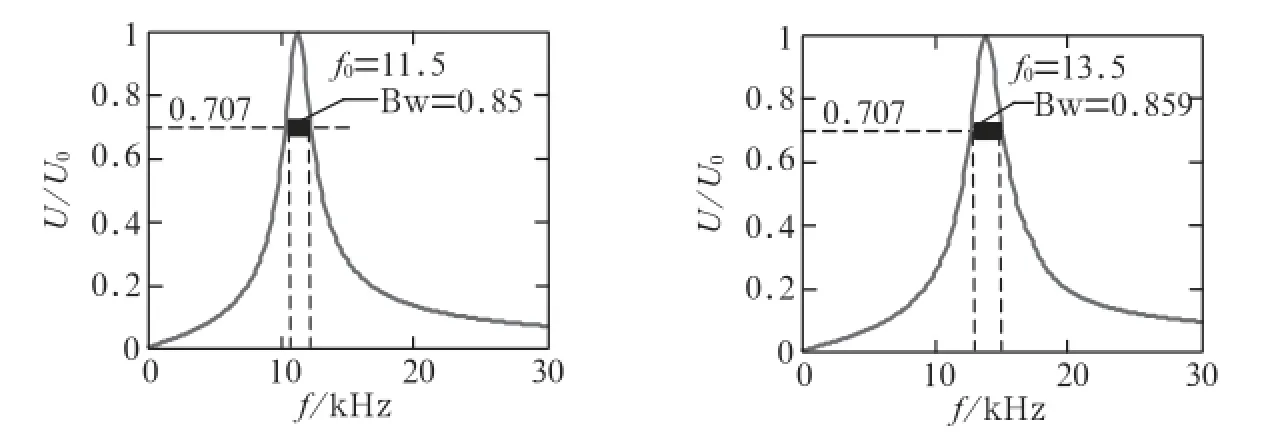
圖5 調諧單元頻率特性（鄰線頻率分別為11.5 kHz和13.5 kHz）

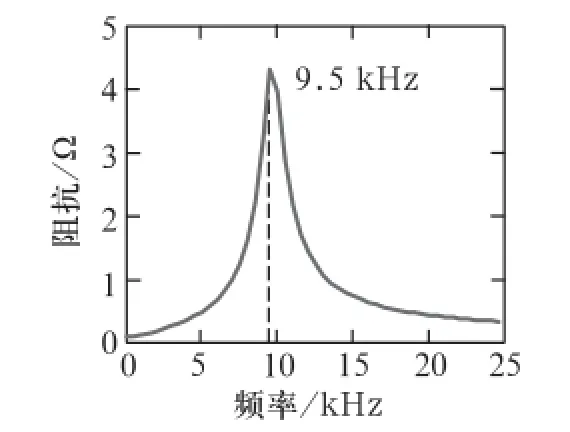
圖6 阻抗-頻率變化曲線圖

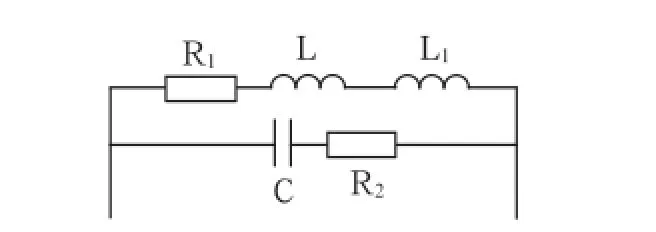
圖7 延長鋼軌接續線等效電路圖

此處在L處再串聯一個小電感L1為1 μH模擬該情形，用matlab進行分析，阻抗隨頻率的變化規律如圖8所示。

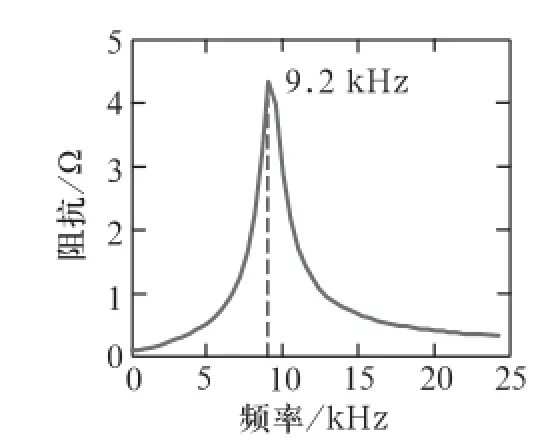
圖8 延長鋼軌接續線阻抗-頻率變化曲線圖

圖8與圖6比較可知，諧振點由9.5 kHz變為9.2 kHz。

在采用新調諧單元中，工藝發生變化，加長了調諧電容的引線長度。相應的R2發生變化，并有感抗出現。在頻率較大時，感抗的影響比電阻的影響更大。等效電路如圖9所示。

圖9 延長電容引線等效電路圖

此處在C的分支再串聯一個小電感L2為1μH模擬該情形，用matlab進行分析，阻抗隨頻率的變化規律如圖10所示。

從圖10可知，諧振點為9.2 kHz，與加長引接線長度對調諧單元的阻抗影響類似。

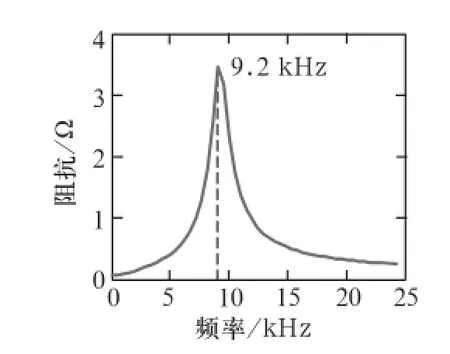
圖1O 延長電容引線阻抗-頻率變化曲線圖

由此可知，現場實際安裝和工藝變化可能造成調諧單元的諧振點發生變化，因此現場安裝情況改變預期時，必須進行分析驗證，必要時重新設置電氣參數。

4 結語

通過對數字無絕緣軌道電路的軌旁調諧單元的頻率特性和特性阻抗進行分析，可以看出，數字無絕緣軌道電路具有較好的絕緣特性，相鄰軌道區段相互影響較小；調諧單元的各部分參數變化均會對諧振產生影響。本文為調諧單元的諧振分析提供一種方法，對軌道電路的分析及指導軌道電路的調整具有現實意義。

［1］鄒雷濱，李曉月，王厲珘.數字編碼制式無絕緣軌道電路調諧單元探析［J］.城市軌道交通研究，2006，9（5）：43-45.

［2］毛廣智，解學書.無絕緣軌道電路系統的圖形建模［J］.計算機工程，2004，30（15）：146-148.

［3］毛廣智，解學書.S型電氣絕緣節的建模與分析［J］.清華大學學報（自然科學版），2004，44（10）：1364-1367.

［4］毛廣智，解學書.S型電氣絕緣節的建模與仿真［J］.鐵道學報，2004，26（1）：45-48.

The paper introduces the principle of S-shaped electrical insulated joints in digital jointless track circuit， and analyzes the frequency characteristics and characteristic impedance of the tuning unit. It explains good frequency selecting characteristics of the tuning unit， and illustrates the impact of changing electrical parameters of the tuning unit.

digital jointless track circuit； tuning unit； frequency characteristics； characteristic impedance

10.3969/j.issn.1673-4440.2015.06.026

2013-02-04）