t分布受控遺傳算法優化BP神經網絡的PM2.5質量濃度預測

荊 濤，李 霖，于文柱，王玉娟，鄭永杰，田景芝

1．齊齊哈爾大學 化學與化學工程學院，黑龍江省 齊齊哈爾 161006

2．齊齊哈爾環境監測站，黑龍江 齊齊哈爾 161000

我國的PM2.5二級標準:年平均質量濃度為35 μg/m3，日均為75 μg/m3［1］。PM2.5主要來源包括煤、石油、汽油、柴油、木材的燃燒，冶煉廠和鋼鐵廠的高溫工業生產過程，汽車排放和生物質燃燒以及植物花粉等［2］。PM2.5能夠散射和吸收光線，造成能見度降低，且濃度越高，能見度越小［3］。PM2.5也可沉積在個人的呼吸道內，引起肺部疾病、心臟疾病和過早死亡［4-5］，且其本身可以吸附大量有害物質，對身體造成危害［6］。因此為了有效保護人類身體的健康，更好地反映大氣污染實時狀況，開展空氣預報是十分必要的［7］，這可以對可能出現的污染狀況及時采取措施，降低空氣污染所帶來的危害。

空氣污染物濃度的預測方法主要分為確定性方法和經驗方法。確定性方法［8］需要詳細的污染來源、排放量的動態信息、排出氣體的化學組成和大氣邊界層的物理過程等信息，這些條件往往難以完全獲取，因此需要近似和簡化模型。經驗方法需要收集大量的監測數據，建立污染物濃度與多種氣象要素或環境因子的線性或者非線性的統計關系，輸出值相對較少，且模型構建簡單。經驗方法比確定性方法更節省時間，且具有更高的精度。常用的經驗方法有多元線性回歸、神經網絡、基因表達式編程算法(GEP)、遺傳-BP神經網絡(BP-GA)等。張本光等［9］對山東省瘧疾高發地區發病率與氣象因子進行多元逐步回歸分析，證明了多元逐步回歸分析適用于多元因素線性關系的預測中。周麗等［10］建立了北京地區PM2.5的粒子濃度與氣象要素的多元線性回歸方程。多元線性回歸不能體現影響因素與PM2.5質量濃度之間的非線性關系，所建立的模型預測結果不準確。劉小生等［11］用基因表達式編程算法(GEP)建立PM2.5質量濃度的預測模型，預測結果表明，用GEP建立的模型預測準確度比較高。白鶴鳴等［12］用BP神經網絡對空氣污染指數預測模擬研究，證明了利用BP神經網絡預測模型對PM2.5濃度的預測也是可行的。Gianluigi等［13］用人工神經網絡模型預測地中海西部2個監測站點的PM10濃度，結果表明，當地的氣象要素和空氣質量起源是模型預測的關鍵性因素，且用神經網絡模型對顆粒物的預測結果比較理想。Grivas等［14］用 4 個網絡模型(MLPf、GA-MLP、MLPnomet、MLR)預測每日PM10質量濃度，預測準確度為MLPf＞GA-MLP＞MLPnomet＞MLR，結果表明，取全部影響因素比用遺傳算法篩選后的因素作為輸入變量的結果更加準確，具有氣象因素的模型預測結果比去除氣象因素后的神經網絡模型預測結果更優越，人工神經網絡模型比多元線性模型對顆粒物的預測結果更加準確。Lovro等［15］用人工神經網絡預測空氣中的污染物(NO2、O3、CO、PM10)，預測精度O3＞NO2＞CO＞PM10，結果表明，用人工神經網絡模型預測空氣中顆粒物PM10的濃度還是有缺陷的，因此模型應該加以改進以提高其預測精度。BP神經網絡具有陷入局部極值、收斂速度慢等缺點，因此BP神經網絡并不能獲得準確的顆粒物PM2.5質量濃度的實時預測。遺傳算法是一種全局優化算法，能夠找出復雜、多波峰，不可微向量的全局最優解，利用遺傳算法來優化BP神經網絡的初始權值能夠保證比較高的概率得到全局最優解。陽其凱等［16］建立了遺傳算法優化BP神經網絡(BP-GA)模型對西安市PM2．5質量濃度進行預測，結果表明，運用此模型基本實現對PM2.5質量濃度的實時預測，然而大量數據的預測準確度低于少量數據。

湯海波等［17-18］建立了氣象因子與空氣污染物及空氣污染指數之間的回歸方程，結果表明，利用氣象要素對空氣污染物預測具有良好的效果。周勢俊等［19］用Kalman方法結合氣象要素實現了大連市的空氣污染預報，也證明了用相應的氣象要素基本可以實現空氣污染物的預測。本文采用t分布變異的思想提出一種t分布受控遺傳算法，結合t分布受控遺傳算法和BP神經網絡算法來對PM2.5質量濃度進行模擬預測，擬建立提高PM2.5預測準確度更優的模型。選取相關的氣象要素，再結合實際的測試條件，選擇大氣壓、溫度、濕度、風速、風向及 SO2、NO2、O3、CO 的濃度作為預測模型的影響因素。

1 t分布受控遺傳算法優化BP神經網絡

1.1 t分布受控遺傳

傳統遺傳算法進化過程為種群的初始化(隨機分布 Xi個體，i=1，2，3，…，N)，適應度計算(個體評價)，選擇操作(群體更新)、交叉操作(更新個體)和變異操作(更新個體)。其中變異操作可增加種群的多樣性，使算法避免陷入局部最優，提高求解速度和精度。但傳統算法的變異操作過于簡單，本文將t分布思想引入變異操作中，提出一種t分布變異方法。

t分布是一種變異擾動性能較優的方法，遺傳算法的變異部分，有用高斯分布和柯西分布改進的［20］，基于柯西分布的鄰域產生小擾動的能力相對于高斯分布有所下降，而產生大擾動的能力有所增強。t分布結合了高斯分布的鄰域小擾動能力與柯西分布的大擾動能力，經過t分布變異的個體比高斯分布及柯西分布更加容易跳出局部最優，提高算法的全局搜索能力［21］。圖1為t分布、標準高斯分布和標準柯西分布的對比曲線圖。

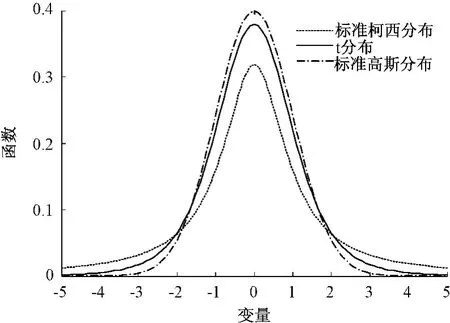
圖1 標準柯西分布、t分布、標準高斯分布概率密度函數曲線

受控衰減算子Φ計算方法見式(1)，表示受控衰減的過程。

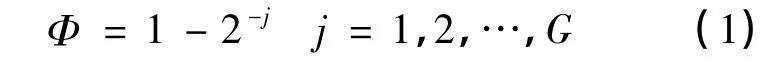
式中j是迭代次數，Φ的值隨著j的值增大而減小，說明隨著迭代次數的增加，受控衰減算子逐漸消亡。

t分布受控遺傳變異對遺傳個體Xi進行t分布變異，執行t分布變異后的遺傳個體，計算方法見式(2)。

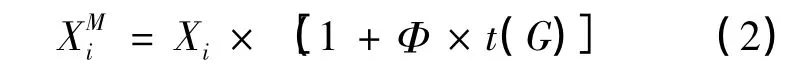
式中t(G)為t分布變量。

1.2 遺傳進化交叉

傳統遺傳算法中交叉概率Pc控制著交叉算子使用頻率，交叉概率越高，群體中結構變化的引入就越快，但已獲得的優良基因結果的丟失速度也相應提高，而交叉概率太低則可能導致搜索阻滯。本文將交叉算子中引入受控衰減算子Φ，使交叉概率在受控衰減算子的控制下執行。

對遺傳個體 Xi按交叉概率進行受控交叉，計算方法見式(3)。

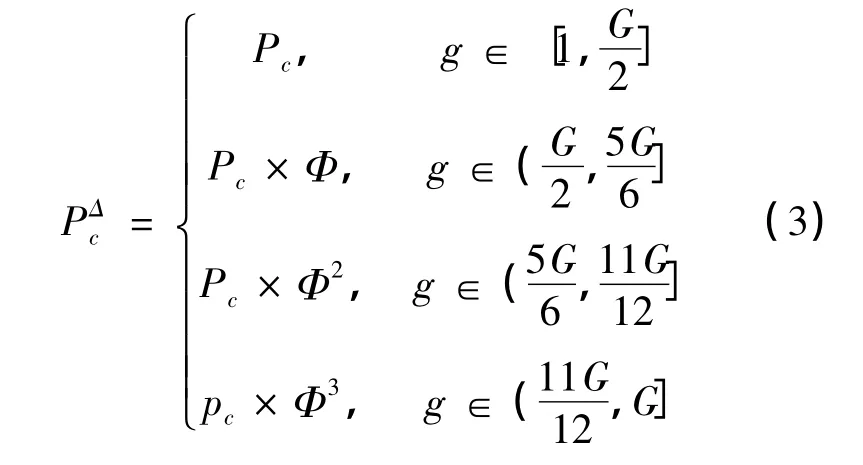
1.3 t分布受控遺傳算法

在t分布受控遺傳算法中，t分布受控遺傳變異取代傳統遺傳變異，受控遺傳交叉取代傳統遺傳交叉，具體算法流程見圖2。

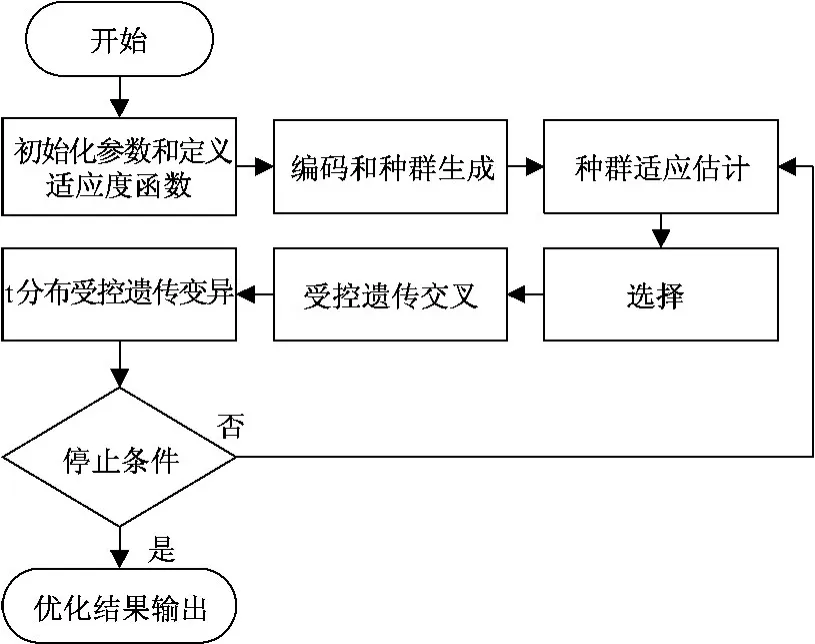
圖2 t分布受控遺傳算法

1.4 基于t分布受控遺傳算法的BP神經網絡模型(BPM-TCG)

BPM-TCG采用t分布受控遺傳算法對BP神經網絡的權值和閾值進行優化，再將其賦予BP神經網絡中進行訓練和預測，以提高BP神經網絡結果的準確性。BPM-TCG見圖3。

圖3 BPM-TCG

1.5 BP神經網絡模型中參數的設定

1.5.1 網絡層數的選擇

BP神經網絡是通過輸入層到中間層、再到輸出層來訓練計算的。隱含層層數增多，會使結果更準確，但卻會增加訓練時間及其訓練的復雜度，而采用3層BP神經網絡能夠實現從m'維到n'維的任意映射［22］。考慮到采取3層BP神經網絡可以滿足所需的精度要求，同時又能減少訓練時間，故隱含層的數目確定為1。本文網絡層數總共分為3層:輸入層1個，隱含層1個，輸出層1個。采用Matlab2011軟件建立1個隱含層的3層BP神經網絡。

1.5.2 傳遞函數的選擇

輸入層tansig;隱含層tansig;輸出層purelin。

1.5.3 訓練函數的選取

通過實驗結果進行對比分析，選擇訓練函數為trainscg。

1.5.4 網絡中各層的節點數選取

輸入層神經元數目為9(相應的影響因素)。輸出層神經元數目為1，即PM2.5的質量濃度。

隱含層神經元數目太小，神經網絡不具備足夠的魯棒性，數目太大會導致訓練時間長，可能導致過度擬合。隱含層節點數的范圍由經驗公式(4)決定［23］。

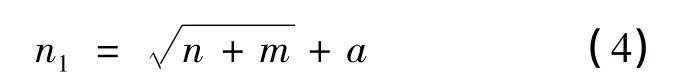
式中:n1為隱含層節點數;n為輸入層節點數;m為輸出層節點數;a為常數，1≤a≤10。

嚴鴻等［24］證明了BP神經網絡隱含層單元數在其經驗公式基礎上擴大，可以尋得最優值。因此，采用式(4)得到隱含層節點數并將其擴大，在擴大的范圍內尋找最優解。

2 結果與討論

2.1 實驗數據

實驗數據來源于2014年3—5月齊齊哈爾大學監測點每小時的PM2.5質量濃度及其對應的影響因素(溫度、濕度、大氣壓、風速、風向)和氣體污染物(SO2、NO2、O3、CO)濃度。

對監測數據進行預處理:去除氣體污染物濃度中的負值和零，去除由儀器所帶來的偶然誤差;如果某組數據缺少一項影響因素或PM2.5質量濃度，則在模型中去除這組數據。篩選后的數據用Excel隨機打亂，以保證樣本的無序性，數據輸入模型前，先對數據進行歸一化處理，減小由數據量綱引起的誤差。訓練樣本和預測樣本以5∶1的比例選取(總樣本數為1 990，訓練樣本數為1 659，預測樣本數為331)。

2.2 隱含層節點參數選取

隱含層節點數選取原則:以訓練樣本相關系數r'及預測樣本相關系數r越大、精度越小、均方根誤差越小越好的原則選擇最佳隱含層節點數。由表1可知，隱含層節點數為18～24時，訓練樣本和預測樣本各種性能參數都在向最優解接近。24個節點和25個節點數對比，訓練樣本相關系數相差不大，而預測效果中25個節點數更優于24個節點數，因此考慮訓練樣本和預測樣本各性能參數，25個節點比24個節點具有更優的解。隱含層節點數大于25時，訓練樣本的相關系數增大，預測樣本的相關系數反而降低了，陷入了過擬合的狀態。綜合考慮，隱含層節點數選擇25。

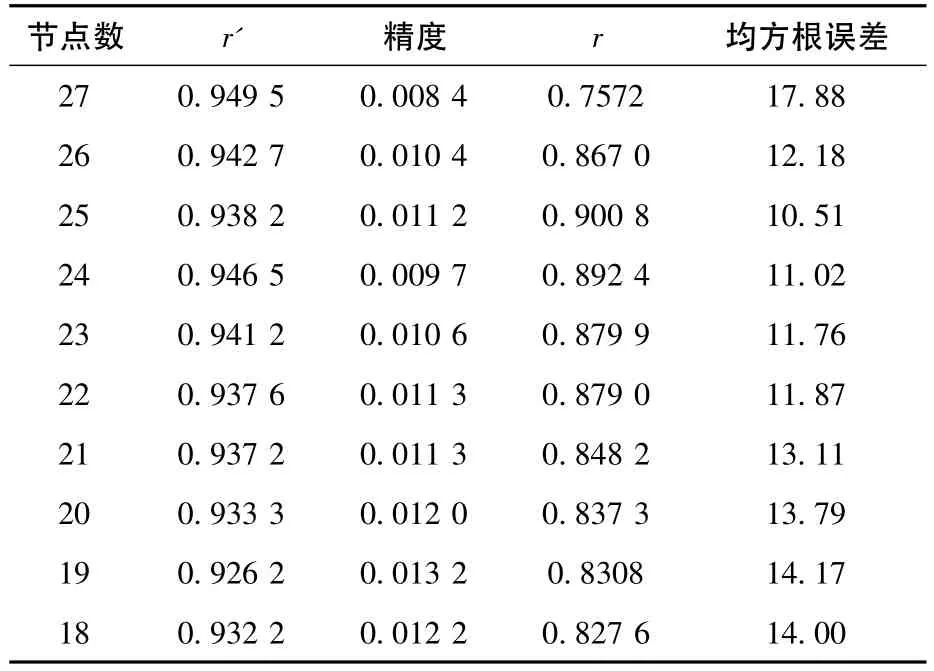
表1 隱含層節點數結果

2.2.2 3種預測模型實驗結果

BP神經網絡模型、BP-GA模型、BPM-TCG模型預測結果分別見圖4、圖5、圖6。

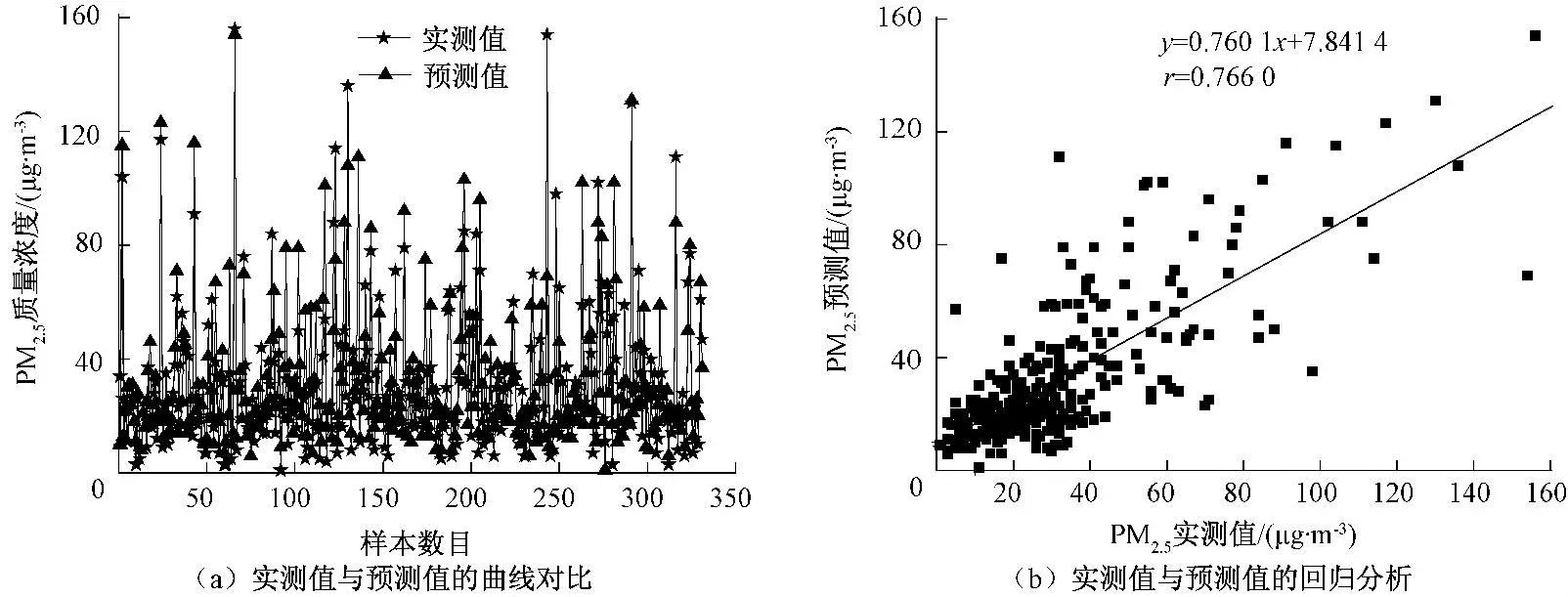
圖4 BP神經網絡模型的預測結果

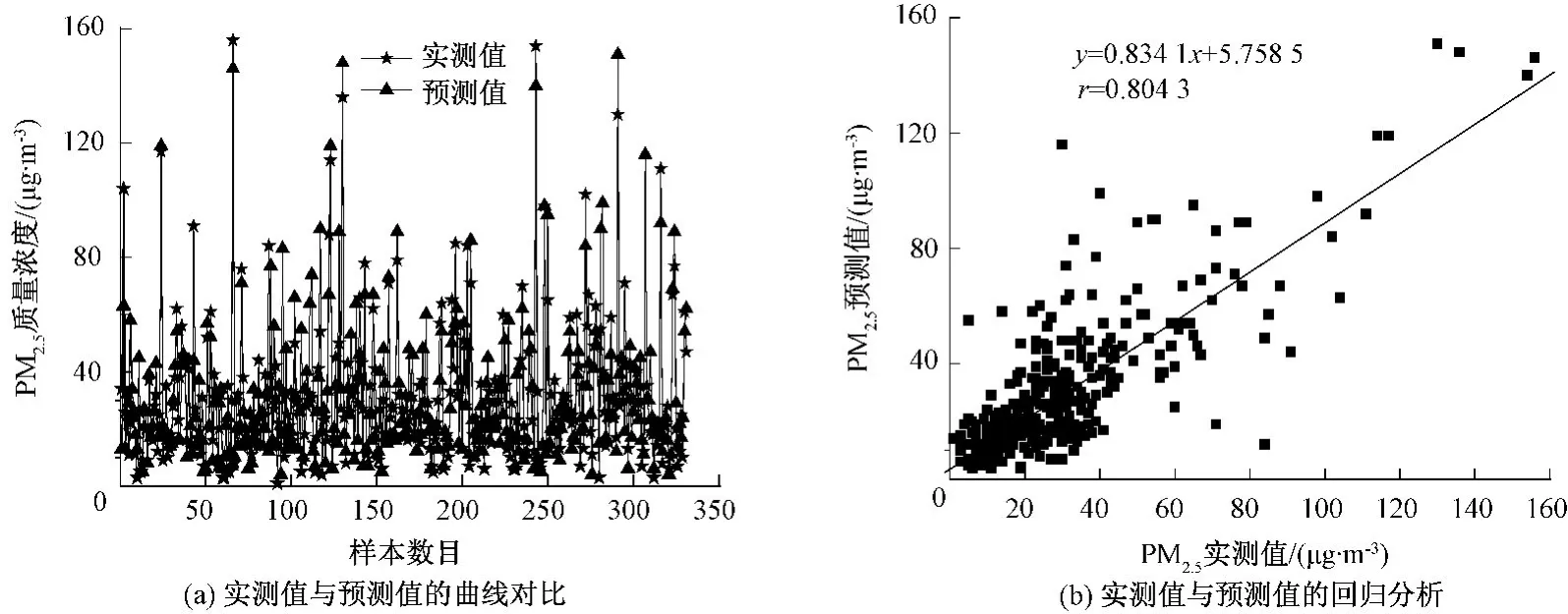
圖5 BP-GA模型的預測結果

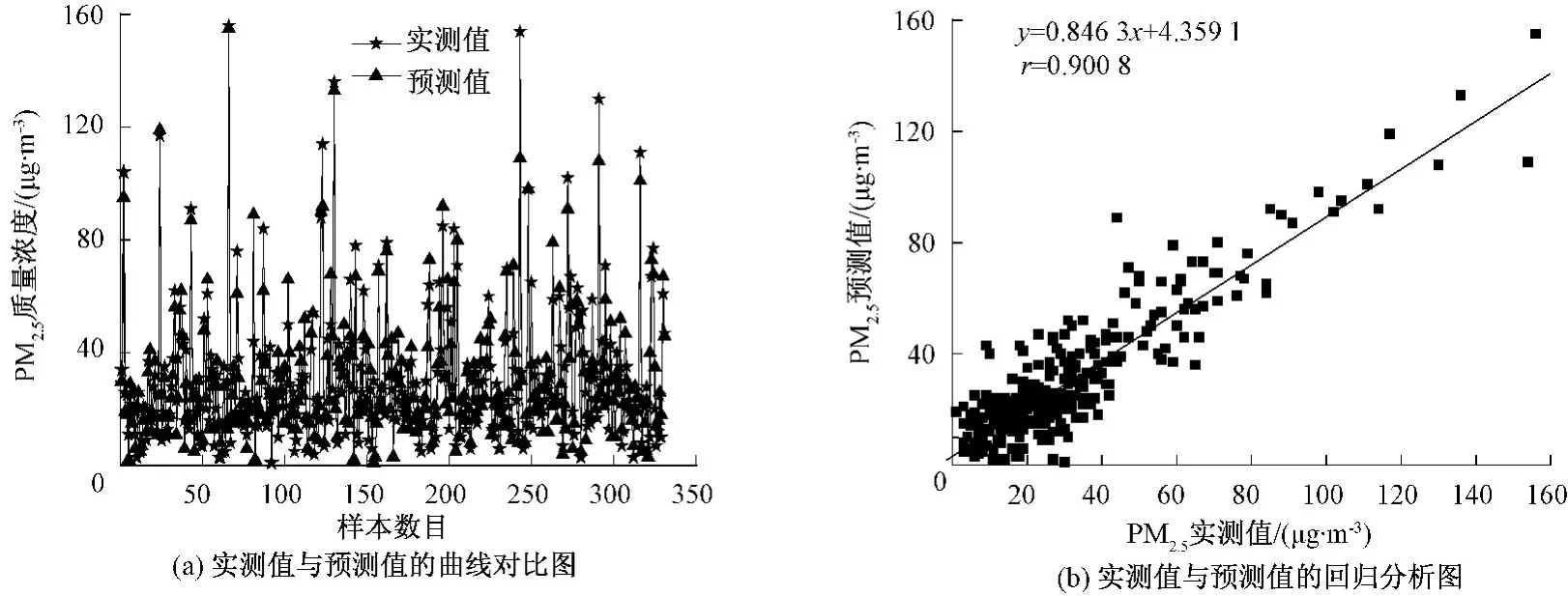
圖6 BPM-TCG模型的預測結果

從圖4(a)、圖5(a)、圖6(a)可見，BPM-TCG模型中的預測值最接近真實值，預測值和真實值數據點基本重合。從圖4(b)、圖5(b)、圖6(b)可見，3種模型的相關系數 r:BPM-TCG＞BP-GA＞BP，BPM-TCG相對于BP和BP-GA模型來說，預測相關系數有了很大提高，且BPM-TCG模型結果中的數據點都集中于期望值1∶1附近，擬合直線與期望值1∶1非常接近，預測結果最好;BP模型預測結果中擬合直線與期望值1∶1偏離程度較大，預測結果最差。

利用這3個模型對預測樣本中超過GB 3095—2012規定的PM2.5質量濃度二級標準的高濃度污染物進行預測，預測結果如圖7所示。由圖7可知，這3種模型中，高污染物濃度的相關系數從大到小順序依次為BPM-TCG＞BP-GA＞BP，BPM-TCG模型對高污染物濃度的預測更為準確。

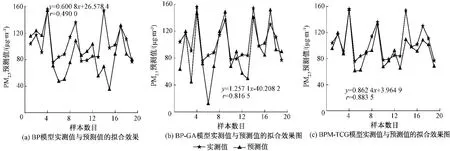
圖7 3種模型的高污染物濃度的預測結果

2.2.3 3種預測模型對比分析

3種模型性能參數如表2所示，表2中均方根誤差(RMSE)和平均絕對誤差(MAE)都以μg/m3為單位計算得到。

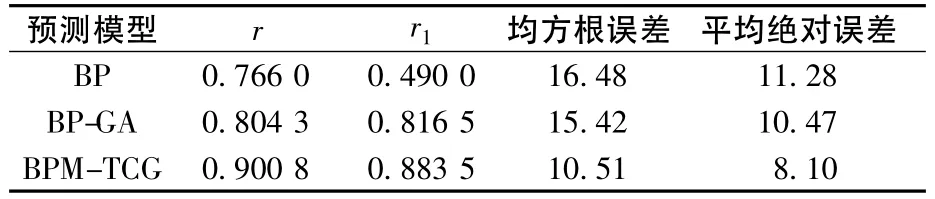
表2 各模型性能參數

從表2可知，3種模型的預測結果中相關系數r從大到小順序依次為BPM-TCG＞BP-GA＞BP;高污染物濃度的預測相關系數r1從大到小順序依次為BPM-TCG＞BP-GA＞BP;均方根誤差從大到小順序依次為BPM-TCG＜BP-GA＜BP;平均絕對誤差從大到小順序依次為BPM-TCG＜BPGA＜BP。

BP-GA模型是以GA優化BP網絡的初始權值，避免BP神經網絡陷入局部極小問題，以達到優化網絡的目的，來提高模型的預測精度。對比表2中BP-GA模型和BP模型的性能參數的結果可知，BP-GA模型優于BP模型，充分體現了利用傳統遺傳算法來搜索BP神經網絡的初始權值比單一BP網絡模型更能夠獲得全局最優解。

BPM-TCG模型是用t分布改進傳統GA的變異操作部分，再用改進的GA來搜索BP網絡的初始權值，以得到更加準確的預測結果。對比表2中 BPM-TCG模型和 BP-GA模型可知，BPMTCG模型各預測性能參數均優于BP-GA模型，這充分體現了結合高斯分布和柯西分布的t分布變異的優越性，BPM-TCG模型比傳統的BP-GA模型能得到更優解，對PM2.5質量濃度的預測結果更加準確。

3 結論

1)對比 BPM-TCG、BP-GA、BP 3種模型預測結果可知，BPM-TCG的相關系數r=0.900 8最大，均方根誤差10.51最小，平均絕對誤差8.10最小，高污染物濃度的預測相關系數r1=0.883 5最大，證明BPM-TCG模型的擬合效果優于BP神經網絡模型和BP-GA模型，BPM-TCG模型更能挖掘出PM2.5質量濃度與其影響因素之間的非線性映射關系。

2)BPM-TCG模型對所有樣本和高污染物樣本的預測相關系數分別為0.900 8、0.883 5，BPMTCG不僅對普通的污染物濃度具有很好的預測準確度，對高污染物濃度也具有很高的預測準確度，證明所選取的氣象因素及其氣體污染物濃度能夠很好地體現PM2.5質量濃度的實時變化情況，BPM-TCG模型對PM2.5質量濃度的準確預測，為PM2.5的預防和治理提供依據。

［1］GB 3095—2012 環境質量空氣標準［S］．

［2］任海燕．認識 PM2.5［J］．中國科技術語，2012，14(2):54-56．

［3］王晨波．PM2.5濃度對能見度影響分析［J］．科技信息，2013，(15):439-440．

［4］Pui D Y H，Chen S C，Zuo Z．PM2.5in China:Measurements，sources，visibility and health effects，and mitigation［J］．Particuology，2014，13:1-26．

［5］Pascal M，Falq G，Wagner V，et al．Short-term impacts of particulate matter(PM10，PM2.5～10，PM2.5) on mortality in nine French cities［J］．Atmospheric Environment，2014，95:175-184．

［6］張文麗，徐東群，崔九思．空氣細顆粒物(PM2.5)污染特征及其毒性機制的研究進展［J］．中國環境監測，2002，18(1):59-63．

［7］佟彥超．中國重點城市空氣污染預報及其進展［J］．中國環境監測，2006，22(2):69-71．

［8］Honoré C，Rouil L，Vautard R，et al．Predictability of European airquality: Assessmentof 3 yearsof operational forecasts and analyses by the PREV’AIR system［J］． Journal of GeophysicalResearch:Atmospheres，2008，113(D4):1-19．

［9］張本光，趙長磊，卜秀芹，等．山東省瘧疾高發地區發病率與氣象因子的多元逐步回歸分析［J］．中國人獸共患病學報，2013，29(3):257-261．

［10］周麗，徐祥德，丁國安，等．北京地區氣溶膠PM2.5粒子濃度的相關因子及其估算模型［J］．氣象學報，2003，61(6):761-768．

［11］劉小生，李勝，趙相博，等．基于基因表達式編程的PM2.5濃度預測模型研究［J］．江西理工大學學報，2013(5):1-5．

［12］白鶴鳴，沈潤平，師華定，等．基于BP神經網絡的空氣污染指數預測模型研究［J］．環境科學與技術，2013，36(3):186-189．

［13］de Gennaro G，Trizio L，Di Gilio A，et al．Neural network modelforthe prediction ofPM10daily concentrations in two sites in the Western Mediterranean［J］．Science of The Total Environment，2013，463:875-883．

［14］Grivas G，Chaloulakou A．Artificial neural network models for prediction of PM10hourly concentrations，in the Greater Area of Athens，Greece［J］．Atmospheric Environment，2006，40(7):1 216-1 229．

［15］Hrust L，Klaic Z B，Krizan J，et al．Neural network forecasting of air pollutants hourly concentrations using optimised temporal averages of meteorological variables and pollutant concentrations［J］． Atmospheric Environment，2009，43(35):5 588-5 596．

［16］陽其凱，張貴強，張競銘，等．基于遺傳算法與BP神經網絡的PM2.5發生演化模型［J］．計算機與現代化，2014(3):15-18．

［17］湯海波，肖培平，楊文增，等．菏澤市氣象因子與空氣質量相關性研究與應用［J］．中國環境監測，2006，22(5):75-78．

［18］邱粲，曹潔，王靜，等．濟南市空氣質量狀況與氣象條件關系分析［J］．中國環境監測，2014，30(1):53-59．

［19］周勢俊，宋煜，吳士杰．Kalman濾波法在城市空氣污染預報中的應用［J］．中國環境監測，2000，16(4):50-52．

［20］吳華偉，陳特放，黃偉明等．一種新的約束優化遺傳算法及其工程應用［J］．計算機應用研究，2013，30(2):367-370．

［21］周方俊，王向軍，張民等．基于t分布變異的進化規劃［J］．電子學報，2008，36(4):667-671．

［22］Nielsen R H． Counterpropagation networks［J］．Applied Optics，1987，26(23):4 979-4 984．

［23］Zhuo L，Zhang J，Dong P，et al．An SA-GA-BP neural network-based color correction algorithm for TCM tongue images［J］．Neurocomputing，2014，134:111-116．

［24］嚴鴻，管燕萍．BP神經網絡隱層單元數的確定方法及實例［J］．控制工程，2009(增刊2):100-102．