單幅圖像運動模糊參數估計

朱建國，樊桂花，劉智超

(裝備學院研究生管理大隊，北京 101416)

圖像復原作為數字圖像處理技術的重要分支之一，其主要目的是盡可能地恢復數字圖像獲取過程中的降質或退化。實際拍攝獲得的圖像往往因為目標與相機之間的相對運動而導致局部相鄰像素加權平均［1-3］，使獲得圖像嚴重偏離真實圖像，將這種圖像降質稱為圖像的運動模糊。為了從一幅運動模糊圖像中獲得原始圖像，必須利用有限的先驗知識從模糊圖像中抽取出圖像的退化信息，從而反向推導估計出原始圖像。

近年來，出現了很多模糊參數的估計方法。M.Cannon等［1］通過對勻速直線運動模糊圖像頻譜圖的分析，證明了條紋方向與運動方向垂直這一特性;陳前榮等［4］通過Hough變換的方法檢測條紋方向，從而獲得模糊角度的估計值，但是準確性有待提高;Krahmer等［5］利用Radon變換的最大熵進行模糊方向鑒別，但是對45°角的估計值存在較大誤差;李秀怡等［6］通過Radon變換求標準差的方法估計模糊角度，但是對存在噪聲的模糊圖像估計存在較大誤差;樂翔、龐濤等［7-8］也利用Radon變換的方法估計運動模糊圖像的模糊角度，但是并未實際考慮圖像的模糊長度;謝偉等［9］提出了一種基于倒頻譜的勻速直線運動模糊PSF估計的方法，利用倒頻譜具有雙負峰值的特性計算運動模糊圖像的模糊方向和模糊長度，但是模糊方向估計上存在一定誤差;倪時金等［10］利用Radon變換和倒頻譜估計的方法估計運動模糊參數，對獲得的倒頻譜圖進行直方圖均衡化和亮度變換以提高檢測精度，但是參數估計精度有待提高;謝飛等［11］利用Radon變換估計模糊角度和求倒頻譜的方法估計喊噪聲圖像模糊長度，但是其主要針對仿真圖像進行分析;石明珠等［12］將梯度倒譜引入模糊估計領域，利用相位恢復策略復原了點擴展函數的相位信息，實現了點擴展函數的快速估計。

以上模糊參數的估計方法或者只估計單一的模糊參數，未考慮全部2個模糊參數，或者同時估計2個參數，但是參數估計精度有待提高。本文主要針對相機實際拍攝圖像的點擴展函數模糊參數估計問題，對點擴展函數的模糊角度和模糊長度分別進行估計，利用改進的Radon變換的方法估計模糊角度，利用改進的梯度倒譜的方法估計模糊長度，并通過R-L(Richardson-Lucy)迭代復原［2］的方法驗證算法的有效性。

1 基于Radon變換的模糊角度估計

1.1 Radon 變換原理

圖像處理中的Radon變換主要是指圖像沿某一指定方向做投影的方法。某一角度函數 f(x，y)沿任意角度可表示為

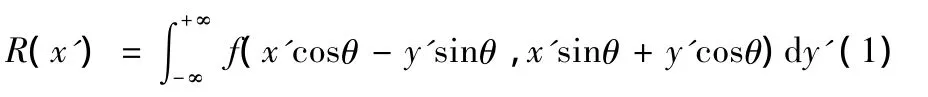
式(1)中所代表的含義是函數 f(x，y)在θ上的投影。在圖像處理中，可以理解為圖像函數 f(x，y)的坐標軸逆時針旋轉角度θ，并對x'進行投影，對獲得累加值順時針旋轉角度θ，獲得了圖像在θ角度的Radon變換。如圖1所示。

圖1 Radon變換示意圖

本文正是利用Radon變換對運動模糊圖像頻譜的每一個方向進行投影，在運動方向上會得到積分的最大值，其所對應的角度就是運動模糊圖像的模糊角度。

1.2 基于Radon變換的改進的運動模糊方向鑒別

真實相機拍攝獲得圖像，由于CCD尺寸問題導致圖像四周邊緣被截斷，這破壞了邊緣的卷積關系，成像的不完全卷積最終導致經中心化的頻譜中央存在十字亮線，嚴重影響模糊方向鑒別精度。

為了盡量仿真真實模糊情況，使模擬圖像中出現十字亮線，在Matlab中，將濾波函數imfilter中的“Boundary Options”設為除“circular”之外的值，本文設定為“replicate”，同時將“Output Size Options”設為“same”，則所得模糊圖像就會出現十字亮線［7］。

本文以Lena512圖像為例，運動模糊長度為20，角度為60°，按照上述方法生成模糊圖像及其頻譜，如圖2所示。

圖2 仿真真實模糊圖像及其頻譜

對上述圖像進行模糊方向估計，得到其對應的幅度譜后，對其進行如圖3所示分塊操作。

圖3 幅度譜圖分塊示意圖

按照上一小節流程最終獲得模糊圖像幅度譜的1/4塊，根據求出的中央十字亮線寬度，對取出的1/4塊進行水平和垂直2個方向裁剪，切除十字中央亮條紋，其結果如圖4所示。

圖4 裁剪前后幅度圖對比

當模糊長度較小時，比如模糊長度為5pixel，暗條紋數目較少，中心主瓣變寬，所取得塊中暗條紋數目極少，其余部分較亮，若此時進行Radon變換，結果誤差會很大，本文對此種情況進行了分析，當獲得塊灰度均值大于130時，應對其進行反色處理。圖5是在模糊長度為5，模糊方向為60°時的幅度譜中取出的1/4塊，未對其做反色處理時，模糊角度估計值為 55.03°，反色處理后結果為 62.1°。

本文在Radon變換的基礎上提出了一種新的模糊方向鑒別算法，有效克服了自然圖像受十字亮線影響而導致的模糊方向鑒別算法失效問題，同時提高了模糊方向鑒別精度，算法具體步驟如下。

設圖像為f(x，y)，圖像尺寸為M×N，則:

1)計算圖像f(x，y)的幅度譜|G(u，v)|，并將其原點位置移到中心位置，仍以|G(u，v)|表示。

2)對|G(u，v)|取對數，B=log(|G(u，v)|+1)，壓縮其動態范圍。

3)對B進行二值化操作，以3×3鄰域求均值作為動態閾值，大于該閾值點賦255值，小于閾值點賦0值，結果矩陣用C表示;

4)將矩陣C劃分為4等分，取右上角部分進行處理，求取中央十字亮條紋寬度。以求十字亮條紋水平寬度為例，計算每行前4個像素和，檢測第一個和大于510時，即前3個像素均為255時，認為是第一條亮條紋;當模糊長度值較小時，則認為僅當每行前4個像素均為255時為第一條亮條紋，假設第一條亮條紋為第i行，則十字亮條紋水平寬度m=M-2i+2，同理可得垂直寬度n=N-2j+2。比較m和n的大小，取其中最大的作為邊界裁剪尺度。

5)仍舊將二值化矩陣劃分為4塊，計算每一塊的灰度值的均值，取最大均值所對應的1/4塊作為待處理部分。這樣操作的目的是選出明暗條紋對比最明顯的塊，即sinc函數主瓣所在的塊。

6)運動模糊尺度較小時，設定閾值T，當取出部分的灰度均值大于T，則對其進行反色處理，使亮暗線相互轉化以提高檢測精度。

7)利用Radon變換將3)中能獲得的結果進行1～179度投影，初始投影間隔為1，獲取其極大值，由文獻［6-8］可知，利用Radon變換檢測到的角度誤差，一般不會超過5°，由此在粗估計角度的基礎上，在其模糊長度范圍內取0.01°間隔進行投影。

圖5 反色處理

2 基于梯度倒頻譜的模糊長度估計

2.1 倒譜的基本原理

倒頻譜指一幅圖像f(x，y)的傅里葉變換的模值取對數后的逆傅里葉變換，其定義最初由Rom提出［13］

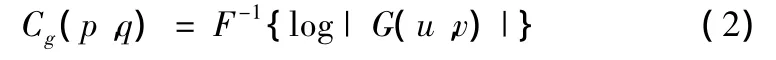
工程應用中一般取如下形式

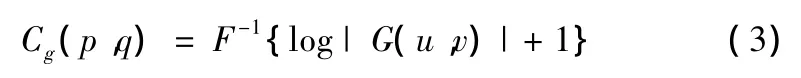
式中:F-1表示逆傅里葉變換;G(u，v)為圖像f(x，y)的傅里葉變換。忽略噪聲影響，將式G(u，v)=F(u，v)H(u，v)帶入式(2)可得

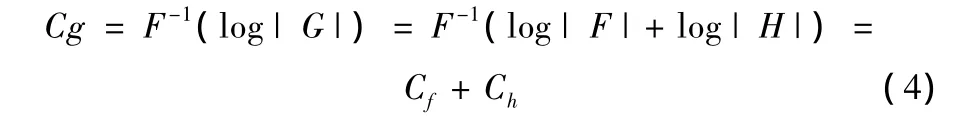
式中:Cf和Ch分別為原始圖像和點擴展函數的倒頻譜。可以看出，通過倒頻譜變換，模糊圖像在倒頻譜域被分解為原始圖像和點擴展函數的倒頻譜之和，頻域的卷積運算變為倒頻譜域的加法運算。

為了更加清晰地顯示倒譜的性質，本文利用Matlab仿真生成了一個中心像素灰度為100、其余灰度為0的40×40像素的圖像，對其加模糊長度為20，角度為45°的運動模糊。其倒頻譜的三維圖如圖6所示。

圖6 倒頻譜的三維圖像

如圖6所示，運動模糊圖像在其倒頻譜域范圍內，圖像信息被分為2部分，高頻成分代表原始圖像特性，低頻成分代表點擴展函數的特性，即模糊特性，由文獻［12］中可知，倒頻譜圖的2個負峰值間的距離即是模糊長度的2倍，2個負峰值點連線與水平方向的夾角即為運動模糊角度。

此外，倒頻譜還有許多與圖像處理有關的［12］，列表如下:

1)將二維卷積運算變為加法運算

2)等角度旋轉性

若在極坐標系內存在 g(r，θ)=Cg(r，γ)則

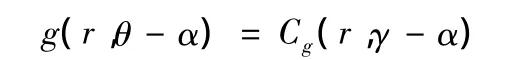
該性質指g旋轉一個角度后求倒譜與其倒譜旋轉相同角度的結果相同。

3)原點對稱性

如果g(x，y)是實函數，其對應的倒譜關于原點對稱

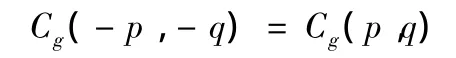
4)周期性

倒譜的以上性質，對于本文提出的基于倒譜的模糊長度估計算法提供了理論依據

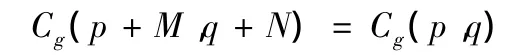
2.2 基于梯度倒頻譜的改進的模糊長度提取算法

本文中降質模型對應的模糊核，即卷積運算中的點擴展函數h(x，y)是相機相對于目標的運動，這是一個隨機的過程，因此其所對應對的二維PSF具有稀疏性和隨機性。倒頻譜不受成像過程中的隨機性影響［12］，對相對運動的隨機性不敏感，因此，通過求模糊圖像的倒頻譜能夠有效分離出PSF信息。如圖7所示。

圖7 圖像倒譜分析

如圖7所示，圖7(a)圖從左至右依次為原始圖像倒譜模值圖、原始圖像梯度倒譜模值圖，圖7(b)圖從左至右為模糊圖像倒譜模值圖、模糊圖像梯度倒譜模值圖以及真實的點擴展函數倒譜模值圖。由圖像上可以看出，梯度倒譜模值圖背景要比圖像倒譜模值圖干凈很多，通過與真實PSF圖像倒譜模值圖對比發現，圖像梯度倒譜模值圖只濾除了圖像信息，成功剝離出模糊圖像的點擴展函數信息。因此，通過模糊圖像的梯度倒譜來估計模糊參數理論上要優于傳統的根據模糊圖像來估計模糊參數的方法。即在點擴展函數的辨識領域，圖像的梯度信息相比于圖像自身，提供了更多的有效信息。拉普拉斯算子被稱為邊界提取算子，其各項同性和平移不變的性質，在邊界提取中具有很好的效果，本文選用八鄰域算子［1，1，1，1，-8，1;1，1，1］。算法流程如下:

1)利用拉普拉斯算子，求模糊圖像梯度，得到梯度圖像g(x，y)。

2)通過式4求梯度圖像倒譜Cg(p，q)，將原點轉移至圖像中心并求其模值，用real(Cg(p，q))表示。

3)對上步獲得的real(Cg(p，q))進行閾值分割，并二值化。本文首先將梯度倒譜模值中大于0的所有像素點賦0值，得到新的矩陣A，尋找到A中的最小值，以最小值0.85倍為閾值進行二值化，定位圖像中的關于圖像中心對稱的兩點。

4)上步獲得的2個兩點即為2個對稱的負峰值(p1，q1)和(p2，q2)位置，則模糊長度為兩點間直線距離的一半，模糊長度由以下公式計算

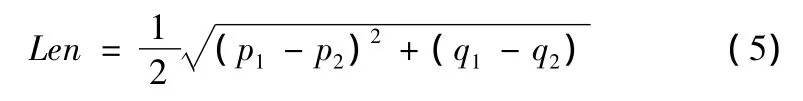
當只檢測到一個點(p，q)時，模糊長度為該點與中心像素之間的直線距離，假設圖像尺寸為M×M時，模糊長度計算公式為

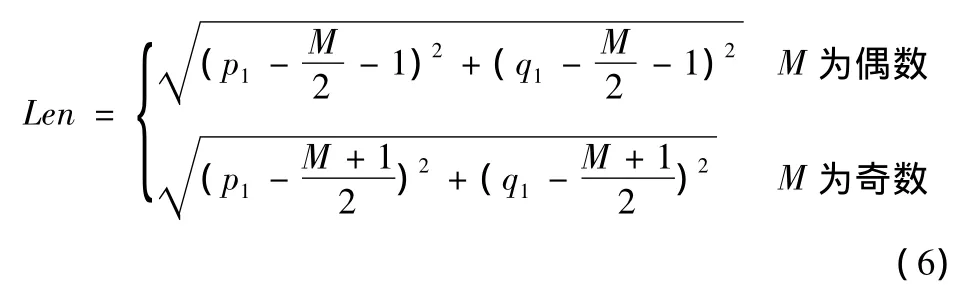
具體流程圖如圖8所示。

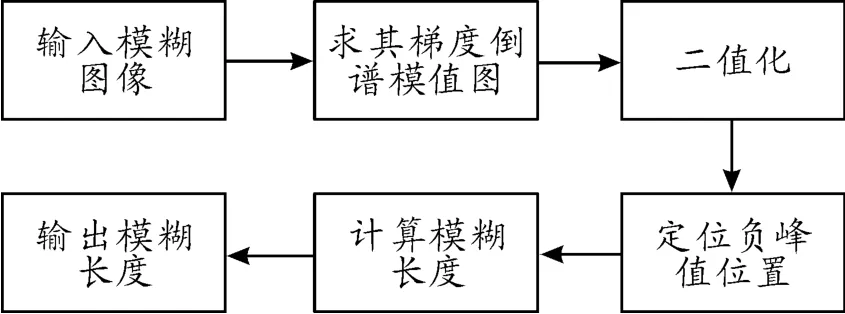
圖8 基于梯度倒譜的模糊長度估計流程

按照上述步驟獲得圖像的模糊長度估計，由圖9(b)中可以看出，直接在圖像的頻率倒譜模值圖中提取圖像負峰值位置，由于圖像亮度過低且彼此間難以分辨，很難實現。利用本文提出的模糊圖像梯度倒譜二值化方法，得到如圖9(c)所示圖像，背景十分干凈，很容易獲得圖像的2個負峰值，根據上文公式就可以獲得圖像模糊長度。

圖9 模糊長度提取的梯度倒譜圖

3 仿真實驗

3.1 仿真實驗分析

為檢驗本文算法的有效性，對Lena512圖像進行仿真實驗，實驗結果分別與文獻［7］和文獻［10］的參數估計值進行對比分析，本文方法獲得的模糊參數及對比文獻的參考數據列表如表1～表4所示，對實際估計值保留一位小數。

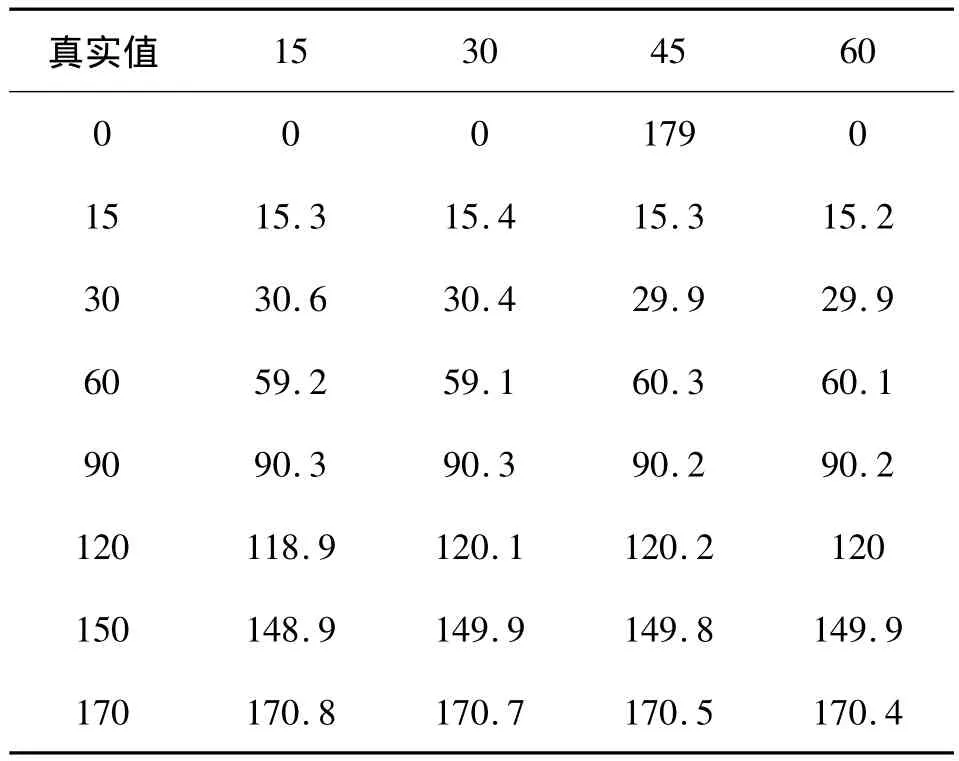
表1 本文Lena512圖像模糊角度估計值 (°)

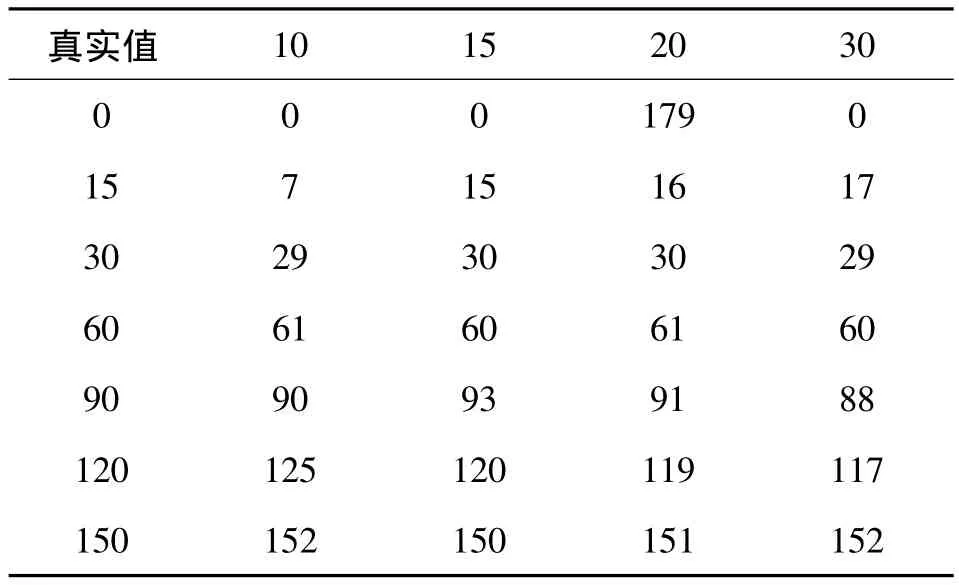
表2 文獻0Lena512模糊方向估計值 (°)

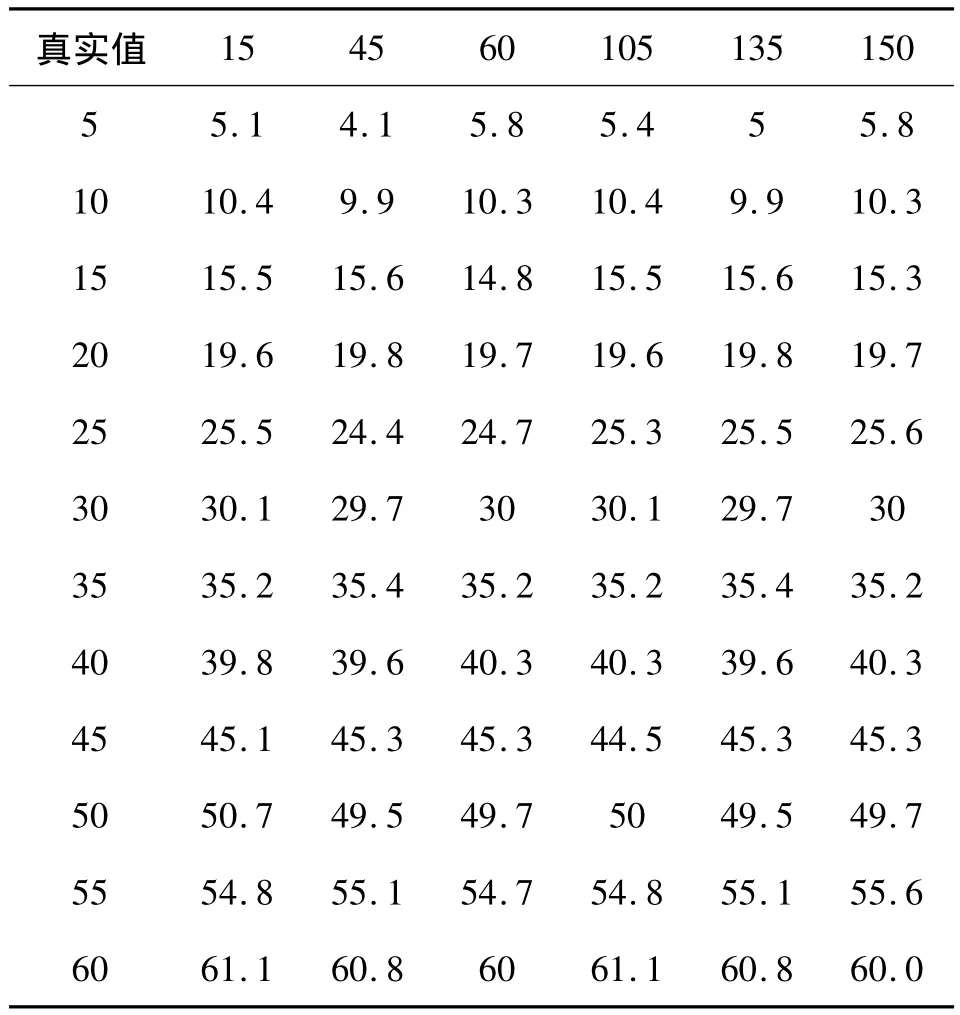
表3 本文Lena512模糊長度估計值 (°)

表4 文獻［10］中Lena512模糊長度估計值 (°)

從表1～表4的數據分析可以看出:

1)本文算法整體上是有效的，模糊角度誤差范圍大多小于1°，且可以最小鑒別5°的模糊角度，模糊長度鑒別誤差基本在1個像素以內，絕大部分誤差小于0.5像素，整體模糊參數估計精度隨模糊尺度的增加，當模糊尺度超過50像素以后，模糊長度鑒別精度開始下降，超過60像素以后，模糊長度和模糊方向鑒別誤差急劇增大，本文認為其估計值失效。

2)由表1和表2對比可以發現，本文算法模糊角度估計精度在0°～1°之間，但存在個別值誤差超過1°，遠優于文獻［10］中的誤差精度。此外，本文算法的探測極限角度為5°，且誤差一般不超過1°，而文獻［7］中的極限探測角度為10°，并存在一定誤差。

3)由表3和表4對以發現，本文模糊長度估計最大估計誤差不足2個像素，有效估計模糊長度范圍為5～60像素，仿真結果遠優于文獻0中結果。

3.2 實拍圖像分析

圖10原圖尺寸為4096×4096圖像，目標靜止，通過移動相機獲得全局模糊圖像，通過截圖獲得目標區域大小為800×800，利用本文算法獲得模糊參數分別為33.0253和39.64°，利用R-L迭代復原算法迭代30次獲得實際復原圖像，紋理信息基本清晰。圖11為實拍玩具汽車運動模糊圖像，原圖尺寸為2160×4096，截取目標區域大小為189×399，本文算法估測結果為18.1324 和 27.64°，利用 R-L 迭代復原算法迭代10次獲得實際復原圖像，整體視覺效果需要進一步改進，但是車輪信息基本清晰。

圖10 實拍運動模糊圖像復原

圖11 實拍運動模糊圖像復原

4 結論

運動模糊參數估計是運動模糊圖像復原的關鍵步驟之一，本文提出了一種檢測出中央十字亮線寬度的方法，在此基礎上，通過對模糊圖像的幅度譜進行分塊裁剪邊緣的方法，濾除了圖像不完全卷積造成的邊緣截斷效應對模糊參數估計的影響，利用Radon變換的方法實現了圖像的模糊角度估計。在模糊長度估計方面，本文利用梯度倒譜不受原始圖像信息干擾的特點，通過查找在梯度倒譜模值圖中查找負峰值的方法估計圖像的模糊長度，取得了較高的鑒別精度。在模糊參數估計的基礎上，對實際拍攝圖像的模糊參數進行檢測，通過R-L迭代復原的方法獲得復原圖像，進一步驗證了算法的有效性。

針對實際圖像的模糊復原，今后的主要工作為:一是提高模糊角度估計的準確性，尤其是針對實際圖像的中央十字亮線估計方法，如何在模糊圖像尺寸較小時，本文中央十字亮線寬度檢測誤差較大;二是有躁圖像的模糊長度估計問題，如何在噪聲干擾下準確提取出負峰值點。

［1］張良培，沈煥峰.圖像超分辨率重建［M］.北京:科學出版社，2012:35-35.

［2］鄧澤峰.圖形復原技術研究及應用［M］.武漢:華中科技大學，2007.

［3］Cannon M.Blind deconvolution of spatially invariant image blurs with phase［J］.IEEE Trans Acoust Speech Signal Process，1976，ASSP 24(1):58-63.

［4］陳前榮，陸啟生，成禮智.運動模糊圖像的運動模糊參數鑒別［J］.國防科技大學學報，2004，26(1):41-45.

［5］Krahmer F，Lin Y，McAdoo B，et al.Blind image deconvolution:motion blur estimation［R］.Technical Report，Institude of Mathematics and its Application，University of Minnesota，2006.

［6］李秀怡，黃繼風.基于Radon變換的運動模糊方向精確估計［J］.計算機科學與工程，2008，30(9):51-53.

［7］樂翔，程建，李民.一種改進的基于Radon變換的運動模糊圖像參數估計方法［J］.紅外與激光工程，2011，40(5):963-969.

［8］龐濤，李小平.基于Radon變換的運動模糊圖像參數估計［J］.科學技術與工程，2010，10(22):5551-5554.

［9］謝偉，秦前清.基于倒頻譜的運動模糊圖像PSF參數估計［J］.武漢大學學報，2008，33(2):128-131.

［10］倪時金，李星野，吳婷婷.運動模糊圖像的PSF參數辨識［J］.計算機工程與應用，2013，49(6):152-155.

［11］謝飛，車宏，蔡猛，等.一種基于倒頻譜鑒別模糊參數的圖像復原算法［J］.電光與控制，2011，18(7):49-54.

［12］石明珠，許廷發，梁炯，等.單幅模糊圖像點擴展函數估計的梯度倒譜分析方法研究［J］.物理學報，2013，62(17):174204-1-11.

［13］Rom R.On the cepstrum of two-dimensional function［J］.IEEE Transactions on Information theory，1975，21(2):214-217.