三角函數的圖象與性質
2015-09-10 07:22:44鄔堅耀
數學教學通訊·初中版 2015年10期
關鍵詞:變形
鄔堅耀

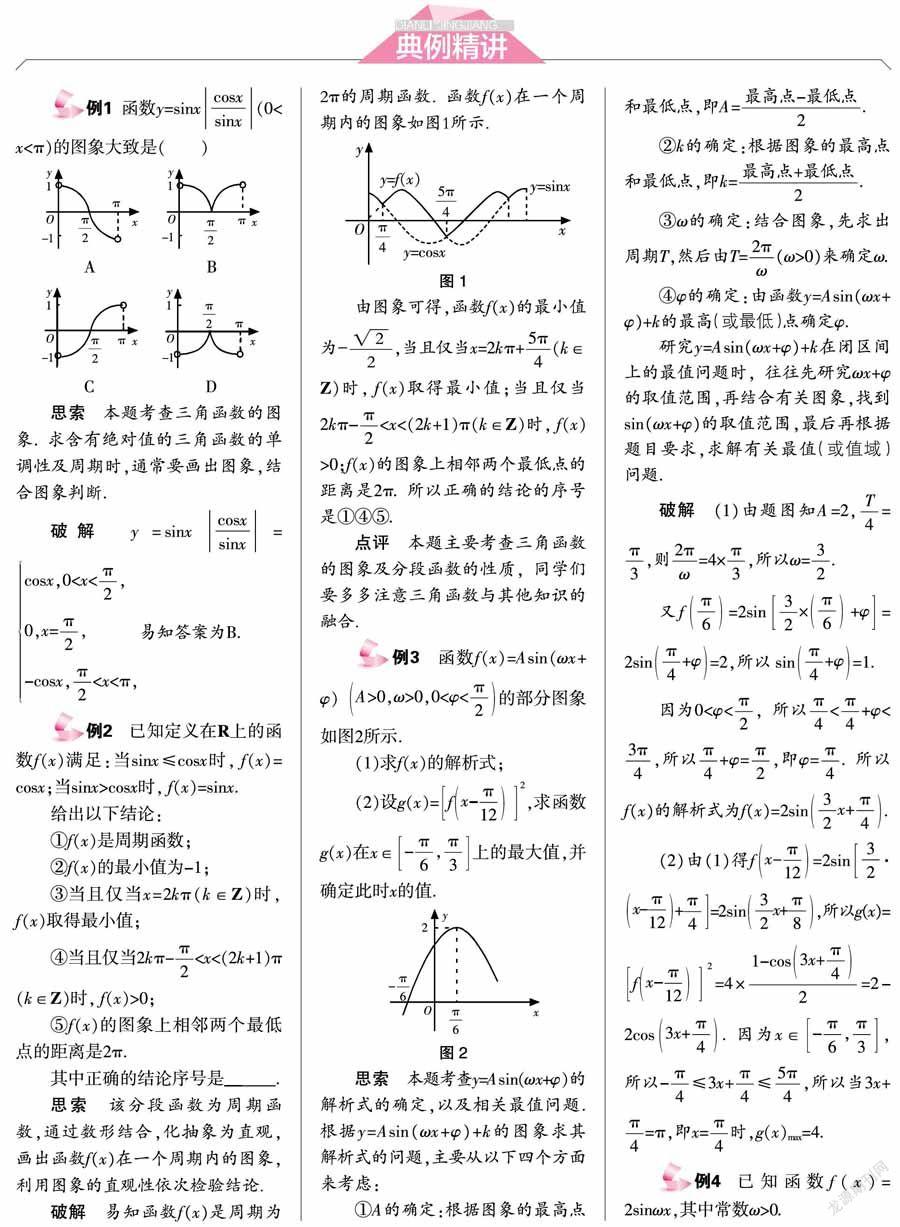

三角函數是描述周期變化現象的重要函數模型,是學習高等數學、物理和應用技術學科的基礎,又是解決生產實際問題的工具.因此,對三角函數的圖象與性質的考查總是每年高考的一個熱點,題型有客觀題和主觀題,主觀題多數處在高考試卷解答題中的中偏易位置,往往與三角恒等變形、解三角形、向量綜合在一起.
重點難點
重點:掌握“五點法”畫三角函數的圖象及其逆向思維,能運用轉化思想,通過恒等變形、換元等方法熟練地求解三角函數的周期、單調區間、奇偶性、對稱性;熟練求解三角函數的值域;理解參數A,ω,φ對函數y=Asin(ωx+φ)的圖象變化的影響以及掌握圖象變換.
難點:函數y=Asin(ωx+φ)的圖象的綜合變換;由函數y=Asin(ωx+φ)的圖象確定A,ω,φ的值或范圍. 前者一般先逆用誘導公式化為同名同號,再分解成若干個中間步驟,并注意變換順序;后者常常以“五點法”中的五個點作為突破口,從圖象的升降情況找準對應的五個點的位置,如何把多對一的問題轉化為一對一的問題,并恰當運用待定系數法是解題的關鍵.
猜你喜歡
智慧少年·故事叮當(2020年10期)2020-11-06 06:19:00
中華詩詞(2020年1期)2020-09-21 09:24:52
河北理科教學研究(2020年1期)2020-07-24 08:14:34
作文成功之路·小學版(2020年11期)2020-02-01 06:26:58
作文周刊·小學二年級版(2018年29期)2018-11-26 11:20:28
小學生作文(中高年級適用)(2018年5期)2018-06-11 01:22:56
童話世界(2018年14期)2018-05-29 00:48:08
數學小靈通·3-4年級(2017年10期)2017-11-08 08:42:59
中學生數理化·七年級數學人教版(2017年11期)2017-04-23 07:18:00
數學大王·中高年級(2016年12期)2016-12-26 21:37:36

