動態學習建構思維本真

姜華

摘要：數學學習是一個動態的自主建構的過程，學生對知識的認知是由淺入深不斷深化的過程，在建構和深化過程中學生的親身體驗非常重要。在計算教學、概念教學、解決問題教學中，學生若以動態的思維方式去發現、組合、交流，創造動態信息，不僅豐富了自身的體驗，還能夠理解知識、發現規律，更能構建自身的動態知識體系，形成動態的思維結構。

關鍵詞：動態化；體驗

中圖分類號：G623.5文獻標識碼：A 文章編號：1992-7711（2015）15-031-2

“什么是數學？”一年級的孩子們給了我很多答案：數學就是要算；數學就是很多數字；數學是最難學的；數學就是這本書……從孩子們童真的回答里我們可以感受到他們對數學的理解，可以感受到“數學”這門學科與他們的心理距離。雖說數學是研究數量關系及空間形式的科學，但是我們不能將這句科學、冷冰的定義呈現給學生。那該如何豐富他們對數學的理解呢？數學是抽象的，而低年級學生的思維特征是以形象思維為主，又該如何打通知識的抽象性和思維的形象性之間的壁壘呢？數學學習過程動態化不失為一個橋梁，可以讓數學學習的過程更具生命力，也能讓學生更好地了解數學，親近數學，喜歡數學。

數學學習動態化意指在動態的學習環境下，學生以動態的思維方式去發現、組合、交流，創造動態的數學信息，從而理解知識、發現規律，溝通知識之間的內在聯系，構建自身的動態知識體系，形成動態思維結構的數學學習方式。

一、計算教學動態化，算理更具象

計算教學在小學數學教學中占有舉足輕重的地位，學生計算技能的強弱在一定程度上影響著他們的數學學習水平。在計算教學中，如果直接告知學生計算法則，然后通過大量計算題強化訓練，雖然學生最終也能學會計算，但是那樣的數學課堂在學生眼中是枯燥的，學生對算法、算理的不理解可能會導致計算的盲目性和機械性，不利于后繼學習。因此，如何幫助學生理解算理，便成了教學的關鍵。但低年級的學生的年齡特征決定了他們的思考方式是以形象思維為主的，這與算理的抽象性形成了鮮明的矛盾，這時可以嘗試將教學過程動態化，以求化解這一矛盾。

例：蘇教版二年級下冊——“隔位退位減”

“隔位退位減”是本冊計算教學的重點，理解隔位退位的算理更是本課的難點。在日常的教學過程中，我們常常會發現很多老師會將這里的隔位退位的過程作狹隘的動態化理解：教學光盤或課件的動畫演示代替了孩子動手撥計數器的過程，在與任課老師的交流中可以歸納出以下幾點主要原因：一、操作學具之后課堂紀律無法掌控；二、動畫演示同樣可以說明算理，比操作學具更省時；三、記住“0上打點想成9”，就突破了計算教學的難點了，多練自會熟能生巧。然而，“動態化”絕非“動畫化”，動畫演示給學生呈現的依然是靜態的學習方式，省時的動畫演示剝奪了孩子通過實踐積累數學活動經驗的機會和權利，使得算理更加抽象，更加冰冷，拒學生于千里之外。

“0上打點想成9”這樣的法則學生真的理解嗎？從后繼的作業反饋中，我們可以發現36人班級有近27%的孩子在計算時并不能主動想起這句話，也許這句話并未真正地走進他們的心底，或者說他們對這句話是不理解的，也就不知道何時能用上這個法則了。

“智慧應該在孩子的指尖上跳躍”。因為在一年級時學生對退位減法已經有一些了解，因此可以首先放手讓學生自己撥一撥計數器嘗試計算。由于每個孩子的學習能力并不等同，此時自主獲得的解決方法也不盡相同。但每個學生都在撥動計算器的過程中積累了疑惑或收獲，在接下來的全班交流與思辨中，算理自然會趨向統一。

二、概念教學動態化，建構更深刻

很多人認為概念教學只要教師講得仔細，學生能記住（背出）概念的定義，然后教師設計練習題，學生在練習中加深、鞏固，這樣就算完成了教學任務。然而事與愿違，許多學生雖然能完整地背出概念，也能在大量變式練習題中掌握概念的含義，但是卻在聯系實際生活解決相關問題時表現出一知半解、邏輯紊亂。

例：蘇教版一年級下冊——“單數、雙數”

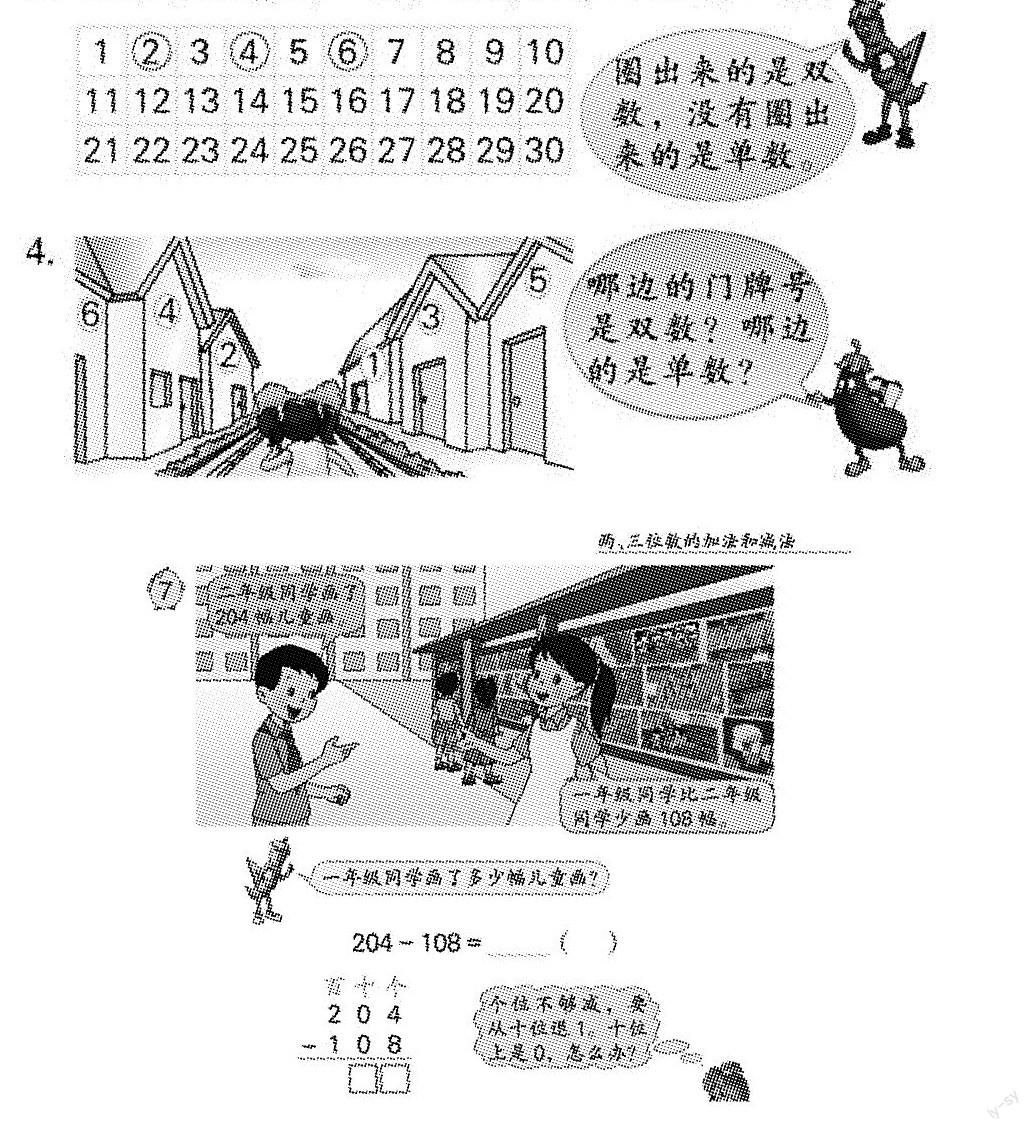
“單數、雙數”的教學，沒有作為獨立的課時，而只是在練習中出現。由于幼小銜接時大量的知識滲透，很多學生對單數和雙數這兩個詞并不陌生，10以內的單、雙數更能脫口而出。因此很多老師將此處的教學作了簡單化的處理，在第3題圈一圈的基礎上，直接告知學生：圈出來的是雙數，沒有圈出來的是單數，然后進行不完全歸納總結單雙數的特點，再迅速進行第4題的練習。整個教學流程在5分鐘之內完成了，但這樣的過程總讓人有種意猶未盡的感覺。就此內容我做了一次學情調查，調查顯示學生有以下三點困惑：一、單數、雙數的概念不明確；二、不能準確地判斷一個數是單數還是雙數；三、不能靈活處理與單雙數相關的實際問題。

在教學過程中，我們常常會被一些假象所迷惑：學生熟悉10以內的單、雙數，會判斷一些數是單數還是雙數，似乎就表示他們明確什么是單、雙數了。那孩子的心中還有疑惑嗎？如果我們和學生換位思考，多問自己一個為什么：“為什么這些數是單數，那些數是雙數？”又會是怎樣的課堂呢？

多問一個“為什么”，就可以讓概念的教學過程動態化，就可以更好地讓學生經歷概念的形成過程，更近地觸及概念的實質。“單數、雙數”的教學過程中，可以讓學生將一定根數的小棒每2根一份分一分，在多次分小棒的過程中，學生會發現：單數根小棒每2根一份，總會剩下1根；雙數根小棒，每2根一份，則正好分完。他們會形象地歸納為：單數根的小棒最后一組總是單獨的1根，沒有朋友；雙數根小棒的每一組都是成雙成對的，沒有孤單的。這些富有童趣的話語里折射出他們對于單雙數的理解。因此在動態化學習基礎上的總結、理解，應用才更深入、更靈活。

三、解決問題教學動態化，思維更生動

解決問題一直是小學數學教學的難點，也是每次學生出錯的“重災區”，究其原因主要是學生不能準確把握數量關系。

例：蘇教版二年級上冊——“求比一個數多（少）幾的實際問題”

教材在練習部分，逐步地穿插了條形圖，突出數形結合的思想。數形結合旨在化難為易，幫助學生把復雜、抽象的數量關系轉化為簡單、直觀的圖形的問題。

這一內容看似簡單，但是在作業反饋中實際的錯誤率很高。很多老師為求得高正確率，常常會總結口訣：多加少減。但是口訣只能解決一些順向描述的問題（如題a），遇到逆向描述的問題時（如題b），學生依然分不清何時用加法，何時用減法。解決實際問題的數學課似乎成了語法課，但結果往往是全然不得法，老師費力、學生無力。

題a：梨子有30個，比桃子少5個，桃子有多少個？

題b：梨子有30個，桃子比梨少5個，桃子有多少個？

試想如果將理解數量關系的過程作動態化的處理，能否對學生的思維能力有所提高呢？孩子天性好玩，好動，容易被一些有趣好玩的事物所吸引。要使孩子輕松有趣地學習數學，可以抓住一點——“玩”，在“玩”中學，使他們覺得學習數學就像玩游戲一般快樂。太極拳法是我國一種古老的拳法，剛柔并濟，推送之間手掌劃過的線條是否形似條形圖呢？于是，理解數量關系的過程中便可以出現“數學太極拳”：第一式：一手推出已知量；第二式：另一手推出和已知量同樣多的比較量；第三式：確定比較量是繼續推出還是收回一部分。“數學太極拳”讓學生樂此不疲，在一次次的推送之間，學生將數量關系理解得更為透徹。

真正意義上的數學學習過程需要擯棄的是“他律”指導下的諄諄說教，需要彰顯的是“自律”意味下的思維本真。學生的數學學習應是一個動態的自主建構的過程，是一個由淺入深不斷深化的過程，在建構和深化過程中他們的親身體驗非常重要，因為沒有親身體驗的知識是空洞的、沒有生命價值的。

數學實際上是一類抽象工具的集合，就如同使用集中了螺絲刀、扳手、鉗子、錘子等的工具盒一樣，老師應該放手讓學生使用這些材料，靈活設計和搭建屬于他們自己的數學大廈。

[參考文獻]

[1]肖川，黃超文主編.盛建武編著.現在，我們這樣做老師.數學卷[M].福州：福建教育出版社，2013.

[2]嚴育洪著.從學生那里學教書[M].重慶：西南師范大學出版社，2010.

[3]張文質著.教育是慢的藝術——張文質教育講演錄（第二版）[M].上海：華東師范大學出版社，2008.

[4]張齊華著.審視課堂 張齊華與小學數學[M].北京：北京師范大學出版社，2010.