高中數(shù)學(xué)中的數(shù)列問題

陳前進(jìn)

數(shù)列是高中數(shù)學(xué)知識體系中一個重要的知識點(diǎn)，它不僅代表著高中數(shù)學(xué)一中與眾不同的思維方式，同時也是對高等數(shù)學(xué)中的矩陣或者行列式等進(jìn)行一個基礎(chǔ)的演示，使學(xué)生提前獲得一些最基本的概念，為日后在數(shù)學(xué)方面的進(jìn)一步學(xué)習(xí)打下一定的基礎(chǔ)。

高中數(shù)學(xué)中數(shù)列知識體系包括了數(shù)列的基本概念、數(shù)列通項式和數(shù)列的擴(kuò)展三個方面。數(shù)列的基本概念已經(jīng)不需要贅言，數(shù)列通項式是數(shù)列中知道數(shù)列中一個數(shù)來求取后一個數(shù)字的規(guī)律，是一個重要的概念和知識要點(diǎn)。求取數(shù)列的通項式有很多的方法例如觀察法、累加法、累乘法、待定系數(shù)法、倒序相加求和法、錯位相減求和法、裂項相消求和法等，涉及到的數(shù)學(xué)思想主要包括函數(shù)與方程思想、分類與討論思想、化歸與轉(zhuǎn)化思想等。

一、數(shù)列通項式的求解方法

函數(shù)通項式是數(shù)列的最重要的特點(diǎn)和概念，就如一個數(shù)列的DNA一樣，用來表明數(shù)列之間本質(zhì)上的不同，同時也成為數(shù)列考試設(shè)計題目的一個重要方式。求解數(shù)列多項式的方法有很多，包括觀察法、累加法、累乘法、待定系數(shù)法、倒序相加求和法、錯位相減求和法、裂項相消求和法等。

1.觀察法求解通項式

給出多項式中的幾個項，然后根據(jù)這幾個項求取中整個數(shù)列的通項式，然后根據(jù)通項式來求解出任意的一個項，這是最容易出題的一個思路和方面，也是最基礎(chǔ)最最重要的方法。

例：給出一個數(shù)列的幾個項如下：1，1，2，3，5，8，x，21，34，55，請跟據(jù)上面的幾個項求出這列數(shù)中的x代表什么？

這個題目雖然簡單，卻是學(xué)習(xí)數(shù)列最基礎(chǔ)最重要的一個范例。事實(shí)上，無論做任何關(guān)于數(shù)列的題目甚至求解任何數(shù)學(xué)題目，對于題目的觀察和對信息的抓取都是最重要的第一步。通過觀察，我們發(fā)現(xiàn)，第三項2是第一項1和第二項1的和，而第四項3又是第二項1和第三項2的和，根據(jù)這個規(guī)律，我們不難發(fā)現(xiàn)，后一個是它本身前兩個之和，于是通項式可以寫作：an=an-1+an-2（n≥2）。根據(jù)這一個范例我們可以舉一反三列出更多的題目，比如已知一列數(shù)為1，1，1，2，3，4，6，9，13，x，28，41，求解x。在這里，我們必須先對數(shù)列中的項進(jìn)行觀察，對于通項式大膽假設(shè)然后小心求證，只要自己的假設(shè)能夠滿足數(shù)列中的規(guī)律，那么自己的假設(shè)可以認(rèn)為是正確的。觀察法和假設(shè)法是求解數(shù)列問題的一個基本方法組合，也是學(xué)生必須掌握的基本技能。

二、與數(shù)列相關(guān)的數(shù)學(xué)思想

在高中數(shù)學(xué)的學(xué)習(xí)過程中，除了掌握一些基礎(chǔ)的數(shù)學(xué)知識和解題技巧以外，對知識和題目之后蘊(yùn)含的數(shù)學(xué)思想進(jìn)行掌握顯得更加重要。那么，與數(shù)列相關(guān)的數(shù)學(xué)思想包括函數(shù)與方程思想、分類與討論思想、化歸與轉(zhuǎn)化思想等。

1.函數(shù)與方程的思想

數(shù)列中蘊(yùn)含的函數(shù)與方程的思想主要表現(xiàn)為在數(shù)列的一些未知項往往以多項式的方式表達(dá)出來，而多項式的表達(dá)往往通過方程的方式，從另一個角度來看，數(shù)列與多項式又都是函數(shù)上的一些不連續(xù)的數(shù)值，也就是函數(shù)圖像上的一些散點(diǎn)，這些散點(diǎn)又有著內(nèi)在的規(guī)律，這個規(guī)律就是前面說到的數(shù)列的通項式。數(shù)列與函數(shù)的結(jié)合通常出現(xiàn)在綜合性較強(qiáng)的題目當(dāng)中。

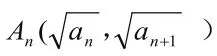
這不僅是一個函數(shù)的問題，同時是一個函數(shù)與雙曲線進(jìn)行結(jié)合的題目，這類題目通常第一問題都比較簡單，也是幫助解題者找到解題道路的一個思路。

an+1-an＝1，所以數(shù)列{an}是以2為首項，以1為公差的等差數(shù)列。

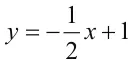
通過函數(shù)與方程的思想將數(shù)列的問題轉(zhuǎn)換為函數(shù)或者方程，有時會轉(zhuǎn)換成為不等式進(jìn)行求解，這是數(shù)學(xué)中的轉(zhuǎn)換的方式，當(dāng)不同的數(shù)學(xué)知識進(jìn)行相互裝換的過程中，對于高中數(shù)學(xué)整體的認(rèn)識會進(jìn)一步得到提升。

2.數(shù)列中的分類與討論思想

分類與討論思想是數(shù)學(xué)嚴(yán)謹(jǐn)性的重要體現(xiàn)，在數(shù)列中也時常體現(xiàn)。討論的對象主要是一些比較特殊的函數(shù)例如對數(shù)中的底不能為1等，或者分段函數(shù)等，都對數(shù)列本身產(chǎn)生較大的影響。

例：已知數(shù)列{an}的前n項和為Sn=1+10n-n2，（1）求數(shù)列{an}的通項公式；（2）求數(shù)列{|an|}的前n項和Tn；

數(shù)列{an}的前n項和為Sn=1+10n-n2是一個開口向下的一元二次函數(shù)，那么在求取通項公式時就分為n=1和n≥2兩種情況；由于函數(shù)的圖像被x軸切割，其絕對值也被分為兩段，這兩段分別為不同的多項式來表示。

三、總結(jié)

高中數(shù)學(xué)中的數(shù)列問題是一個重點(diǎn)知識點(diǎn)，對于很多學(xué)生而言數(shù)列與其他的知識點(diǎn)有形式上的不同，于是就成為了一個難點(diǎn)。在掌握基礎(chǔ)知識和數(shù)學(xué)思想的同時，通過練習(xí)來積累解題的經(jīng)驗(yàn)，通過對這些經(jīng)驗(yàn)的思考來感悟其中的數(shù)學(xué)思想，兩者相輔相成，必然能夠?qū)W好這部分的知識。

[1]史立霞，秦振.數(shù)列中的分類討論問題[M].高中數(shù)學(xué)教與學(xué)，2012（19）.

[2]郭剛.等比數(shù)列的分類討論[M].數(shù)理化學(xué)習(xí)，2012（9）.