基于K-均值聚類算法的西安市汽車行駛工況合成技術研究＊

蔡鍔 李陽陽 李春明 譚曉偉 劉東民

（長安大學）

1 前言

汽車尾氣是城市空氣的重要污染源之一，而不同交通條件下的汽車行駛工況將直接影響尾氣排放。目前，通過對汽車全行駛過程的各運動學片段進行分析，構建一個典型的合成行駛工況并在試驗環境中模擬該工況，是國內外進行尾氣排放測試研究的熱點之一[1～4]。近年來，西安市機動車數量快速增加，汽車尾氣污染已成為突出的環境問題之一，因此研究市區行駛工況對控制汽車排放污染和制定相關政策具有重要意義[5，6]。

本文借助高精度GPS車速儀采集車輛的短行程樣本，并從多參數評價角度出發對短行程樣本進行特征提取，獲取了表征其特性的高維特征值向量。同時，采用核主分量分析（KPCA）實現高維特征向量降維，在消除高維特征值之間冗余量的同時，提取了高維特征值之間的非線性聯系。最后采用基于K-均值的聚類算法對降維后的特征向量進行了分析，獲得了代表市區不同聚類行駛工況的樣本，并且按照離聚類中心最近的原則選擇各聚類的典型樣本合成為西安市汽車行駛工況。

2 原始數據采集

采用英國Race Technology公司生產的型號為DL1 PRO的GPS車速記錄儀（圖1）進行原始數據采集。GPS車速記錄儀內置三軸加速度傳感器，GPS刷新率達20 Hz，通過內置存儲卡可對車輛的行駛速度、加速度、位置信息及模擬量、開關量等多種參數進行實時測量和存儲。由于該設備直接內置加速度傳感器，可以通過加速度值對測量數據進行插補，防止了試驗車輛在城市中因建筑物密集導致GPS信號丟失而引起的數據缺失，保證了采集的原始數據的完整性。為使采集的數據能真實有效地反映西安市道路行駛工況，根據西安城區的分布特點，利用4輛私家車按照各自正常目的地、緊跟行駛車流的方式進行原始數據采集。車輛的行駛范圍涵蓋三環內城區的主要干線道路，時間為早7點至晚8點，采集天數為60天，采樣時間間隔為0.1 s，總行駛里程約為5000 km。

3 汽車行駛工況合成

3.1 短行程特征提取

首先采用短行程法對GPS車速儀原始采集數據進行片段劃分。當車輛速度低于0.5 km/h時，將其定義為車輛怠速狀態，車輛從怠速結束至下一個怠速結束所行駛的距離為1個短行程[7]。將所采集的一段原始車速曲線按照短行程定義進行劃分，共包含7個短行程，如圖2所示。為對短行程數據進行全面評價，從時間、速度和加速度3個方面對所劃分的短行程原始數據進行特征提取，提取的特征參數如表1所列，所得高維特征向量將作為短行程樣本聚類分析的原始數據集。

3.2 基于KPCA的特征參數降維

為全面分析行駛工況數據的分布特點，需要采用盡可能多的特征參數去表征，在獲取全面信息的同時，由于各特征參數之間存在一定的冗余性，如果直接采用高維特征向量進行聚類分析，不僅算法的運算量較大，而且特征的冗余量會導致無法抓住行駛工況的本質信息。因此需要對原始高維特征向量進行降維，在降低運算量的同時消除特征向量之間的冗余性。短行程提取的時間、行駛距離、速度和加速度等特征值之間明顯存在非線性關系，因此采用KPCA對原始特征集進行降維。KPCA是一種非線性降維方法，通過核函數將原始數據從數據空間變換到特征空間，然后在特征空間利用PCA算法進行線性降維。

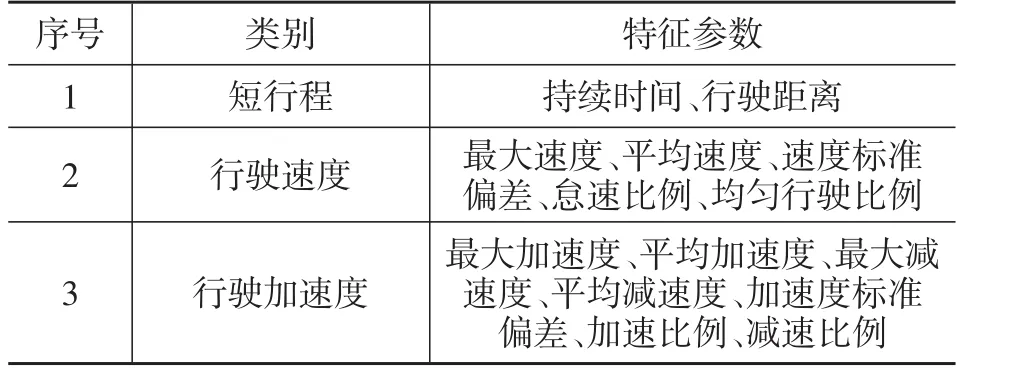
表1 汽車行駛工況特征參數

KPCA的求解步驟[10，11]為:首先通過非線性映射函數φ（x）實現樣本xk∈Rm（k=1，2，…，N）從樣本空間到特征空間的非線性映射，并得到如下協方差矩陣:

得到如下特征值計算式:

式中，R為樣本集合；m為樣本特征數目；N為樣本數目；λi是C的一個非零特征值；ui是對應的特征向量。

通過引入核矩陣K∈RN×N，=，式（1）可轉換為如下特征值計算式:

k（xi，xj）是核函數，本文采用的是高斯核函數:

式中，σ為核函數寬度，將其設置為1。

式（3）的特征值λ1，λ2，…，λd（λ1，＞λ2，…，＞λd）和對應特征向量ξ1，ξ2，…，ξd保留前k（k＜d）個主成分，則yk=（ξ1，ξ2，…，ξk）Tx為降維后數據。

將所采集的行駛工況原始數據進行短行程劃分，共獲得734個短行程，每個短行程按照表1進行特征值提取，在對高維特征集數據歸一化的基礎上對其進行KP?CA降維。由于前5維主成分貢獻量為89.6%，根據主成分貢獻率大于85%的原則[11]，決定保留前5個主成分，并將其作為聚類分析特征集。

3.3 K-均值聚類方法

車輛的設計和開發不能只滿足一種工況，需針對不同交通狀況的多種水平層次的工況來設計[1]。根據提取的行駛工況特征，車輛的行駛工況可劃分為多個類，不同類之間的樣本行駛工況特征差異明顯，而同類樣本的行駛工況特征類似。樣本進行分類后，再從不同類中選取具有代表性的典型樣本，最后構成合成行駛工況。顯然，行駛工況分析是一個典型的無監督聚類問題，在事先不確定樣本類別的前提下，對行駛工況樣本聚類的精確程度將直接影響后續的工況合成。

將K-均值聚類算法用于降維后的短行程工況特征參數聚類。K-均值聚類算法是一種基于樣本間相似性度量的間接聚類方法，目標是最小化所有樣本與之相應的聚類中心之間的距離平方和，屬于非監督學習方法。此算法以k為參數，將n個對象分為k個聚類，使類內樣本具有較高的相似度，而類間樣本的相似度較低。

K-均值聚類算法流程[12]如下:

a.從原數據集S={x1,x2,…,xn}中隨機選取k個輸入初始聚類中心z1,z2,…,zk；

b.根據每個聚類中所有樣本點的均值計算樣本集中每個樣本點與這些均值的距離，并根據最小距離重新對樣本進行劃分；

c.重新計算每個聚類的均值；

d. 循環執行步驟b和c，直到每個聚類不再發生變化為止。

圖3為降維后的前3維短行程特征散點圖，采用K-均值聚類法對所有樣本進行了聚類分析，不同聚類的樣本采用不同顏色表示，每個聚類的中心也被標識。由圖3可看出，短行程特征樣本被有效分為3個聚類。此外，分別計算了第1主成分和表1中每個工況特征參數的相關系數，發現行駛距離L、行駛時間T、怠速比例Tidl、平均行駛速度Vmean、最高行駛加速度Amax等5個特征參數的相關系數超過0.8，表明這些特征參數值與第1主成分值緊密相關，因此可以通過分別計算相同聚類樣本的特征平均值，對短行程聚類結果進行分析。

不同聚類的樣本特征平均值如表2所列，由表2可知，不同聚類的樣本代表不同的短行程工況，各樣本特征平均值差異明顯。其中聚類1樣本的行駛距離和行駛時間最短，怠速比例最高，相應的平均行駛速度和最大加速度最小，表明聚類1樣本為典型的城市擁堵行駛工況樣本；而聚類3樣本特性相反，其行駛距離和行駛時間最長，怠速比例最低，相應的平均行駛速度和最大加速度最大，樣本3應為典型的城市道路通暢行駛工況樣本；聚類2樣本的特性介于聚類樣本1和聚類3樣本之間，其代表的是介于擁堵與通暢之間的城市道路綜合行駛工況樣本。

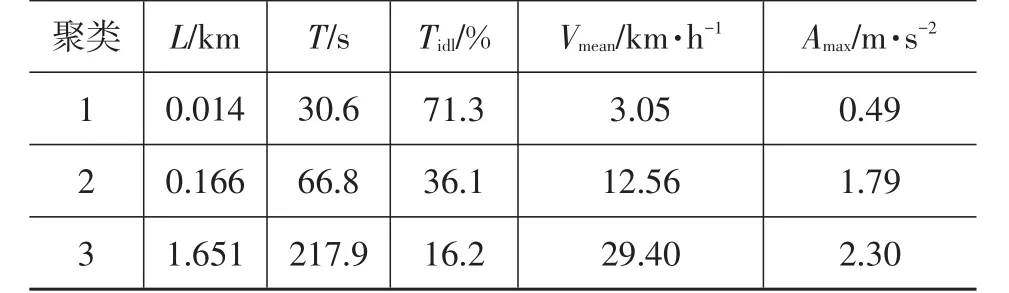
表2 不同聚類的樣本特征平均值

3.4 行駛工況合成

根據短行程特征聚類結果，計算聚類1、2和聚類3的樣本數占總樣本數的比例，分別為12.53%、22.39%和65.08%。分別從不同聚類樣本中選取相應數量且離聚類中心最近的短行程樣本構成各自的合成行駛工況，選擇的短行程數量由該聚類樣本數占總樣本數的百分比和最終合成行駛工況持續時間所決定。合成的擁堵行駛工況、綜合行駛工況和暢通行駛工況的時間-速度曲線如圖4所示。將此3種典型合成行駛工況依次首尾相接，最后合成持續時間為1166 s、平均速度為21.51 km/h、距離為6.9 km的西安市城區合成行駛工況，如圖5所示。

4 合成行駛工況比較分析

計算了西安市合成行駛工況的6個特征參數，并與國外主要行駛工況標準進行了對比，結果如表3所列。

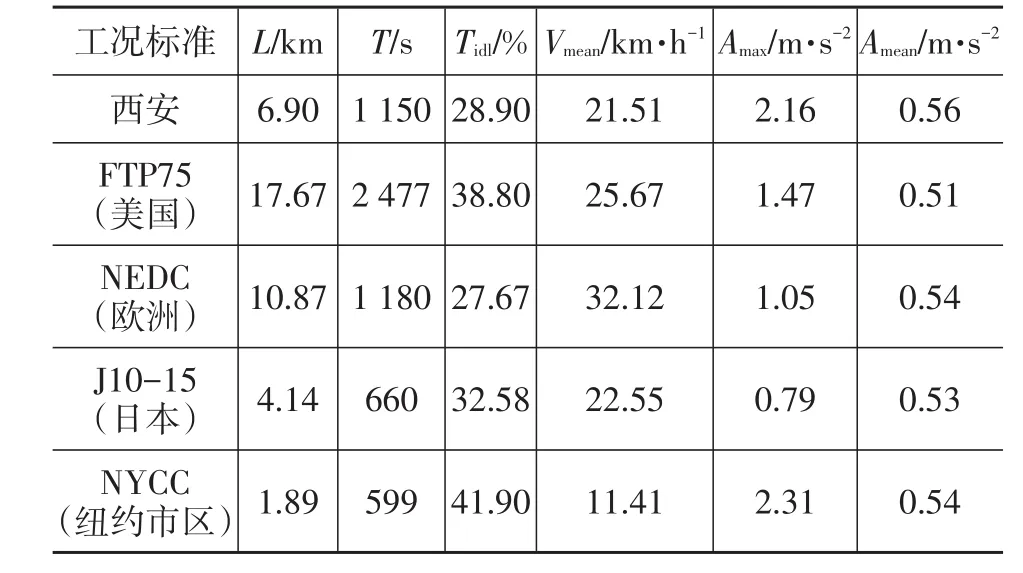
表3 西安市合成行駛工況與國外主要行駛工況標準的特征值比較

由表3可知，西安市合成行駛工況的怠速比例Tidl與其它標準相比較低，最接近于歐洲標準；平均行駛速度Vmean低于其它工況標準，與日本標準相當；最高行駛加速度Amax和平均行駛加速度Amean均高于其它工況標準，與紐約市區標準最接近。總體上評價，西安市工況更接近于日本J10-15標準，但加速度要大很多。

5 結束語

本文借助先進的測試儀器采集了西安市區的汽車行駛工況原始數據。采用短行程法，結合基于KPCA的非線性降維算法和基于K-均值的聚類算法合成了平均速度21.51 km/h、持續時間1166 s、距離6.9 km的西安市城區合成行駛工況。將該工況與其它工況標準對比表明，西安市城區汽車行駛合成工況接近于日本J10-15標準，但具有較大的加速度數值。

1 Zhang Xiao,Zhao DuiJia,Shen JunMin.A Synthesis of Methodologies and Practices for Developing Driving Cycles.Energy Procedia,2012（16）:1868 ～1873.

2 Sanghpriya H.Kamble,Tom V.Mathew,G.K.Sharma.De?velopment of real-world driving cycle:Case study of Pune,India.Transportation Research Part D 14（2009）:132～140.

3 Sze-Hwee Ho,Yiik-Diew Wong,Victor Wei-Chung Chang.Developing Singapore Driving Cycle for passenger cars to es?timate fuel consumption and vehicular emissions.Atmo?spheric Environment 97（2014）:353～362.

4 鄭與波,石琴,王世齡.合肥市汽車行駛工況的研究.汽車技術,2010（10）:34～39.

5 馬洪龍,丁建勛,王桂龍,等.小波變換在道路行駛工況構建中的應用.汽車工程學報,2014（1）:56～60.

6 董恩源,顏文勝,申江衛,等.聚類分析法在城市公交行駛工況開發中的應用.昆明理工大學學報（自然科學版）,2013（5）:41～45.

7 劉希玲,丁焰,我國城市汽車行駛工況調查研究,環境科學研究,2000,1（13）:23～28.

8 Sebastian Mika,Bernhard Sch?lkopf,Alex J Smola,Klaus-Robert Müller,Matthias Scholz,Gunnar R?tsch,Kernel PCA and de-noising in feature spaces,Advances in Neural Information Processing Systems 11（1999）:536 ～542.

9 Fangjun Kuang,Weihong Xu,Siyang Zhang.A novel hy?brid KPCA and SVM with GA model for intrusion detection.Applied Soft Computing,2014,5（18）:178～184.

10 Leonard Kaufman,Peter J.Rousseeuw,finding groups in data:An introduction to cluster analysis,Wiley（1990）.