載貨汽車質量與路面坡度聯合估計方法研究*

李海青 楊秀建 陳蜀喬 高晉

（昆明理工大學）

載貨汽車質量與路面坡度聯合估計方法研究*

李海青 楊秀建 陳蜀喬 高晉

（昆明理工大學）

同時利用縱向動力學模型和加速度偏差坡度估計模型，基于多遺忘因子的遞推最小二乘法（RLS），對載貨汽車的質量與路面坡度進行了聯合估計。在Matlab/Simulink中建立了估計模型,在動力學軟件TruckSim中建立了載貨汽車的非線性車輛模型，通過固定坡度路面與正弦掃頻路面的動力學仿真對估計方法進行了驗證，結果表明，當路面坡度變化不明顯時，使用聯合坡度估計模型與只采用縱向動力學模型對路面坡度進行估計辨識時兩者差異較小；而在正弦掃頻路面條件下，聯合坡度估計模型能夠更好地跟蹤路面坡度變化，估計值更精確。

1 前言

現代汽車的控制系統包含多個子系統，汽車穩定性的控制效果不單純只依靠整車控制器的控制，還需要依賴獲取的車輛參數信息和環境信息。如果能實時準確獲取某些變化或未知的結構參數（如車輛質量）和環境參數（如路面坡度），將能有效改善對汽車穩定性的控制效果。

文獻[1]～文獻[6]針對汽車質量參數的估計方法進行了探討，其中某些文獻[1～4]沒有考慮路面坡度對質量辨識的影響，而有些文獻[5，6]雖同時估計了汽車質量參數和路面縱向坡度，并提出了多遺忘因子的遞推最小二乘法（RLS）估計方法，但僅討論了以縱向動力學坡度估計模型為基礎的質量與坡度聯合辨識，導致坡度估計值在坡度角變化較快時精確度較低。

載貨汽車在運輸過程中質量變化較大，因此對其質量參數進行實時估計辨識很關鍵。為此，本文研究了載貨汽車的質量與路面坡度聯合估計問題，基于汽車縱向動力學模型和加速度偏差坡度估計模型，利用RLS估計方法估計車輛質量和路面縱向坡度。

2 帶遺忘因子的RLS估計方法

RLS估計方法的特點是反復利用實時測量的信息對估計結果進行修正[7]。假設y為實時測量信息，θ為待估計的未知參數，則y可建模為：

式中，y（k）、φ（k）、θ（k）和v（k）分別表示k時刻的測量信息、系數矩陣、待估未知參數和測量誤差向量。

定義殘差成本函數為：

能使殘差成本函數值達到最小時的θ值即為估計值令，則為：

對時變參數而言，過往的殘差信息對當前時刻參數的估計貢獻較小，考慮過多的過往殘差信息在很大程度上增加了計算負擔，因此文獻[7]在RLS估計算法的基礎上引入了針對殘差的指數加權因子又稱為遺忘因子，以淡化與當前時刻距離較遠的殘差信息的影響，形成帶遺忘因子的RLS估計方法，則方程（2）改寫為：

式中，λ為遺忘因子，λ∈（0，1）。

因單個遺忘因子的RLS估計方法不能適應多參數估計中不同參數變化速度存在較大差異的情況，所以文獻[8]提出了多遺忘因子的RLS估計方法，利用該方法可同時估計整車質量和路面坡度。

設存在2個待估計的未知參數θ1和θ2，引入2個遺忘因子λ1和λ2，則式（4）可改寫為：

整理后，可得參數θ1和θ2的估計遞推表達式為：

3 車輛質量與路面坡度估計模型

目前，對車輛質量進行估計時，主要利用縱向動力學模型[1]和橫向動力學模型[2]，對路面坡度估計主要采用基于縱向動力學坡度估計方法與基于加速度偏差坡度估計方法。對車輛質量與路面坡度進行聯合估計時，可以利用縱向動力學模型首先估計出車輛的質量與路面坡度，然后利用聯合坡度估計模型對坡度估計值進行重新濾波。

3.1 縱向動力學質量與坡度估計模型

汽車直線行駛時，縱向加速度與整車質量、路面坡度和動力傳動系統的扭矩輸出存在確定的關系。因此，基于車輛縱向動力學模型可以進行整車質量及路面坡度的估計。當車輛直線行駛時，忽略各車輪的滾動阻力矩，其縱向動力學模型[6]為：

式中，m為汽車的總質量；vx為車速；Fx為驅動力；Te、ωe和Je分別為發動機曲軸的輸出扭矩、轉速和轉動慣量；it和id分別為變速器傳動比和主減速器傳動比；rw為輪胎滾動半徑；Cd、A和ρ分別為氣動阻力系數、車輛的迎風面積和空氣密度；Faero、Ff和Fg分別為空氣阻力、滾動阻力和路面坡度阻力；f為滾動阻力系數；β1為基于縱向動力學的路面坡度；g為重力加速度。

為方便估計算法設計，將式（7）改寫為：

估計算法需要測量發動機輸出扭矩Te、發動機轉速ωe及加速度等參數，通過估計算法可直接估計未知參數θ1和θ2，并由此間接獲得車輛質量m和路面坡度β1。

車輛在行駛過程中采集的參數受環境影響較大，且帶有很強的高頻噪聲，僅利用縱向動力學模型進行坡度估計時會導致路面坡度的估計結果也帶有較大的高頻噪聲，因為此方法主要依賴車輛模型的精度和車輛行駛過程中采集的參數。

3.2 加速度偏差坡度估計模型

加速度偏差坡度估計模型可根據加速度傳感器信號ax和車輛加速度v?x計算路面坡度估計值β2，坡度估計模型為：

式（24）變換后得：

單純的基于加速度偏差的坡度估計方法由于受慣性傳感器的靜態偏差影響較大（慣性傳感器的靜態偏差在計算過程中表現為路面的坡度），且慣性傳感器的靜態偏差屬于低頻信號，此低頻信號將導致路面坡度估計結果不準確[9]。

3.3 聯合坡度估計模型

聯合坡度估計模型將基于縱向動力學的質量與坡度估計模型得到的路面坡度估計值與基于加速度偏差坡度估計模型得到的路面坡度值β2分別進行濾波處理，得到車輛在行駛過程中的實時路面坡度估計值，聯合估計方程[9]為：

式中，τ為時間常數；s為拉普拉斯算子。

4 仿真驗證

利用虛擬試驗仿真對估計方案進行驗證。仿真過程中使用的參考值為TruckSim軟件中車輛模型的設定參數，整車質量的估計值為穩定狀態的均值。整車質量的估計誤差指相對誤差，即估計值與參考值之差的絕對值與參考值的百分比，誤差計算式為：

式中，m為整車質量的參考值，m?為整車質量的估計值。

為得知估計方案的適用范圍，分別進行了固定坡度路面與正弦掃頻路面模擬仿真，根據仿真數據進行參數估計及比較分析。

4.1 固定坡度路面仿真分析

在軟件TruckSim中建立載貨汽車整車仿真模型，在Matlab/Simulink中建立所設計的多遺忘因子RLS估計算法，估計算法所需的ωe、Te、vx、ax等信息直接從TruckSim軟件中獲取。仿真中所用車輛模型的部分參數參考值如表1所列。

在軟件TruckSim中建立的固定坡度路面模型如圖1所示，坡度約為1.75°，氣動阻力系數Cd=0.56，滾動阻力系數f=0.01，空氣密度ρ=1.206 kg/m3，主減速器傳動比id=4.4，初始車速vx（1）=30 km/h，采用7擋自動變速器。估計誤差協方差矩陣的初值為：P1（1）=100，P2（1）=100；參數估計的初值為：θ1（1）=0.000 02，θ2（1）= 0.050 00；遺忘因子的大小與該參數的變化范圍有關，當參數固定不變時可取最大值1，遺忘因子不宜取的太小，否則會導致算法失效。由于整車質量變化較小，故質量估計遺忘因子λ1=1，又因路面坡度變化也較小，故設坡度估計遺忘因子λ2=0.95，時間常數τ=0.1。參數估計過程中的發動機輸出扭矩、車速和加速度如圖2所示，其中在仿真進行至第5 s時變速器處于4擋（it=2.25）位置，而在約第13 s時變速器進入5擋（it=1.5）。

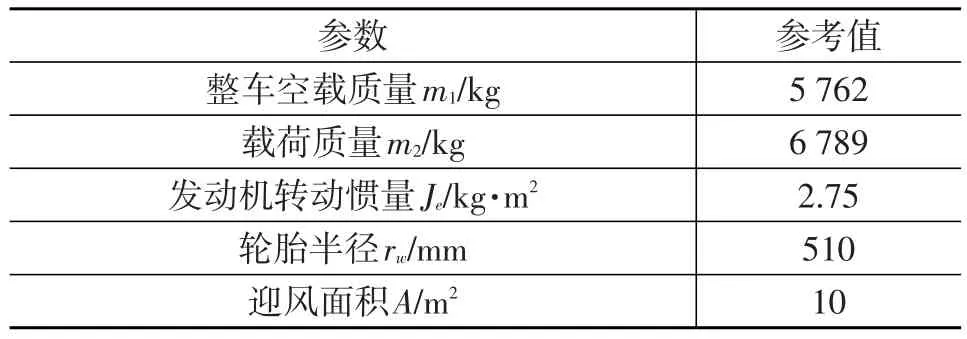
表1 車輛模型部分參數參考值

基于縱向動力學模型的整車質量和路面坡度的估計結果分別如圖3和圖4所示。由圖中可看出，整車質量的估計值約為kg，整車質量的參考值為m=1.255×104kg，則整車質量估計值的相對誤差在5%以內，坡度參數的估計值與實際值相比誤差較小。基于聯合坡度估計模型的路面估計結果如圖5所示。由圖4和圖5可看出，坡度值變化較小時，2種坡度估計模型的估計結果差別較小。

4.2 正弦掃頻路面仿真分析

在模型TruckSim中建立的正弦掃頻路面模型如圖6所示，因為正弦掃頻路面坡度變化較大，故設坡度估計遺忘因子λ2=0.85，其它參數不變。參數估計過程中的發動機輸出扭矩、車速和加速度如圖7所示。

僅基于縱向動力學模型的整車質量和路面坡度的估計結果分別如圖8和圖9所示。從圖8可看出，達到穩定狀態后整車質量的估計值m?=1.277×104kg，質量參數估計值的相對誤差仍在5%以內；從圖9可看出，坡度參數的估計值與實際值相比存在較大偏差，特別是當路面坡度角變化較快時偏差更大。基于聯合坡度估計模型的坡度估計結果如圖10所示。

綜合對比可知，獲取道路坡度角時，僅基于縱向動力學的多遺忘因子RLS算法對于坡度變化不明顯的路面適應能力較強，能夠滿足估計的精度要求，而當道路坡度變化較快時，所提出的聯合坡度估計模型能夠更好地適應路面坡度的變化，坡度估計值更精確。

5 結束語

首先基于多遺忘因子RLS算法和縱向車輛動力學對整車質量、路面縱向坡度估計識別，然后利用基于縱向動力學模型和加速度偏差坡度模型的聯合坡度估計模型對行駛中的汽車質量與路面坡度進行實時估計，并采用商用車動力學仿真標準軟件TruckSim對估計方案進行了仿真分析，結果表明：

a.在同樣的質量估計精度下，當路面坡度變化較小時，使用聯合坡度估計模型對路面坡度的估計結果與只采用縱向動力學模型的估計結果差異較小。

b.對于坡度變化較快、坡度角較大的路面，采用聯合坡度估計模型的坡度估計值更精確，即聯合坡度估計模型能夠更好地適應路面坡度的變化。

1 Kim D,Choi S B,Oh J.Integrated Vehicle Mass Estimation Using Longitudinal and Roll Dynamics.Control Automation and Systems(ICCAS),2012 12th International Conference on,17-21 Oct.2012:862～867.

2 林棻,黃超,王偉.基于串行RLS的汽車雙參數聯合辨識.華南理工大學學報,2012,40（12）:105～109.

3 馮源,余卓平,熊璐.基于分段遞推最小二乘估計的汽車質量辨識試驗.同濟大學學報,2012,40（11）:1691～1697.

4 Pence B L,Fathy H K,Stein J L.Sprung Mass Estimation for off-road Vehicles Via Base-Excitation Suspension Dy?namics and Recursive Least Squares.American Control Con?ference,Hyatt Regency Riverfront,St.Louis,MO,USA, 2009:5043～5048.

5 Vahidi A,Stefanopoulou A and Peng H.Recursive Least Squares with Forgetting for Online Estimation of Vehicle Mass and Road Grade:Theory and Experiments.Vehicle Sys?tem Dynamics,2005,43（1）:31～55.

6 楊秀建，李海青，高晉，等.基于遞推最小二乘法的半掛汽車列車結構參數估計.昆明理工大學學報（自然科學版），2014,39（3）:43～49，60.

7 Paulo S R Diniz.Adaptive Filtering Algorithms and Practi?cal Implementation(Third Edition).Springer,New York, 2008.

8 Vahidi A,Druzhinina M and Stefanopoulou A.Simultaneous Mass and Time-Varying Grade Estimation for Heavy-Duty Vehicles.Proceedings of the American Control Conference, Denver.Colorado June 4-6,2003:4951～4956.

9 羅禹貢.一種車輛行駛過程中路面坡度的實時估計方法.中國專利:201210177067.3,2012-05-31.

（責任編輯文 楫）

修改稿收到日期為2015年4月22日。

Research on Co-estimation Method of Mass and Grade for Heavy Vehicles

Li Haiqing,Yang Xiujian,Chen Shuqiao,Gao Jin
（Kunming University of Science and Technology）

This paper focuses on the issue of mass and grade estimation algorithms for the heavy vehicles using the longitudinal dynamics and acceleration deviation gradient model based on recursive least square(RLS)with multiple forgetting factors algorithm.The proposed parameter estimation model is established based on Matlab/Simulink.A nonlinear heavy vehicle simulation model is established based on TruckSim,and this estimation method is verified by dynamic simulation of fixed gradient road and sine sweep frequency road surface.The results reveal that the road estimation using the longitudinal dynamics and acceleration deviation gradient model can well track the variation of road compared with the scheme with longitudinal dynamics only in the sine sweep gradient condition.

Truck，Mass，Road grade，Co-estimation method

載貨汽車 質量 路面坡度 聯合估計方法

U461

A

1000-3703（2015）08-0054-05

國家自然科學基金資助（編號:51005109，51465023）；云南省應用基礎研究資助項目（編號:2010ZC029）。