考慮修理結構的艦船部署能力仿真

李宣池，胡俊波，張志華

考慮修理結構的艦船部署能力仿真

李宣池，胡俊波，張志華

海軍工程大學理學院，湖北武漢430033

海上環境日益復雜，不僅要關心單艘艦船的部署能力，更要關心多艘艦船可同時部署的能力，以滿足不同軍事任務的用船需求。針對多艘同型艦船的部署能力問題，分析艦船入役時機、計劃修理間隔期及修期控制等因素對同型艦船部署能力的影響，并從軍事需求出發，提出多艘同型艦船部署能力的度量指標體系。在此基礎上，建立多艘同型艦船部署能力的數學模型，給出同型艦船部署能力的仿真算法，較好地解決了同型艦船部署能力計算困難的問題。最后，通過仿真分析發現，艦船入役時機、計劃修理間隔期及修期控制對同型艦船的部署能力具有較大影響，尤其是隨著艦船計劃修理間隔期的延長，其部署能力呈S形增加，對優化艦船修理結構，提高同型艦船部署能力，降低艦船維修保障費用具有重要意義。

艦船；部署能力；修理結構；仿真分析

期刊網址：www.ship-research.com

引用格式：李宣池，胡俊波，張志華.考慮修理結構的艦船部署能力仿真［J］.中國艦船研究，2015，10（5）：123-128.

LIXuanchi，HU Junbo，ZHANG Zhihua.Simulation analysis ofwarship dep loy ability withmaintenance structures involved［J］.Chinese Journalof Ship Research，2015，10（5）：123-128.

0　引言

艦船是一種大型的復雜海上作戰平臺，為充分發揮其作戰效能，需要在入役初期根據艦船所承擔的使命任務與裝備修理需求合理編排艦船的修理結構，確定塢修、小修、中修等不同修理類別的修理時機，從而合理安排其全壽命周期內的各種修理活動。不僅如此，隨著海上環境的日益復雜和軍事任務的多樣化，人們還關心多艘艦船可同時部署的能力，以保持多艘艦船處于可隨時執行作戰任務的狀態，最大限度地滿足不同軍事任務的用船需求。

艦船部署能力與其修理結構密切相關。傳統的艦船修理結構［1-2］是在考慮主要艦船裝備修理需求的基礎上，確定塢修、小修、中修的修理間隔期與計劃修理活動的持續時間（即修期）。這種艦船修理結構編排方法針對的主要是單艘艦船，基本不考慮與其他同型艦船在作戰部署與修理活動安排上的協調性，容易造成艦船計劃修理活動與軍事用船需求的不匹配，甚至還會出現某些時段無船可用的現象［2-3］。為有效解決艦船計劃修理活動與軍事用船需求的匹配問題，近年來，國內、外學者針對艦船修理結構的編排方法進行了大量研究［2-5］。張耀輝等［5-7］在艦船修理級別、修理時間與修理間隔期等方面進行了優化調整，以便更加準確地預測裝備修理需求，有效控制艦船各類計劃修理類別的修期，但沒有考慮艦船使用需求對艦船修理結構的影響。美海軍自2003年開始實施艦隊反應計劃以來，對艦船修理結構的編排方法進行了大量研究，尤其是針對美軍航母編隊維修問題，提出了集劃分模型［1-2，8］和二層網絡流模型［9］等編隊修理計劃的編排方法，有效延長了編隊的修理間隔期，提高了艦船部署時間。朱曉軍等［10］分析了編隊使用需求對單艦修理結構制定的影響，通過時間序列法對艦船修理結構進行優化研究，建立了編隊條件下艦船修理結構的優化模型，在編隊所屬艦船相對固定的情況下，對提高編隊在航率具有重要意義。

本文將針對多艘同型艦船部署能力問題，在分析艦船入役時機、計劃修理間隔期及修期控制等因素對同型艦船部署能力影響的基礎上，從軍事需求出發，提出多艘同型艦船部署能力的度量指標體系。針對軍事用船特點，建立至少1艘在航率、至少2艘在航率及至少k艘在航率（以下簡稱k艘在航率）的數學模型，客觀反映多艘同型艦船滿足不同軍事任務的能力。同時，為方便同型艦船部署能力指標的計算，研究k艘在航率的仿真算法，以較好地解決同型艦船部署能力指標計算困難的問題。最后，通過仿真分析艦船入役時機、計劃修理間隔期及修期控制對同型艦船部署能力的影響。

1　同型艦船部署能力度量指標及影響分析

1.1艦船部署能力度量指標

同型艦船部署能力是指某型艦船處于隨時執行戰備任務狀態的數量，以滿足不同軍事需求。當同型艦船只有1艘時，其部署能力實際上是該艦船全壽命周期內的在航總時間與艦船服役時間之比，也就是通常所指的艦船在航率。對于多艘同型艦船而言，其部署能力是指在同型艦船的共同服役時間（即服役穩態期）內，至少有1艘艦船可部署能力、至少有2艘艦船可部署能力，以及至少有k艘艦船可部署能力等，以滿足不同戰備任務的用船需求。其中，至少有1艘可部署能力是該型艦船隨時可執行一項軍事任務的可能性，至少有k艘可同時部署能力是該型艦船可同時執行k項軍事任務的可能性。在實際中，至少有k艘艦船可部署能力通常用至少有k艘艦船在航率（以下簡稱“k艘艦船在航率”）來表示，即在n艘同型艦船的服役穩態期內，保持至少有k艘艦船同時在航的時間與穩態期時間之比。

1.2同型艦船部署能力的影響因素分析

在艦船全壽命周期內，其一般處于在航和修理2種狀態。其中修理活動包括在航期間的臨時修理和計劃修理。由于臨時修理主要是針對個別艦船裝備的修理活動，故修理持續時間較短（臨時修理中，如出現嚴重故障，由于其發生的概率較小且產生機理較為復雜，故本文暫不予考慮）。從這個意義上來看，影響同型艦船部署能力的最主要因素包括計劃修理間隔期、計劃修理持續時間（計劃修期）和艦船入役時機等。

1）計劃修理間隔期對部署能力的影響分析。計劃修理間隔期是指一艘艦船2次計劃修理之間的在航時間。由單艘艦船在航率定義可以看出，傳統意義上的艦船在航率隨計劃修理間隔期的延長線性增加，但對于多艘同型艦船的部署能力，隨著計劃修理間隔期的延長，盡管k（k=1，2，…，n）艘在航率是增加的，但由于各艘艦船的計劃修理時機會出現交叉現象，使得k艘在航率與計劃修理間隔期呈現出非線性現象。由下文第4節的實例分析將可以看出，k艘在航率與計劃修理間隔期之間呈S形增加。

2）計劃修期對部署能力的影響分析。對單艘艦船而言，艦船計劃修期越長，其在航率便越小。由于艦船計劃修理活動涉及范圍大、持續時間長，為有效控制計劃修期，需要合理安排、交叉實施各種修理活動。從這個意義上看，計劃修理活動具有很大的隨機性，具體表現為艦船塢修、小修、中修的修期是一個隨機變量。設 X1，X2，X3分別表示艦船塢修、小修、中修的修期，通常認為其是服從正態分布的隨機變量。

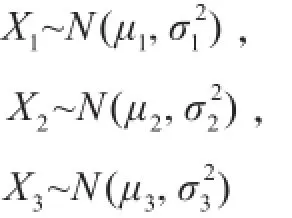
其中：μ1，μ2，μ3分別為艦船塢修、小修和中修的平均修期；σ1，σ2，σ3分別為塢修、小修和中修持續時間的標準差，反映各類計劃修理活動持續時間的波動。各類計劃修理活動的安排越周密，σ1，σ2，σ3就越小，特殊地，當 σ1=σ2=σ3=0時，說明塢修、小修和中修活動是完全按照預定的修理計劃實施各項修理任務。

3）艦船入役時機對部署能力的影響分析。對多艘同型艦船而言，由于其修理結構是相同的，因此，為保持隨時有多艘艦船可以部署，必須交錯安排每艘艦船的計劃修理活動。顯然，在艦船修理結構確定的情況下，艦船不同的入役時機對交錯實施艦船計劃修理活動具有很大的影響，甚至會出現無船可用的現象。

2　艦船部署能力數學模型

2.1單艦全壽命周期狀態的數學描述

以某型艦船為例，在全壽命周期內的修理結構為：入役—塢修—小修—塢修—中修—……—塢修—退役。為方便起見，通過矩陣MC來表達艦船修理結構，si為艦船所處的狀態，ti為艦船處于si狀態的持續時間，如t2為艦船處于狀態s2（小修）下的持續時間。

對單艘艦船而言，根據周期修理結構，si∈U，U表示艦船在服役期內所處的幾種狀態：

2.2同型艦船狀態數學描述

對于同型艦船而言，同樣可以利用矩陣方法描述各艘艦船在服役穩態期內的各種狀態。若某型艦船共有n艘，按照入役的先后順序進行排列，可以得到同型艦船的狀態矩陣：

同型艦船的狀態矩陣F_MC有關符號說明：

1）m表示第1艘艦船在穩態期內所經歷狀態的個數；m'表示第n艘艦船入役時所有同型艦船所處的狀態。

2）tij表示第i艘艦船第 j個狀態的持續時間（i=1，…，n；j=1，…，m）。例如，t11表示第1艘艦船入役后所處第1個狀態（部署狀態）的持續時間，t12表示第1艘艦船首次進行塢修的持續時間。由于第n艘艦船是在第1艘艦船處于第m'個狀態時才入列，因此，tn1=…=tnm'-1=0，tnm為第1艘艦船退役時第n艘艦船所處的狀態。

3）由于第n艘艦船是在第1艘艦船處于第m'個狀態時才入列，因此，n艘同型艦船的服役穩態期實際上是第n艘艦船入役時間到第1艘艦船退役時間，為同時服役時間。因此，服役穩態期T可表示為

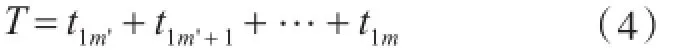
2.3艦船可部署能力數學模型

為有效提高同型艦船部署能力，需合理安排多艘同型艦船的修理活動，以便最大限度地滿足軍事需求。根據同型艦船部署能力定義，本節將建立k（k=1，…，n）艘艦船在航率的數學模型，并給出其計算方法。

1）1艘艦船在航率的數學模型。

對于n艘艦船而言，其第i艘艦船在任意時刻t所處的狀態可表示為

當 fi（t）=1（i=1，2，…，n）時，表示第i艘艦船在時刻t處于可部署狀態；當fi（t）=0（i=1，2，…，n）時，表示第i艘艦船在時刻t處于修理狀態。則

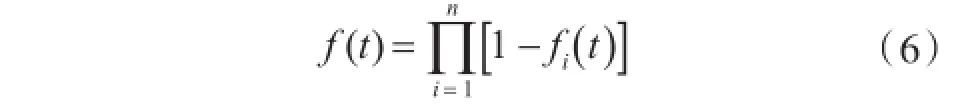
是一個只取0或1的示性函數。當 f（t）=0時，表示在時刻t至少有1艘艦船處于可部署狀態；當f（t）=1時，表示n艘艦船在時刻t同時處于在修狀態。由此可得，n艘同時在修的總時間Y1為

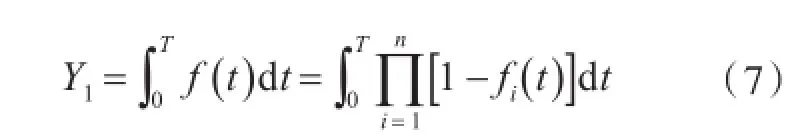
顯然，Y1是一個隨機變量，其數學期望為n艘同型艦船同時處于在修的平均時間，即

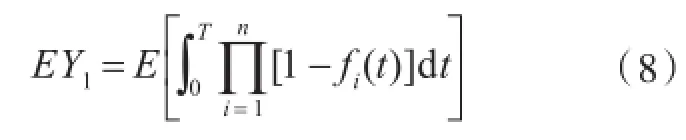
因此，1艘在航率P1可表示為

2）k艘艦船在航率的數學模型。

為獲得k艘在航率，需要計算至少有k艘艦船同時在航的總時間。由式（5）可知，恰好有i（n-k＜i≤n）艘艦船在時刻t同時處于在修的狀態可表示為

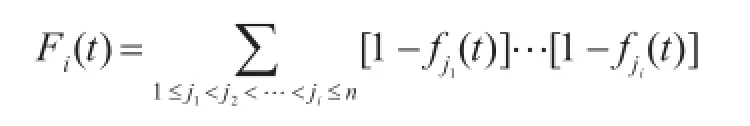
因此，至少有n-k+1艘艦船在時刻t同時處于在修的總時間為

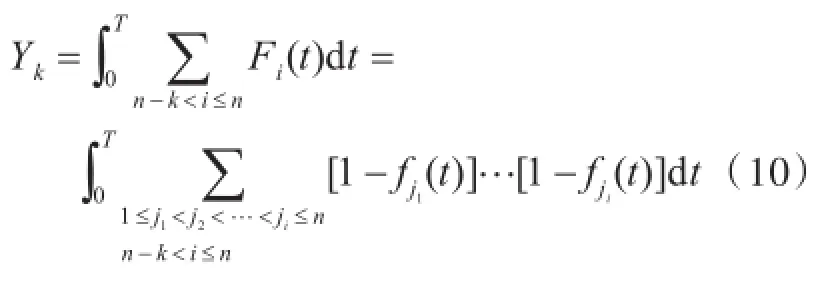
顯然，Yk是一個隨機變量，其數學期望為至少有n-k+1艘艦船同時在修的平均時間，即

從而可得到k艘在航率為

3　部署能力的仿真算法

由于各艘艦船在某時刻是否處于在航狀態具有隨機性，因此，給同型艦船部署能力的計算造成了很大困難，所以，本節將建立同型艦船部署能力的仿真模型，給出同型艦船部署能力的仿真算法。具體仿真過程如下。

1）確定n艘同型艦船的入役時間。

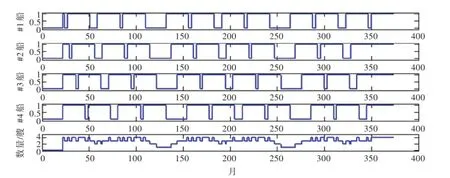
圖1　穩態期內艦船狀態情況仿真Fig.1　Simulation results of the ships in steady-state

2）隨機產生修理間隔時間。在艦船實際使用過程中，由于執行任務的影響，常常會造成艦船等級修理間隔時間為隨機變量。假定等級修理間隔時間服從均值為 μ0、方差為的正態分布，則可以隨機產生艦船在2次等級修理之間的在航時間。例如，對于第1艘艦船，利用正態分布N（μ0，σ02）可以隨機生成m+1/2隨機數，其中第1個隨機數即為第1艘艦船入役到首次塢修的在航時間，記為t11；第2個隨機數即為第1次塢修到第1次小修之間的在航時間，記為t13。

3）隨機產生修理持續時間。按照塢修、小修、中修持續時間服從的分布函數，分別產生塢修、小修、中修的持續時間，從而可以獲得n艘同型艦船結構矩陣F_MC。

4）利用結構矩陣F_MC和式（4）計算得到服役穩態期T。

5）利用結構矩陣F_M C和式（7），就可以得到至少有1艘艦船在航的總時間Y1，從而由式（8）得到至少有1艘可部署能力為P1=Y1/T。

6）類似地，利用式（11）和式（12）可以得到至少有k艘艦船可部署能力為Pk。

7）將上述步驟2）～6）重復進行1 000次仿真，并對每次得到的1艘艦船可部署能力、k艘艦船可部署能力進行平均。

4　實例分析

現有某型艦船4艘，艦船全壽命周期為374月，其修理結構為：入役—塢修—小修—塢修—中修—塢修—小修—塢修—中修—塢修—小修—塢修—退役。其中塢修修期為3個月，小修修期為8個月，中修修期為22個月，計劃修理間隔期為24個月。同時假設4艘艦船先后入役的時間間隔為5個月、7個月和10個月。根據上述假設，對各艘艦船在穩態期內所處狀態進行仿真（圖1，其中共同服役時間以第4艘艦船入役的時間為起點，之前4艘艦船所處狀態不考慮，統一記為0），并可以統計得到同型艦船在航率。

4.1艦船入役時機對部署能力影響分析

在同型艦船中，每艘艦船的入役時間不同，對艦船部署能力的影響如表1所示。以第1艘艦船入役時間為基準，當第2、第3、第4艘艦船入役時間間隔分別相差2，4，3個月時，1艘艦船在航率為0.963 0，3艘艦船在航率為0.774 9，4艘艦船在航率為0.552 7。而當第2、第3、第4艘艦船入役時間間隔分別相差4，8，6個月時，1艘艦船在航率為0.988 3，3艘在航率為0.842 1，4艘在航率為0.394 8。顯然，最后1艘艦船入役的時間與第1艘艦船入役時間間隔越小，就越容易造成同型艦船同用同修的情況，4艘同時在航的概率就越大。

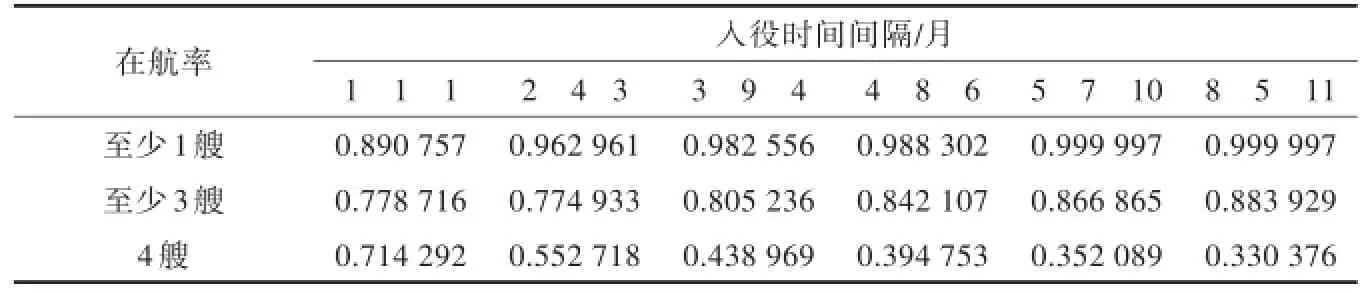
表1　不同入役時間間隔對艦船在航率的影響Tab.1　In fluences of different service tim e intervals to rate of sailing

4.2計劃修理間隔期對部署能力影響分析

在給定4艘艦船入役時間間隔分別為5，7，10個月的情況下，將計劃修理間隔期從16個月逐步增加到30個月，仿真同型艦船的部署能力（圖2）。仿真發現：當修理間隔期從16個月逐步增加到30個月時，至少有1艘艦船的在航率接近為1；至少有2艘艦船和至少有3艘艦船的在航率呈S形增長趨勢，并且在20～22個月之間出現增長拐點。即在計劃修理間隔期小于20個月時，至少有2艘艦船、至少有3艘艦船的在航率快速增加；在計劃修理間隔期大于20個月時，至少有2艘艦船、至少有3艘艦船的在航率增加緩慢。由此可見，延長計劃修理間隔期可以提高同型艦船部署能力，但過于增大計劃修理間隔期會造成在航期間裝備臨時修理任務量的增大，同時對提高同型艦船的部署能力也十分有限。

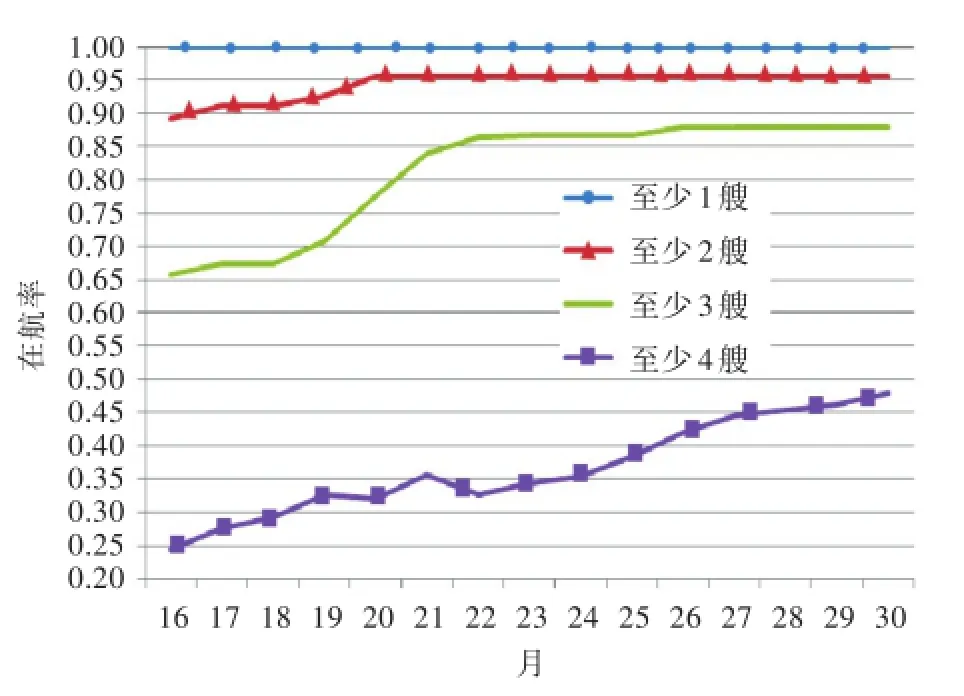
圖2　延長修理間隔期對在航率的影響Fig.2　Influence ofextending the repairing intervals to the rate ofsailing

4.3計劃修期對部署能力影響分析

艦船計劃修理持續時間（修期）的波動與計劃修理活動的管理密切相關。為反映計劃修期的波動對艦船部署能力的影響，給定艦船修理間隔期為24個月，對于不同的計劃修理類別，同時改變各類計劃修理持續時間的方差進行仿真（圖3）。隨著修期方差的增大，同型艦船在航率隨之降低，尤其對至少3艘、至少4艘在航率的變化較為明顯。因此，為有效提高同型艦船部署能力，需要科學制定修理計劃，嚴格控制修理活動，以便盡可能減小誤差。

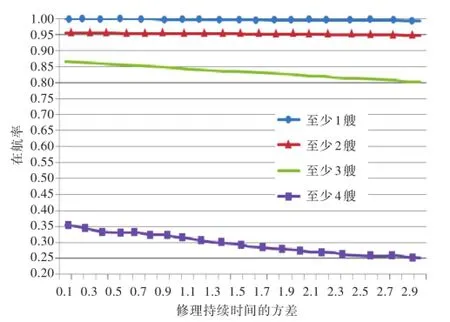
圖3　改變修理持續時間的方差對在航率的影響Fig.3　The influence of changing repairing time to the rate ofsailing

5　結語

針對同型艦船部署能力的問題，本文首先研究影響艦船部署能力的主要因素，給出了不同軍事用船需求下艦船部署能力的數學模型。由于模型計算復雜，因此采用的是實例仿真方法。計算結果表明：在實際使用中，合理編排艦船修理結構，科學組織維修保障活動，嚴格執行各項任務計劃，能夠最大限度地提高艦船部署能力，以應對瞬息萬變的海上戰場。

［1］ ROLAND JY，JOHN F S，JAMESG K.Aircraft carrier maintenance cycles and their effects［R］.Santa Monica：RAND，2008.

［2］ROLANDLY J Y，RAJ R，JESSIE R.Impacts of the fleet response p lan on surface combatantmaintenance［R］.Santa Monica：RAND，2006.

［3］HALL M.The impact of long-term aircraft carrier maintenance scheduling on the fleet readiness p lan［D］.California：Naval Postgraduate School，2004.

［4］ BROWN R L，LAWPHONGPANICH S，SCHRADY D，et al.Forward engagement requirements for US naval forces：new analytical approaches［R］.Washington，DC：Deputy Chief ofNaval Operations，1997.

［5］張耀輝，郭金茂，單志偉，等.裝備預防性維修的維修級別邏輯決策分析方法［J］.裝甲兵工程學院學報，2008，22（5）：40-44.

ZHANG Yaohui，GUO Jinmao，SHAN Zhiwei，et al. Maintenance level logic decision analysis method of preventivemaintenance［J］.Journal of Academy of Armored Force Engineering，2008，22（5）：40-44.

［6］ 程志君，郭波.連續劣化系統的最佳檢測與維修策略分析［J］.系統工程與電子技術，2008，30（1）：193-196.

CHENG Zhijun，GUO Bo.Analysis of optimal inspection and maintenance policy for continuous deteriorating system［J］.Systems Engineering and Electronics，2008，30（1）：193-196.

［7］ 何春雨，金家善，孫豐瑞.基于LINGO軟件的艦船裝備修理級別優化分析［J］.上海交通大學學報，2011，45（1）：78-82.

HE Chunyu，JIN Jiashan，SUN Fengrui.Optim ization model of ship's equipment LORA based on LINGO［J］. Journal of Shanghai Jiaotong University，2011，45（1）：78-82.

［8］ YARDLEY R J，KALLIMANIJG.A methodolgy for estimating the effect of aircraft carrier operational cycles on the maintenance industrial base［R］.Santa Monica：RAND，2007.

［9］YARDLEY R J，KALLIMANI JG.Increasing aircraft carrier forward presence：changing the length of the maintenance cycle［R］.Santa Monica：RAND，2008.

［10］朱曉軍，張濤，彭飛，等.基于編隊時間序列的艦船修理結構模型［J］.系統工程與電子技術，2012，34（11）：2285-2289.

ZHU Xiaojun，ZHANG Tao，PENG Fei，et al.Model ofmaintenance structure of ship based on time series of fleet［J］.Systems Engineering and Electronics，2012，34（11）：2285-2289.

［責任編輯：喻菁］

Sim u lation analysis ofwarship dep loy ability w ithm aintenance structures involved

LIXuanchi，HU Junbo，ZHANGZhihua
College of Science，Naval University of Engineering，Wuhan 430033，China

Asmarine environment becomes increasingly complex，the deployment of warships in different military tasks，including both singlewarship deployment aswellasmulti-warship coordination，isoften discussed.This paper analyzes themain factors that influence the deploy ability ofwarships of the same type when the warship comes into service，plans repairing interval，schedules control and etc.Based on the analysis，themeasurement indicators for concurrent dep loy ability of identicalwarships are constructed，and the correspondingmodel and the simulation algorithm is provided.The proposed approach is seen to be a good solution to the difficulties in calculating concurrent deploy ability.Finally，the simulation results suggest thatall the factors are of vital significance to the deploy ability；particularly，as themaintenance interval increases，the deploy ability shows S-shape growth.In brief，this app roach p lays a significant role for optim izing maintenance structures，promoting the deploy ability of identical warships and reducing the maintenance cost.

warship；dep loy ability；maintenance structure；simulation analysis

U674.7

ADOI：10.3969/j.issn.1673-3185.2015.05.020

2015-01-04網絡出版時間：2015-10-8 10∶43

李宣池（通信作者），男，1990年生，碩士生。研究方向：海軍裝備效能評估與保障優化。E-mail：309904546@qq.com

張志華，男，1965年生，博士，教授。研究方向：武器系統保障工程和可靠性工程

網絡出版地址：http∶//www.cnki.net/kcms/detail/42.1755.TJ.20151008.1043.004.htm l