混凝土濕度場反演算法對比分析

□馮曉波(南水北調工程建設監管中心)

0 引言

混凝土水分減少導致干縮開裂，相關研究已開展較多，牛焱洲[1]采用有限元法，根據混凝土Fick擴散定律，求出自由干縮應力和濕度分布，Bazant.Z.P和CEB-FIP（90）推薦了混凝土濕度場的非線性濕度擴散系數模型，也是現用干縮模擬的常用模型，利用遺傳算法來求解混凝土濕度場特征參數[2]。鑒于濕度特性參數的測量困難，很難進行干縮計算或簡單的估算。針對此問題，在參考文獻[2]的基礎上采用遺傳算法和微粒群算法來反演濕度場特征參數，并對反分析方法的精度和適用性進行對比分析，以期為工程設計提供理論依據。

1 計算原理與方法

1.1 濕度場計算

在混凝土中一般認為水分遷移符合Fick定律，其微分方程可以表示為：

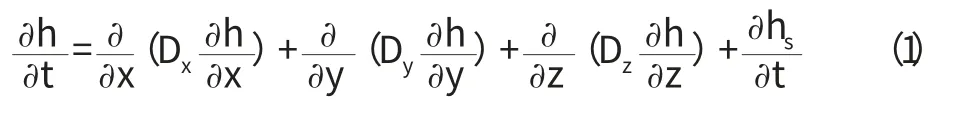
相應的初始條件為：

在與空氣接觸的邊界上，邊界條件為：

式中，h為相對濕度，Dx,Dy,Dz是濕度擴散系數，表示為D（h），hs為絕濕環境下水泥水化時消耗濕度，a，b是參數，隨水泥品種，比表面積等不同。h0（x,y,z）為已知的相對濕度；β 為表面濕度轉移系數；ha為空氣的相對濕度。

1.2 反分析基本理論[4，5]

在混凝土濕度場特征參數反演分析過程中，通常采用最小二乘法估計反演參數的適應值，即將實測濕度和有限元計算的濕度差值的平方和作為參數反演的目標函數，來尋求與工程實際條件下混凝土結構濕度變化過程較為接近計算參數，即

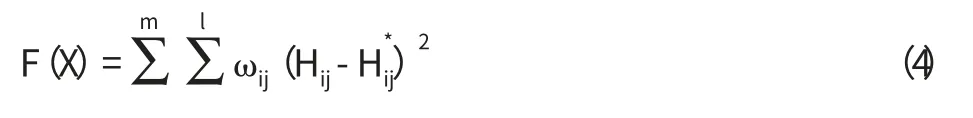
式中，X表示反演參數變量；ωij表示在第j時刻第i點的加權系數；Hij表示在第j時刻第i點根據有限元計算得到的濕度值代表在第j時刻第i點實測濕度值；m為觀測點的數目；l為某測點觀測時間點數目。

在濕度場反分析過程中，需進行迭代計算，選擇各種不同的數學優化方法，如傳統的模式搜索法、單純形法、鮑威爾法等，近幾年來又出現了神經網絡法、遺傳算法、粒子群算法等新方法。

遺傳算法和微粒群算法是解決最優化問題的有效途徑和通用框架，是一種新的全局優化搜索算法，所求出的近似最優解或滿意解是人們的主要著眼點之一。本文就這兩種算法進行反分析研究以對比其合理性。

2 試驗情況

見文[3]中的水灰比0.4的中強度混凝土試塊，尺寸為10 cm×10 cm×20 cm，其中一個面散濕，其他絕濕，散濕面為10 cm×10 cm，埋設濕度探頭的A，B，C點位于散濕面中軸線上，距離散濕面3 cm，7 cm和12 cm，混凝土試塊澆注1 d后拆模，放置在水中浸泡3 d放在相對濕度50%，溫度20℃的環境中。試驗結果列于表1。

3 反演方法對比

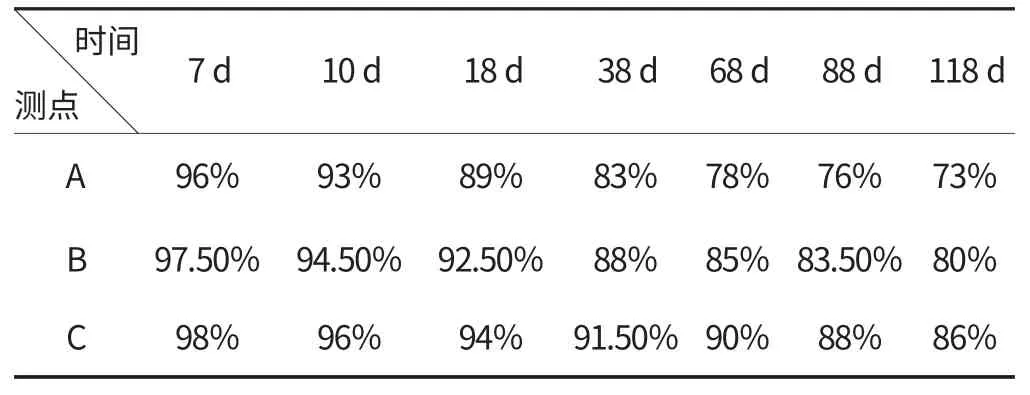
表1 實測的特征點相對濕度表

根據試驗澆注塊原型建立有限元模型，計算的節點和單元數分別是1089個和800個，在計算的過程中，暴露面按照第三類邊界條件處理。

根據實測3個點的濕度，對混凝土自干燥消耗相對濕度的hs=hs∞（1-e-aτb）中的最終消耗濕度hs∞，a和b，以及D1和β 進行了反演分析。澆筑的前三天，時間步長為0.50 d，隨后時間步長為1 d，目標優化函數取為其中i為測點號；j為觀測時刻和hij分別為實測和計算濕度值；m和n分別為測點數和測次數。

采用遺傳算法計算時取交叉概率為70%，變異概率為10%，系數α 取0.10，經過15次的迭代求解，反演辨識的混凝土的最終消耗濕度為hs∞=-0.15，濕度變化規律函數參數a＝0.05和b＝0.79；混凝土的表面濕度轉移系數β=2.88×10-4m/d，最大濕度擴散系數D1=3.84×10-5m2/d。采用粒子群算法計算時取加速因子c=2.00，經過13次的迭代求解，hs∞=-0.14，a＝0.04和b＝0.87，β=2.94×10-4m/d，D1=3.92×10-5m2/d。

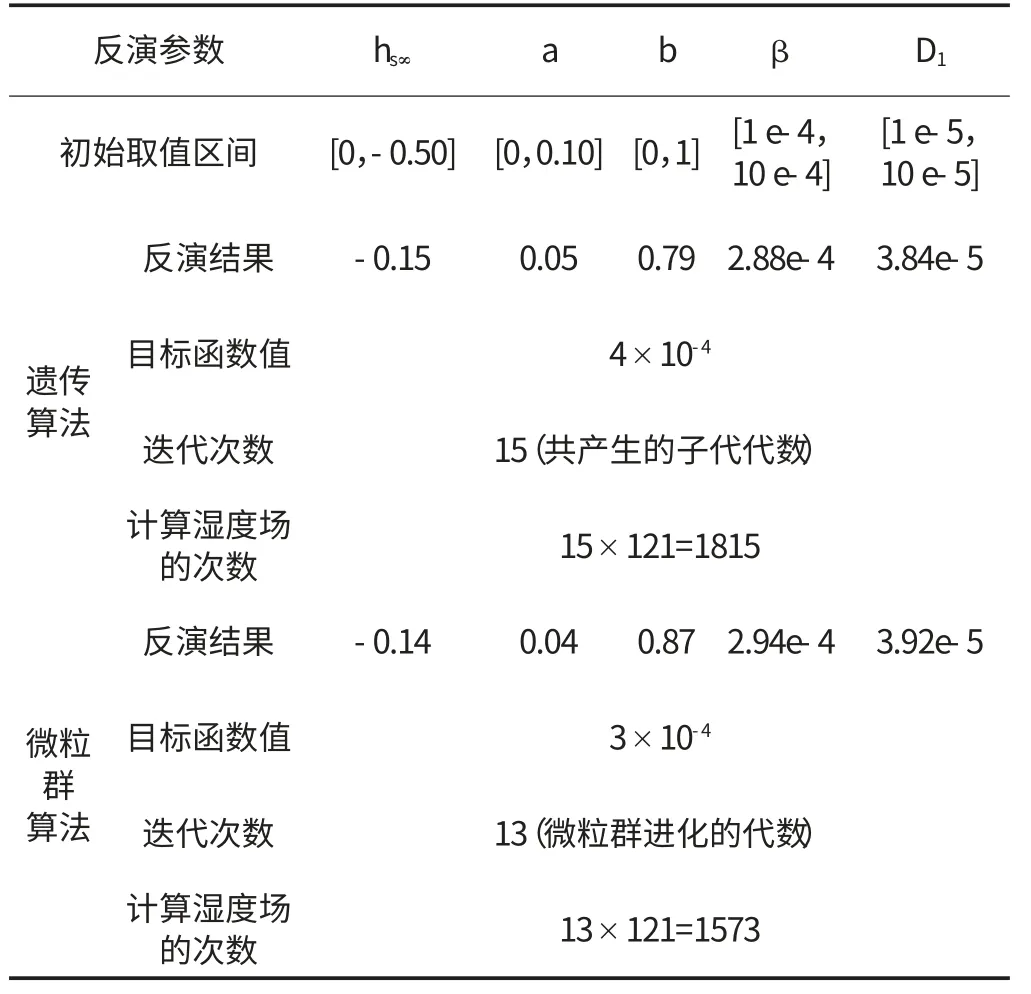
表2 兩種算法的濕度場參數反演計算結果表

對于實際工程來說，模型剖分節點和單元量大，計算時間較長，每減少一次迭代次數都會節約大量的計算時間，從這個方面來說，微粒群算法相比效率較高。而且其計算的精度也較高，本次計算過程中濕度場的計算次數為121，如果提高計算次數，可以得到更優的參數值。

微粒群算法反演出的濕度場參數計算出的特征點相對濕度歷時曲線與特征點實測相對濕度歷時曲線最貼近，幾乎重合。而遺傳算法的效果要稍差一些。通過遺傳算法反算出的各特征點相對濕度值均低于實測濕度值，但二者發展規律是一致的。

4 結語

根據室內試驗實測濕度值，利用遺傳算法和微粒群算法對混凝土試塊濕度場進行反演計算，并將計算結果和實測數據進行對比，結果表明計算結果跟實際情況相符，說明得到的參數可以反映混凝土濕度擴散規律，為實施防干縮措施提供理論依據。

遺傳算法和微粒群算法反演的濕度場和實測相比，微粒群算法計算結果相對更加精確且計算次數較少，收斂速度較快，更適合用于工程反演計算。

[1]牛焱洲，涂傳林.混凝土澆筑塊的濕度場與干縮應力[J].水力發電學報,1991(2):87-95.

[2]郭利霞，朱岳明，等.基于遺傳算法的混凝土濕度場特征參數求解及反分析[J].天津大學學報,2010,43(8):712-716.

[3]Jin-Keun Kim,Chi l-Sung Lee.Moisture diffusion of concrete considering self-desiccation at early ages[J].Cement and Concrete Research,1999,Vol.29:1921-1927.

[4]陳國良,王煦法，等.遺傳算法及其應用[M].北京：人民郵電出版社,1996：101-203.

[5]徐果明著.反演理論及其應用[M].北京:地震出版社,2003：1-5.