基于擴(kuò)散策略的實(shí)時(shí)分布式協(xié)作頻譜檢測算法

張政保 姚少林許 鑫 劉廣凱

（軍械工程學(xué)院信息工程系 石家莊 050003）

基于擴(kuò)散策略的實(shí)時(shí)分布式協(xié)作頻譜檢測算法

張政保 姚少林*許 鑫 劉廣凱

（軍械工程學(xué)院信息工程系 石家莊 050003）

針對傳統(tǒng)分布式協(xié)作頻譜檢測算法認(rèn)知用戶不能實(shí)時(shí)檢測問題，該文提出基于擴(kuò)散策略的實(shí)時(shí)分布式協(xié)作檢測算法。算法利用各個(gè)節(jié)點(diǎn)的本地代價(jià)表示全局代價(jià)，通過最小化各個(gè)節(jié)點(diǎn)的代價(jià)使得全局代價(jià)最小。采用最速下降法，利用迭代方式計(jì)算各個(gè)節(jié)點(diǎn)檢測量的最優(yōu)估計(jì)值，得出估計(jì)值的理論穩(wěn)態(tài)均值和方差，得出虛警概率、檢測概率以及檢測門限的封閉表達(dá)式。理論分析和實(shí)驗(yàn)結(jié)果表明，該算法能夠有效解決分布式網(wǎng)絡(luò)認(rèn)知節(jié)點(diǎn)的實(shí)時(shí)檢測問題，并具備快速學(xué)習(xí)和適應(yīng)環(huán)境變化的能力。當(dāng)虛警概率為0.01且檢測概率達(dá)到0.9時(shí)，平均信噪比較平均共識(shí)和非實(shí)時(shí)擴(kuò)散策略降低了約6 dB，能夠?qū)崿F(xiàn)在極低信噪比條件下的信號檢測。

認(rèn)知無線電；協(xié)作頻譜感知；分布式估計(jì)；擴(kuò)散策略；共識(shí)策略

1 引言

分布式協(xié)作頻譜檢測是較大空間范圍內(nèi)多認(rèn)知節(jié)點(diǎn)協(xié)作檢測技術(shù)。相對于集中式技術(shù)，分布式網(wǎng)絡(luò)中的單個(gè)節(jié)點(diǎn)通過和相鄰節(jié)點(diǎn)信息交換，單個(gè)節(jié)點(diǎn)進(jìn)行數(shù)據(jù)處理，解決整個(gè)網(wǎng)絡(luò)的協(xié)作問題，目標(biāo)就是通過分布式行為自適應(yīng)估計(jì)網(wǎng)絡(luò)的參數(shù)［1-3］。文獻(xiàn)［4］提出平均共識(shí)策略實(shí)現(xiàn)分布式協(xié)作，每個(gè)節(jié)點(diǎn)通過和一跳相鄰節(jié)點(diǎn)交換檢測數(shù)據(jù)，通過迭代求解，最終使每個(gè)節(jié)點(diǎn)的檢測量信息達(dá)到一致。文獻(xiàn)［5］提出一種基于信噪比加權(quán)共識(shí)協(xié)作算法，克服了平均共識(shí)算法無法體現(xiàn)認(rèn)知節(jié)點(diǎn)信噪比差異的缺陷。傳統(tǒng)分布式檢測算法將整個(gè)感知過程分為兩個(gè)過程，一是單個(gè)節(jié)點(diǎn)獲取初始檢測量信息，二是認(rèn)知節(jié)點(diǎn)通過協(xié)作策略使檢測量達(dá)到一致收斂［6］。這種數(shù)據(jù)處理方式不能實(shí)時(shí)適應(yīng)和跟蹤數(shù)據(jù)流統(tǒng)計(jì)量信息的變化，實(shí)現(xiàn)分布式網(wǎng)絡(luò)認(rèn)知節(jié)點(diǎn)的實(shí)時(shí)信號檢測。

擴(kuò)散策略能用于解決分布式估計(jì)和分布式最優(yōu)化、自適應(yīng)等問題［7-13］。擴(kuò)散策略利用各個(gè)節(jié)點(diǎn)的代價(jià)表示全局代價(jià)，利用最速下降法，迭代求解出各個(gè)節(jié)點(diǎn)的最優(yōu)值［8，9］。最大最小特征值 （Maximum-Minimum Eigenvalue， MME）檢測算法是一種經(jīng)典的盲信號檢測算法，對噪聲功率不確定性有較好的魯棒性［2，13-16］。本文將擴(kuò)散策略引入分布式網(wǎng)絡(luò)認(rèn)知節(jié)點(diǎn)的協(xié)作檢測過程，提出基于擴(kuò)散策略的分布式協(xié)作頻譜檢測算法，解決分布式網(wǎng)絡(luò)認(rèn)知節(jié)點(diǎn)的實(shí)時(shí)信號檢測問題，所有節(jié)點(diǎn)不需要中心處理單元能夠獨(dú)自做出判決。該算法將MME檢測的檢測統(tǒng)計(jì)量作為認(rèn)知節(jié)點(diǎn)的交換信息，采用擴(kuò)散策略使各認(rèn)知節(jié)點(diǎn)能夠根據(jù)相鄰節(jié)點(diǎn)的檢測量取值得到使自身代價(jià)最小的最優(yōu)的檢測量，同時(shí)各個(gè)認(rèn)知節(jié)點(diǎn)獨(dú)自做出實(shí)時(shí)判決。理論推導(dǎo)了檢測量估計(jì)值的穩(wěn)態(tài)均值和方差，得出了虛警概率、檢測概率以及檢測門限的計(jì)算公式。仿真實(shí)驗(yàn)結(jié)果表明，所提算法不僅解決了分布式網(wǎng)絡(luò)認(rèn)知節(jié)點(diǎn)對主用戶（Primary User， PU）信號的實(shí)時(shí)檢測問題，檢測量的穩(wěn)態(tài)均值性能和網(wǎng)絡(luò)均方差性能更好，檢測精度較其他分布式算法大大提高。

2 網(wǎng)絡(luò)模型及信號檢測模型

考慮一個(gè)由K個(gè)認(rèn)知節(jié)點(diǎn)構(gòu)成的分布式認(rèn)知網(wǎng)絡(luò)。它可以描述為無向圖模型 G = （V，ξ），其中節(jié)點(diǎn)集合邊集為認(rèn)知節(jié)點(diǎn)在單跳通信范圍內(nèi)的無序節(jié)點(diǎn)對，鄰集為節(jié)點(diǎn)k的單跳通信相鄰節(jié)點(diǎn)集，集合 Nk中元素的個(gè)數(shù)|Nk|為節(jié)點(diǎn)k的度。

認(rèn)知無線電網(wǎng)絡(luò)（Cognitive Radio Network，CRN）中，認(rèn)知用戶（Cognitive Users， CU）對PU信號的檢測可以看作是二元檢測模型。

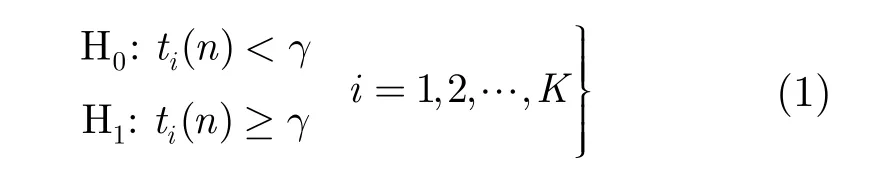
ti（n）表示認(rèn)知節(jié)點(diǎn)i在第n個(gè)感知階段的檢測量，γ表示檢測門限。認(rèn)知節(jié)點(diǎn)實(shí)時(shí)分布式協(xié)作的結(jié)果體現(xiàn)在節(jié)點(diǎn)檢測量數(shù)值的變化，各個(gè)節(jié)點(diǎn)通過與預(yù)設(shè)門限值對比，獨(dú)自做出對PU信號的檢測判決。H0表示檢測量小于門限值，PU信號不存在。H1表示檢測量大于等于門限值，PU信號存在。

3 基于擴(kuò)散策略的分布式協(xié)作檢測算法

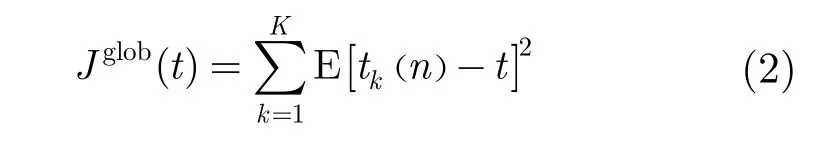
分布式協(xié)作的目的是要根據(jù)實(shí)時(shí)檢測量 t（n）得出全局期望檢測量t°的估計(jì)值t，使得全局的代價(jià)最小［8］。定義全局代價(jià)函數(shù)為K 個(gè)認(rèn)知節(jié)點(diǎn)要通過分布式行為對t°做出估計(jì)。如圖1所示，認(rèn)知節(jié)點(diǎn)k只能與其相鄰節(jié)點(diǎn)進(jìn)行信息交互，而不能獲得認(rèn)知網(wǎng)絡(luò)所有節(jié)點(diǎn)的代價(jià)信息，因此必須采用分布式策略使得單個(gè)節(jié)點(diǎn)可以與相鄰節(jié)點(diǎn)信息交換得到全局代價(jià)。

3.1 分布式擴(kuò)散最小均方估計(jì)

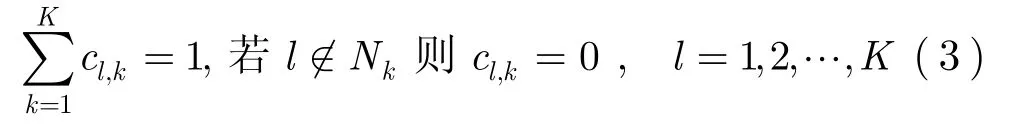
Nk表示節(jié)點(diǎn)k的鄰居節(jié)點(diǎn)集，能夠共享信息。cl，k表示節(jié)點(diǎn)k接受節(jié)點(diǎn)l信息的權(quán)重。利用系數(shù) ｛ cl，k｝，節(jié)點(diǎn)k的本地代價(jià)以及相應(yīng)的最優(yōu)解可以表示為

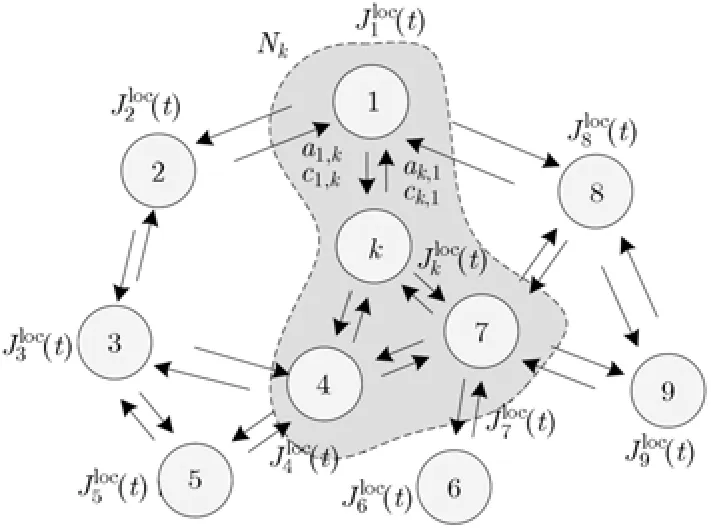
圖1 10節(jié)點(diǎn)分布式網(wǎng)絡(luò)

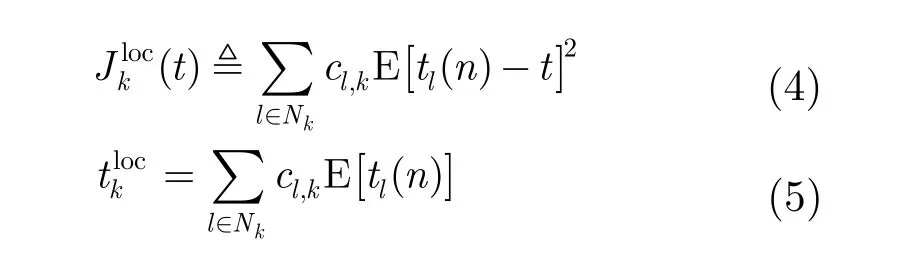
全局代價(jià)可以用節(jié)點(diǎn)k本地代價(jià)和其他節(jié)點(diǎn)本地代價(jià)函數(shù)的最優(yōu)解表示：

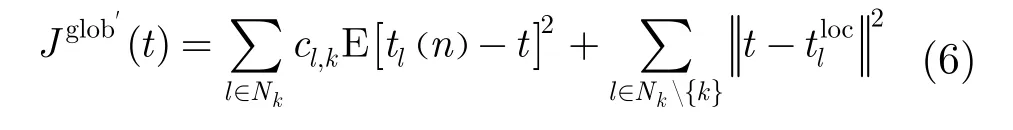
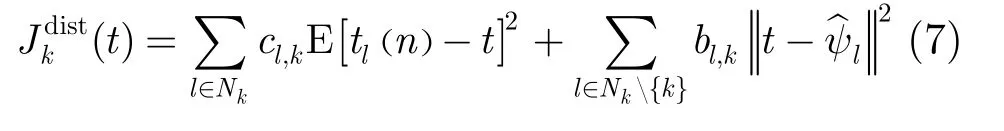
對式（7）進(jìn)行求導(dǎo)得

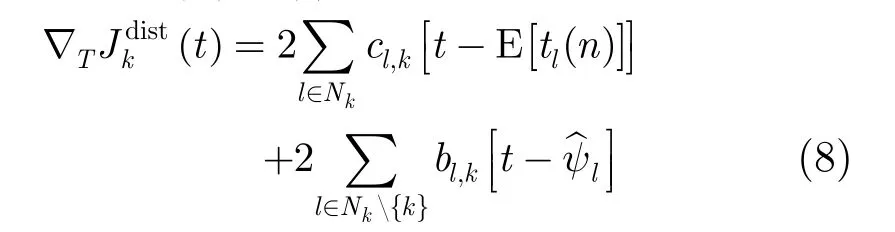
任一節(jié)點(diǎn)k可以利用最速下降法通過迭代方式得到式（7）的最優(yōu)解。迭代解的形式為

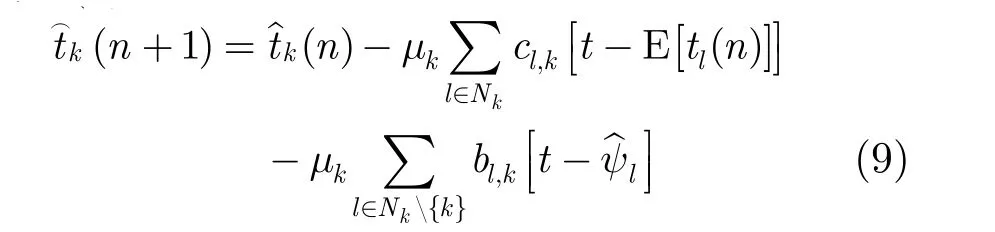
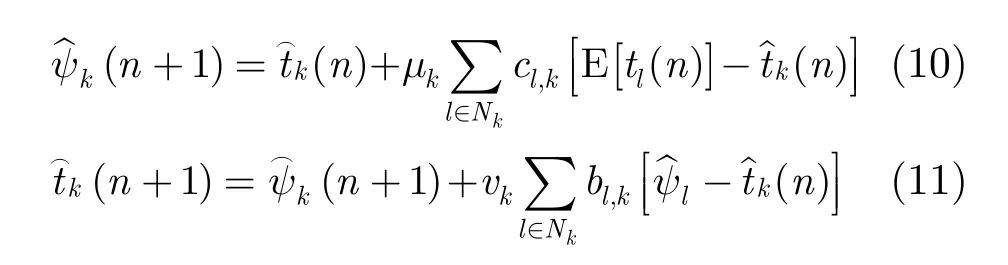
oc更好的估計(jì)，可以用k（n + 1）對式（11）中的k（n）進(jìn)行替換。

根據(jù)以上分析，式（11）可以重新表示為

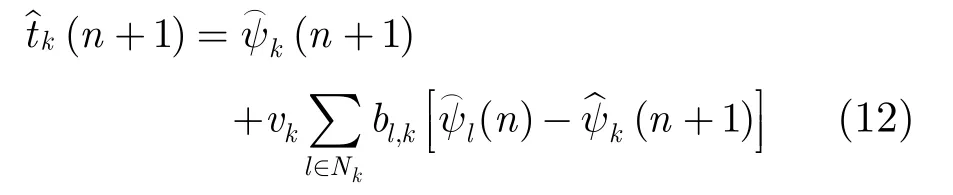
合并后可得

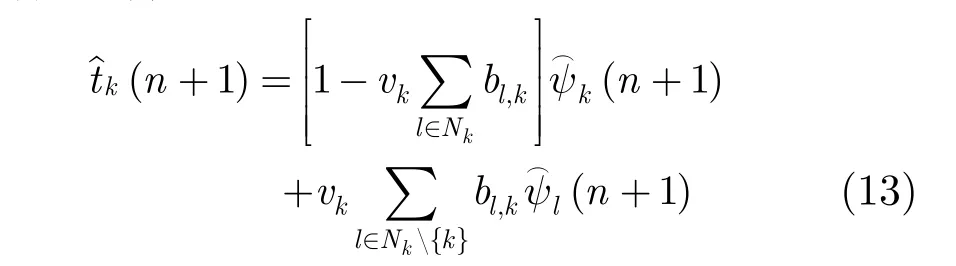
引入系數(shù) al，k，定義

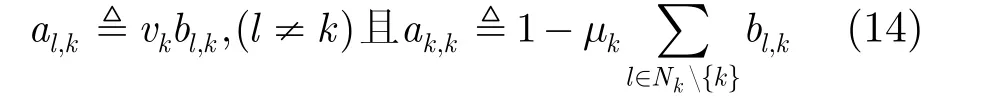
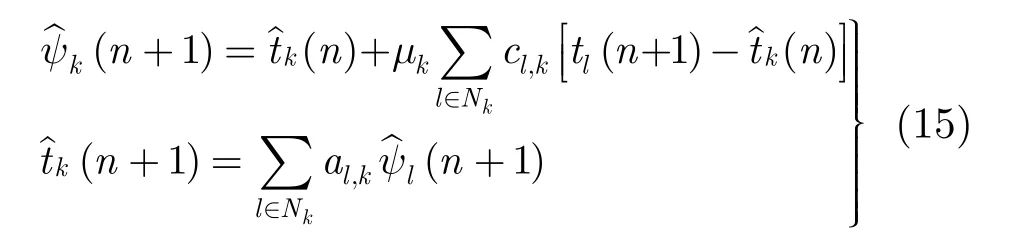
如果對調(diào)式（10）和式（11）的位置實(shí)現(xiàn)式（9），可以得出融合適應(yīng)（Combine-Then-Adapt， CTA）擴(kuò)散算法。

3.2 算法的數(shù)據(jù)處理過程及具體實(shí)現(xiàn)步驟

擴(kuò)散算法的數(shù)據(jù)處理過程如圖2所示，檢測算法的具體步驟如表1、表2所示。

ATC擴(kuò)散算法可以分為兩個(gè)過程。首先是自適應(yīng)更新過程，在n時(shí)刻，節(jié)點(diǎn)k利用自身估計(jì)值（n）和新增的相鄰節(jié)點(diǎn)檢測量信息 tl（n + 1）得到中間估計(jì)值 ψ?k（n + 1），系數(shù) cl，k決定了節(jié)點(diǎn)間檢測量信息的交換。再是合并更新過程，節(jié)點(diǎn)k的估計(jì)值k（n +1）通過對其相鄰節(jié)點(diǎn)的中間估計(jì)值（n + 1）線性合并得到，系數(shù) al，k決定了合并權(quán)重。

CTA擴(kuò)散算法也可以分為兩個(gè)過程。首先是合并更新過程，在n時(shí)刻，節(jié)點(diǎn)k通過相鄰節(jié)點(diǎn)估計(jì)值（n）線性合并得到中間估計(jì)值（n），系數(shù) cl，k決定合并權(quán)重。再是自適應(yīng)更新過程，節(jié)點(diǎn)k利用中間估計(jì)值（n）和新增的鄰居節(jié)點(diǎn)的檢測量信息tl（n + 1）得出 n +1時(shí)刻的估計(jì)值（n +1），系數(shù) al，k決定了節(jié)點(diǎn)間的信息交換過程。

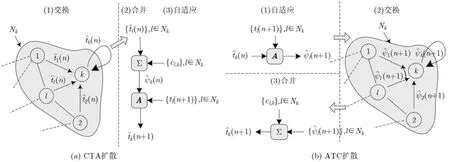
圖2 ATC擴(kuò)散和CTA擴(kuò)散策略

ATC擴(kuò)散算法和CTA擴(kuò)散算法的區(qū)別在于合并更新過程和自適應(yīng)更新過程的順序。根據(jù)表 1、表2的算法實(shí)現(xiàn)過程可以看出，ATC擴(kuò)散算法認(rèn)知節(jié)點(diǎn)信息交換需要兩次交互實(shí)現(xiàn)檢測量估計(jì)過程，先是交換再交換中間變量CTA 擴(kuò)散算法信息交換只需要一次，交換可以看出，ATC擴(kuò)散算法信息交互更加充分，能夠提高檢測精度，而CTA擴(kuò)散算法檢測量融合過程消耗能量更少，能夠提高融合效率。

表1 ATC擴(kuò)散的檢測算法流程

表2 CTA擴(kuò)散的檢測算法流程

4 性能分析

所提算法的性能分析可以分為兩部分。一是分析基于ATC擴(kuò)散策略和CTA擴(kuò)散策略的檢測量估計(jì)值的穩(wěn)態(tài)均值和方差。二是分析把MME檢測算法的檢測量作為交互信息的分布式協(xié)作檢測算法的檢測性能。

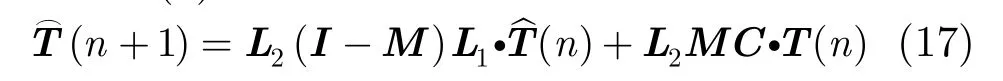
節(jié)點(diǎn)的初始估計(jì)值為T︿ （0）。對于ATC擴(kuò)散算法，我們?nèi)?L1=I，L2=A，C =A或 C =I。對于CTA擴(kuò)散算法，我們?nèi)?L1=A，L2=I，C =A或C =I。當(dāng)L1= L2= C =I時(shí)，可以表示非合作檢測量估計(jì)算法。

4.1 均值估計(jì)

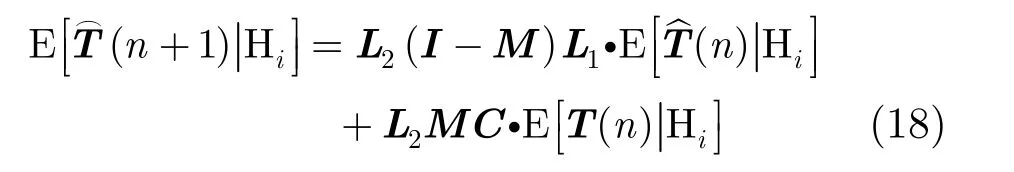
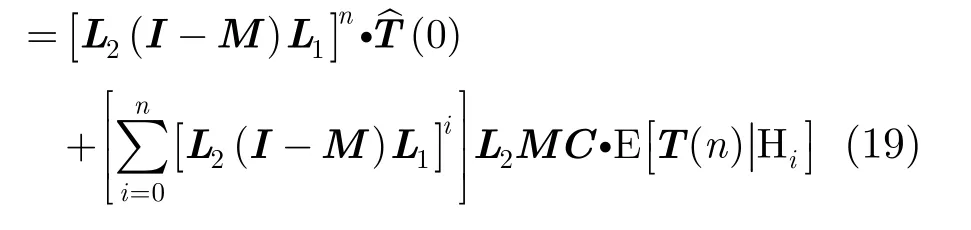
在一定范圍內(nèi)選擇 μk且保證矩陣可逆，可以使估計(jì)值收斂至穩(wěn)定狀態(tài)。可以得到穩(wěn)態(tài)時(shí)的均值為

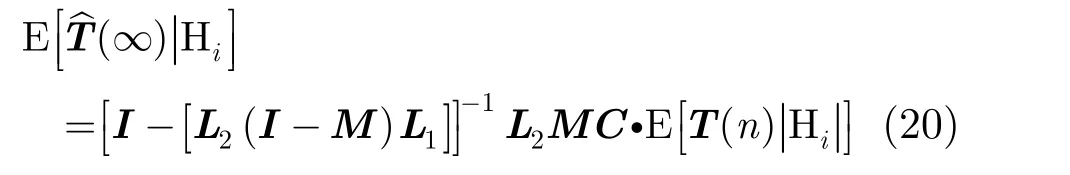
式（20）是兩種擴(kuò)散算法的通用的穩(wěn)態(tài)估計(jì)值理論表達(dá)式。

4.2 方差估計(jì)

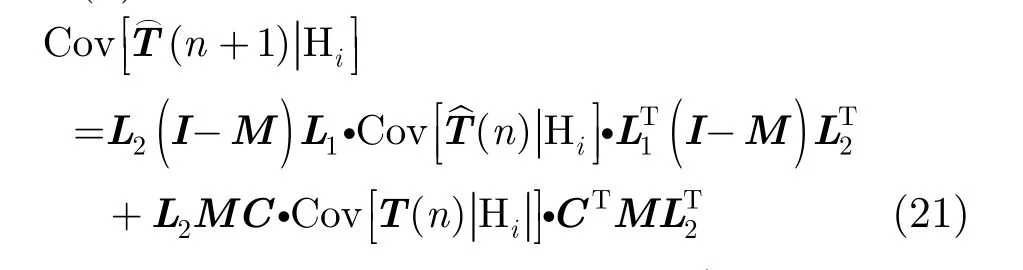
式（20）為離散時(shí)間代數(shù)黎卡提微分方程（Discrete-time Algebraic Riccati Equation， DARE）。節(jié)點(diǎn)k的穩(wěn)態(tài)方差可以根據(jù)穩(wěn)態(tài)協(xié)方差矩陣的對角線元素｛k ，k ｝得到，而為DARE的解［9］。

4.3 檢測性能分析

節(jié)點(diǎn)k在n時(shí)刻的檢測量的估計(jì)值是通過分布式擴(kuò)散算法得到的，因此檢測性能依賴檢測量的估計(jì)過程。推導(dǎo)檢測概率 Pd和虛警概率 Pfa公式需要知道 H0， H1條件下檢測量估計(jì)值（n +1）的概率密度函數(shù)（Probability Density Function， PDF）。

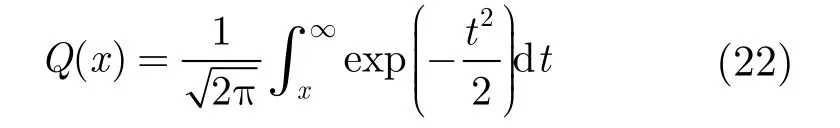
根據(jù)式（18）和式（21）可以很容易得到節(jié)點(diǎn)k的條件均值和條件方差可以根據(jù)穩(wěn)態(tài)結(jié)果得到相應(yīng)的穩(wěn)態(tài)值。我們給出近似的基于擴(kuò)散策略的分布式協(xié)作的檢測性能。在 H0條件下的檢測虛警概率為

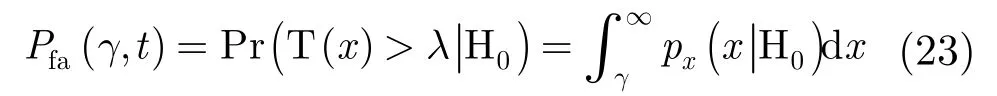
代入 H0條件下的估計(jì)均值和方差，可以得到

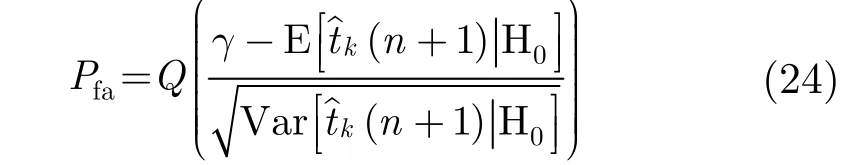
H1條件下的檢測概率為

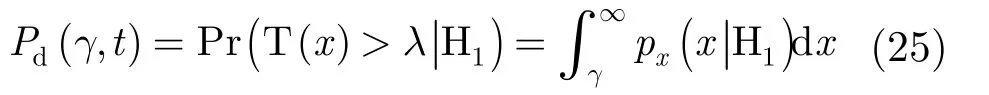
定義節(jié)點(diǎn)k的檢測概率為 Pd，k，代入 H1條件下的估計(jì)均值和方差，可以得到

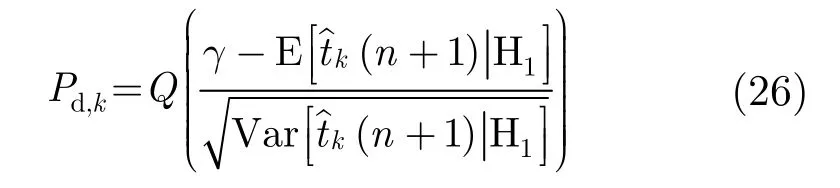
通過固定虛警概率 Pfa，根據(jù)式（23）可以得到檢測門限為

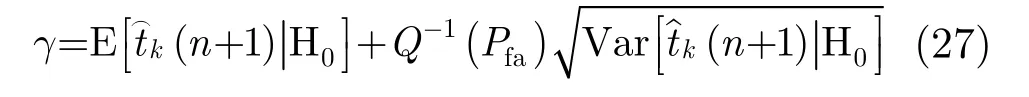
理論上每個(gè)認(rèn)知節(jié)點(diǎn)的檢測門限是相同的。計(jì)算門限要求知道 H0條件下檢測量估計(jì)值一、二階矩，這依賴算法的參數(shù)，特別是步長參數(shù)。實(shí)際過程中矩計(jì)算可以在給定步長參數(shù)和融合矩陣的前提下通過式（18）和式（21）提前計(jì)算。

5 仿真結(jié)果

仿真部分主要對基于擴(kuò)散策略的分布式檢測算法的檢測量估計(jì)性能、網(wǎng)絡(luò)中認(rèn)知節(jié)點(diǎn)的瞬時(shí)方差、穩(wěn)態(tài)條件下各節(jié)點(diǎn)的方差、算法的檢測性能進(jìn)行了Matlab仿真實(shí)驗(yàn)。仿真采用10節(jié)點(diǎn)認(rèn)知網(wǎng)絡(luò)，其拓?fù)潢P(guān)系和信噪比信息如圖3所示。仿真實(shí)驗(yàn)中，PU信號為高斯白噪聲信道下的QPSK信號，其基帶碼元速率為2 kbps，載波信號為10 kHz，數(shù)據(jù)采樣速率為50 kHz。

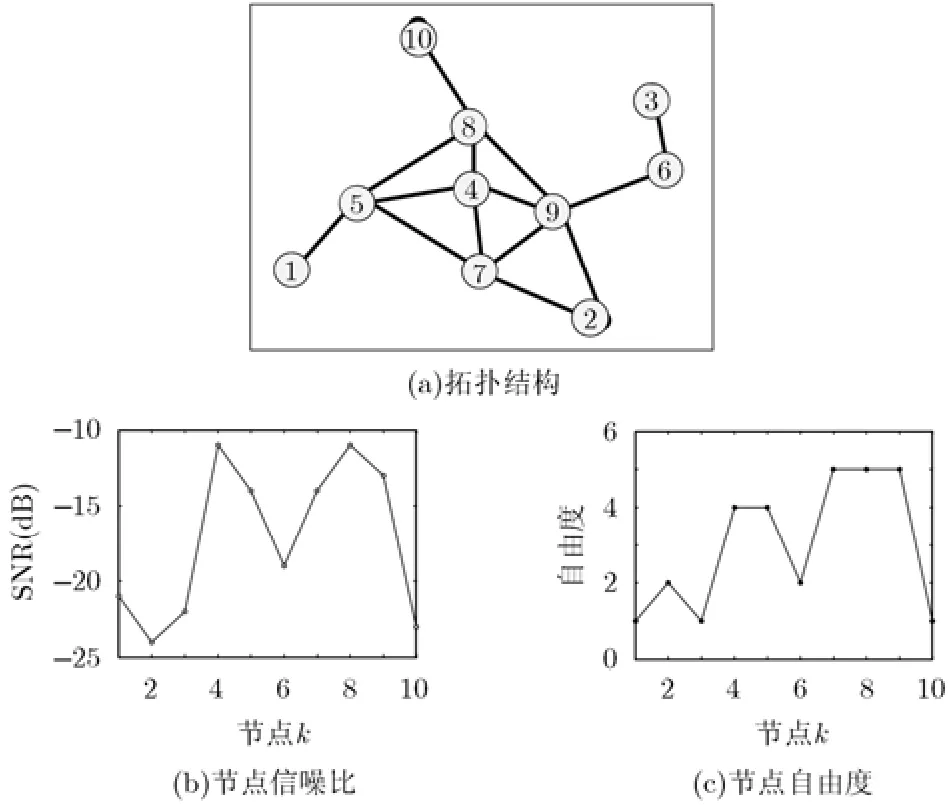
圖3 10節(jié)點(diǎn)拓?fù)渚W(wǎng)絡(luò)結(jié)構(gòu)

5.1 分布式檢測量估計(jì)性能

仿真實(shí)驗(yàn)中每個(gè)認(rèn)知節(jié)點(diǎn)對 PU信號進(jìn)行MME檢測，采樣數(shù)據(jù)長度為2000，可以得到節(jié)點(diǎn)k在n時(shí)刻的檢測量測量值k ∈ K。節(jié)點(diǎn)間分別采用平均共識(shí)策略、非實(shí)時(shí)擴(kuò)散策略、ATC擴(kuò)散策略、CTA擴(kuò)散策略協(xié)作進(jìn)行檢測量估計(jì)。按照圖2的拓?fù)浣Y(jié)構(gòu)對各認(rèn)知節(jié)點(diǎn)的檢測值進(jìn)行性協(xié)作估計(jì)。實(shí)驗(yàn)過程中PU信號在前1000個(gè)檢測時(shí)刻存在，之后1000個(gè)檢測時(shí)刻僅有噪聲信號。擴(kuò)散策略采用的步長 μk= 0.05，自適應(yīng)矩陣A和融合矩陣C根據(jù)拓?fù)浣Y(jié)構(gòu)按照相對自由度的方法取值。

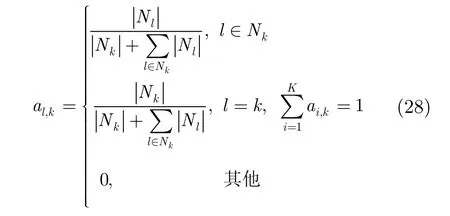
圖4是根據(jù)4種分布式策略得到的檢測量估計(jì)值曲線。可以看出，實(shí)時(shí)擴(kuò)散策略得到的檢測量估計(jì)值無論P(yáng)U信號是否存在方差都更小，ATC擴(kuò)散策略的估計(jì)值穩(wěn)定性最好。ATC策略的穩(wěn)態(tài)方差最小，檢測性能理應(yīng)最好。平均共識(shí)策略和非實(shí)時(shí)擴(kuò)散策略僅僅是對某個(gè)時(shí)刻各節(jié)點(diǎn)的檢測值進(jìn)行融合估計(jì)，而實(shí)時(shí)擴(kuò)散策略利用了歷史數(shù)據(jù)，節(jié)點(diǎn)融合了更多的檢測量信息，每個(gè)節(jié)點(diǎn)都不會(huì)因?yàn)槟骋粫r(shí)刻自身檢測值失效而出現(xiàn)估計(jì)值的劇烈變動(dòng)。從 4幅圖中可以大致看出 ATC擴(kuò)散策略所有節(jié)點(diǎn)的估計(jì)值穩(wěn)態(tài)方差最小，平均共識(shí)策略的穩(wěn)態(tài)方差最大。

實(shí)時(shí)擴(kuò)散算法的優(yōu)勢在于實(shí)時(shí)性，當(dāng)PU在有無之間切換時(shí)，能否快速學(xué)習(xí)，快速達(dá)到估計(jì)值穩(wěn)定直接影響算法性能。圖5是ATC算法的初始學(xué)習(xí)和自適應(yīng)曲線。實(shí)驗(yàn)對ATC擴(kuò)散算法在前10個(gè)時(shí)刻以及第951至第1150個(gè)時(shí)刻之間節(jié)點(diǎn)檢測量估計(jì)值進(jìn)行了細(xì)節(jié)描述。可以看出，所有節(jié)點(diǎn)的估計(jì)值在第 5個(gè)檢測時(shí)刻過后達(dá)到穩(wěn)定。第 1000個(gè)時(shí)刻PU信號不存在之后，所有節(jié)點(diǎn)能夠迅速適應(yīng)環(huán)境變化，經(jīng)過大約70個(gè)檢測時(shí)刻后，估計(jì)值達(dá)到了穩(wěn)定，按照50 kHz的采樣速率，節(jié)點(diǎn)估計(jì)值達(dá)到穩(wěn)定的時(shí)間大約為2.8 s。適應(yīng)時(shí)間主要與算法迭代步長 μk相關(guān)，迭代步長越大，認(rèn)知節(jié)點(diǎn)檢測量達(dá)到穩(wěn)定所需的時(shí)間越短，但是融合的效果變差，因此自適應(yīng)學(xué)習(xí)的速度和融合的精度之間存在折中。在實(shí)際協(xié)作檢測過程中，可以根據(jù)實(shí)際情況調(diào)整步長大小，使得在滿足認(rèn)知用戶檢測精度的條件下最大限度提高認(rèn)知節(jié)點(diǎn)對環(huán)境變化的適應(yīng)能力。

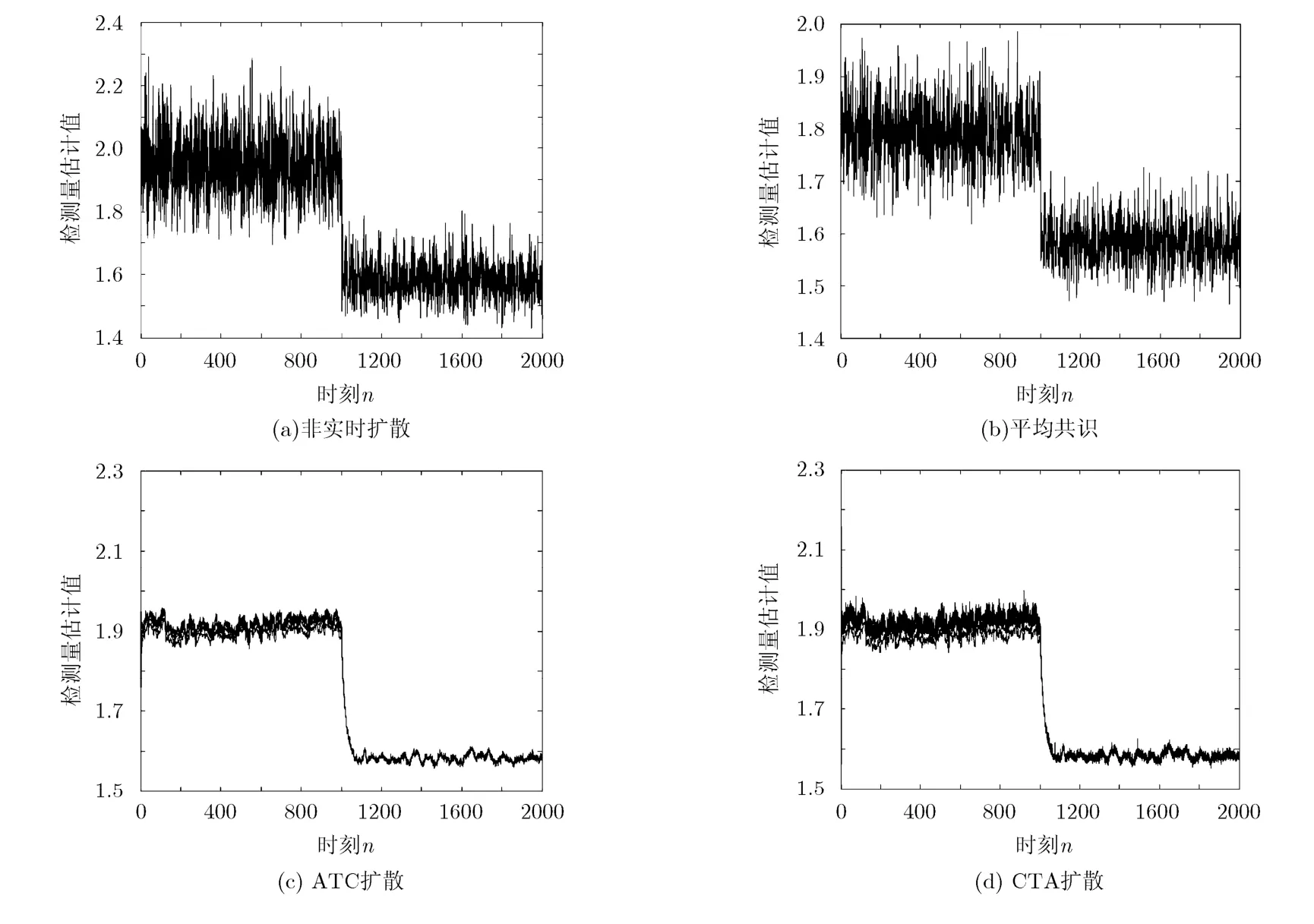
圖4 4種分布式算法的檢測量估計(jì)

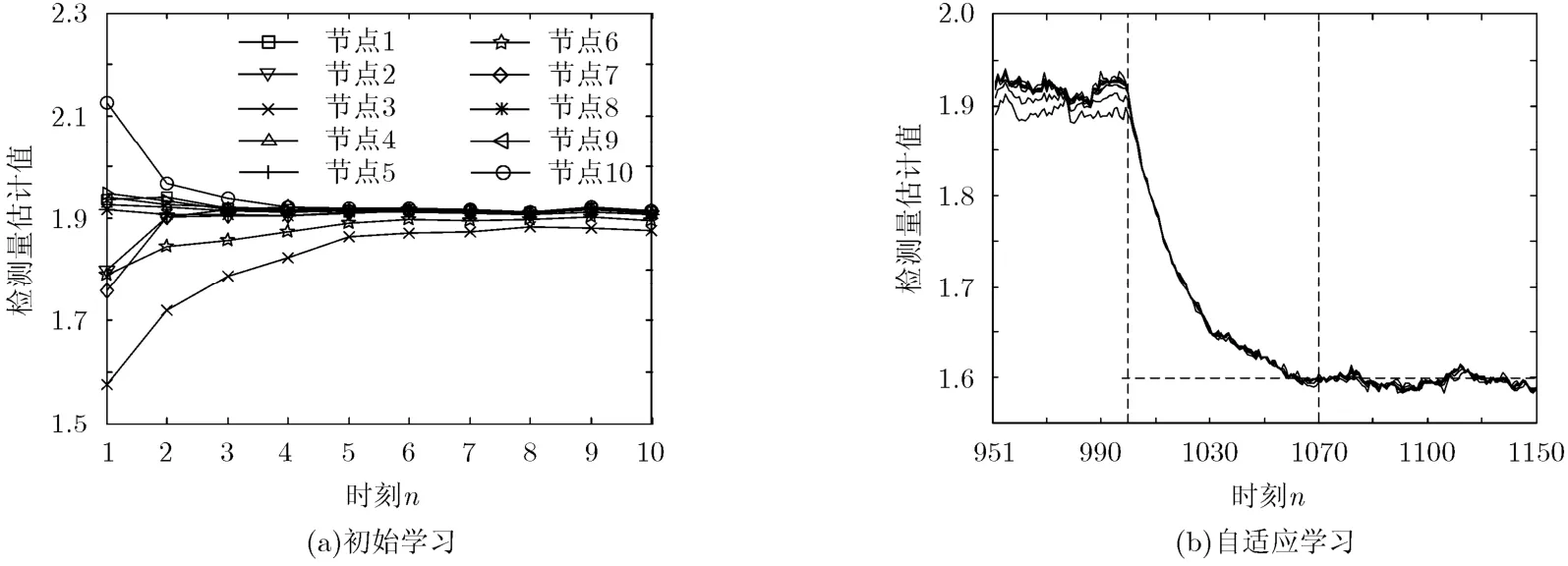
圖5 ATC算法的初始學(xué)習(xí)和自適應(yīng)學(xué)習(xí)曲線

圖6是兩種分布式擴(kuò)散算法的網(wǎng)絡(luò)瞬態(tài)方差性能和認(rèn)知節(jié)點(diǎn)的穩(wěn)態(tài)方差性能。圖6（a）是前300個(gè)檢測時(shí)刻網(wǎng)絡(luò)的瞬態(tài)方差性能，描述了每一個(gè)檢測時(shí)刻所有節(jié)點(diǎn)檢測量估計(jì)值的穩(wěn)定性，可以看出，ATC擴(kuò)散策略的方差曲線在CTA策略的下方，且趨于穩(wěn)定的速度更快，因此ATC擴(kuò)散策略所得的檢測量估計(jì)值的瞬態(tài)方差性能優(yōu)于CTA擴(kuò)散策略。圖6（b）是各個(gè)節(jié)點(diǎn)的穩(wěn)態(tài)方差性能。實(shí)驗(yàn)對網(wǎng)絡(luò)迭代穩(wěn)定之后10個(gè)節(jié)點(diǎn)最后的100次檢測量估計(jì)值做方差，可以看出，ATC擴(kuò)散策略下的所有節(jié)點(diǎn)的方差值均低于CTA擴(kuò)散策略。ATC擴(kuò)散算法的一次協(xié)作過程包括兩次信息交換，信息融合更加徹底，而CTA擴(kuò)散算法只有一次，提高了融合效率。兩種算法的本質(zhì)就是融合效率和融合精度的折中，因此采用ATC擴(kuò)散策略的網(wǎng)絡(luò)，瞬時(shí)性能和穩(wěn)態(tài)性能都優(yōu)于CTA擴(kuò)散策略。平均共識(shí)策略和非實(shí)時(shí)擴(kuò)散策略的估計(jì)值是認(rèn)知節(jié)點(diǎn)經(jīng)過數(shù)次迭代得到的一致收斂值，在同一時(shí)刻，因此考慮其瞬態(tài)方差沒有意義。

5.2 檢測性能分析

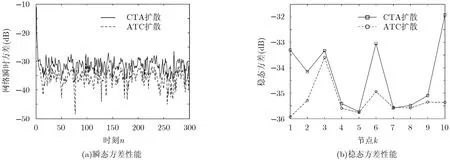
圖6 擴(kuò)散算法的性能曲線

圖7是4種分布式策略的檢測性能曲線。虛警概率取 0.01，橫坐標(biāo)是所有節(jié)點(diǎn)的平均信噪比，縱坐標(biāo)是檢測概率。從圖7中可以看出ATC擴(kuò)散策略和 CTA擴(kuò)散策略的檢測性能明顯優(yōu)于平均共識(shí)策略和非實(shí)時(shí)擴(kuò)散策略，ATC擴(kuò)散策略稍優(yōu)于 CTA擴(kuò)散策略。平均信噪比在-23 dB時(shí)，ATC擴(kuò)散策略就能達(dá)到 0.9的檢測概率，能夠滿足在極低信噪比條件下的PU信號檢測。在檢測概率為0.9時(shí)，實(shí)時(shí)擴(kuò)散策略檢測性能較非實(shí)時(shí)擴(kuò)散策略和平均共識(shí)策略，信噪比降低了大約6 dB。采用非實(shí)時(shí)擴(kuò)散策略和平均共識(shí)策略的認(rèn)知網(wǎng)絡(luò)，把整個(gè)感知過程分為了單節(jié)點(diǎn)檢測過程和協(xié)作過程，協(xié)作時(shí)所有節(jié)點(diǎn)多次信息交換使檢測量達(dá)到一致時(shí)，各個(gè)認(rèn)知節(jié)點(diǎn)獨(dú)自做出判決，而采用ATC擴(kuò)散策略和CTA擴(kuò)散策略的網(wǎng)絡(luò)，認(rèn)知節(jié)點(diǎn)的協(xié)作過程融合更多的檢測量信息，感知過程不需要所有節(jié)點(diǎn)檢測量完全一致，就能做出實(shí)時(shí)判決，從效果上看檢測性能發(fā)生了質(zhì)變。

6 結(jié)束語

本文研究了分布式認(rèn)知網(wǎng)絡(luò)的實(shí)時(shí)協(xié)作頻譜檢測問題，提出基于擴(kuò)散策略的分布式協(xié)作的實(shí)時(shí)檢測策略。實(shí)驗(yàn)仿真結(jié)果表明，基于擴(kuò)散策略的分布式協(xié)作的實(shí)時(shí)檢測算法能夠有效解決認(rèn)知節(jié)點(diǎn)的實(shí)時(shí)檢測問題，并能夠快速適應(yīng)PU信號有無的變化，提高認(rèn)知節(jié)點(diǎn)的檢測精度。采用ATC擴(kuò)散策略的認(rèn)知網(wǎng)絡(luò)在協(xié)作性能上稍優(yōu)于CTA擴(kuò)散策略，而采用CTA擴(kuò)散策略的網(wǎng)絡(luò)在協(xié)作效率上有一定優(yōu)勢。融合矩陣、自適應(yīng)矩陣的選取原則以及步長參數(shù)的選取對擴(kuò)散算法的性能影響較大，下一步將對此進(jìn)行研究。

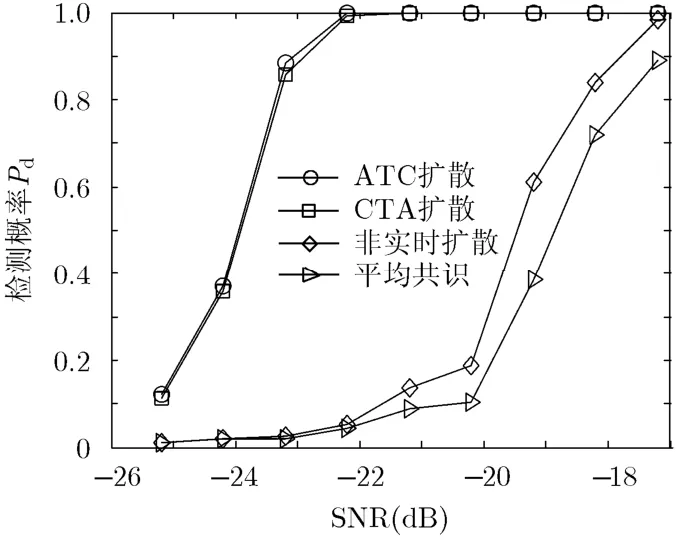
圖7 檢測性能曲線

［1］ Wu Q H， Ding G R， Wang J L， et al.. Consensus-based decentralized clustering for cooperative spectrum sensing in cognitive radio networks［J］. Chinese Science Bulletin， 2012，57（28/29）: 3677-3683.

［2］ Zeng Y， Liang Y C， Hoang A T， et al.. A review on spectrum sensing for cognitive radio: challenges and solutions［J］. EURASIP Journal on Advances in Signal Processing， 2010，DOI: 10.1155/2010/381465.

［3］ Bogdanovie N， Plata-Chaves J， and Berberidis K. Distributed diffusion-based LMS for node-specific parameter estimation over adaptive networks［C］. 2014 IEEE International Conference on Acoustics Speech and Signal Processing（ICASSP）， Florence， Italy， 2014: 7223-7227.

［4］ Raza A， Ejaz W， Ahmed S S， et al.. Consensus-based distributive cooperative spectrum sensing for mobile Ad hoc cognitive radio networks［OL］. http://dx.doi.org/ 10.1155/2013/450626. 2013.

［5］ Zhang W， Wang Z， Guo Y， et al.. Distributed cooperative spectrum sensing based on weighted average consensus［C］. IEEE Global Telecommunications Conference （GLOBECOM 2011）， Houston， TX， USA， 2011: 1-6.

［6］ Tu S Y and Sayed A H. Diffusion strategies outperform consensus strategies for distributed estimation over adaptive networks［J］， IEEE Transactions on Signal Processing， 2012，60（12）: 6217-6234.

［7］ Cattivelli F S and Sayed A H. Diffusion LMS strategies for distributed estimation［J］. IEEE Transactions on Signal Processing， 2010， 58（3）: 1035-1048.

［8］ Chen J and Sayed A H. Diffusion adaptation strategies for distributed optimization and learning over networks［J］. IEEE Transactions on Signal Processing， 2012， 60（8）: 4289-4305.

［9］ Ainomae A， Trump T， and Bengtsson M. Distributed diffusion LMS based energy detection［C］ 2014 6th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops （ICUMT）， St. Petersburg， 2014: 176-183.

［10］ Cattivelli F S and Sayed A H. Distributed detection over adaptive networks using diffusion adaptation［J］. IEEE Transactions on Signal Processing， 2011， 59（5）: 1917-1932.

［11］ Takahashi N， Yamada I， and Sayed A H. Diffusion least-mean squares with adaptive combiners: Formulation and performance analysis［J］. IEEE Transactions on Signal Processing， 2010， 58（9）: 4795-4810.

［12］ Al-Sayed S， Zoubir A M， and Sayed A H. Robust distributed detection over adaptive diffusion networks［C］ 2014 IEEE International Conference on Acoustics Speech and Signal Processing （ICASSP）， Florence， Italy， 2014: 7233-7237.

［13］ Braca P， Marano S， Matta V， et al.. Asymptotic performance of adaptive distributed detection over networks［OL］. http://arxiv.org/abs/1401. 5742. 2014.

［14］ Zeng Y and Liang Y C. Eigenvalue-based spectrum sensing algorithms for cognitive radio［J］. IEEE Transactions on Communications， 2009， 57（6）: 1784-1793.

［15］ 趙曉暉， 李曉燕. 認(rèn)知無線電中基于陣列天線和協(xié)方差矩陣的頻譜感知算法［J］. 電子與信息學(xué)報(bào)， 2014， 36（7）: 1693-1698. Zhao Xiao-hui and Li Xiao-yan. Spectrum sensing algorithm in cognitive radio based on array antenna and covariance matrix［J］. Journal of Electronics & Information Technology，2014， 36（7）: 1693-1698.

［16］ 袁龍， 邢祿， 彭濤， 等. 基于精確噪聲估計(jì)的迭代頻譜感知算法［J］. 電子與信息學(xué)報(bào)， 2014， 36（3）: 655-661. Yuan Long， Xing Lu， Peng Tao， et al.. An iterative spectrum sensing algorithm based on accurate noise estimation［J］. Journal of Electronics & Information Technology， 2014， 36（3）: 655-661.

張政保： 男，1965年生，教授，碩士生導(dǎo)師，研究方向?yàn)檎J(rèn)知無線電、信息安全技術(shù).

姚少林： 男，1992年生，碩士，研究方向?yàn)檎J(rèn)知無線電頻譜感知.

許 鑫： 男，1964年生，高級工程師，主要研究領(lǐng)域?yàn)橥ㄐ趴垢蓴_技術(shù).

劉廣凱： 男，1990年生，碩士，主要研究領(lǐng)域?yàn)橥ㄐ趴垢蓴_技術(shù).

Real-time Distributed Cooperative Spectrum Detection Algorithm Based on Diffusion Strategy

Zhang Zheng-bao Yao Shao-lin Xu Xin Liu Guang-kai
（Department of Information Engineering， Ordnance Engineering College， Shijiazhuang 050003， China）

Considering the problem of real-time distributed cooperative spectrum detection of cognitive users， a real-time distributed cooperative spectrum detection algorithm based on diffusion strategy is proposed. Global cost function can be approximated by an alternative localized cost that is amenable to distributed optimization. Each individual node optimizes this alternative cost via a steep-descent procedure that relies solely on interaction within the neighborhood of the node. The local estimate value can be calculated via the iteration procedure. A genera model for analyzing the mean and variance of the estimates of the diffusion strategy is derived. The formulas of ?probability of detection， probability of false alarm and detection threshold are derived. Theoretical analysis and lexperimental results show that the proposed algorithm can effectively solve the problem of real-time detection signal， can quickly learn and adapt to environmental changes. Compared with average consensus strategy and non-real-time diffusion strategy， the average SNR of the proposed algorithm reduces about 6 dB， while the Pfa ?below 0.01 and Pd reached to 0.9. The diffusion strategy can satisfy the signal detection in very low SNR.

Cognitive radio； Cooperative spectrum sensing； Distributed estimation； Diffusion strategy； Consensus strategy

TN92

A

1009-5896（2015）12-2858-08

10.11999/JEIT150460

2015-04-22；改回日期：2015-07-03；網(wǎng)絡(luò)出版：2015-08-28

*通信作者：姚少林 953285626@qq.com