基于高階內模的非線性離散系統迭代學習控制

周 偉，于 淼

（浙江大學 電氣工程學院，浙江 杭州310027）

自Arimoto等［1-2］針對工業機械手系統可重復的特點，提出一種迭代學習算法以來，這種智能控制技術［3-4］引起了人們極大的興趣.迭代學習控制將非線性系統作為研究對象，通過不斷迭代而達到期望行為.在迭代學習控制的發展過程中涌現了許多熱點問題，得到了諸多專家學者的關注，如經典迭代學習控制［5］、高階迭代學習控制［6］、魯棒迭代學習控制、最優迭代學習控制、自適應迭代學習控制［7］等.短短二十幾年，迭代學習控制獲得了極大的發展.

迭代學習控制本質上是通過對輸出誤差的不斷修正，而實現自我學習的［8-9］.利用前一次或前幾次操作時測得的誤差信息修正控制輸入，控制器的綜合結構簡單，在線計算負擔小［10］.針對非線性系統，使用時變的學習控制技術可以改善控制性能［11］.尤其當模型未完全已知，或不能充分展現被控對象的全部客觀規律時，迭代學習控制可以充分利用被控對象可以重復運行的特點，不斷更新控制輸入，通過多次迭代后，實現對系統參考輸出軌跡的零誤差追蹤［12］.

傳統的迭代學習控制在追蹤參考軌跡的過程中，要求參考軌跡必須是迭代不變的.然而，實際上很難滿足如此嚴格的重復性［13］.比如，機械手在上一次工作過程中，在［0 ，T ］期間追蹤某一參考軌跡，在下一次工作時，可能追蹤另一相關的參考軌跡.根據內模原理可知，當受控對象追蹤某一目標軌跡時，控制回路必須包含產生目標軌跡的動力系統模型的全部信息［14］.Moore［15］首先引入ω 算子用來描述迭代域的變化情況.Liu等［16］針對連續系統參考軌跡的迭代域非嚴格重復性問題，通過將高階內模和迭代學習控制方法相結合，利用λ范數，證明了基于高階內模的迭代學習方法的有效性.Yin等［17］針對帶不確定參數的非線性系統的迭代學習問題，使用高階內模描述時變且沿迭代域變化的參數，設計基于高階內模的參數學習律，并用Lyaponov方法證明了迭代域的漸近收斂.隨著計算機控制技術的廣泛應用，離散系統的控制問題受到越來越多的重視.尤其當系統中存在非線性因素時，無法將連續系統中已經得到的結論直接應用于離散系統.另外，迭代學習過程的實現總是離散的.針對離散系統，研究參考軌跡的迭代域非嚴格重復問題具有現實意義.

本文針對一類一階非正則離散時間非線性系統參考軌跡的非嚴格重復性問題，提出基于內模原理的控制方法.針對由高階內模產生的參考軌跡，使用一種D 型迭代學習控制律，從理論上證明了系統跟蹤誤差的收斂性.對于機械手模型的仿真結果證明了所提出方法的有效性.

1 問題描述

系統方程如下式所示：

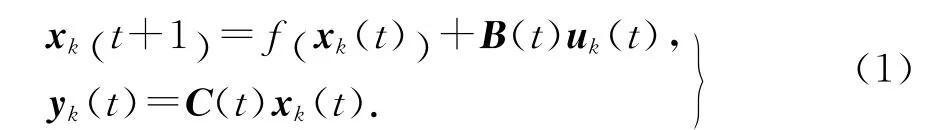
式中：下標k表示迭代次數；t∈［0 ，T ］，［0 ，T ］表示離散時間｛0，1，…，T ｝；xk（t）∈Rn；uk（t）和yk（t）分別為第k 次迭代時的輸入和輸出向量，uk（t）∈Rm，yk（t）∈Rm；f （xk（t））∈Rn；B（t）∈Rn×m、C（t）∈Rm×n均為關于t的有界函數.系統（1）為離散一階非正則系統，在有限時間區間［0 ，T ］上重復運行.

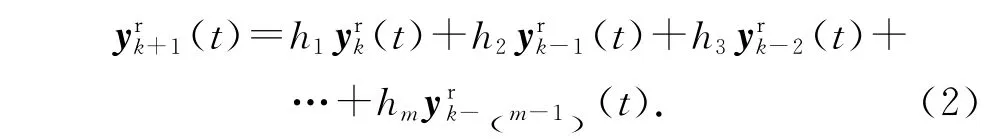
式中：hi（i＝1，2，…，m）為穩定的多項式 H （z） ＝zm-h1zm-1-h2zm-2-…-hm的系數.式（2）描述了參考軌跡迭代域變化的規律性.由式（2）可以看出，參考軌跡迭代相關，且變化規律是已知的.另外，根據m 階內模求得參考軌跡（t），需要m 個初始軌跡（t），（t），…，（t）.記 多 項 式 算 子H （ω-1）為

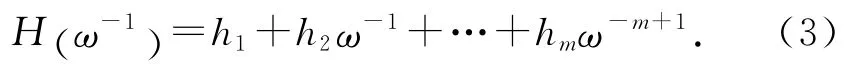
將式（2）改寫為

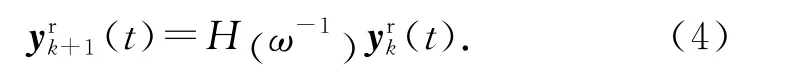
系統（1）滿足如下假設.

假設1 非線性函數f （xk（t））在有限時間區間［0 ，T ］上關 于xk滿 足 一 致 全局Lipschitz條 件，即滿足：‖f （x1）-f （x2）‖≤lf‖x1-x2‖，其中lf為Lipschitz系數.

假設2 系統初值條件滿足：ek（0） ＝0，k＝1，2，….

假設3 m 階內模生成的參考軌跡滿足：多項式 H （z） ＝zm-h1zm-1-h2zm-2-…-hm是 穩 定的，即多項式的特征方程的所有根位于單位圓內部，或在單位圓上僅有單根或共軛復根.

系統輸出追蹤由m 階內模生成的參考軌跡，首先，隨著迭代次數的增加，參考軌跡不能趨于發散.因此，上述多項式構成的特征方程的根必須位于單位圓內部，或僅有單根或共軛復根落在單位圓上.其次，若上述多項式構成的特征方程的根全部位于單位圓的內部，上述多項式是穩定的，并且當迭代次數趨向無窮時，由m 階內模生成的參考軌跡最終會收斂到零.因為這種情況下，由m 階內模產生的參考軌跡的變化趨勢是漸近穩定的.最后，若特征方程至少在單位圓上有單根或共軛復根，則由m 階內模生成的參考軌跡在迭代域上會不斷變化，且不會收斂到零.

例如，當H1（ω-1）＝1 時，有（t）＝（t），追蹤的參考軌跡迭代域不變，屬于高階內模生成的參考軌跡的特殊情況.當H2（ω-1）＝ω-1時，高階內模生成的參考軌跡滿足的多項式為H2（z） ＝z2-1，特征根為z1，2＝±1，都位于單位圓上.此時，（t）＝（t）.基于迭代域的算子ω 的定義來源于z 變換的概念，因此仿照z 變換的方法求解（t）可得，y（t）＝D1（t）·1k＋D2（t）·（- 1 ）k.其中，D1（t）及D2（t）為與迭代無關的待定時變系數，由初始條件決定.這意味著在奇數次迭代時，追蹤的參考軌跡都相同，即（t）＝D1（t）-D2（t）＝…＝（t）；在偶數次迭代時，追蹤的參考軌跡相同，即（t）＝D1（t）＋D2（t）＝…＝（t），k＝1，2，…，N.由此可見，由高階內模H2（ω-1）生成的參考軌跡在迭代域上，以2次迭代為周期，參考軌跡會發生重復性變化，但是不會收斂到零.

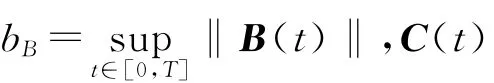
定義1 函數f（t）的λ范數［21］為

定義2 表征m 階內模的多項式算子H （ω-1）和輸出追蹤誤差乘積的λ范數為

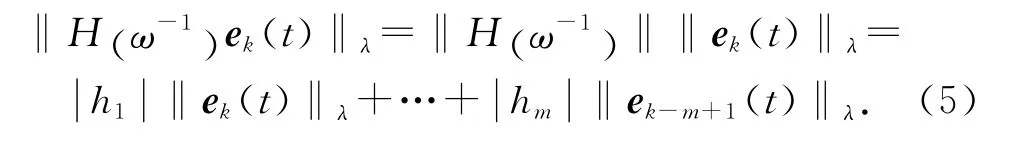
2 迭代學習控制律的設計

控制目標是設計迭代學習控制律uk＋1（t），使得當k→∞時，

針對基于高階內模的參考軌跡，采用含有m 階內模的D 型迭代學習控制律：

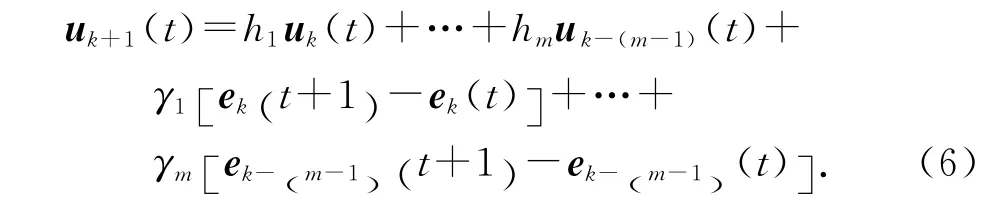
即

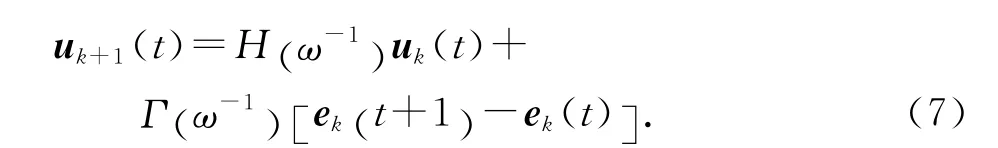
其中H （ω-1）的定義如式（3）所示，學習增益γk的定義為

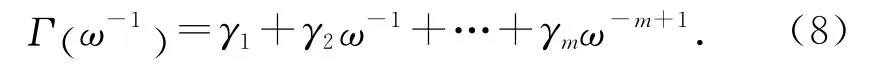
定理：對于滿足假設1、2、3和4的一階非正則離散時間非線性系統（1），針對參考軌跡（2），采用含有m 階內模的D 型迭代學習控制律（6），選擇學習增益γk，使得下列特征多項式漸近穩定：

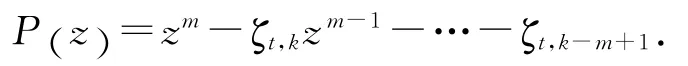
式中：ζt，j＝‖hk＋1-jIm-C（t）B （t- 1）γk＋1-j‖，Im∈Rm×m為單位矩陣，t∈［1 ，T＋1］ ，j∈［k，k-1，…，km＋1］，系統跟蹤誤差沿迭代方向收斂到0，即

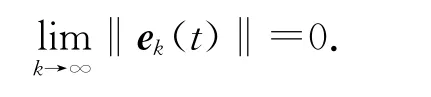
3 收斂性證明

定義第k＋1次迭代時的輸出追蹤誤差為

將滿足m 階內模的輸出跟蹤軌跡（4）代入可得

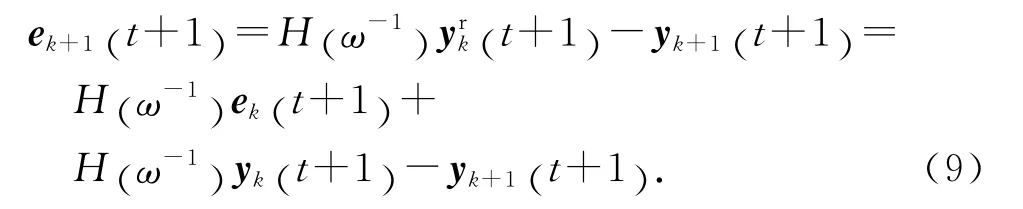
將式（1）代入式（9），可得

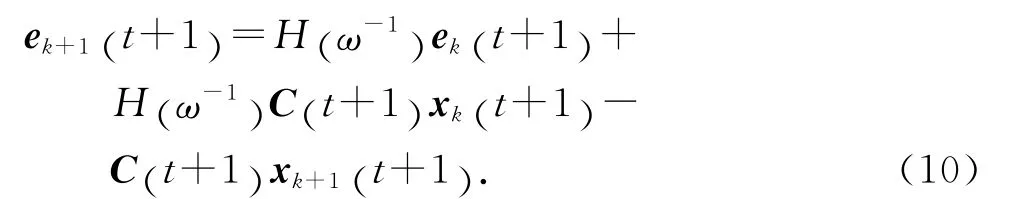
整理可得

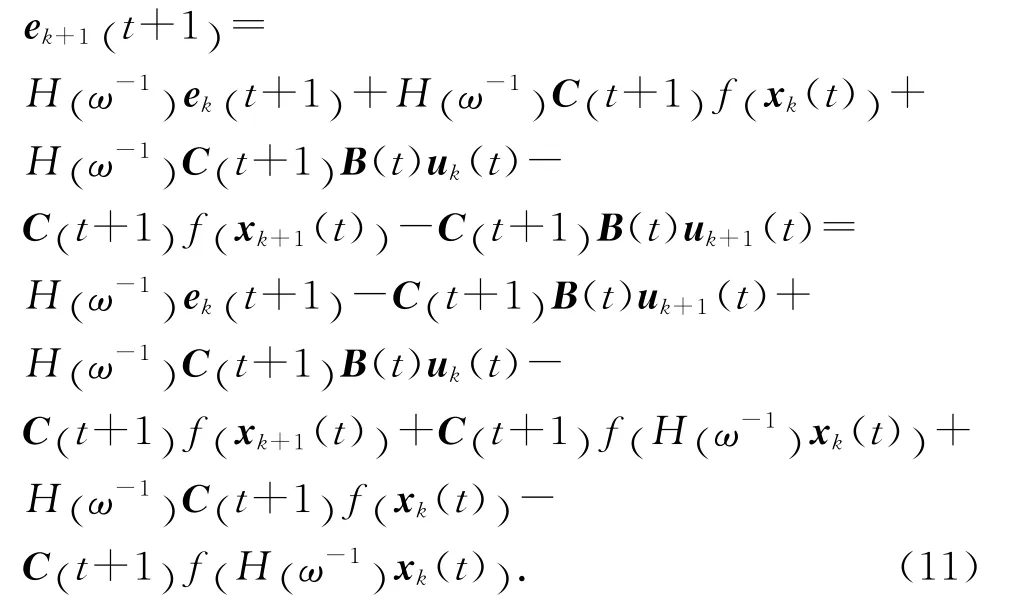
由式（3）、（4）可知，

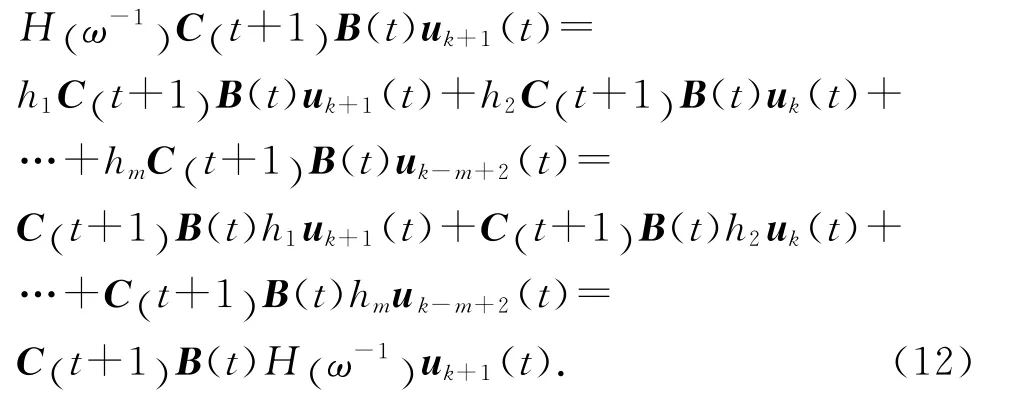
對式（11）兩端取范數，并將式（7）代入可得

在式（13）中，令

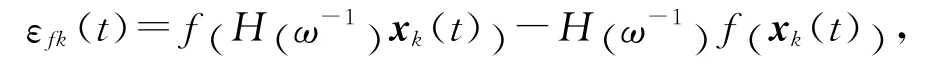
并整理可得

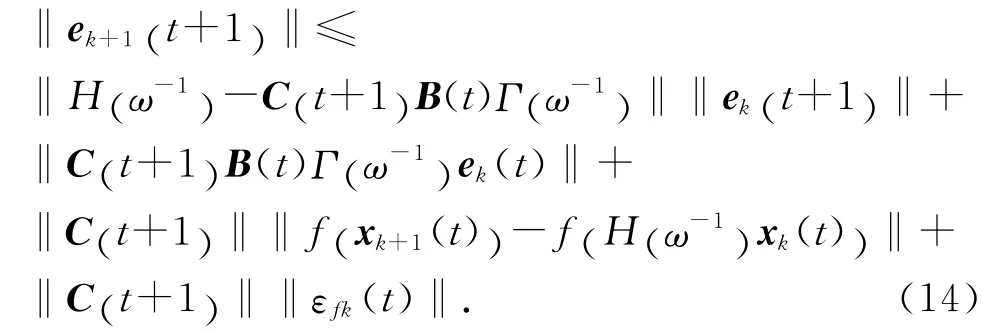
考慮到函數f（t）滿足假設1，式（14）可變為

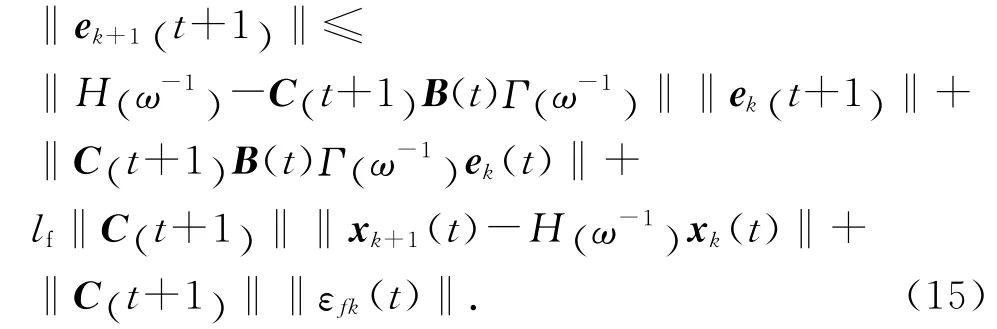
由式（1）可得

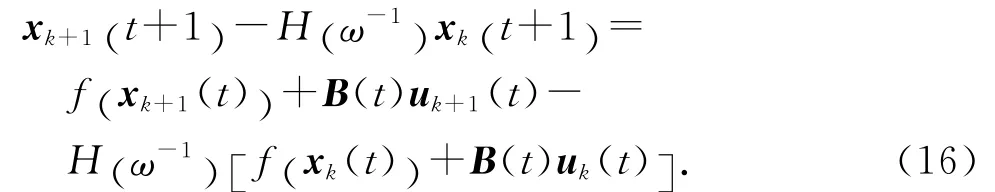
根據式（13），對式（16）兩端取范數可得

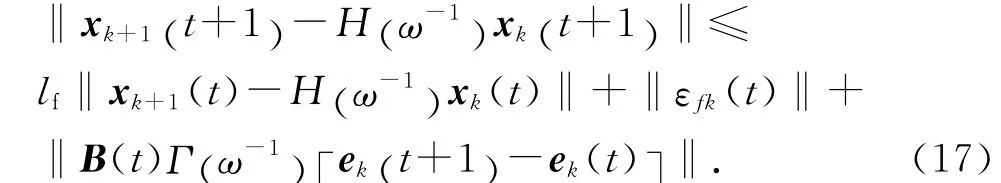
然后將式（17）在t∈［0 ，T ］展開.當t＝0時，有

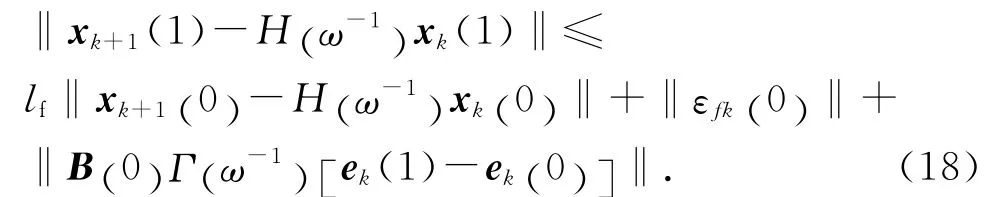
根據假設2可知，

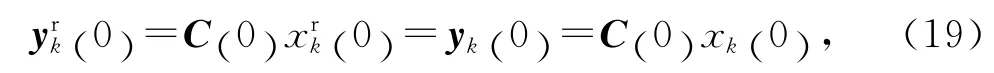
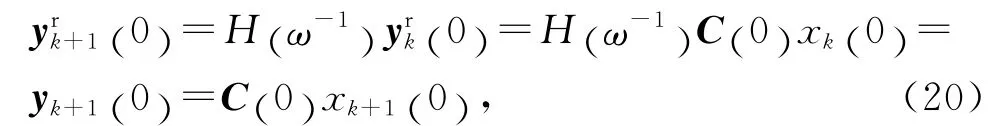
可得：xk＋1（0） ＝H （ω-1）xk（0） .將其代入式（18），有

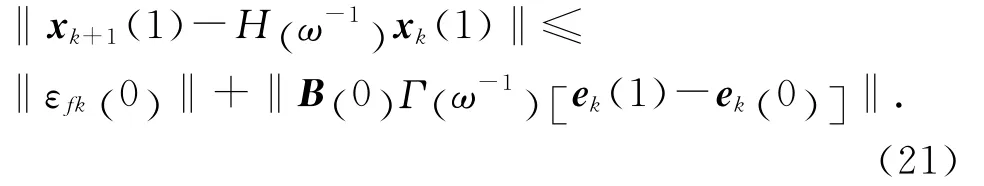
同理有

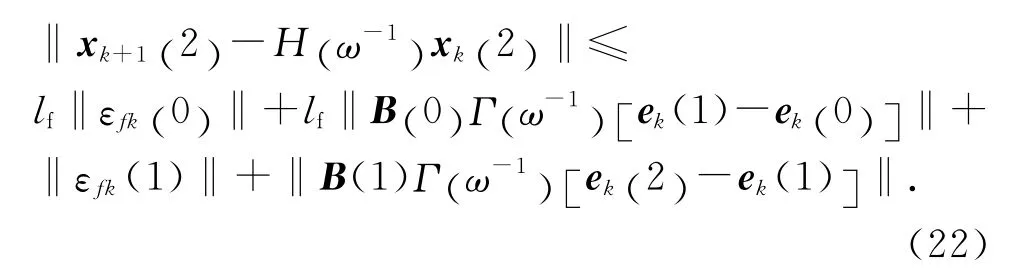
依此類推，可得

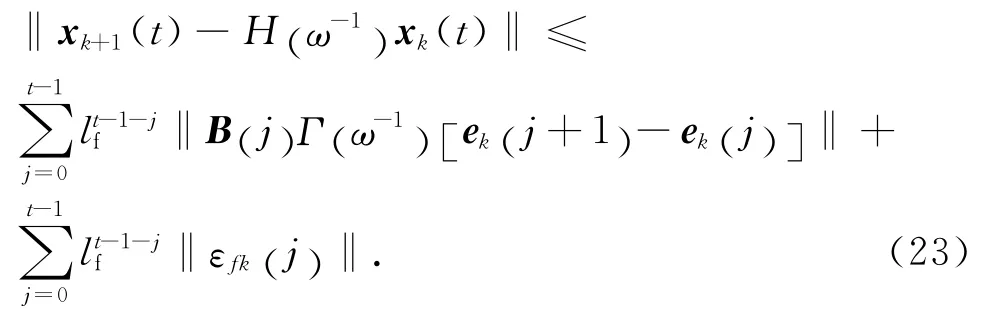
將式（23）代入式（15），有

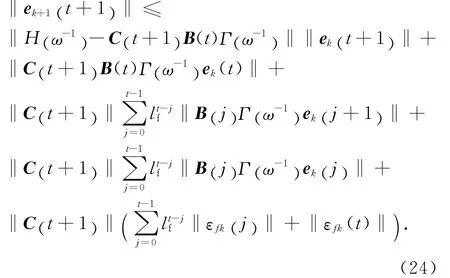
將式（24）兩端同時乘以exp（-λ（t ＋1） ），然后在區間［0 ，T ］上取上界；根據假設4，可得

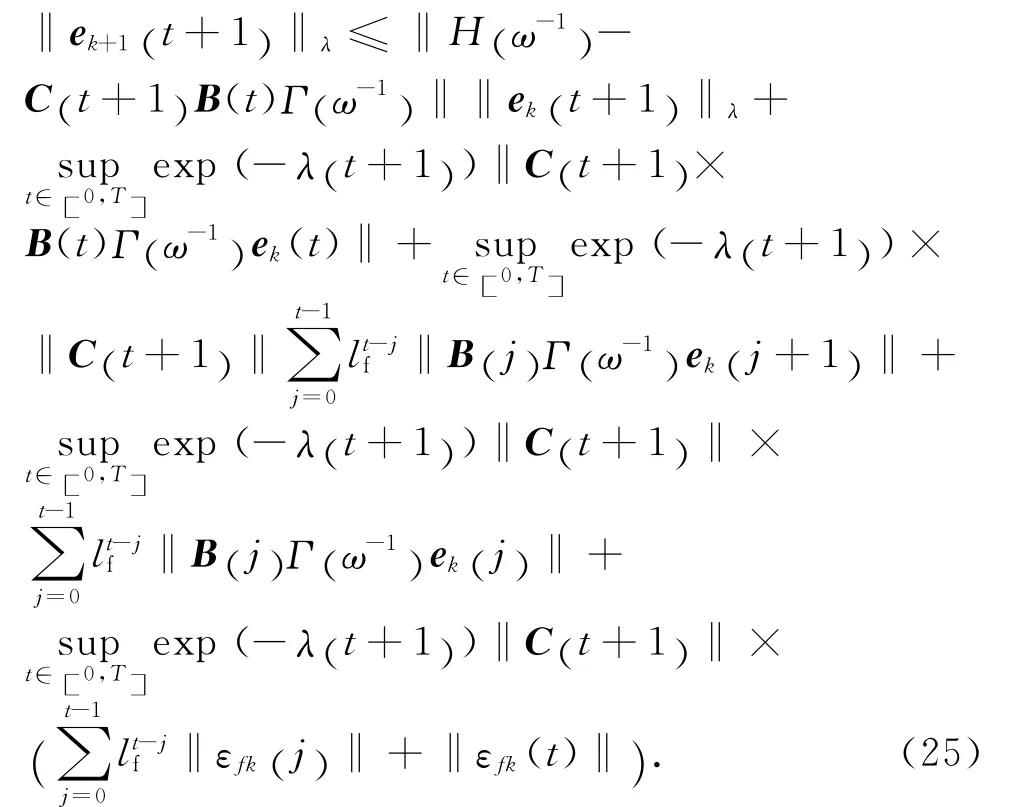
在式（25）中，可得

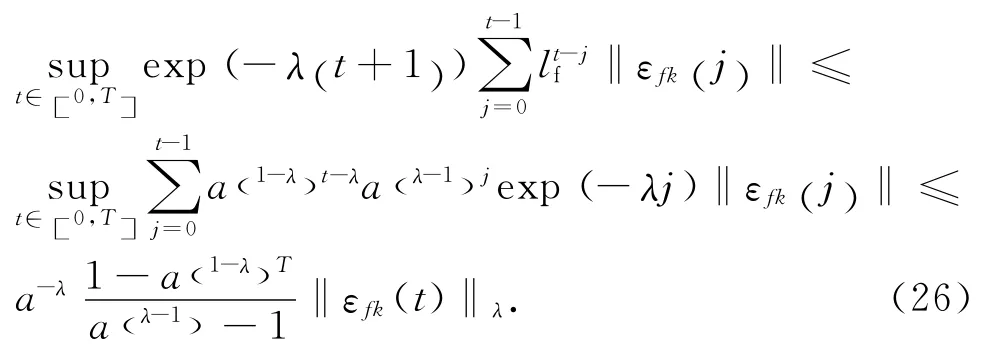
式中：

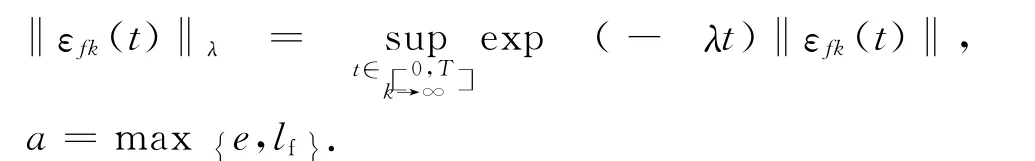
同理可得

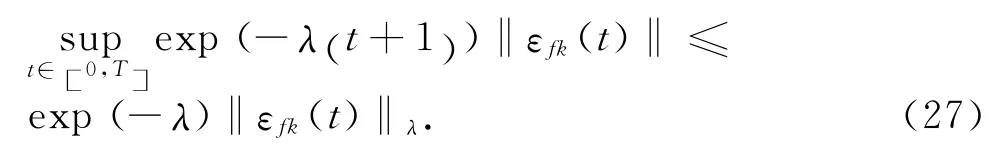
另外，可得

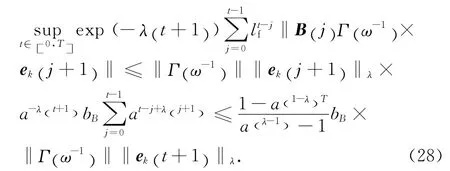
同理有，

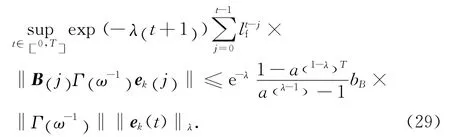
將式（26）～（29）代入式（25）可知，

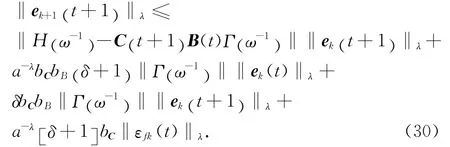
式中：

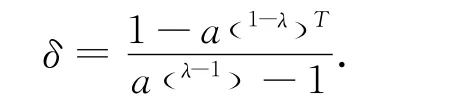
將式（30）各項中的高階內模完整表示出來，則有

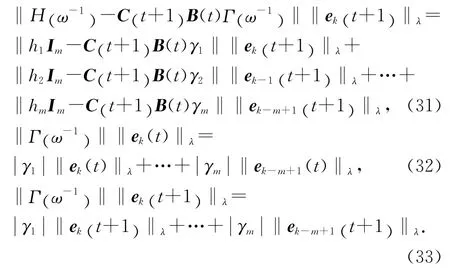
將式（31）～（33）代入式（30），再將式（30）由t＝0到t＝T逐項寫出，并記αt＋1＝a-λbC［δ＋ 1］ ‖εfk（t）‖λ，t∈［0 ，T］ ，可知，當t＝0時，有

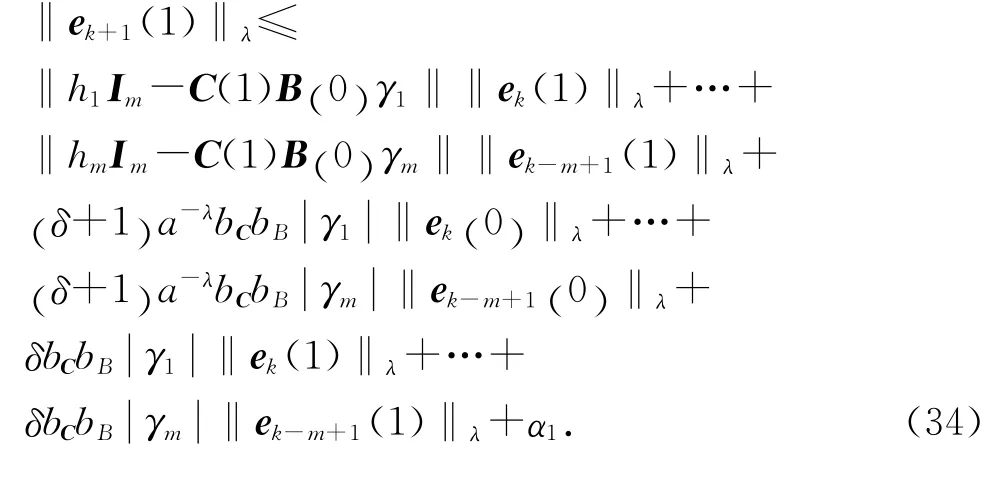
同理，逐步推知，當t＝T 時，有

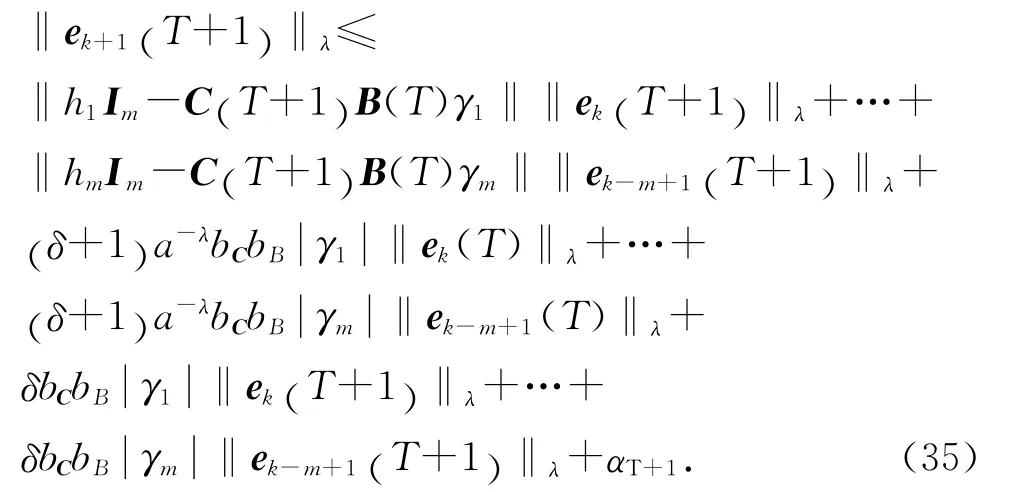
注意到假設2，對不等式（35）進行整理，并令

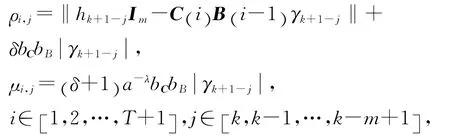
可知，當t∈［0 ，T］ 時，有

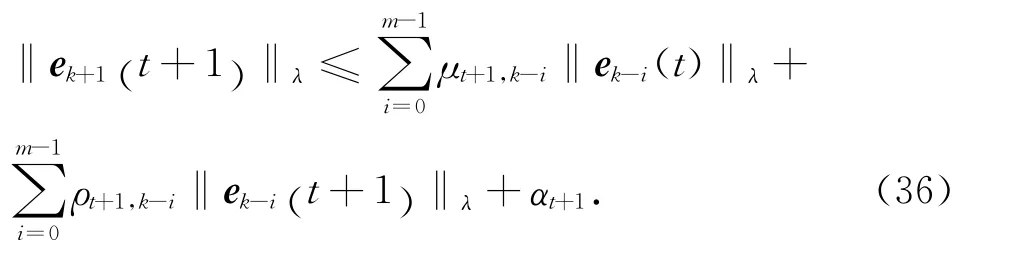
當t＝0時，滿足

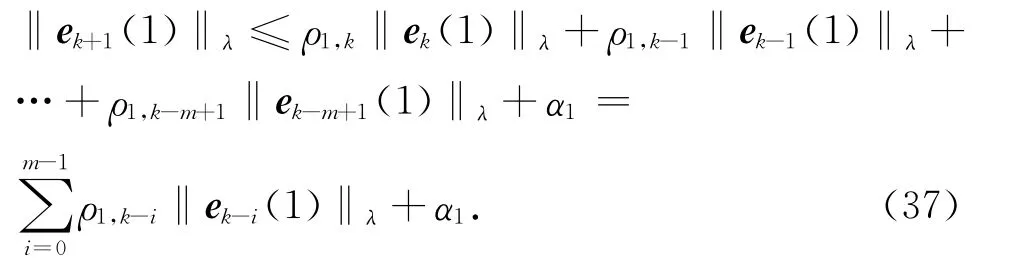
將t＝0到t＝T 的每一項展開并寫成矩陣形式如下：

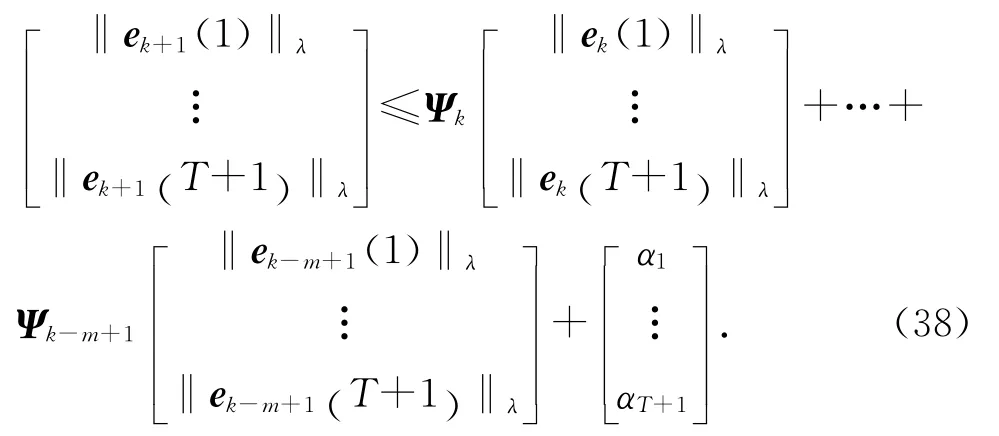
式中：

當k＝0時，有

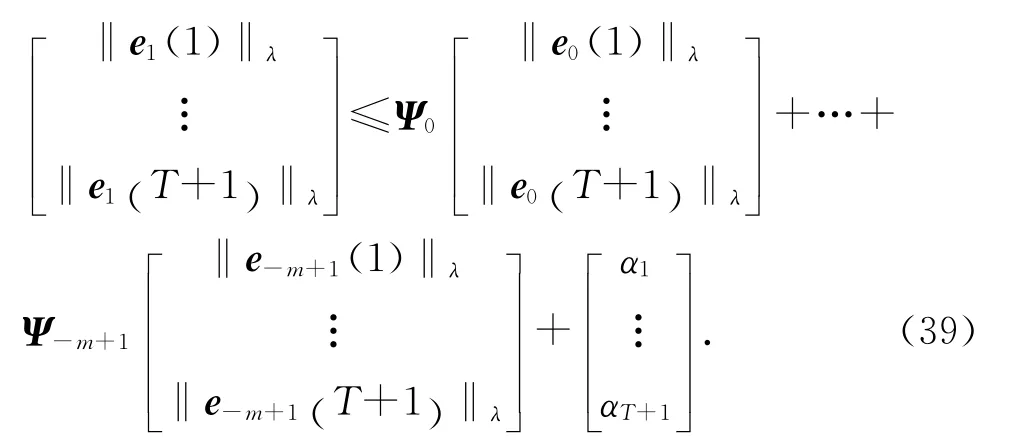
式中：Ψs（s∈［1-m，2-m，…，0］ ），滿足

首先分析不等式（36）中的μt＋1，j和ρt＋1，j.可以看出，當λ取足夠大時，μt＋1，j以及ρt＋1，j中的δ可以達到任意小.其次，分析αt＋1，t∈［0 ，T ］.可以看出，αt＋1中的‖εfk（t）‖λ是關于λ的函數.由于

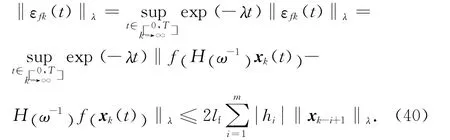
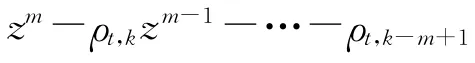
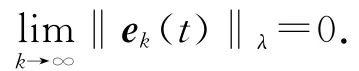
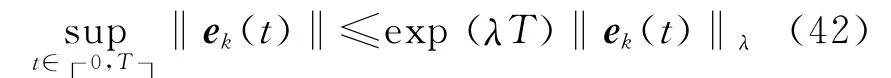
4 仿真結果

考慮單連桿機械手的軌跡跟蹤問題.單連桿機械手模型的系統方程［22-24］為

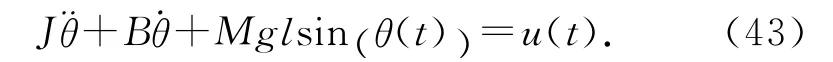
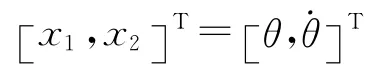
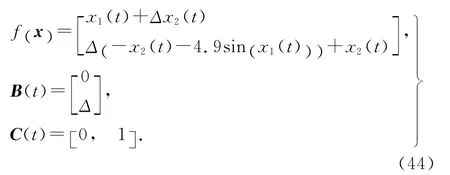
由于C（ t＋ 1 ）B（t）＝［0 ，1］ ［0，Δ］T≠0，可知系統為一階非正則.

追蹤的參考軌跡為

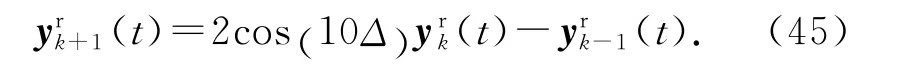
其中第一次及第二次迭代的追蹤軌跡如下：

輸出追蹤參考軌跡中內含的二階內模系數為：h1＝2cos （10 Δ） ，h2＝-1，因此，控制取為

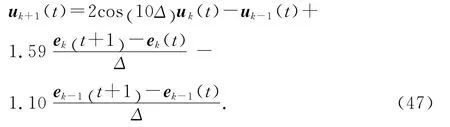
選 擇 學 習 增 益γ1＝1.59／Δ，γ2＝-1.10／Δ.（ek（t＋ 1） -ek（t））／Δ 是機械手系統（43）在 第k 次迭代時的輸出追蹤誤差的一階導數［25］，即控制輸入（47）可以看成是連續系統（43）的下述學習控制律的離散化：

收斂條件為：‖h1I-γ1CB‖＝0.4＜1，‖h2Iγ2CB‖＝0.1＜1.對應的特征多項式為：z2-0.4z-0.1.它的2個特征根分別為z1＝0.57，z2＝-0.17，都位于單位圓內.

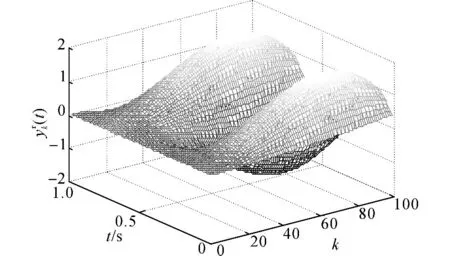
圖1 迭代變化的追蹤參考軌跡Fig.1 Iteration-varying reference trajectory

圖1給出參考軌跡在時域和迭代域下的變化情況.由式（45）可知，迭代變化的參考軌跡滿足，多項式 H （z） ＝z2-2cos （10 Δ） z＋1的特征根是一對位于單位圓上的共軛復根.仿照z 變換的方式求解式（45）可得，（t）＝Da（t）·cos （10 Δk） ＋Db（t）×sin （10 Δk） ，其中Da（t）及Db（t）為與迭代無關的待定時變系數，由初始條件決定.由此可知，參考軌跡（45）在迭代域上會不斷變化，不會重復，且不會收斂到零.從圖1可以看出，滿足m 階內模的參考軌跡（45）在迭代域內不斷振蕩，完全不重復.定義第k次迭代的輸出均方根誤差為

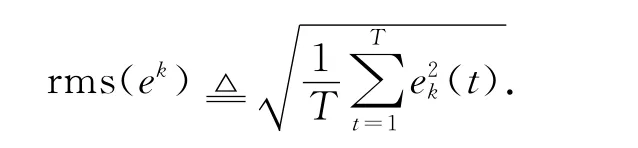
表1給出不同的迭代次數時，系統的輸出均方根誤差.圖2給出系統沿迭代方向的輸出均方根誤差.圖3展示了第3次、第7次及第10次迭代時系統的輸出追蹤情況.從圖2、3可以看出，隨著迭代次數的增加，系統輸出逐漸收斂到參考軌跡.第10次迭代時，系統輸出已經能夠很好地追蹤參考軌跡.另外，第3次迭代時追蹤的參考軌跡和第10次迭代時追蹤的參考軌跡完全不同，采用基于高階內模的D型迭代算法能夠很好地實現追蹤.當選擇輸出均方根誤差的許可范圍為小于0.01 時，從表1 可以看出，第8次迭代之后，系統的輸出均方根誤差都在許可范圍之內.

為了與本文含有m 階內模的D 型迭代學習控制律（47）相比較，給出含有m 階內模的P 型［26］迭代學習控制律的仿真結果.控制輸入如下式所示：

表1 基于高階內模的D型迭代學習律的輸出均方根誤差Tab.1 Output tracking root-mean-square error of HOIMbased D-type ILC

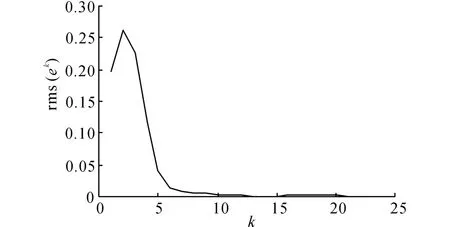
圖2 采用基于高階內模的D型迭代學習律的系統沿迭代方向的輸出均方根誤差Fig.2 Output tracking root-mean-square error of HOIM-based D-type ILC along iteration axis

圖3 第3、7及10次迭代時的追蹤Fig.3 Tracking profiles of HOIM-based ILC for 3rd，7th and 10th iterations

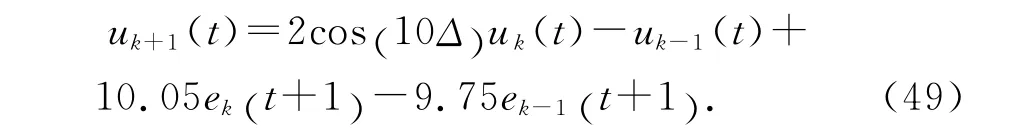
表2給出不同迭代次數時系統的輸出均方根誤差.系統沿迭代方向的輸出均方根誤差曲線如圖4所示.

考慮到含有高階內模的迭代學習控制律形式與傳統的高階迭代學習控制律形式相似，為了與采用高階內模的迭代學習控制對比，給出采用高階迭代學習律時的系統追蹤情況.選取控制輸入如下式所示：

表2 基于高階內模的P型迭代學習律的輸出均方根誤差Tab.2 Output tracking root-mean-square error of HOIMbased P-type ILC

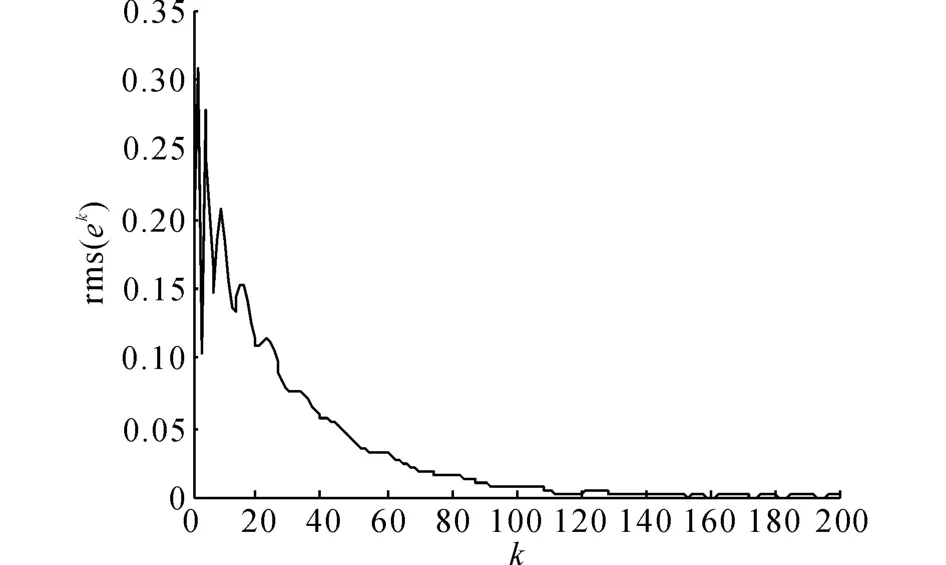
圖4 采用基于高階內模的P型迭代學習律的系統沿迭代方向的輸出均方根誤差Fig.4 Output tracking root-mean-square error of HOIM-based P-type ILC along iteration axis

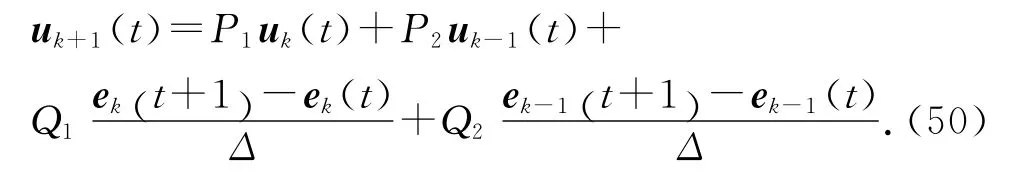
選擇P1＝1.91，P2＝-0.91，Q1＝2.65，Q2＝-1.圖5給出采用高階迭代學習算法，迭代100次時，系統的輸出均方根誤差曲線.表3給出不同的迭代次數時，系統的輸出均方根誤差.將圖4、5與圖2對比可見，采用基于高階內模的D 型迭代學習方法，與采用另外2種迭代學習控制方法相比，在收斂過程中的振蕩較少，收斂過程更加平穩，收斂速度顯著加快.

圖5 采用高階迭代學習算法時沿迭代方向的輸出均方根誤差Fig.5 Output tracking root-mean-square error with high order ILC algorithm along iteration axis

表3 基于高階迭代學習算法的輸出均方根誤差Tab.3 Output tracking root-mean-square error of high order ILC

5 結 論

（1）本文針對由高階內模產生的參考軌跡，設計基于高階內模的迭代學習控制，系統跟蹤誤差可以在有限時間內收斂到零.

（2）通過對機械手模型的離散化，然后設計學習增益，并進行仿真分析.可以發現，采用基于高階內模的D 型迭代學習控制方法能夠很好地追蹤迭代域變化的參考軌跡，經過較少的迭代次數能夠達到系統追蹤的要求.

（3）針對追蹤軌跡迭代域的非嚴格重復問題，高階迭代學習具有一定的魯棒性，但不能達到漸近收斂.

（

）：

［1］ARIMOTO S，KAWAMURA S，MIYAZAKI F.Bettering operation of robots by learning［J］.Journal of Robotic Systems，1984，1（2）：123-140.

［2］ARIMOTO S，KAWAMURA S，MIYAZAKI F.Bettering operation of dynamic systems by learning：a new control theory for servomechanism or mechatronics systems［C］∥Proceedings of 23rd Conference on Decision and Control.Las Vegas：IEEE，1984：1064-1069.

［3］張興國，林輝.迭代學習控制理論進展與展望［J］.測控技術，2006，25（11）：1-5.ZHANG Xing-guo，LIN Hui.Recent developments and prospects of iterative learning control theory［J］.Measurement and Control Technology，2006，25（11）：1-5.

［4］許建新，侯忠生.學習控制的現狀與展望［J］.自動化學報，2005，31（6）：943-955.XU Jian-xin，HOU Zhong-sheng.On learning control：the state of the art and perspective［J］.ACTA Automatica Sinica，2005，31（6）：943-955.

［5］ARIMOTO S.Learning control theory for robotic motion［J］.International Journal of Adaptive Control and Signal Processing，1990，4（6）：543-564.

［6］CHEN Yang-quan，WEN Chang-yun，SUN Ming-xuan.A robust high-order P-type iterative controller using current iteration tracking error［J］.International Journal of Control，1997，68（2）：331-342.

［7］FRENCH M，ROGERS E.Non-linear iterative learning by an adaptive Lyapunov technique［J］.International Journal of Control，2000，73（10）：840-850.

［8］王曄，劉山.期望軌跡可變的非線性時變系統迭代學習控制 ［J］.浙 江 大 學 學 報：工 學 版，2009，43（5）：839-843.WANG Ye，LIU Shan.Iterative learning control of nonidentical desired trajectories for a class of nonlinear timevarying systems［J］.Journal of Zhejiang University：Engineering Science，2009，43（5）：839-843.

［9］于淼，王佳森，齊冬蓮.具有未知控制方向的輸出反饋自適應學習控制［J］.浙江大學學報：工學版，2013，47（8）：1424-1430.YU Miao，WANG Jia-sen，QI Dong-lian.Output-feedback adaptive learning control with unknown control direction［J］.Journal of Zhejiang University：Engineering Science，2013，47（8）：1424-1430.

［10］孫明軒，黃寶健.迭代學習控制［M］.北京：國防工業出版社，2000：2-3.

［11］BONDI P，CASALINO G，GAMBARDELLA L.On the iterative learning control theory for robotic manipulators［J］.IEEE Journal of Robotics and Automation，1988，4（1）：14-22.

［12］馬航，楊俊友，袁琳.迭代學習控制研究現狀與趨勢［J］.控制工程，2009，16（3）：286-290.MA Hang，YANG Jun-you，YUAN Lin.Current state and trend of iterative learning control［J］.Control Engineering of China，2009，16（3）：286-290.

［13］XU Jian-xin.Direct learning of control efforts for trajectories with different magnitude scales［J］.Automatica，1997，33（12）：2191-2195.

［14］TAYEBI A，ZAREMBA M B.Internal model-based robust iterative learning control for uncertain LTI systems［C］∥Proceedings of the 39th IEEE Conference on Decision and Control.Sydney：IEEE，2000：3439-3444.

［15］MOORE K L.A matrix fraction approach to higher-order iterative learning control：2-D dynamics through repetition-domain filtering ［C］∥Proceedings of the Second International Workshop on Multidimensional（ND）Systems.Czocha Castle：［s.n.］，2000：99-104.

［16］LIU Chun-ping，XU Jian-xin，WU Jun.On iterative learning control with high-order internal models［J］.International Journal of Adaptive Control and Signal Processing，2010，24（9）：731-742.

［17］YIN Chen-kun，XU Jian-xin，HOU Zhong-sheng.A high-order internal model based iterative learning control scheme for nonlinear systems with time-iterationvarying parameters［J］.IEEE Transactions on Automatic Control，2010，55（11）：2665-2670.

［18］CHI Rong-hu，HOU Zhong-sheng，XU Jian-xin.Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition［J］.Automatica，2008，44（8）：2207-2213.

［19］LIU Chun-ping，XU Jian-xin，WU Jun.Iterative learning control with high-order internal model for linear time-varying systems［C］∥Proceedings of 2009 American Control Conference.St.Louis：IEEE，2009：1634-1639.

［20］CHEN Yang-quan，MOORE K L.Harnessing the nonrepetitiveness in iterative learning control［C］∥Proceedings of the 41st IEEE Conference on Decision and Control.Las Vegas：IEEE，2002：3350-3355.

［21］CHIEN C J.A discrete iterative learning control for a class of nonlinear time-varying systems ［J］.IEEE Transactions on Automatic Control，1998，43（5）：748-752.

［22］SUN Ming-xuan，WANG Dan-wei.Initial shift issues on discrete-time iterative learning control with system relative degree［J］.IEEE Transactions on Automatic Control，2003，48（1）：144-148.

［23］WANG Dan-wei.Convergence and robustness of discrete time nonlinear systems with iterative learning control［J］.Automatica，1998，34（11）：1445-1448.

［24］HWANG D H，BIEN Z，OH S R.Iterative learning control method for discrete-time dynamic systems［J］.IEE Proceedings-D：Control Theory and Applications，1991，138（2）：139-144.

［25］JANG T J，AHN H S，CHOI C H.Iterative learning control for discrete-time nonlinear systems［J］.International Journal of Systems Science，1994，25（7）：1179-1189.

［26］MOORE K L.An observation about monotonic convergence in discrete-time，P-type iterative learning control［C］∥Proceedings of the 2001IEEE International Symposium on Intelligent Control.Mexico：IEEE，2001：45-49.