基于信號(hào)體制的熱噪聲模型及對(duì)RAIM 的影響

賀 劉，姚 錚，崔曉偉，陸明泉，郭 婧

（1.清華大學(xué) 電子工程系，北京100084；2.中國(guó)民航科學(xué)技術(shù)研究院，北京100084）

隨著GPS與GLONASS的現(xiàn)代化，Galileo與我國(guó)北斗系統(tǒng)的建設(shè)，全球GNSS系統(tǒng)進(jìn)入了蓬勃發(fā)展時(shí)期，多模、多頻聯(lián)合導(dǎo)航已成為導(dǎo)航系統(tǒng)發(fā)展的主要趨勢(shì)［1］.由于測(cè)距源數(shù)量的倍增，客觀上增大了測(cè)距出現(xiàn)故障偏差的概率，熱噪聲、多徑、干擾等復(fù)雜環(huán)境將削弱測(cè)距的可靠性，觀測(cè)測(cè)距的完好性日趨重要.接收機(jī)完好性監(jiān)測(cè)（receiver autonomous integrity monitoring，RAIM）技術(shù)作為用戶端唯一的完好性監(jiān)測(cè)手段，通過(guò)故障檢測(cè)與排除（fault detect execution，F(xiàn)DE）算法，利用冗余觀測(cè)信息進(jìn)行一致性統(tǒng)計(jì)校驗(yàn)，剔除含粗差的故障測(cè)距，以提升測(cè)距置信度水平，進(jìn)而保證定位估計(jì)的準(zhǔn)確性.

由于受測(cè)距噪聲與接收設(shè)備熱噪聲的影響，測(cè)距觀測(cè)精度不完全相同，方差隨著俯仰角度及C／N0等多種因素相應(yīng)變化.在傳統(tǒng)加權(quán)RAIM 算法與模型 中， NIO-RAIM （novel integrity-optimized RAIM）算法［2］針對(duì)衛(wèi)星特征斜率提出最優(yōu)加權(quán)，可以有效地提升系統(tǒng)可用性，但會(huì)犧牲一定的定位精度，且復(fù)雜度較高，不易在側(cè)重定位域的實(shí)時(shí)接收機(jī)中使 用；廣 域 增 強(qiáng) 系 統(tǒng)（wide area augmentation system，WAAS）加權(quán)模型［3］的適用范圍較窄，僅限于GPS，不適用于多模多頻場(chǎng)景；雙頻加權(quán)模型［4］基于服務(wù)體積模型（service volume model，SVM），涵蓋了殘余電離層延遲、對(duì)流層延遲及多徑等主要誤差源，適用于GPS／Galileo雙模雙頻場(chǎng)景，但頻點(diǎn)間加權(quán)因子等權(quán)，帶來(lái)了一定的熱噪聲模型偏差.

傳統(tǒng)加權(quán)模型均未考慮信號(hào)體制對(duì)接收機(jī)熱噪聲的影響.在接收機(jī)偽碼跟蹤環(huán)路中，復(fù)合二進(jìn)制偏移載波（composite binary offset carrier，CBOC）、交替二進(jìn)制偏移載波（alternate binary offset carrier，AltBOC）等新型調(diào)制方式與二進(jìn)制相移鍵控（binary phase shift keying，BPSK）類(lèi)傳統(tǒng)調(diào)制方式的碼跟蹤精度不同.尤其在雙頻組合場(chǎng)景中，采用雙頻定位解算方法雖然能夠有效地抑制電離層延遲，但對(duì)各信號(hào)熱噪聲及多徑延遲有一定的放大作用，這將加大信號(hào)體制間觀測(cè)量的精度差距，造成測(cè)距觀測(cè)精度不等權(quán)現(xiàn)象.

傳統(tǒng)加權(quán)模型忽略了信號(hào)體制原因帶來(lái)的測(cè)距精度不等權(quán)問(wèn)題，該模型假設(shè)與實(shí)際不符的情況將對(duì)加權(quán)RAIM 技術(shù)性能的評(píng)估帶來(lái)偏差.本文在噪聲干擾層面，通過(guò)仿真分析了幾種典型信號(hào)在偽碼跟蹤延遲鎖相環(huán)路（delay-locked loop，DLL）跟蹤精度的差異性，根據(jù)信號(hào)調(diào)制方式、接收機(jī)設(shè)計(jì)參數(shù)和C／N0，建立新型接收機(jī)偽距誤差熱噪聲模型，推導(dǎo)了各頻點(diǎn)測(cè)距加權(quán)因子的產(chǎn)生方式，進(jìn)而細(xì)化完善了新型雙頻加權(quán)模型.仿真測(cè)試表明，該模型能夠更加合理地反映雙頻測(cè)距的實(shí)際噪聲，優(yōu)化了雙頻加權(quán)RAIM 算法的FDE 性能，提升了測(cè)距置信度水平并有效保證了定位精度，適用于不同信號(hào)體制共用的雙頻定位域場(chǎng)景.

1 信號(hào)體制對(duì)碼偽距測(cè)量精度的影響

1.1 多信號(hào)體制共用的現(xiàn)實(shí)趨勢(shì)

隨著信號(hào)結(jié)構(gòu)的設(shè)計(jì)與發(fā)展，出現(xiàn)了新一代信號(hào)體制，如在二進(jìn)制偏移載波（binary offset carrier，BOC）信號(hào)基礎(chǔ)上發(fā)展出的CBOC、AltBOC 等新型導(dǎo)航信號(hào)調(diào)制方式.新信號(hào)易于實(shí)現(xiàn)頻段資源復(fù)用、利于信號(hào)捕獲，具有降低偽碼跟蹤誤差、抑制信號(hào)多徑等顯著優(yōu)勢(shì)，已廣泛應(yīng)用于GNSS 各頻點(diǎn)中.傳統(tǒng)BPSK-R 信號(hào)將在導(dǎo)航系統(tǒng)中繼續(xù)使用，多種導(dǎo)航信號(hào)體制的共用與互操作已成為GNSS系統(tǒng)的現(xiàn)實(shí)應(yīng)用趨勢(shì).表1給出目前GNSS系統(tǒng)采用的主要信號(hào)調(diào)制方式.表中，BPSK-R（n）指具有（n ×1.023） MHz碼片速率的BPSK-R 信 號(hào)；BOC（a，b）指一個(gè)（a ×1.023） MHz的方波頻率與一個(gè)（b ×1.023） MHz碼片速率產(chǎn)生的BOC 調(diào)制信號(hào)；CBOC（6，1，1／11）信號(hào)是BOC（6，1）與BOC（1，1）通過(guò)時(shí)分復(fù)用方式，在導(dǎo)頻通道中按照1／10功率比組合而成；類(lèi)似地，BOC（6，1）與BOC（1，1）在時(shí)間復(fù)用二進(jìn)制偏置載波（time-multiplexed BOC，TMBOC）（6，1，4／33）信號(hào)導(dǎo)頻通道中的功率分配比是4／33.

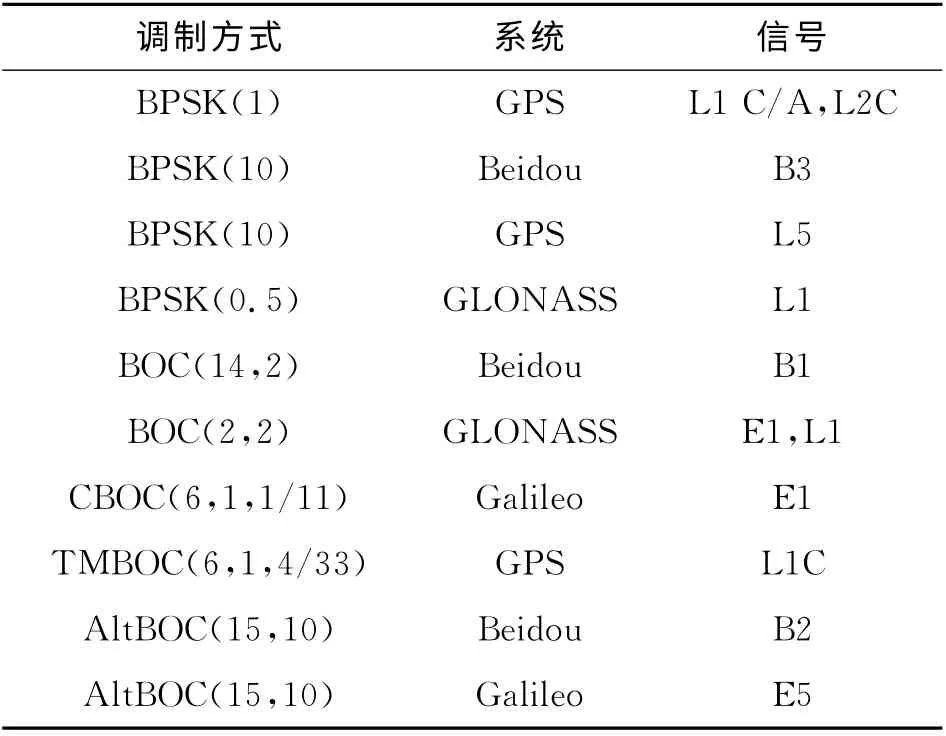
表1 GNSS廣泛采用的信號(hào)體制Tab.1 Widely adopted signal structures of GNSS

1.2 信號(hào)體制間碼跟蹤精度的差異性

為了分析不同信號(hào)體制在接收機(jī)碼環(huán)中的跟蹤精度，選取廣泛使用的BOC（14，2）、CBOC（6，1，1／11）、AltBOC（15，10）與BPSK-（1）、BPSK-（10）進(jìn)行分析.分析的跟蹤方法使用非相干超前和滯后（noncoherent early-late processing，NELP）算法.

根據(jù)碼跟蹤誤差理論估計(jì)理論［5-9］可知，信號(hào)通過(guò)DLL環(huán)路鑒別器后，輸出熱噪聲鑒別誤差方差為

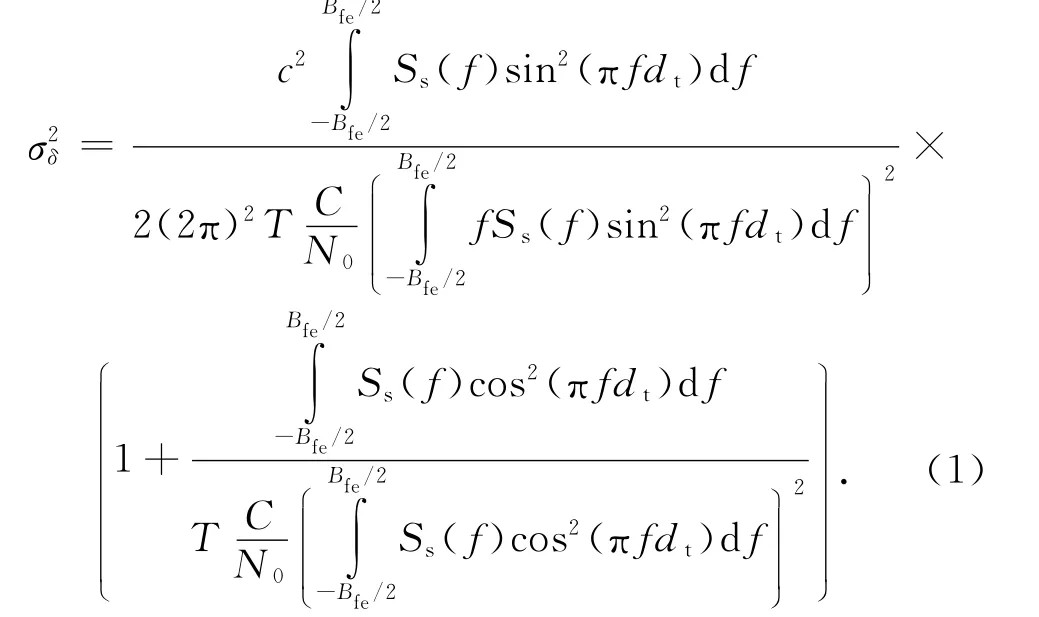
式中：c為光速，Bfe為接收機(jī)前端帶寬，Ss（f）為信號(hào)調(diào)制方式的歸一化功率譜密度，T 為預(yù)檢測(cè)積分時(shí)間，dt為相關(guān)器超前、滯后間隔.信號(hào)通過(guò)環(huán)路濾波器后，DLL環(huán)路碼跟蹤誤差σDLL為

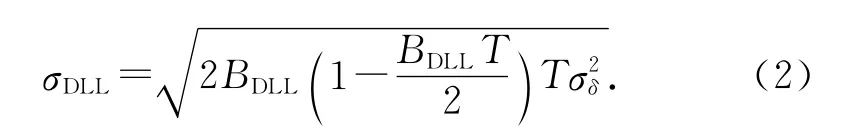
式中：BDLL為濾波器帶寬，σDLL為信號(hào)在單位測(cè)距標(biāo)準(zhǔn)差σ下的偽距測(cè)量精度.

σDLL與接收機(jī)設(shè)計(jì)參數(shù)相關(guān)，假設(shè)濾波器帶寬BDLL為5Hz，預(yù)檢測(cè)積分時(shí)間T 為20ms，AltBOC（15，10）前端帶寬為51 MHz，其余信號(hào)前端帶寬為18MHz.通過(guò)仿真得到各信號(hào)的碼環(huán)跟蹤誤差理論下限值，如圖1所示.可以看出，不同信號(hào)調(diào)制方式下的σDLL差別明顯，尤其在C／N0較低的弱信號(hào)條件下，40dB-Hz時(shí)BPSK-（1）的碼跟蹤誤差與其他調(diào)制信號(hào)相比已超出0.5m.

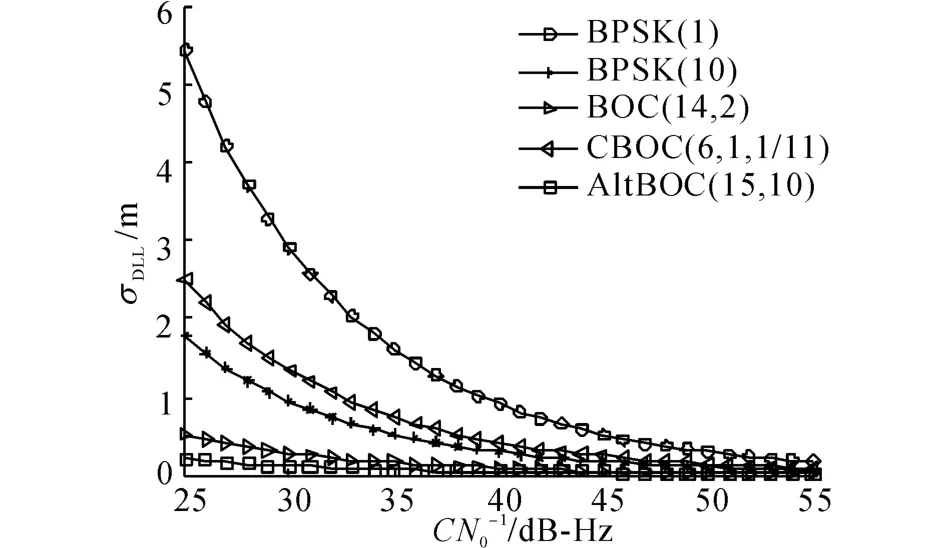
圖1 各信號(hào)的碼跟蹤誤差Fig.1 Code tracking error of signal structures

2 新型雙頻加權(quán)模型

通過(guò)處理捕獲信號(hào)的直接擴(kuò)頻序列，實(shí)現(xiàn)接收機(jī)碼片同步，進(jìn)而可以獲得偽距觀測(cè)值.碼偽距作為基本觀測(cè)量，置信度是影響PVT 定位精度的主要因素.理想測(cè)距為衛(wèi)星與用戶間的真實(shí)幾何距離，而實(shí)際測(cè)距含有噪聲誤差.一般地，測(cè)距噪聲服從期望為零、方差為σ2的高斯分布.噪聲方差越小，最終的定位結(jié)果越接近用戶的真實(shí)位置.測(cè)距噪聲方差是多種誤差方差的期望之和，可以表示為

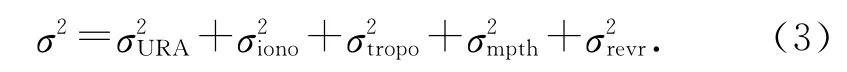
式中：σURA為星歷誤差，σiono為電離層延遲，σtropo為對(duì)流層 延 遲，σmpth為 多 徑 誤 差，σrevr為 接 收 機(jī) 熱 噪聲誤差.

2.1 傳統(tǒng)等權(quán)值雙頻模型

為了獲得更精確的定位解，可以通過(guò)2種方法抑制或部分消除噪聲的影響：一是通過(guò)算法或模型消除部分噪聲誤差；二是通過(guò)加權(quán)算法，以提高或降低測(cè)距權(quán)值的方式歸一化噪聲方差.在雙頻組合中，依靠頻點(diǎn)測(cè)距作差能夠消除大部分的電離層延遲，但熱噪聲屬于系統(tǒng)誤差，很難消除.在GPS／Galileo雙模雙頻場(chǎng)景中，傳統(tǒng)加權(quán)模型和各類(lèi)誤差方差模型［10-12］可以表示為

式中：測(cè) 距 間 用 戶 距 離 精 度（user range error，URA）可取1、0.5、0.2m；σ2L1L2為0.04，表示雙頻誤差參數(shù).對(duì)流層延遲模型σi，tropo為

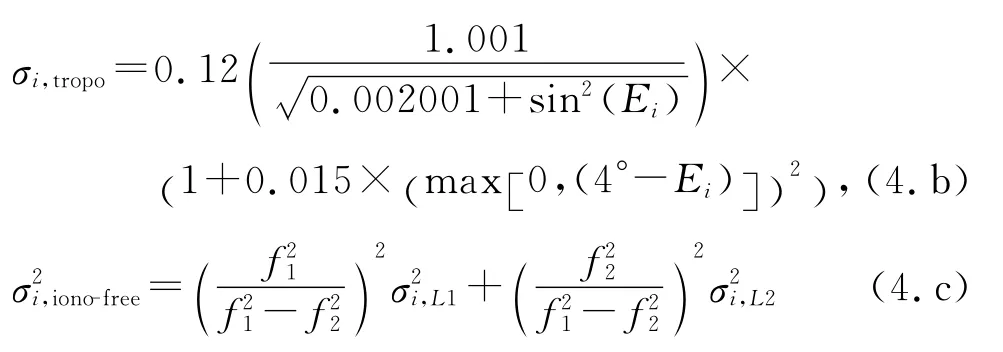
表示各頻點(diǎn)無(wú)電離層延遲模型，其中各頻點(diǎn)測(cè)距加權(quán)因子相等：

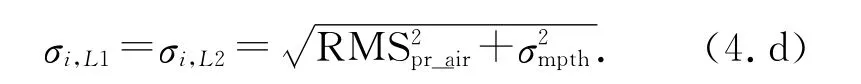
熱噪聲模型RMSpr-air與多徑延遲模型與仰角Ei相關(guān)：

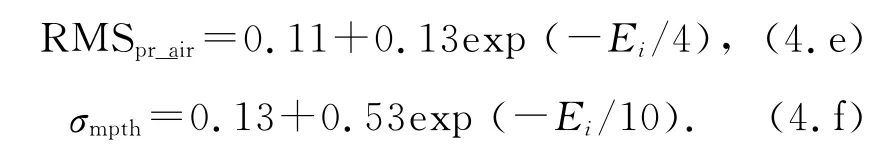
2.2 新型接收機(jī)偽距誤差熱噪聲模型

在雙頻組合的實(shí)際應(yīng)用中，一般可以假設(shè)URA誤差相等，由于頻點(diǎn)間信號(hào)經(jīng)過(guò)近似相同的對(duì)流層路徑，σtropo相等，σrevr及σmpth相互獨(dú)立.

根據(jù)1節(jié)的分析可知，不同信號(hào)體制下碼跟蹤誤差存在明顯差異，各頻點(diǎn)測(cè)距熱噪聲不等.由式（4.d）、（4.e）、（4.f）可知，傳統(tǒng)模型中熱噪聲方差RMSpr＿air與仰角相關(guān)，且假設(shè)各頻點(diǎn)測(cè)距σi，L1與σi，L2相等，這與接收機(jī)DLL環(huán)路熱噪聲的實(shí)際情況存在一定的偏差.傳統(tǒng)模型的頻率方差σ2L1L2為固定值，不能靈活地兼容各系統(tǒng)各頻點(diǎn)中心頻率不同的情況.

由于傳統(tǒng)模型不能兼顧不同調(diào)制方式組合使用的情況，尤其在如今新型信號(hào)和傳統(tǒng)信號(hào)共用與互操作廣泛應(yīng)用時(shí)期.為了改進(jìn)、修正傳統(tǒng)模型中接收機(jī)熱噪聲模型的偏差問(wèn)題，根據(jù)信號(hào)體制的差異性，由式（1）、（2）可得基于信號(hào)體制的新型熱噪聲方差模型：

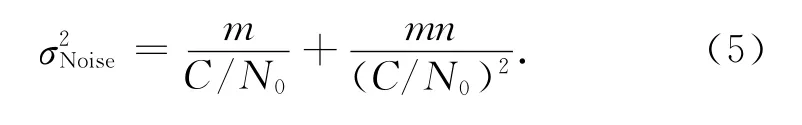
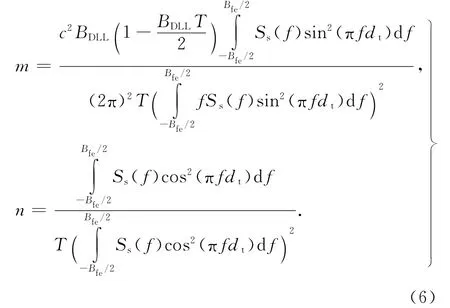
新型熱噪聲模型與信號(hào)體制功率譜密度、接收機(jī)碼環(huán)設(shè)計(jì)參數(shù)及C／N0相關(guān)，將該模型替換傳統(tǒng)模型中的RMS2pr＿air與σ2L1L2項(xiàng)，各頻點(diǎn)測(cè)距的加權(quán)因子σ′i為

2.3 新型雙頻加權(quán)模型描述

雙頻組合能夠消除大部分電離層誤差，無(wú)電離層偽距ρi 的數(shù)學(xué)模型［13］為

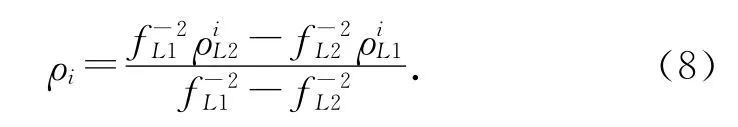
式中：f1、f2為各頻點(diǎn)的中心頻率，ρL1、ρL2為各頻點(diǎn)的偽距.對(duì)式（8）求期望后，可得雙頻加權(quán)方差為

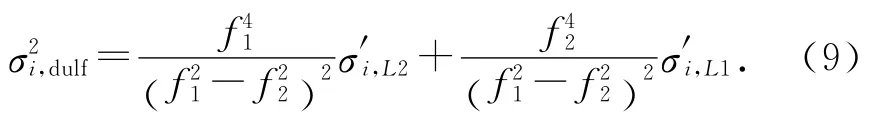
由式（9）可見(jiàn)，雙頻組合將增大接收機(jī)熱噪聲和多徑誤差.當(dāng)σ′i，L1與σ′i，L2一定時(shí)，2個(gè)頻率的間隔越大，對(duì)誤差的放大作用越小；當(dāng)2個(gè)頻點(diǎn)的偽距跟蹤精度不同時(shí)，高頻頻點(diǎn)測(cè)距誤差所占的比重更大.

綜上所述，基于信號(hào)體制優(yōu)化的雙頻加權(quán)模型為

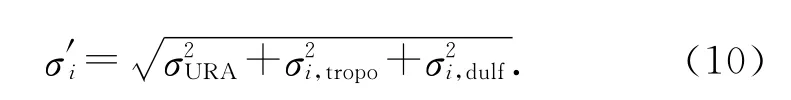
σURA使用傳統(tǒng)估計(jì)值.

3 新模型對(duì)RAIM 技術(shù)的影響

新型雙頻模型作為一項(xiàng)基礎(chǔ)模型，可以廣泛應(yīng)用于加權(quán)定位估計(jì)與加權(quán)RAIM 技術(shù).

根據(jù)加權(quán)最小二乘定位解算模型可知，加權(quán)最小二乘估計(jì)解［11］為

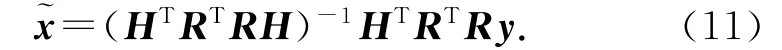
式中：R 為歸一化噪聲方差加權(quán)矩陣，

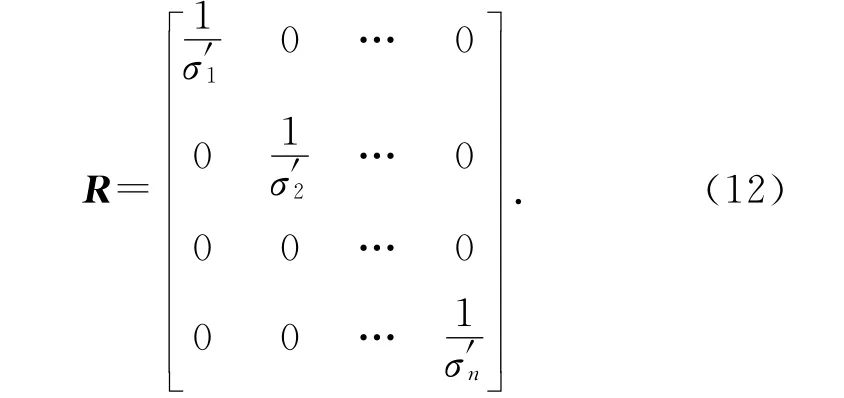
加權(quán)矩陣實(shí)現(xiàn)了測(cè)距誤差的歸一化處理.由式（11）可得歸一化的偽距殘差矢量w 與映射矩陣U：

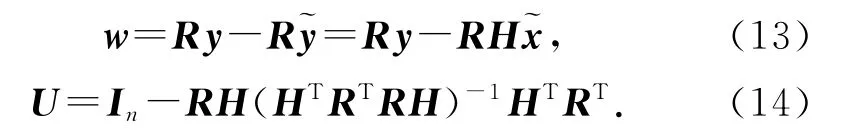
w 各分量相互獨(dú)立，可得w＝URy＝URn，其中n 為噪聲矢量，服從期望為0、方差為1的高斯分布.由于w 的幅值體現(xiàn)了觀測(cè)值間的一致性，可將歸一化的偽距殘差平方和作為檢驗(yàn)統(tǒng)計(jì)量［14］，雙模條件下服從自由度為（n-5）的χ2分布.根據(jù)用戶給定的虛警率Pfa能夠確定歸一化的檢驗(yàn)門(mén)限值T，進(jìn)而判決測(cè)距是否存在粗差.

4 仿真驗(yàn)證與分析

通過(guò)仿真得到GPS24 星星座及Galileo27／3／1Walker星座，仰角遮蔽角為5°，時(shí)長(zhǎng)1d，采樣步長(zhǎng)為1min，獲得1 440個(gè)采樣點(diǎn).以5°×5°為采樣區(qū)間，遍歷得到全球范圍可見(jiàn)衛(wèi)星數(shù)的分布情況，如圖2所示.圖中，SatN為可見(jiàn)衛(wèi)星數(shù)，Pr為分布概率.

按照航空無(wú)線電委員會(huì)（Radio Technical Commission for Aeronautics，RTCA）規(guī)定的“最小操作性能標(biāo)準(zhǔn)”［15］要求，遍歷全球24個(gè)地點(diǎn).測(cè)距標(biāo)準(zhǔn)差σ統(tǒng)一取2.5m，URA 取1m，Pfa取0.01.假設(shè)各系統(tǒng)雙頻組合為：GPS L1 C／A 碼BPSK-R（1），中心頻點(diǎn)頻率為1 575.42 MHz，L5BPSK-R（10），中心頻點(diǎn)頻率為1 176.45 MHz；Galileo E1 CBOC（6，1，1／11），中心頻點(diǎn)為1 575.42 MHz，E5a AltBOC（15，10），中心頻點(diǎn)為1 191.795 MHz.

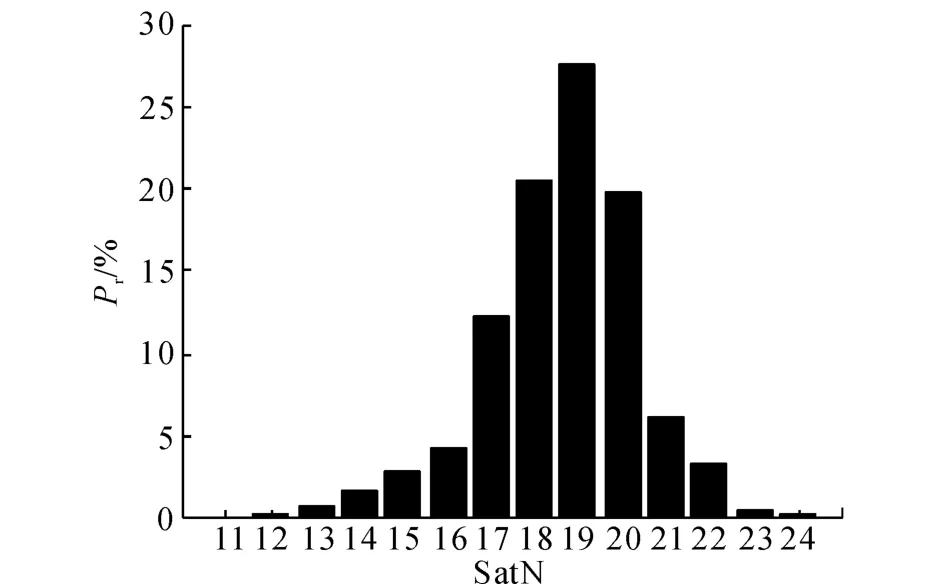
圖2 可見(jiàn)衛(wèi)星數(shù)分布Fig.2 Distribution of number of visible satellites

為了仿真對(duì)比各模型對(duì)全球RAIM 技術(shù)FDE平均性能的影響.設(shè)置3種處理方法，方法a為單頻處理方法，方法b為雙頻等權(quán)處理方法，方法c為本文提出方法.由于雙模或多模場(chǎng)景的漏檢率極低［16］，考慮故障檢測(cè)率和虛警率指標(biāo).為了便于直觀顯示，在虛警量級(jí)接近的條件下，對(duì)新模型與傳統(tǒng)模型進(jìn)行比較.表2給出各場(chǎng)景3～10σ的全球24地點(diǎn)的平均FDE 性能.單頻方法的故障檢測(cè)率較低，虛警率極低.雙頻方法的故障檢測(cè)率大幅高于單頻方法，本文方法優(yōu)化了加權(quán)RAIM 技術(shù)的FDE性能，c方法的故障檢測(cè)率優(yōu)于b方法，尤其在故障較小時(shí)更加顯著.

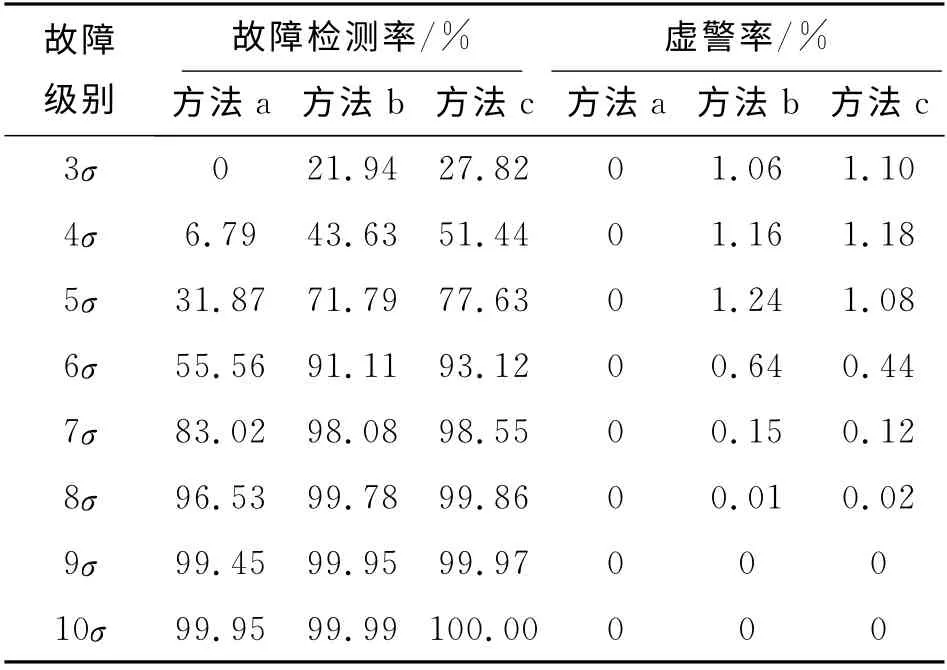
表2 平均FDE性能Tab.2 Average FDE performance

在上述仿真環(huán)境下，經(jīng)過(guò)FDE 步驟，分析各方法的定位精度.選擇北京觀測(cè)站，隨機(jī)選取一個(gè)健康衛(wèi)星，在觀測(cè)測(cè)距的各個(gè)采樣歷元中均加入±5 m至±25m 的隨機(jī)突變偏差，得到圖3所示的各場(chǎng)景定位 精 度，三 維 均 方 根 誤 差（root mean square，RMS）列于圖3的右下角.圖中，Lat為緯度，Lng為經(jīng)度.由于故障檢測(cè)率較低，含故障偏差測(cè)距影響了觀測(cè)測(cè)距置信度，方法1的RMS較高，為4.41m；方法2的RMS為3.37m；經(jīng)過(guò)本文提出模型的進(jìn)一步優(yōu)化，方法3的RMS降至2.96m，與雙頻等權(quán)方法相比，定位精度提升約0.4 m.需要指出，方法2、3是經(jīng)過(guò)RAIM 故障檢測(cè)與排除，獲得較高測(cè)距置信度，并對(duì)測(cè)距噪聲歸一化加權(quán)定位解算共同優(yōu)化的結(jié)果.

為了不失一般性，表3給出各方法在全球24地點(diǎn)的平均RMS結(jié)果.各方法的定位精度與北京觀測(cè)站定位精度相近，可以看出，采用本文模型可以有效地保證定位精度.

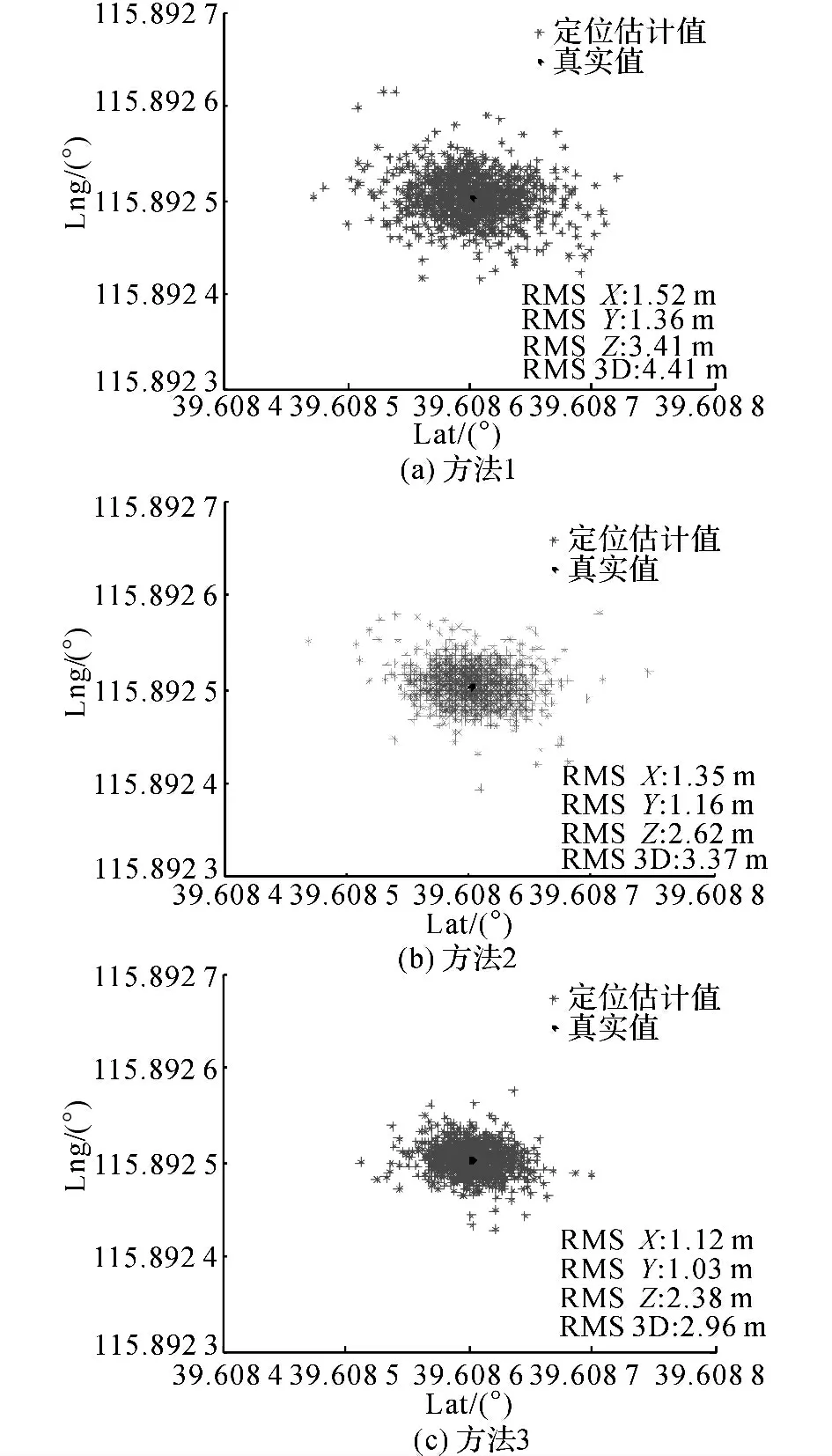
圖3 方法1～3的定位精度Fig.3 Positioning accuracy of method 1～3

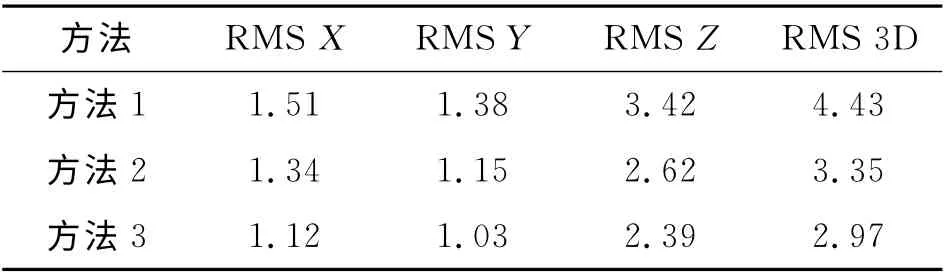
表3 全球24地點(diǎn)平均RMSTab.3 Average RMS of 24worldwide locations m

5 結(jié) 語(yǔ)

本文在分析幾種典型信號(hào)調(diào)制方式在接收機(jī)DLL環(huán)路碼跟蹤精度的基礎(chǔ)上，提出基于信號(hào)體制的接收機(jī)熱噪聲加權(quán)模型.結(jié)合傳統(tǒng)雙頻組合各噪聲方差估計(jì)，分析新模型對(duì)雙頻加權(quán)RAIM 技術(shù)性能及定位估計(jì)精度的影響.仿真測(cè)試表明，采用本文模型能夠優(yōu)化提高RAIM 技術(shù)FDE 性能，提升各頻點(diǎn)測(cè)距置信度水平，并有效地保證定位精度，適合于信號(hào)體制共用條件下的定位域應(yīng)用場(chǎng)景.作為基礎(chǔ)加權(quán)模型，該模型能夠適應(yīng)信號(hào)體制多樣化的展趨勢(shì)，具有廣泛適用性的特點(diǎn).

（

）：

［1］郭婧.多模多頻衛(wèi)星導(dǎo)航系統(tǒng)RAIM 技術(shù)研究［D］.北京：清華大學(xué)，2011：1-12.GUO Jing.Research on RAIM for multi-constellation and multi-frequency satellite navigation systems ［D］.Beijing：Tsinghua University，2011：1-12.

［2］MADONNA P，VIOLA S，SFARZO L.NIORAIM algorithm applied to a multiconstellation GNSS：analysis of integrity monitoring performances in various phases of flight［C］∥Position Location and Navigation Symposium（PLANS）.Palm Springs：IEEE，2010：1258-1263.

［3］WALTER T，ENGE P.Weighted RAIM for precision approach［C］∥ION GPS 1995.Palm Springs：［s.n.］，1995：1995-2004.

［4］HARTINGER H，BRUNNER F K.Variances of GPS phase observations：the SIGMA-εmodel［J］.GPS Solutions，1999，2（4）：35-43.

［5］BETZ J W，KOLODZIEJSKI K R.Generalized theory of code tracking with an early-late discriminator Part I：lower bound and coherent processing［J］.IEEE Transactions on Aerospace and Electronic Systems，2009，45（4）：1538-1550.

［6］BETZ J W，KOLODZIEJSKI K R.Generalized theory of code tracking with an early-late discriminator part II：noncoherent processing and numerical results［J］.IEEE Transactions on Aerospace and Electronic Systems，2009，45（4）：1557-1564.

［7］何在民.衛(wèi)星導(dǎo)航信號(hào)碼跟蹤精度研究［D］.北京：中國(guó)科學(xué)院研究生院，2012：35-43.HE Zai-min.Research on code tracking accuracy for satellite navigation signals［D］.Beijing：Chinese Academy of Sciences，2012：35-43.

［8］LIU A，AN J，WANG A.Effect of transform domain interference suppression on PN code tracking loops［C］∥2010 12th IEEE International Conference on Communication Technology.Nanjing：IEEE，2010：1064-1067.

［9］LIU Y，RAN Y，KE T，et al.Code tracking performance analysis of GNSS signal in the presence of CW interference［J］.Signal Processing，2011，91（4）：970-987.

［10］RTCA DO-229D，Minimum operational performance standards for global positioning system／wide area augmentation system airborne equipment［S］.Washington，DC：RTCA，2006.

［11］KAPLAN E D，HEGARTY C J.GPS 原 理 與 應(yīng) 用［M］.寇艷紅，譯.北京：電子工業(yè)出版社，2012：258-265.

［12］LEE Y，BRAFF R，F(xiàn)ERNOW J，et al.GPS and Galileo with RAIM or WAAS for vertically guided approaches［C］∥Proceedings of the Institute of Navigation GNSS.Long Beach：Institute of Navigation，2005：1801-1825.

［13］劉家興.衛(wèi)星定位精度和自主完好性的改進(jìn)［D］.北京：清華大學(xué)，2008：25-27.LIU Jia-xing.Improvement of satellite positioning sccuracy and sutonomous integrity［D］.Beijing：Tsinghua University，2008：25-27.

［14］代長(zhǎng)勇，常青，陳媛.多系統(tǒng)衛(wèi)星導(dǎo)航接收機(jī)自主完好性監(jiān)測(cè)［J］.遙測(cè)遙控，2010，31（6）：11-15.DAI Chang-yong， CHANG Qing， CHEN Yuan.Multi-system satellite navigation receiver autonomous integrity monitoring［J］.Journal of Telemetry，Tracking and Command，2010，31（6）：11-15.

［15］RTCA DO-229D，Minimum operational performance standards for airborne supplemental navigation equipment using global positioning system （GPS）.Washington，DC：RTCA，1991.

［16］許龍霞，張慧君，李孝輝.多模衛(wèi)星導(dǎo)航系統(tǒng)的RAIM算法研究［J］.時(shí)間頻率學(xué)報(bào)，2011，34（2）：131-138.XU Long-xia，ZHANG Hui-jun，LI Xiao-hui.Study on RAIM algorithm of multi-mode navigation system ［J］.Journal of Time and Frequency，2011，34（2）：131-138.