運輸問題的對偶模型
吳振華王亞蓓
(1.桂林電子科技大學商學院,廣西 桂林 541004;2.桂林電子科技大學信息科技學院,廣西 桂林 541004)
運輸問題的對偶模型
吳振華1王亞蓓2
(1.桂林電子科技大學商學院,廣西 桂林 541004;2.桂林電子科技大學信息科技學院,廣西 桂林 541004)
線性規劃原問題與對偶模型之間的轉化方法一直是普通高校經營類本科生《運籌學》課程的教學重點。運輸問題是線性規劃中的一類典型問題,其屬于非常規線性規劃模型,掌握運輸問題原模型與對偶模型之間的轉化過程對于學習后續相關內容極為重要。文章首先推導出“常規”與“非常規”線性規劃問題模型的對偶形式,然后總結線性規劃模型與對偶問題模型的對應關系,最后舉例說明運輸問題模型的對偶形式。
線性規劃;運輸問題;對偶模型
《運籌學》是普通高校經營類本科生的基礎必修課,對偶規劃則是線性規劃問題中的重要內容,也是教學難點。對偶模型的提出以及模型轉化問題是學習對偶性質(定理)的重要基礎,但在已有教材中只是直接給出線性規劃及對偶模型的對應關系,較少對偶形式轉化的推導過程進行詳細說明,因此學生在自學時往往感覺力不從心。運輸問題模型屬于非常規線性規劃問題模型,具有“目標函數求最小值”、“約束條件為等式”等特點,如果不能熟練掌握原問題與對偶問題模型的轉化方法,難以迅速寫出其對偶模型。為此,本文詳細介紹線性規劃原問題與對偶問題模型的推導過程,總結兩者的對應關系,舉例說明運輸問題模型的轉化過程,為深刻理解對偶規劃內容以及學習相關內容提供參考。
1 運輸問題及模型
運輸問題是指在某時期內將供應地的某類物資,分別運到需要這些物資的地區,在已知各地供應量和需要量及各地之間的單位運輸費用時,制定總運輸費用最小的調運方案。例如,有三個產糧區A1、A2、A3,可供糧食為10、8、5,將糧食運往B1、B2、B3、B4四個地區,需求量分別為5、7、8、3。產糧地到需求地的單位運價如表1所示,問如何安排才能使總的運輸費用最少[1]?
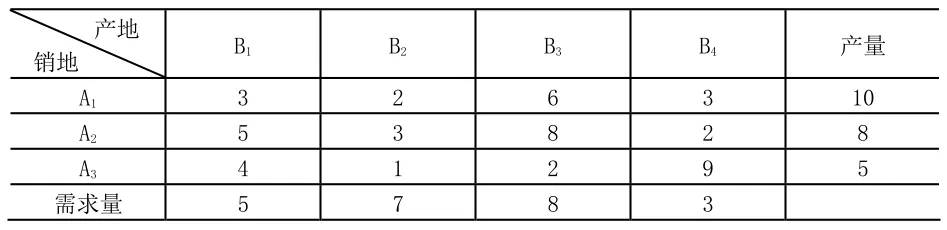
表1 產糧地到需求地的單位運價
這是一個典型的產銷平衡運輸問題,已知每條運輸路線的單位運價,為獲得總的運輸費用,需要確定每條運輸路線的運輸量,因此可設xij(i =1,2,3;j =1,2,3,4)為i個產糧地運往第j個需求地的運輸量,如表2所示,則該問題的目標函數為:min S =3x11+ 2x12+ 6x13+ 3x14+ 5x21+ 3x22+8x23+ 2x24+ 4x31+ x32+ 2x33+ 9x34。
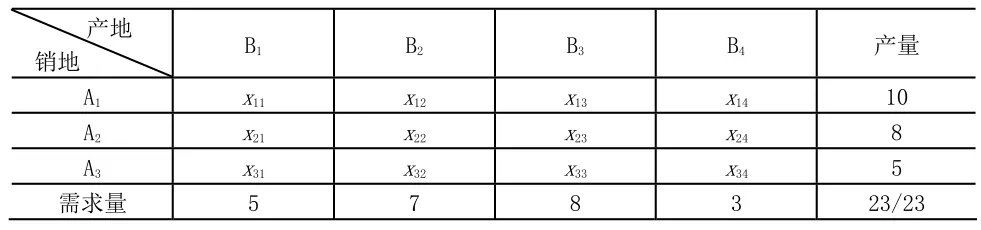
表2 產糧地運往需求地的運輸量
根據題意,每個產地的產量都要運到各個需求地,因此有如下等式成立:x11+ x12+ x13+ x14= 10;x21+ x22+ x23+ x24= 8;x31+ x32+ x33+ x34= 5。同時,每個需求地的需求量均得到滿足,因此有如下等式成立:x11+ x21+ x31= 5;x12+ x22+ x32= 7;x13+ x23+ x33= 8;x14+ x24+ x34= 3。另外,從第i個產糧地運往第j個需求地的運輸量均為非負。綜上,得到該運輸問題的數學模型(1):
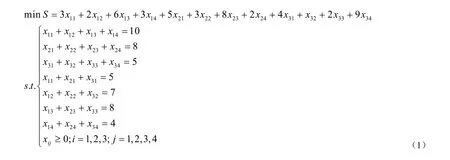
一般而言,對于產銷平衡運輸問題,通常設xij( i =1, 2, …, m;j=1, 2, …, n)為第i個產地到第j個銷地的運量,則數學模型為:
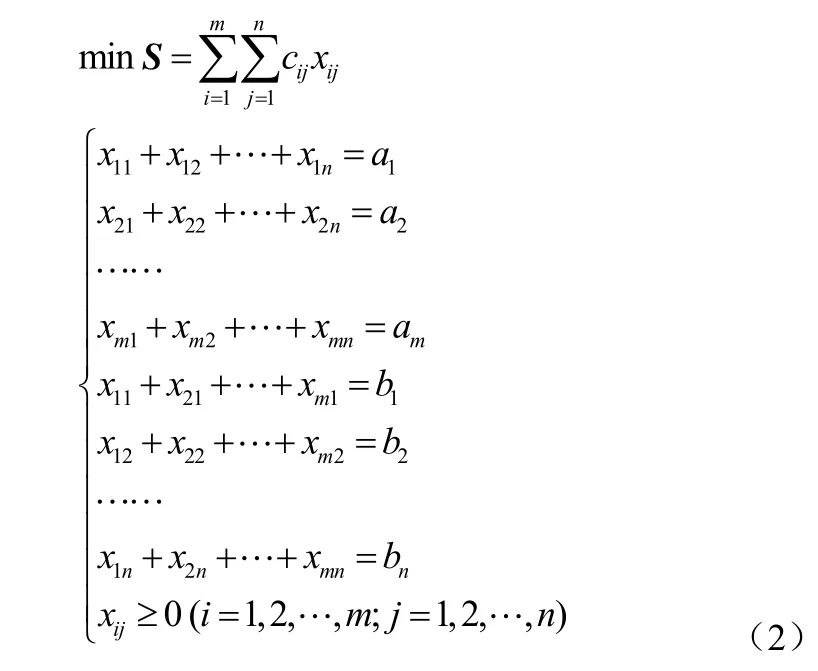
模型(2)可簡寫為:
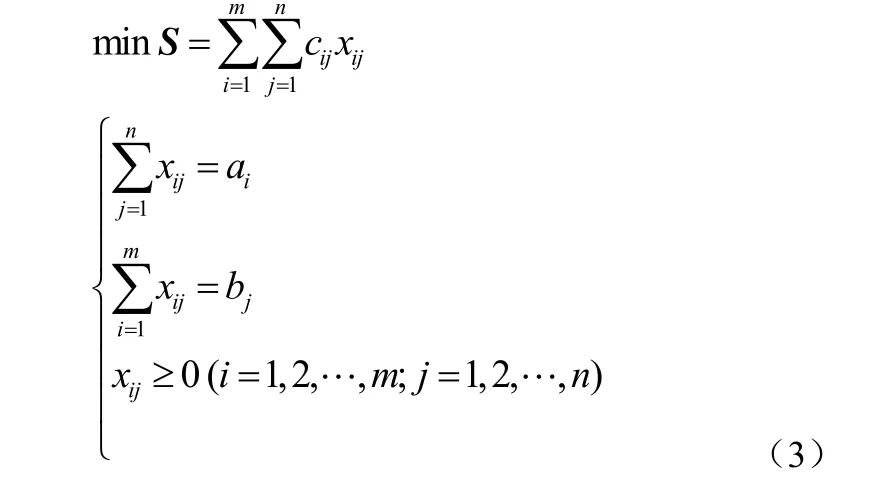
2 原問題與對偶問題模型
2.1 常規模型
原問題數學模型可用矩陣形式(4)表達。

若原問題具有最優解,其檢驗數必定小于等于零,即σ ≤0或C - CBB-1A ≤ 0。令Y=CBB-1,則有不等式C -YA≤ 0或YA ≥C成立。由于松馳變量XS對應價格向量CS= 0,則有不等式σS= CS- CBB-1I ≤ 0或CBB-1≥ 0(即Y ≥0)成立。同時,希望資源價格Y和數量b的乘積越小越好,即minW =Yb,則對偶問題數學模型為(5,本文稱模型(4)和(5)為常規形式。

2.2 非常規模型
2.2.1 約束條件為等式
原問題模型為:
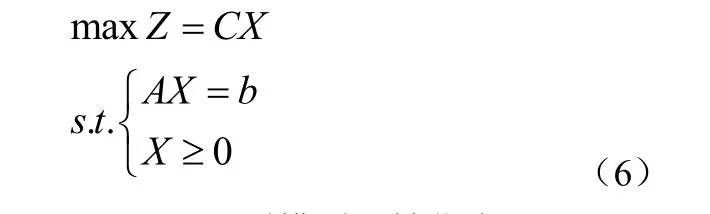
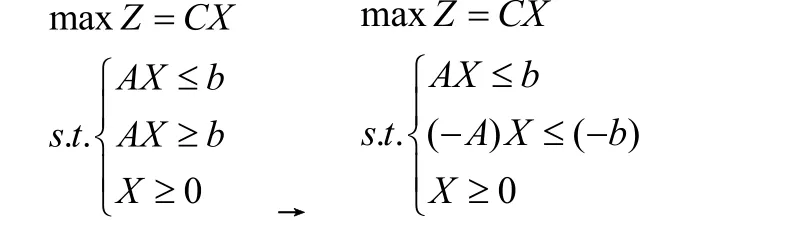
根據模型(4)和(5)可轉化為對偶形式,過程如下:
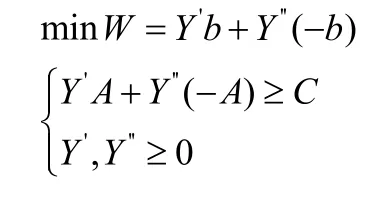
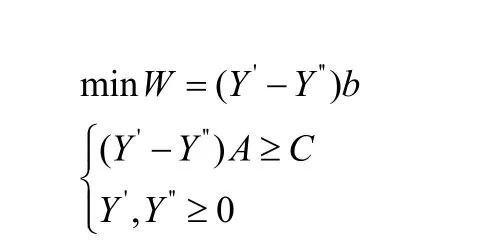
最終得到非常規線性規劃問題的對偶模型(7):

2.2.2 決策變量取值無約束
令X = X′-X",模型(8)可轉化為模型(9)。
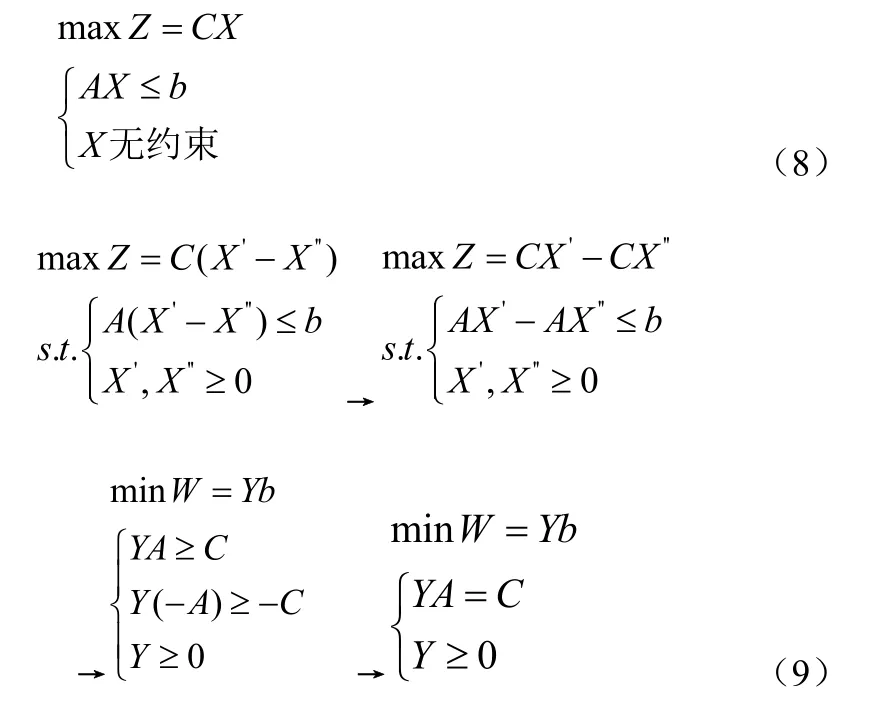
通過對常規和非常規對偶模型的推導,可得出原問題與對偶問題模型的對應關系,如表3所示。
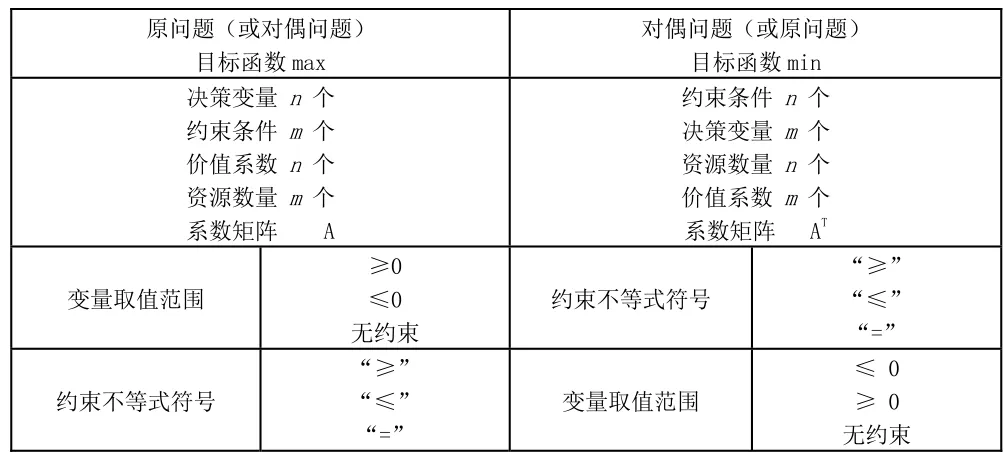
表3 原問題與對偶問題模型要素對應表[2][3]
3 運輸問題模型的對偶形式
已知某運輸問題模型(10),試求其對偶問題模型[4]?
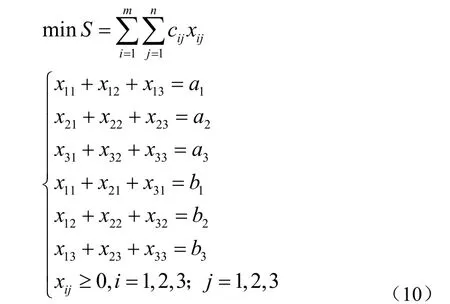
由于原問題約束條件個數為6,因此可設對偶變量分別為u1、u2、u3、v1、v2和v3,即Y = (u1, u2, u3, v1, v2, v3),同時,b = (a1, a2, a3, b1, b2, b3)T,對偶問題目標函數為:
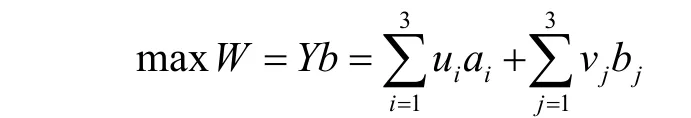
原問題模型中系數矩陣為:

因此,YA = (u1+ v1, u1+ v2, u1+ v3, u2+ v1, u2+ v2, u2+ v3, u3+ v1, u3+ v2, u3+ v3)T= ui+ vj,簡寫為:YA = ui+ vj(i = 1,2,3; j = 1,2,3)。同時,YA ≤ C,具體為:u1+ v1≤ c11,u1+ v2≤ c12,u1+ v3≤ c13,u2+ v1≤ c21,u2+ v2≤ c22,u2+ v3≤ c23,u3+ v1≤ c31,u3+ v2≤ c32和u3+ v3≤c33,可簡寫為:ui+ vj≤ cij。綜上,該運輸問題模型的對偶形式為:
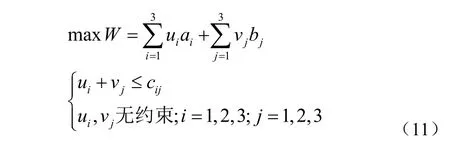
4 教學體會
了解“常規”和“非常規”線性規劃問題與對偶問題的模型轉化過程,有助于理解模型之間決策變量與約束條件之間的對應關系,為學習對偶性質(定理)及后續內容提供幫助,例如,在掌握運輸問題對偶模型之后,學習表上作業法中的檢驗方法—位勢變量法時會倍感輕松。然而,在教學過程中發現,許多學生對表3的記憶和使用仍然存在著一定的困難。為此提出以下建議:首先,選擇兩道典型習題,應含以下信息:目標函數求max和min,約束條件中不等式符號有“≥”、“≤”和“=”,決策變量取值范圍有“≥0”、“≤0”和“取值無約束”;然后,參照表3將原問題模型轉化成對偶形式,再以對偶模型為原問題進行轉化,只需重復兩遍就能牢牢記住轉化過程,切忌死記硬背。
[1] 吳振華.運籌學[M].北京:北京理工大學出版社,2014.
[2] 謝家平.管理運籌學[M].北京:中國人民大學出版社,2010.
[3] 常大勇.運籌學[M].北京:中國物資出版社,2010.
[4] 熊偉.運籌學[M].北京:機械工業出版社,2005.
Dual model transport problem
The problem with the original linear programming method for converting between the dual model has been the focus of ordinary business class teaching undergraduate colleges "Operations Research" course. Transportation is a linear programming problem in a class of typical problems, their unconventional linear programming model, master transportation problem with the original model of the transformation process between the dual model is extremely important for the study follow-up related content. This paper deduced the "General" and "unconventional" linear programming problem model dual form, and then summarize the correspondence between linear programming model with the dual problem of the model, and finally illustrate the dual form of transportation problem model.
linear programming; transportation issues; dual model
E83
A
1008-1151(2015)03-0150-03
2015-02-12
廣西壯族自治區教育廳資助“工業工程特色專業及課程一體化建設項目”(GXTSZY212)。
吳振華(1972-),男,河北樂亭人,桂林電子科技大學商學院副教授,博士,碩士生導師,研究方向為房地產經濟、城市土地增值與收益分配、工業工程與管理。

