開口環變形分析

姚本春，丁慶新，侯　越，張仕民（中國石油大學（北京）機械與儲運工程學院，北京102249）

開口環變形分析

姚本春，丁慶新，侯越，張仕民
（中國石油大學（北京）機械與儲運工程學院，北京102249）

對水平井壓裂滑套中使用的開口環在壓縮、閉合過程中的變形進行了分析。根據試驗中開口環與壓套之間的接觸面變形情況提出了變形過程中的局部接觸假設，結合能量法建立了開口環變形過程的力學模型，給出了局部接觸力和開口角度之間的函數關系。用ABAQUS軟件對開口環的變形過程進行分析，分析的結果與力學模型計算結果較好地吻合，證實了局部接觸假設的有效性和力學模型的準確性。

開口環；卡簧；滑套；能量法

開口環是機械工業常用的撓性零部件之一，在外力的作用下可發生彈性變形，取消外力后又可恢復到原來的狀態。具有結構簡單、安裝方便的特點，廣泛應用在軸系零部件的軸向定位與固定、管道快速接頭等場合［1-3］。

開口環的結構和尺寸參數對連接的強度和可靠性有重要的影響。諸多文獻對開口環在變形過程中的載荷進行了相關的研究，楊進等人用有限元軟件ANSYS研究了SR30型快速接頭卡簧端面角度、接頭有效搭接長度及材質與接頭結構極限抗彎承載力的關系［4］；郝忠獻等人在井下壓裂滑套中使用卡簧對滑閥進行軸向定位，分析了卡簧越過軸套臺肩時的軸向力［5］；周俊超等人在水溫的影響下對水管接頭進行了非線性接觸分析［6］；溫紀宏根據用莫爾定理建立了快速接頭中的卡簧受壓縮過程的力學模型［7］；從偉等人建立了卡簧切口張開量與結構尺寸之間的數學方程，并給出了特定方向載荷作用下卡簧的張開量［8］。

本文將開口環應用在一種新型的水平井壓裂滑套中，該滑套利用開口環受壓縮變形后內徑減小的特性選擇性地開啟某一特定的滑套。該滑套與開口環油管部分的結構如圖1所示（該視圖為沿對稱面剖開的半剖視圖），開口環位于壓套和擋套之間，開口環的外徑上有坡口，坡口的角度與壓套內錐面的角度相匹配。初始時，開口環通過坡口與壓套接觸，開口環的底端與擋套的上端面接觸；工作過程中，擋套固定不動，對開口環有著軸向限位的作用。開口環的自然狀態內徑較大，允許壓裂球從中自由通過，但要開啟特定的滑套時，外部機構會推動壓套沿著軸向運動，從而擠壓開口環使其開口角度減小。最終，開口環完全閉合，形成一個完整的球座。閉合后的開口環內徑小于壓裂球的直徑，待壓裂球入座后，在泵壓的作用下打開滑套。

開口環閉合所需的軸向力是壓套驅動機構設計的主要依據。將開口環擠壓變形過程進行適當簡化，建立開口環坡口與壓套內錐面之間的接觸力數學模型，通過接觸區域的幾何角度，將接觸力轉化成作用在壓套上的軸向力。用有限元分析軟件ABAQUS建立計算模型，求得開口環變形過程中對壓套的軸向力，并將理論模型和有限元方法計算所得的軸向力進行對比分析。

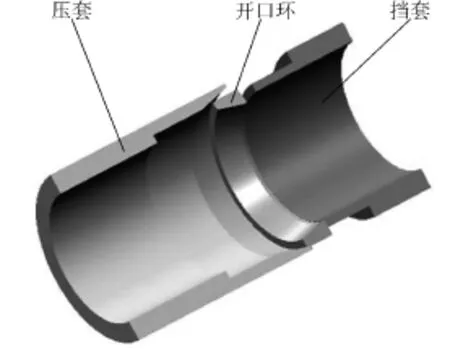
圖1　工具結構示意

1　開口環變形過程數學模型

1.1簡化與假設

已有文獻中，將開口環與內錐面之間相互作用力簡化成在開口環外圈上的分布載荷［4，7］。但是，從試驗結果來看，開口環的外圈并不是總和壓套內表面接觸，而是更傾向于在開口處產生較大的集中力。如圖2a所示，開口處的集中力在壓套的內錐面上留下了較為明顯的劃傷，說明此處有較大的集中力，而遠離開口環的在開口的接觸區，開口環基本上不與壁面接觸。在有限元計算的結果中，某一時刻開口環上的應力分布如圖2b所示，開口環的內表面上產生了較大的應力，這與開口端集中力產生的應力分布情況較為類似。

根據試驗現象和有限元計算的結果，并為了簡化計算，提出以下假設：

1）開口環的外壁和壓套的內壁之間的相互作用等效為作用在開口端的集中力。

2）開口環上存在中性軸，在變形過程中，中性軸的長度保持不變。

3）根據圣維南原理，作用在外表面上的力等效為作用在端面中性軸上的力。

表3為不同組別老齡人太極拳鍛煉過程中左右側骨骼肌IEMG相關系數。對照組左右側下肢脛骨前肌、股外側肌、臀大肌相關系數顯著，實驗組腓腸肌、脛骨前肌、股直肌、股內側肌、臀大肌、股二頭肌相關系數顯著。

4）開口環的兩臂在變形過程中保持形狀為圓弧形。

圖2　試驗和有限元仿真

開口環的簡化變形過程如圖3所示。開口環在變形過程中保持對稱性，以左半邊為研究對象。開口環的曲率中心在O0點，初始開口角度為α0，中性軸上的弦長為δ0，中性軸的半徑為R0，作用在左端開口處的集中力為F0。在變形過程中的某一個狀態，開口環的曲率中心偏移至O點，開口環的開口角度為α，中性軸上的弦長為δ，中性軸的半徑為R，集中力為F。開口環的底端受到壓套內表面的限位，該處截面位置始終保持不變，開口環上其他任意一個截面的角位置用φ表示。

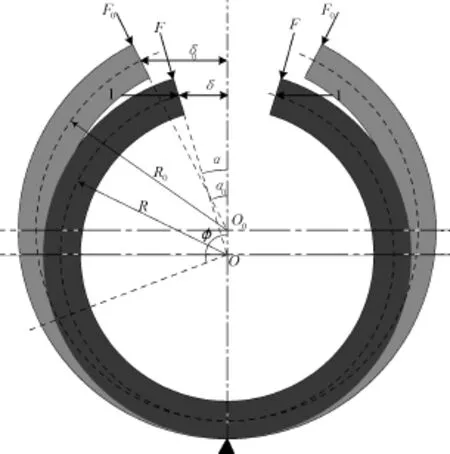
圖3　開口環變形示意

1.2數學模型

用能量法中的虛功原理建立開口環變形過程的數學模型。平衡外力系選為作用在開口端中性軸上的一對水平單位集中力，F作用下產生的變形為虛變形，則單位力的虛功為

We=1·（δ0-δ）（1）

由中性軸假設得：

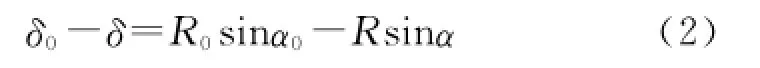
單位力引起的內力在虛變形上做的功為

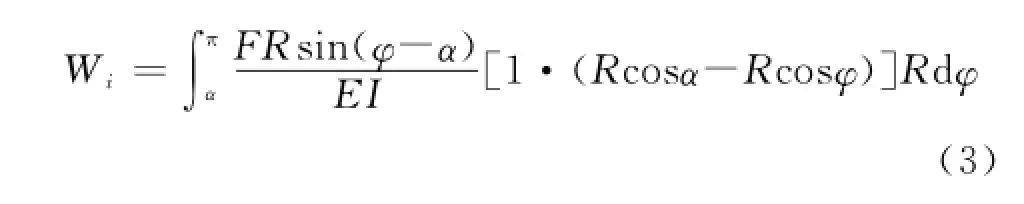
式中：I為截面相對于中性軸的慣性矩；E為材料的彈性模量。

We=Wi（4）

由式（1）～（4）得：

開口環截面為不規則形狀，中性軸的位置不能精確計算，由于截面的尺寸與開口環的內外徑相差較大，式（5）對初始時刻中性軸的位置不敏感，簡化計算時，可將中性軸取在內外徑的中間。截面的慣性矩對中性軸在截面上的位置比較敏感，需根據具體的變形情況給定。

2　有限元模擬

開口環與壓套和擋套之間存在著相對滑動的接觸面，零件的幾何形狀也是不連續的，同時，開口環從壓套的內錐面進入到圓柱面內是產生較大的位移和變形。有限元分析軟件ABAQUS適合分析這類大變形和非線性的接觸問題。

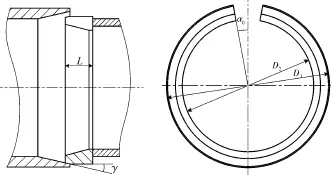
圖4　工具的幾何形狀

2.1幾何模型

工具的幾何形狀和幾何尺寸如圖4和表1所示。

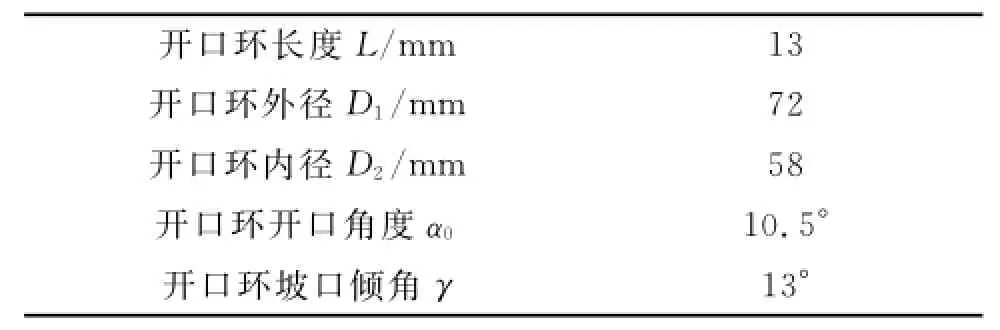
表1　幾何尺寸

2.2ABAQUS軟件設置

在開口環和壓套的對稱面上施加對稱約束，擋套底端施加固定約束。開口環的坡口和壓套的內錐面之間建立接觸關系，開口環的底面和擋套的接觸面之間建立接觸關系。材料選用45鋼，接觸面之間的摩擦因數為0.2。給定壓套20mm的位移，開口環從初始位置發生變形，最后彎曲進入到壓套的內柱面中，整個過程中，驅動壓套所需的軸向力隨時間的變化曲線如圖5所示。

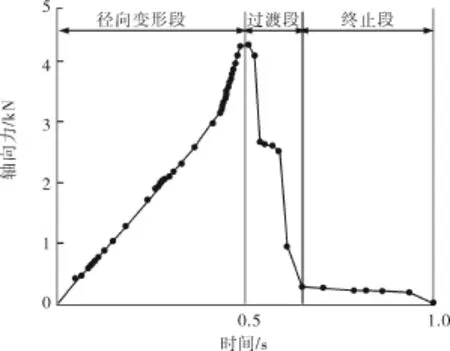
圖5　軸向力隨時間的變化曲線

壓套與開口環之間的相互作用分成3個階段，第1個階段是開口環的徑向變形段，開口環的開口隨著壓套的位移線性減小，2個接觸面之間的接觸應力近似線性增長；由于壓套和開口環之間的幾何尺寸的匹配，當開口環的兩個開口端閉合后，開口環的左端面恰好開始進入壓套的內柱面中，這時進入到第2個階段——過渡段，這一段內伴隨著不同幾何角度接觸面的切換，所以接觸力呈現很大的非線性；第3個階段是開口環完全進入到了壓套的內柱面中，壓套的軸向力僅為較小的摩擦力。

與理論模型研究對象所對應的是徑向變形段，要將模型預測的結果與有限元的計算結果進行比較。在計算公式中，截面慣性矩是未知的，開口環不規則的幾何截面形狀，中性軸的在截面上的位置對截面慣性矩將產生很大的影響，本文采用與有限元計算結果相結合的方法確定截面慣性矩。

圖6所示為3個不同時刻開口環對稱面上的應力分布圖。圖中斜直線所標示的位置為中性軸的大致位置。從圖中可以看出，第1個階段開口環截面的中性軸位置基本上不隨時間發生變化，用CAD軟件求3個時刻截面慣性矩分別為213.2×10-12m4、213.2×10-12m4和215.8×10-12m4，取平均值214.1×10-12m4。據此，理論公式中的所有參量均已確定，將變形過程中若干個過程開口角度帶入即可求得作用在開口端的力。

將開口端的力轉化成軸向力與仿真輸出的結果進行比較，根據幾何關系，轉換的表達式為

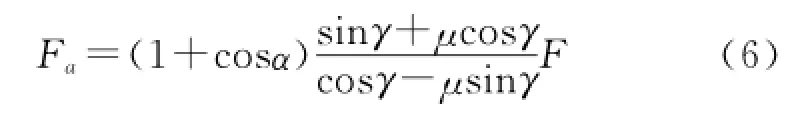
用式（6）計算出開口環不同開口角度時的軸向力，計算結果和有限元計算結果的對比如圖7所示。從初始變形到α＜0．09°，有限元計算結果和理論模型計算結果比較接近，當α＞0．09°，兩者出現了的差異，原因是當開口環變形較大時，其外在幾何形狀不能保持為弧形，除開口端外，開口環的其他部位與壓套的內表面間發生了接觸，假設4）和假設1）同時失效，造成了兩者的誤差，于是理論模型在開口環的變形不是太大時具有較高的精度，而在開口環變形大時，會有一定的誤差。

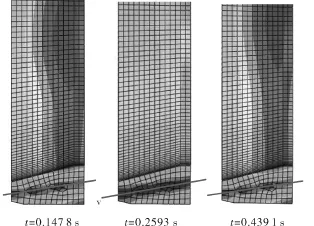
圖6　不同時刻截面的應力分布

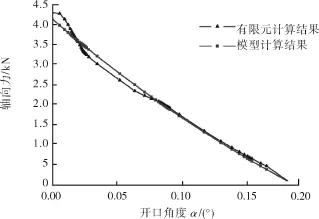
圖7　壓套軸向力的仿真結果和模型計算結果對比

3　結論

1）根據試驗結果和有限元仿真結果，將開口環與壓套的相互作用力等效為作用在開口環開口端上的集中力的簡化方法是合理的。

2）基于所提出的簡化假設，建立了開口環變形過程的數學模型，該模型的計算結果與有限元的計算結果較為吻合。

3）本文提出的數學模型在開口環變形較小時有很高的精度，而在開口環變形較大時，雖然與有限元計算結果之間有微小的差異，但對壓套驅動機構的設計和開口環的結構優化有參考價值。

［1］威特克力公司.卡簧使輕量化成為可能［J］.汽車與配件，2013（18）：38.

［2］王玨.用卡簧來固定軸承［J］.汽車與配件，2013（44）：26-27.

［3］高雪峰，梅明霞，姜靜，等.大井眼卡簧式鉛封防砂封隔器的研制［J］.石油機械，2007（10）：53-54.

［4］楊進，段異生，楊鴻波，等.卡簧式鉆井隔水管快速接頭力學性能研究［J］.石油機械，2010（2）：13-15.

［5］郝忠獻，李根生，高向前，等.滑閥卡簧定位力有限元分析與優化［J］.石油礦場機械，2010，39（1）：50-53.

［6］周俊超，王三武，杜文俊.基于ANSYS的對卡簧包緊力的接觸分析［J］.機械研究與應用，2011（5）：3-5.

［7］溫紀宏，關幼耕，暢元江.隔水管快速接頭卡簧設計與分析［J］.石油機械，2012（12）：43-46.

［8］叢偉，孫明祥.圓截面卡簧的設計探討［J］.機械設計與制造，2003（2）：59-60.

Deformation Analysis of Circlip

YAO Benchun，DING Qingxin，HOU Yue，ZHANG Shimin
（College of Mechanical and Transportation Engineering，China University of Petroleum（Beijing），Beijing 102249，China）

In this paper，the deformation of a circlip adopted in a novel frac sleeve，is analyzed by both theoretical method and FEA method.A Local contact hypothesis is proposed based on exper iment phenomenon and FEA result that the effect of the contact force between the circlip and the compressor could be made equivalent to a concentrated force applied locally on the ends of the cir clip.Together with additional simplification and assumption，a mathematical model based on the energy approach is constructed to express the relationship between the concentrated force and the circlip opening angle.An FEA model is established using ABAQUS code to solve the practical cir clip deformation problem，and the axial reaction force applied on the compressor is acquired to compare with the data computed by the mathematical equation.The fine fitness of the two set of data proves the validity of the local contact hypothesis and the mathematical model.

circlip；cring；sliding sleeve；energy method

TE934.2

A

10.3969／j.issn.1001-3482.2015.12.003

1001-3482（2015）12-0010-05

2015-06-15

中國石油科技創新基金研究項目“水平井大通徑多級壓裂電控滑套技術研究”（2014D-5006-0204）

姚本春（1989-），男，安徽滁州人，博士研究生，主要研究方向為井下工具的設計，Email：yaobenchun＠163.com。