鋁合金關節軸承外圈滾軋整形有限元分析

鄒凱麗, 李寶福, 劉紅宇

(1.上海大學 機電工程與自動化學院,上海 200072；2.上海市軸承技術研究所,上海 201800)

關節軸承是一種球面滑動軸承，其結構由一個帶內球面的外圈和一個帶外球面的內圈組成[1-2]。鋁合金自潤滑關節軸承為外圈內表面粘貼有自潤滑襯墊的關節軸承，其具有結構簡單緊湊、承載大、體積小、重量輕、擺動時工作可靠性高和免維護等優點，廣泛應用于航空航天等機械領域[3-4]。

整體式關節軸承內、外圈的裝配有2種工藝：合套擠壓裝配工藝和擠壓彈性裝配工藝。合套擠壓是將外圈通過塑性成形裝配到內圈上[4]。擠壓彈性裝配工藝則是趁外圈受到徑向擠壓發生彈性變形時，將內圈側身插入外圈，待擠壓力撤消后，旋轉內圈90°，使內外圈軸線重合，完成裝配。

大中型鋁合金關節軸承由于外圈剛度小，彈性變形量大，適合采用擠壓彈性裝配工藝。但由于設計、材料和擠壓力控制等方面的原因，裝配過程中外圈會產生一定塑性變形，如果后續不進行整形，將嚴重影響軸承的承載能力和支承精度。因此，提出鋁合金關節軸承三輥滾軋整形工藝，并通過有限元模擬探討該工藝的可行性。

1 關節軸承裝配后外圈整形方法

1.1 靜壓整形

傳統的外圈整形是一種靜壓方法，利用壓力機在軸承外圈半徑較大的方向上對外圈施加壓力并保壓一段時間，使該方向上的外圈半徑減小，經過測量-靜壓多次操作逐步減小半徑誤差[5-6]。靜壓力的大小和保壓時間主要依靠操作人員的經驗。這種工藝方法對工裝要求不高，但加工效率低，容易把外圈壓出棱角，使軸承旋轉時出現“硬點”(由于外界或自身因素，使軸承幾何形狀、外形尺寸發生突變而引起局部范圍內應力顯著增大的點)等缺陷，廢品率較高。

1.2 三輥滾軋整形

三輥滾軋外圈整形方法如圖1所示，上輥為加載輥，下面2個為支承輥。轉動軸承內圈使其與外圈垂直，并將內圈固定，防止其隨外圈轉動，避免對內圈造成二次損害。F為施加在加載輥上的力，F1，F2分別為從動輥、驅動輥作用在軸承上的力，給驅動輥施加一定的角速度，根據軸承不同位置的半徑誤差改變載荷F的大小對外圈進行整形。驅動輥和從動輥間應保持適當間距，使F1，F2約等于F/2，保證只有加載輥附近的外圈發生塑性變形，驅動輥和從動輥附近的外圈處于彈性變形范圍內。與傳統整形方法相比，三輥滾軋整形法可以對整個外圈連續、多次加載，加工效率高、廢品率低，不會出現“硬點”等缺陷。

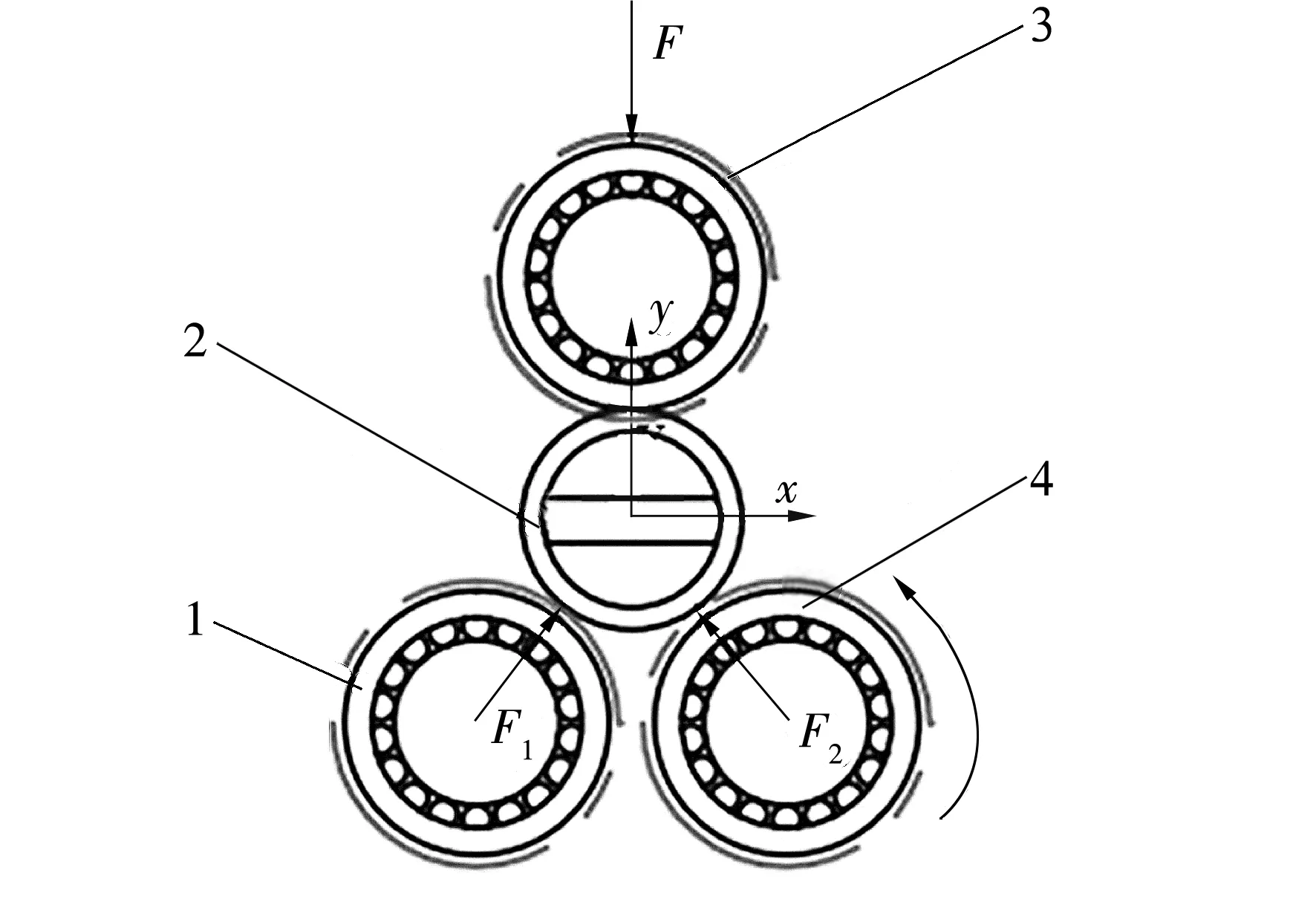
1—從動輥；2—鋁合金關節軸承；3—加載輥；4—驅動輥圖1 三輥滾軋整形示意圖

2 靜壓分析

為考察在三輥夾持下軸承外圈的變形規律，應用ANSYS/LS-DYNA進行靜壓分析，即在輥不轉動的條件下研究外圈的塑性變形規律。

2.1 靜壓分析模型

取GE134鋁合金自潤滑關節軸承外圈為研究對象，其尺寸及材料性能參數見表1。三軋輥直徑均為50 mm。由于內圈與外圈垂直放置，內圈對外圈的影響較小，因此在幾何建模時忽略內圈。另外，整個滾軋工藝系統關于軸承外圈寬度方向二分之一截面對稱，故取其二分之一作為分析模擬的幾何模型[7]，減少模擬計算時間。

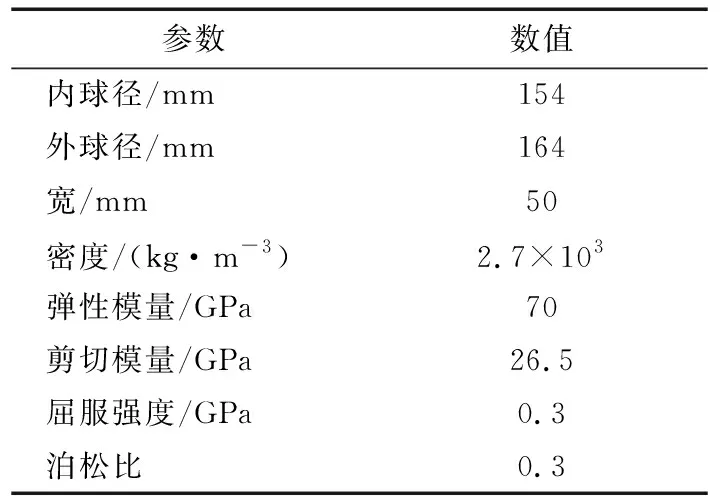
表1 GE134鋁合金關節軸承外圈參數

靜壓分析過程中不考慮輥的變形，即輥的材料模型設為剛體，并且把輥簡化為殼體，將外圈設為雙線性各向同性材料。建立的三維分析模型如圖2所示。根據模型的特點，采用掃略分網與自適應網格劃分相結合的方式將模型劃分為六面體網格。

圖2 靜壓分析三維模型

由于最大位移節點位于外圈與加載輥接觸的中心位置，且僅具有y方向的載荷和位移，與摩擦力無關，因此為簡化分析，將軋輥與鋁合金軸承外圈采用無摩擦的面面接觸模型，軋輥為目標面，外圈表面為接觸面[8-9]。加載輥僅能沿y方向移動，其他自由度均被約束；2個支承輥的自由度為0。對加載輥施加載荷，保持一段時間后卸載，分析不同載荷下軸承的形變。

2.2 仿真分析

2.2.1 應力

在靜止的滾軋力作用下，外圈的典型等效應力分布如圖3所示。由圖可知，Ⅰ，Ⅱ，Ⅲ區應力比較大；除與軋輥接觸的鄰近區域，外圈的應力分布具有明顯的曲梁彎曲特征，即在橫截面上中性軸各點應力為零，應力從內側的壓應力(負)變化為外側的拉應力(正)。由于受到y方向擠壓,Ⅰ，Ⅲ區外表面產生壓應力，內表面產生拉應力；Ⅱ區外表面產生拉應力，內表面產生壓應力。Ⅰ區應力最大，且最大值出現在外圈的對稱面上，隨著距加載輥作用區域距離的增加,應力逐漸減小。加載過程中，非直接受力區域金屬發生橫向堆積，x方向外圈直徑有變大傾向。

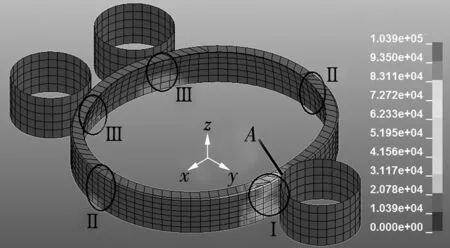
圖3 外圈等效應力圖

2.2.2 應變

外圈變形是復雜的三維變形，包括軸向延伸、徑向壓縮以及橫向展寬。靜壓分析過程中軸承外圈等效應變及節點軸向位移如圖4、圖5所示。由圖可知，Ⅰ，Ⅱ，Ⅲ區應變比較大，且靠近加載輥的外圈外表面，由于受到擠壓在z方向產生延伸出現拉伸應變，其最大值出現在與加載輥的接觸點，以接觸點為中心，離接觸點越遠外圈應變越小，并逐步下降至0。由于延伸應變主要伸向外圈端面，造成端面部位金屬堆積，同時使外圈內表面出現壓縮應變。

圖4 外圈應變圖

圖5 節點軸向位移圖

外圈節點徑向位移如圖6所示。由圖可知，外圈橫向非加載區域金屬堆積，外圈出現徑向壓縮、橫向展寬，即外圈y方向半徑減小，x方向半徑增大，且變形關于y軸對稱。加載輥附近的外圈變形量大于驅動輥和從動輥附近的變形量。

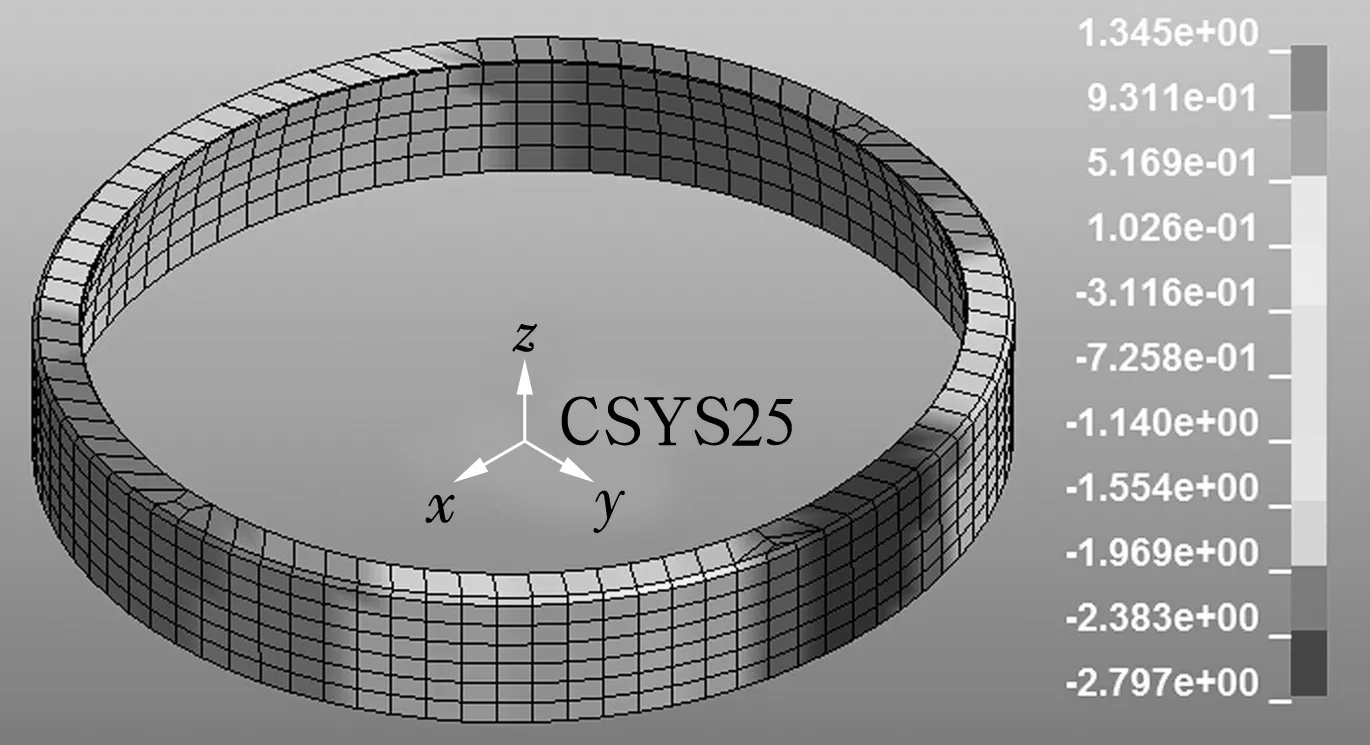
圖6 節點徑向位移

2.2.3 載荷-位移曲線

由靜壓分析可知:當載荷大于100 kN時外圈被壓潰；當載荷小于4 kN時外圈幾乎沒有塑性變形；此外當載荷大于12 kN時，卸載后節點最大徑向位移大于3 mm。根據載荷-位移關系結合外圈半徑誤差，滾軋整形時載荷應控制在(4～12) kN。此范圍內撤銷載荷后軸承外圈節點的最大徑向位移與載荷的關系如圖7所示。

圖7 載荷-位移曲線

以載荷為6 kN為例，以加載輥與外圈接觸點A為中心，圓周方向二分之一橫截面節點坐標曲線如圖8所示。由圖可知，加載輥附近外圈被擠壓變形，外圈橫向半徑伸長。

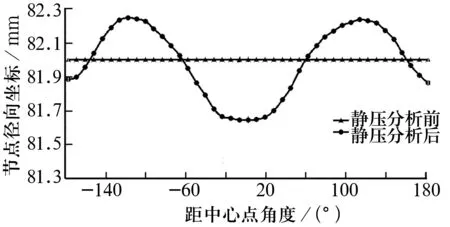
圖8 二分之一橫截面節點坐標曲線

3 滾軋整形模擬

為進一步研究實際轉動情況下，外圈的變形與滾軋力之間的關系，運用ANSYS/LS-DYNA進行外圈滾軋整形模擬[10-11]。

3.1 滾軋力及整形分析模型

擠壓彈性裝配后的外圈外圓輪廓一般近似于橢圓。假設整形前外圈的外圓輪廓為橢圓，則外圈外圓輪廓半徑誤差為

(1)

式中：a為長軸半徑；b為短軸半徑；θ為r軸(外圓輪廓上的變形點所在半徑方向)與y軸夾角。

理想的滾軋整形力F與外圈材料、結構、外圓輪廓誤差有關，是一個復雜的函數。這里參考控制論中最簡單的一種反饋控制策略——比例反饋算式，再考慮到壓力的非負性，取滾軋整形力F為

F(θ)=Kε(θ)+c，

(2)

式中：K為比例系數；c為常數。

滾軋整形時加載輥具有y方向的移動自由度以及繞自身軸線的轉動自由度，驅動輥和從動輥只具有繞自身軸線轉動的自由度。其他參數與靜壓分析模型相同。

3.2 仿真結果分析

仍以GE134鋁合金自潤滑關節軸承為例，設整形前外圈大、小端直徑分別為165，163 mm，圓度為1 mm。取K1=2.2×104N/mm，c1=2.5 kN進行第1次滾軋；K2=0.8×104N/mm，c2=0.6 kN進行第2次滾軋。

滾軋整形前、后外圈圓周方向各采集點徑向坐標如圖9所示。由圖可知，滾軋整形前外圈圓度為1 mm，第1次滾軋后外圈圓度為0.206 5 mm，第2次滾軋后外圈圓度為0.069 0 mm。通過滾軋整形模擬可以看出，滾軋整形后外圈圓度明顯提高，且第2次滾軋后外圈圓度明顯小于第1次滾軋后。由此可以得出，通過多次滾軋整形外圈圓度將趨于零，可以滿足使用要求。

圖9 滾軋前后節點徑向坐標

4 結束語

鋁合金自潤滑關節軸承整形過程中既有徑向壓縮和軸向延伸，又存在橫向擴展；材料具有非線性，而且其邊界條件復雜，只有充分考慮上述多種因素，才能得到成形過程比較真實的描述。整形過程中，加載輥附近外圈受壓應力作用，隨著離加載輥作用區域距離的增加，壓應力最終變為拉應力，外圈產生徑向壓縮和橫向擴展。

通過比例反饋加載進行滾軋整形模擬，雖然在一定程度上可以提高軸承的圓度，但整形過程還有很大的不穩定性，需對反饋機制繼續進行探討。