基于擴(kuò)張狀態(tài)觀測器的永磁同步電機(jī)滑模變結(jié)構(gòu)位置伺服控制

陳強(qiáng)，陶亮，南余榮，董方（浙江工業(yè)大學(xué) 信息工程學(xué)院，浙江杭州 310023）

基于擴(kuò)張狀態(tài)觀測器的永磁同步電機(jī)滑模變結(jié)構(gòu)位置伺服控制

陳強(qiáng)，陶亮，南余榮，董方
（浙江工業(yè)大學(xué) 信息工程學(xué)院，浙江杭州 310023）

摘要：針對帶有未知摩擦力矩和模型不確定的永磁同步電機(jī)位置伺服系統(tǒng)，提出兩種基于擴(kuò)張狀態(tài)觀測器的滑模變結(jié)構(gòu)位置伺服控制策略。在系統(tǒng)存在狀態(tài)未知和非線性特性有界的情況下，設(shè)計(jì)擴(kuò)張狀態(tài)觀測器來觀測系統(tǒng)的未知狀態(tài)和非線性不確定項(xiàng)，并根據(jù)觀測值設(shè)計(jì)降階線性滑模控制和無抖振全階滑模控制兩種控制方法。仿真結(jié)果表明，降階滑模控制方法控制精度較高且魯棒性較強(qiáng)，而全階滑模控制方法可以有效消除滑模控制中的抖振問題，便于實(shí)際應(yīng)用。

關(guān)鍵詞：永磁同步電動機(jī)；位置伺服系統(tǒng)；滑模變結(jié)構(gòu)控制；擴(kuò)張狀態(tài)觀測器

本文引用格式：陳強(qiáng)，陶亮，南余榮，等.基于擴(kuò)張狀態(tài)觀測器的永磁同步電機(jī)滑模變結(jié)構(gòu)位置伺服控制[J].新型工業(yè)化，2015，5（8）：17-25

Citation: CHEN Qiang, TAO Liang, NAN Yu-rong, et al. Sliding-mode Variable Structure Position Servo Control of Permanent Magnet Synchronous Motor Based on Extended State Observer[J]. The Journal of New Industrialization, 2015, 5（8）: 17-25.

0 引言

永磁同步電機(jī)（permanent magnet synchronous motor，PMSM）具有體積小、結(jié)構(gòu)簡單、氣隙磁密高、轉(zhuǎn)矩慣量大等優(yōu)點(diǎn)，因此在諸如機(jī)器人，航天飛行器以及升降機(jī)等高性能系統(tǒng)的應(yīng)用中已經(jīng)取代直流電機(jī)，成為近些年來的研究熱點(diǎn)[1-3]。由于永磁同步電機(jī)位置伺服控制系統(tǒng)本身具有非線性、時變性和強(qiáng)耦合性，且伺服對象往往也存在著較強(qiáng)的不確定性和擾動，因此，對于有高性能、高精度要求的伺服系統(tǒng)來說，傳統(tǒng)的線性PID控制已不能滿足其需求，尤其是當(dāng)控制系統(tǒng)受到模型不確定和未知摩擦等非線性干擾時，控制器將很難兼顧動態(tài)響應(yīng)和抗干擾能力的要求，從而導(dǎo)致控制性能進(jìn)一步降低。

為提高系統(tǒng)的控制性能和魯棒性，許多先進(jìn)的非線性控制技術(shù)被應(yīng)用于永磁同步電機(jī)伺服控制系統(tǒng)，如自抗擾控制[4]、自適應(yīng)控制[5]、魯棒控制[6]、滑模控制[7]和有限時間控制[8]等。其中，滑模控制（sliding-mode control，SMC）由于其對擾動和不確定性具有良好的魯棒性，因而被廣泛應(yīng)用于各種伺服控制系統(tǒng)中。但是滑模控制中不連續(xù)項(xiàng)的存在，導(dǎo)致系統(tǒng)控制律中存在一定的抖振問題，嚴(yán)重影響了電機(jī)系統(tǒng)的精確定位和位置跟蹤性能，甚至?xí)﹄姍C(jī)系統(tǒng)本身造成損害[9]。因此，在高性能永磁同步電機(jī)位置伺服系統(tǒng)中，如何削弱滑模控制中的抖振現(xiàn)象，是一個亟待解決的關(guān)鍵技術(shù)難題。

近些年，為了削弱傳統(tǒng)滑模控制中的抖振問題，國內(nèi)外已提出很多改進(jìn)的滑模控制方法。文獻(xiàn)[10]在控制器的設(shè)計(jì)過程中，采用了飽和函數(shù)來替代一般滑模控制中的切換項(xiàng)。該設(shè)計(jì)方法在削弱滑模抖振現(xiàn)象的同時，也減弱了傳統(tǒng)滑模的魯棒性能。文獻(xiàn)[11]提出一種積分時變滑模控制器，在滑模面設(shè)計(jì)中引入誤差的積分項(xiàng)和時變項(xiàng)，有效減小了滑模抖振并提高了誤差收斂速度；文獻(xiàn)[12]將滑模控制與自適應(yīng)機(jī)制相結(jié)合，設(shè)計(jì)自適應(yīng)滑模控制器，實(shí)時地更新切換增益，取得了較好的控制效果。然而，以上控制方法雖然在削弱滑模抖振方面均取得了一定效果，但卻要求所有的系統(tǒng)狀態(tài)是完全可測的，且未考慮摩擦力矩和模型不確定項(xiàng)引起的未知擾動對永磁同步電機(jī)控制性能的影響。

文獻(xiàn)[13]和[14]分別將擾動觀測器和擴(kuò)張狀態(tài)觀測器與滑模控制相結(jié)合，用于永磁同步電機(jī)的調(diào)速控制。由于觀測器對未知擾動具有一定的補(bǔ)償作用，控制器增益被降低，從而在一定程度上減小了滑模抖振，但由于控制信號的不連續(xù)性，仍不能消除滑模控制器的抖振問題。近來，文獻(xiàn)[15]提出了一種無抖振滑模控制方法，該控制器是一種全階滑模控制器，與傳統(tǒng)的降階滑模控制器相比，控制信號是連續(xù)的，能夠有效避免滑模抖振問題。

本文針對帶有未知摩擦力矩和模型不確定項(xiàng)的永磁同步電機(jī)位置伺服系統(tǒng)，提出兩種基于擴(kuò)張狀態(tài)觀測器的永磁同步電機(jī)滑模變結(jié)構(gòu)位置伺服控制方法。設(shè)計(jì)擴(kuò)張狀態(tài)觀測器來觀測系統(tǒng)狀態(tài)及摩擦力矩和模型不確定項(xiàng)等非線性特性，并使用觀測值來設(shè)計(jì)降階線性滑模控制器和無抖振全階滑模控制器，實(shí)現(xiàn)電機(jī)輸出位置對期望軌跡的快速精確跟蹤。

1 永磁同步電機(jī)數(shù)學(xué)模型

在d/q旋轉(zhuǎn)坐標(biāo)系下，永磁同步電機(jī)的數(shù)學(xué)模型可表示為：

其中，ud、uq分別為d、q軸上的電壓分量；id、iq為d、q軸上的電流分量；J為系統(tǒng)的轉(zhuǎn)動慣量；R為定子電阻；pn為極對數(shù)；Ld、Lq分別為d、q軸上的電感分量； Ψf為永磁體基波勵磁磁鏈；ω為轉(zhuǎn)子的角速度；Te為電磁轉(zhuǎn)矩；TL為負(fù)載轉(zhuǎn)矩； B為摩擦系數(shù)。

為了實(shí)現(xiàn)伺服系統(tǒng)的高性能控制，在實(shí)際應(yīng)用中，常采用id=0的轉(zhuǎn)子磁場定向控制方法，其永磁同步電機(jī)位置伺服系統(tǒng)框圖如圖1所示。

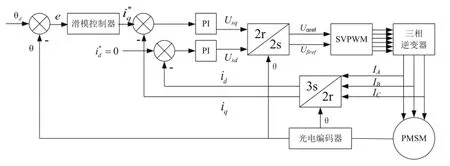
圖1 永磁同步電機(jī)位置伺服控制系統(tǒng)框圖Fig.1 Schematic diagram of PMSM position control system

由式（1）-（3），可得永磁同步電機(jī)位置環(huán)的二階動態(tài)方程為

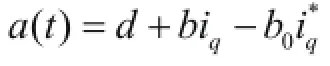
本文的控制目的為通過設(shè)計(jì)控制信號 ()ut，使得永磁同步電機(jī)的實(shí)際輸出位置y能夠精確跟蹤期望軌跡yd。

2 擴(kuò)張狀態(tài)觀測器設(shè)計(jì)

其中，β1,β2,β3＞0為觀測器增益.fal(·)為原點(diǎn)附近具有線性段的連續(xù)冪次函數(shù)，表達(dá)式為：

由文獻(xiàn)[16]，[17]可知，當(dāng)選擇適當(dāng)?shù)膮?shù)βi，函數(shù)fal(·)可以使得觀測器狀態(tài) zi→xi，即：觀測|x－z|≤l l＞0誤差可以收斂到，其中為很小的正數(shù)。

3 滑模變結(jié)構(gòu)控制

定義跟蹤誤差為

則e的一階和二階導(dǎo)數(shù)分別為

和

3.1 降階滑模控制器設(shè)計(jì)

由式（9）和式（10），降階線性滑模面可設(shè)計(jì)為

對式（12）求導(dǎo)，由式（9）-（11）可得

由式（13），基于擴(kuò)張狀態(tài)觀測器（7）的降階滑模控制器可設(shè)計(jì)為

3.2 全階滑模控制器設(shè)計(jì)

根據(jù)式（9）-（11），設(shè)計(jì)如下全階滑模面

其中，10λ＞和20λ＞為控制參數(shù)。

將式（9）-（11）代入式（15），可得

由式（16），基于擴(kuò)張狀態(tài)觀測器（7）的全階滑模控制器可設(shè)計(jì)為

由式（17）-（20）可以看出，通過加入一階濾波器1/(s+T)以后，只有u2中含有滑模切換項(xiàng)sgn(s)，而實(shí)際控制信號u中并不包含該切換項(xiàng)。因此，該控制器能夠消除由于滑模切換項(xiàng)而造成的抖振問題。

將式（17）-（20）代入式（16）中，有

設(shè)計(jì)與研究

其中，d(x,z)=(x3－z3)+λ2(x2－z2)+λ1(x1－z1)，且滿足d(x,z)≤ld，ld=l3+λ2l2+λ1l1。

對式（21）求導(dǎo)可得

3.3 穩(wěn)定性證明

以下引理和定理給出了系統(tǒng)（5）的穩(wěn)定性證明。

引理1[2]：假設(shè)存在一個連續(xù)、正定的函數(shù)()Vt，滿足以下微分方程：

其中，0α＞和01η＜＜是常數(shù)。則對于任意給定的t0，存在一個有限時間t1，使得以下不等式和等式成立：

和

定理1：給定不確定永磁同步電機(jī)位置伺服系統(tǒng)（5）和降階滑模面（12），設(shè)計(jì)擴(kuò)張狀態(tài)觀測器（7）和控制器（14），則當(dāng)控制參數(shù)k1滿足k1≥|ε3|+λ0|ε2|時，跟蹤誤差e將穩(wěn)定收斂至零點(diǎn)。

證明：針對系統(tǒng)（6），構(gòu)建如下Lyapunov函數(shù)

對V求導(dǎo)，由式（12）-（14）可得

因此，當(dāng)k1滿足k1≥|ε3|+λ0|ε2|時，有

11時，V(t)=0恒成立，即滑模面s1可在有限時間內(nèi)快速穩(wěn)定地收斂至零點(diǎn)。

由式（12）可得，在滑模面s1=0上有e.+λ0e=0恒成立，因此，當(dāng)t→∞時，跟蹤誤差e將穩(wěn)定收斂至零點(diǎn)。

定理2：針對永磁同步電機(jī)伺服控制系統(tǒng)（5），設(shè)計(jì)全階滑模面（15）及控制器（17）-（20），當(dāng)控制參數(shù)kd和kT分別滿足kd≥|d.(x,z)|，kT≥Tld時，跟蹤誤差e將穩(wěn)定收斂至零點(diǎn)。

證明：針對系統(tǒng)（5），構(gòu)建如下Lyapunov函數(shù)

對V求導(dǎo)，由式（17）-（20）可得

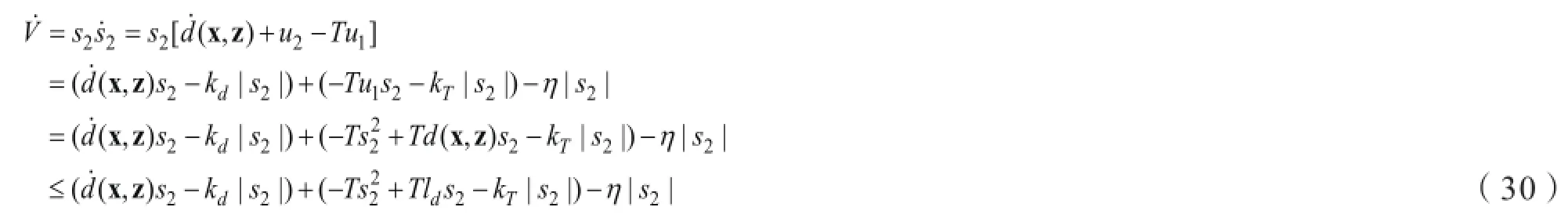
當(dāng)kd和kT分別滿足時，可得

由式（15）可得，在滑模面s2=0上有：

式（32）可以進(jìn)一步改寫為：

其中，0＜λ0＜λ2且滿足(λ2－λ0)λ0=λ1。

定義

則式（33）可以改寫為

因此，當(dāng)t→∞時，可得0χ→成立，由式（34）可以推導(dǎo)得出跟蹤誤差e將穩(wěn)定收斂至零點(diǎn)。

4 仿真研究及結(jié)果

設(shè)計(jì)與研究

為了分析和對比基于擴(kuò)張狀態(tài)觀測器的降階滑模控制（reduced-order sliding mode control based on extended state observer，RSMC+ESO）與基于擴(kuò)張狀態(tài)觀測器的全階滑模控制（full-order sliding mode control based on extended state observer，F(xiàn)SMC+ESO）兩種控制方法的優(yōu)劣性，本節(jié)對永磁同步電機(jī)位置伺服控制系統(tǒng)進(jìn)行了仿真研究。仿真中PMSM系統(tǒng)、控制器和擴(kuò)張狀態(tài)觀測器參數(shù)分別給定如下。

PMSM參數(shù)設(shè)置為：額定功率P=0.2kW，額定轉(zhuǎn)速ω=3000r/min，永磁體磁鏈Ψf=0.371Wb ，極對數(shù)Pn=4，d-q軸電感Ld=Lq=30mH，轉(zhuǎn)動慣量J=0.17kg·cm2，粘性阻尼系數(shù)B=0.001N·m/(r/min)；擴(kuò)張狀態(tài)觀測器參數(shù)設(shè)置為：β1=β2=β3=100，δ=0.01，b0=10；控制器參數(shù)分別設(shè)置為：k1=k2=20，λ0=λ2=2，λ1=5，T=0.01。為便于兩種控制方法的比較，本節(jié)分別針對正弦信號和階躍信號的跟蹤效果進(jìn)行對比，對比效果如圖2和圖3所示。

圖2給出了當(dāng)負(fù)載TL=2Nm，跟蹤位置為正弦信號時，采用RSMC+ESO與FSMC+ESO兩種控制方法的正弦曲線跟蹤效果對比。其中，圖2（a）和圖2（b）為分別采用兩種控制方法時的位置跟蹤曲線和跟蹤誤差曲線對比，圖2（c）為兩種控制方法的控制信號對比。圖2（d）為兩種方法中擴(kuò)張狀態(tài)觀測器的觀測誤差對比。從圖2（a）可以看出，采用FSMC+ESO方法比RSMC+ESO方法有更快的跟蹤速度，但從圖2（b）和圖2（c）可以看出，F(xiàn)SMC+ESO方法的正弦曲線跟蹤的穩(wěn)態(tài)誤差雖然略大于RSMC+ESO方法，但控制信號的抖振卻明顯小于RSMC+ESO方法。

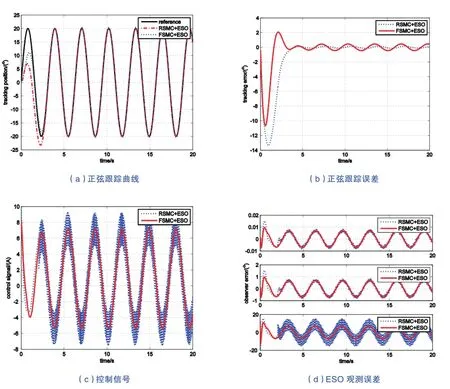
圖2 兩種控制方法的正弦波跟蹤對比Fig.2 Sine wave tracking comparison of two control methods

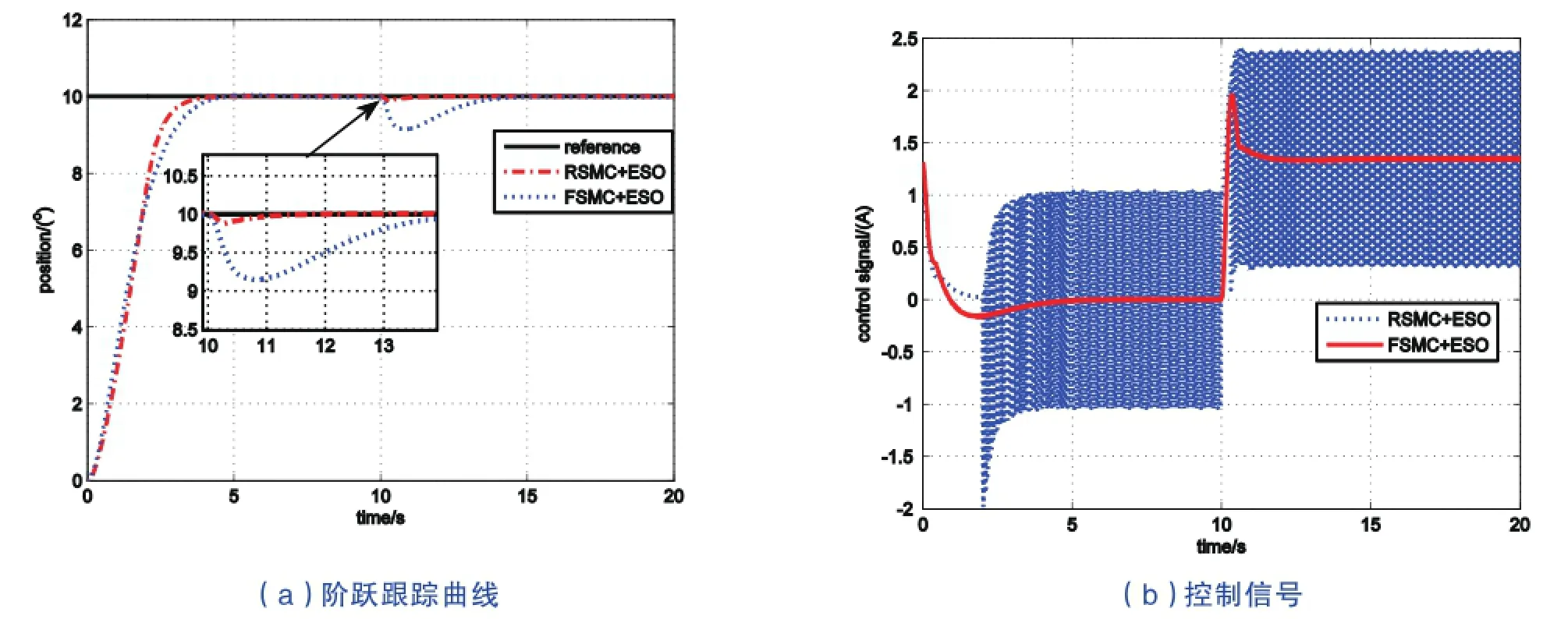
圖3 兩種控制方法的階躍跟蹤對比Fig.3 Step tracking comparison of two control methods

為進(jìn)一步比較兩種控制方法的優(yōu)缺點(diǎn)，圖3給出了初始負(fù)載為空載，位置給定為階躍信號時的跟蹤效果和控制信號。其中，圖3（a）給出了采用RSMC+ESO與FSMC+ESO兩種控制方法的階躍信號跟蹤效果，并且在t=10s時突加了負(fù)載擾動TL=3Nm，圖3（b）為兩種控制方法的控制信號。從圖3（a）可以看出，在t=10s時突加負(fù)載TL=3Nm以后，RSMC+ESO方法能夠更快地做出反應(yīng)并及時跟蹤上位置給定，而FSMC+ESO方法則較慢，系統(tǒng)產(chǎn)生相對較大的位置跟蹤滯后。因此，RSMC+ESO方法比FSMC+ESO方法有更好的魯棒性。然而，圖3（b）給出的控制增益曲線表明，RSMC+ESO方法的控制信號抖振較大，而FSMC+ESO方法的控制信號幾乎無抖振問題。

5 結(jié)論

本文考慮摩擦力矩和模型不確定項(xiàng)引起的未知擾動對永磁同步電機(jī)控制性能的影響，設(shè)計(jì)兩種基于擴(kuò)張狀態(tài)觀測器的永磁同步電機(jī)滑模變結(jié)構(gòu)位置伺服控制方法。 采用擴(kuò)張狀態(tài)觀測器來觀測系統(tǒng)狀態(tài)及摩擦力矩和模型不確定項(xiàng)等非線性特性，并使用觀測值來設(shè)計(jì)控制和全階滑模控制方法，保證電機(jī)輸出位置精確跟蹤期望軌跡。仿真結(jié)果表明，RSMC+ESO方法具有更好的穩(wěn)態(tài)跟蹤精度和魯棒性，而FSMC+ ESO方法基本無抖振問題，便于實(shí)際應(yīng)用。

參考文獻(xiàn)

[1] 唐任遠(yuǎn). 現(xiàn)代永磁電機(jī)理論與設(shè)計(jì)[M]. 北京： 機(jī)械工業(yè)出版社，2000. R Y Tang. Modern permanent magnet machines theory and design[M]. Beijing： Machinery Industry Press，2000.

[2] Chen Q，Yu L，Nan Y R. Finite-time tracking control for motor servo systems with unknown dead-zones[J]. Journal of Systems Science and Complexity，2013，26（6）： 940-956.

[3] Na J，Chen Q，Ren X M，et al. Adaptive prescribed performance motion control of servo mechanisms with friction compensation[J]. IEEE Transactions on Industrial Electronics，2014，61（1）： 486-494.

[4] 邵立偉，廖曉鐘，張宇河，等. 自抗擾控制器在永磁同步電機(jī)控制中的應(yīng)用[J]. 北京理工大學(xué)學(xué)報，2006，26（4）： 326-329. L W Shao，X Z Liao，Y H Zhang，et al. Active disturbance rejection controller scheme for permanent magnetic synchronous motor [J]. Transactions of Beijing Institute of Techonlogy，2006，26（4）： 326-329.

[5] 陳強(qiáng)，吳根忠，葉雷. 永磁同步電機(jī)變負(fù)載自適應(yīng)神經(jīng)網(wǎng)絡(luò)控制[J]. 新型工業(yè)化，2014，4（4）：17-22. Q Chen，G Z Wu，L Ye. Adaptive neural control of permanent magnet synchronous motor with variable load[J]. The Journal of New Industrialization，2014，4（4）： 17-22.

[6] 林立，黃蘇融. 永磁同步電機(jī)系統(tǒng)線性化H_∞魯棒控制[J]. 電機(jī)與控制學(xué)報，2009，13（4）： 541-552. L Lin，S R Hang. Robust control with linearization technique for interior permanent magnet synchronous motor servo system[J]. Machines and Control，2009，13（4）： 541-552.

[7] 許敘遙，林輝. 基于動態(tài)滑模控制的永磁同步電機(jī)位置速度一體化設(shè)計(jì)[J]. 電工技術(shù)學(xué)報，2014，29（5）： 77-82. X Y Xu，H Lin. Integrated design for permanent magnet synchronous motor servo systems based on dynamic sliding mode control[J]. Transactions of China Electrotechnical Society，2014，29（5）： 77-82.

[8] 劉慧賢，丁世宏，李世華，等. 永磁同步電機(jī)位置伺服系統(tǒng)的有限時間控制[J]. 電機(jī)與控制學(xué)報，2009，13（3）： 424-430. H X Liu，S H Ding，S H Li，et al. Finite-time control of PMSM position servo system[J]. Electric Machnies and Control，2009，13（3）：424-430.

[9] 黃佳佳，周波，李丹，等. 滑模控制永磁同步電動機(jī)位置伺服系統(tǒng)抖振[J]. 電工技術(shù)學(xué)報，2009，24（11）： 41-47. J J Hang，B Zhou，D Li，et al. Sliding mode control for permanent magnet synchronous motor servo system[J]. Transactions of China Electrotechnical Society，2009，24（11）： 41-47.

[10] Utkin V. Sliding modes in control and optimization [M]. Berlin，Germany： Springer-Verlag，1992.

[11] 陳振，耿潔，劉向東. 基于積分時變滑模控制的永磁同步電機(jī)調(diào)速系統(tǒng)[J]. 電工技術(shù)學(xué)報，2011，26（6）： 56-61. Z Chen，J Geng，X D Liu. An integral and exponential time-varying sliding mode control of permanent magnet synchronous motors[J]. Transac-tions of China Electrotechnical Society，2011，26（6）： 56-61.

[12] 付培華，陳振，叢炳龍，等. 基于反步自適應(yīng)滑模控制的永磁同步電機(jī)位置伺服控制系統(tǒng)[J]. 電工技術(shù)學(xué)報，2013，28（9）： 288-293. P H Fu，Z Chen，B L Cong，et al. A position servo system of permanent magnet synchronous motor based on back-stepping adaptive sliding mode control[J]. Transactions of China Electrotechnical Society，2013，28（9）： 288-301.

[13] 張小華，劉慧賢，丁世宏，等. 基于擾動觀測器和有限時間控制的永磁同步電機(jī)調(diào)速系統(tǒng)[J]. 控制與決策，2009，24（7）： 1028-1032. X H Zhang，H X Liu，S H Ding，et al. PMSM speed-adjusting system based on disturbance observer and finite-time control[J]. Control and Decision，2009，24（7）： 1028-1032.

[14] Li S H，Zhou M M，Yu X H. Design and Implementation of terminal sliding mode control method for PMSM speed regulation system[J]. IEEE Transactions on Industrial Informatics，2013，9（4）： 1879-1891.

[15] Feng Y，Han F L，Yu X H. Chattering-free full-order sliding-mode control[J]. Automatica，2014，50（4）： 1310-1314.

[16] 韓京清. 自抗擾控制技術(shù)：估計(jì)補(bǔ)償不確定因素的控制技術(shù)[M]. 北京： 國防工業(yè)出版社，2008. J Q Han. Active disturbance rejection control technique： the technique for estimating and compensating the uncertainties[M]. Beijing：National Defense Industry Press，2008.

[17] 代志綱，岳巍澎，隋曉雨，等. 自抗擾控制技術(shù)的原理剖析[J]. 新型工業(yè)化，2015，5（1）：49-58. Z G Dai，W P Yue，X Y Sui，et al. Dissection on the principle of active disturbance rejection control technology[J]. The Journal of New Industrialization，2015，5（1）： 49-58.

DOI：10.3969/j.issn.2095-6649.2015.08.004

*基金項(xiàng)目：國家自然基金資助項(xiàng)目（61403343）

作者簡介：陳強(qiáng)（1984-），男，講師，博士，主要研究方向：非線性伺服系統(tǒng)建模與控制；陶亮（1990-），男，學(xué)生，碩士，主要研究方向：參數(shù)辨識與伺服系統(tǒng)摩擦建模補(bǔ)償；南余榮(1966-)，男，教授，博士，主要研究方向：電力傳動及其自動化，運(yùn)動控制;董方（1991-），男，學(xué)生，碩士，主要研究方向：多電機(jī)同步驅(qū)動系統(tǒng)

Sliding-mode Variable Structure Position Servo Control of Permanent Magnet Synchronous Motor Based on Extended State Observer

CHEN Qiang, TAO Liang, NAN Yu-rong, DONG Fang
(College of Information Engineering, Zhejiang University of Technology, Hangzhou, 310023)

ABSTRACT:In this paper, two sliding-mode variable structure control (SMVSC) methods are proposed for permanent magnet synchronous motor (PMSM) servo control system with unknown friction torque and model uncertainty based on extended state observer (ESO). In the case of unknown system states and the bounded nonlinear characteristics, the ESO is designed to observe the unknown system states and nonlinear uncertainties, and then a reduced-order sliding mode control (RSMC) and a full-order sliding mode control (FSMC) schemes are both presented based on the ESO observations. Simulation results show that the RSMC performs better than FSMC with respect to tracking accuracy and robustness to load, while FSMC can effectively eliminate the chattering problem, which is more convenient for practical applications.

KEYWORDS:Permanent magnet synchronous motor; Position servo system; Sliding-mode variable structure control; Extended state observer