基于有限元的超精密平面磨床砂輪與主軸過盈配合特性研究

蘇曉東，錢 煒

（上海理工大學 機械工程學院，上海 200093）

0 引 言

為了滿足機床高動態、高熱態性能的要求，機床轉動部件之間的裝配越來越多采用過盈配合。這種連接方式具有很多優點，但同時也具有一些缺陷。過大的過盈量會造成轉動部件之間裝配困難，也加大裝配表面應力。在高速旋轉階段產生的離心力會使得轉動部件之間發生徑向脫離現象。白釗等［1］根據GD－Ⅱ型主軸與電機轉子過盈配合的連接特點通過有限元法對轉子和主軸的配合面進行了詳細的應力應變分析。王建［2］通過對HSK主軸與刀柄的過盈配合進行非線性接觸分析，深入地研究了過盈配合量及轉速等因素對主軸／刀柄接口的變形、應力分布、剛度和承載能力的影響規律。

本文以某公司生產的超精密平面磨床為研究對象，根據彈性力學和動力學理論并通過有限元法對砂輪與主軸的過盈配合進行了詳細的非線性接觸分析，得到了過盈量、轉速及摩擦系數對過盈面連接特性的影響規律，從而為磨床砂輪的裝配工藝提供理論指導。

1 結構介紹

本文研究的電主軸適用于超精密磨削的大功率電主軸，其額定功率為15 kW，最高轉速為8 000 r／min，額定轉矩為65 N m。為了滿足磨削時的高動態，高熱態特性，和砂輪磨削的穩定性與精度，砂輪轂與主軸通過一段長度為70 mm的接觸面過盈連接裝配在一起，其裝配剖面圖如圖1所示。主軸使用合金鋼材料，砂輪輪轂使用55號結構鋼，它們的材料屬性如表1所示。

2 裝配體有限元模型的建立

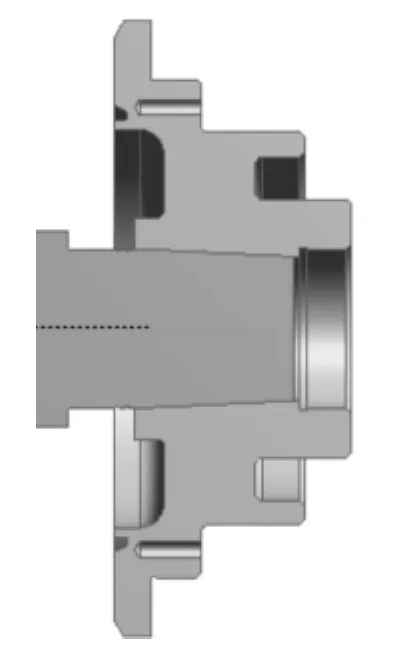
圖1 砂輪轂—軸過盈配合剖面圖

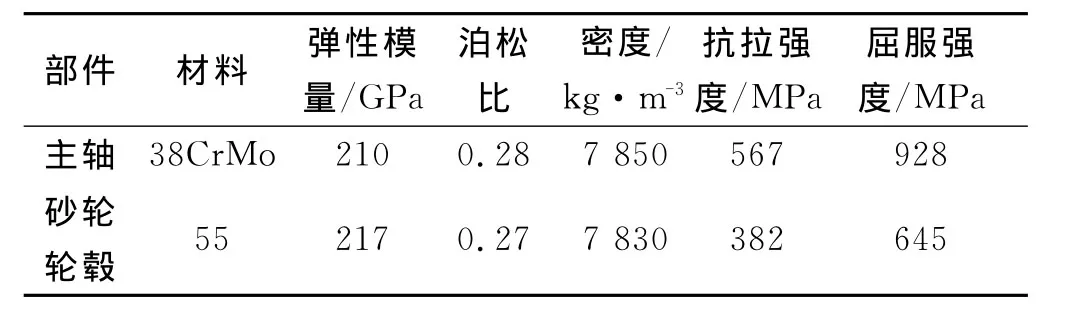
表1 材料屬性

過盈配合產生的接觸應力過大或者過小都直接影響砂輪與磨床主軸的壽命和性能好壞。過盈配合屬于接觸非線性的范疇，靜態接觸問題作為高度非線性的復雜問題。其具有接觸面積和壓力分布隨外載荷的變化而變化的特點，它不能在開始計算時就給出邊界條件，同時兩接觸面間還存著接觸傳熱［3］。接觸問題又將導致計算結果很難收斂。當模型很復雜并且考慮摩擦的動態接觸時，節點將會導致模型的結構離散和方程求解變的困難，從而增加問題的復雜性［4～7］，在面面接觸模型中是把兩個接觸面劃分成目標面與接觸面，當一凸表面或一凹面及平面接觸時，一般選取凸面作為接觸面，凹面作為目標面［8］。因此本文在建立有限元模型時做以下幾個步驟：（1）考慮到裝配體的對稱性和計算機的容量與計算速度，根據有限元理論采用四分之一模型進行接觸分析。（2）將兩個接觸面簡化成一樣的網格，并把相應的節點對應起來，接觸力通過節點傳遞［9］；在有限元軟件ANSYS Workbench中采用多區域劃法對裝配體模型進行網格劃分，對接觸面處的網格進行細化，共得到44 343個節點，9 442個單元，有限元模型如圖2所示。（3）在ANSYS Workbench中將砂輪輪轂設為目標面，主軸外表面設為接觸面。（4）由于軸承對軸的支承方式對砂輪轂—軸過盈配合幾乎沒有影響，故在砂輪輪轂及主軸左右兩端施加軸向約束和徑向約束，在對稱面施加對稱約束。

3 計算結果分析與討論

3.1 過盈量對過盈配合面特性的影響

主軸在最高工作轉速8 000 r／min、過盈量為0.015的裝配體應力云圖如圖3所示，最大等效應力為354 MPa，發生在配合面的右端面。在最高轉速下，過盈配合面的最大合應力及最大接觸壓力隨過盈量變化的曲線如圖4所示。

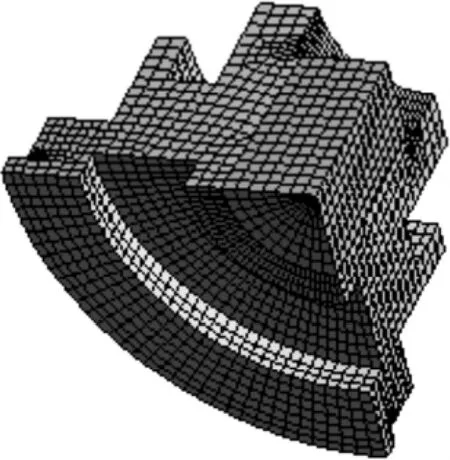
圖2 砂輪輪轂與軸的有限元模型

圖3 轉速為8 000 r／min過盈量為0.015 mm時的等效應力云圖

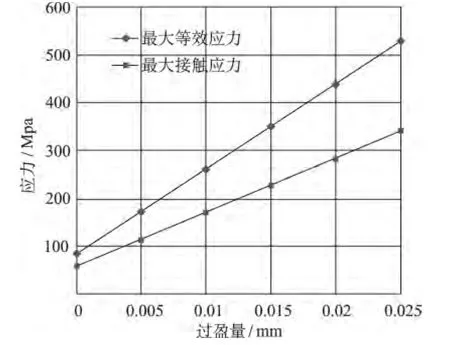
圖4 應力隨過盈量變化曲線圖

由圖4可以看出當過盈量增大時，最大等效應力也逐漸增大，當過盈量達到0.02 mm時，最大等效應力已經達到442 MPa，此時已經超過了砂輪輪轂材料的強度極限382 MPa，由圖4可推斷當過盈量繼續增大時，最大等效應力將繼續逐漸增大，將超過砂輪輪轂的強度極限。同樣最大接觸壓力也是隨著過盈量增大而逐步增大的，在相同過盈量的情況下，最大等效應力是大于最大接觸壓力的。在砂輪輪轂與主軸過盈量為0的情況下計算接觸壓應力時，給砂輪輪轂和主軸施加一個8 000r／min的轉速，高速旋轉時將產生離心力，從而離心力將導致砂輪輪轂與主軸產生部分接觸，繼而導致產生接觸壓應力。但是在實際情況下這種過盈量為0的裝配方式，是不能保證砂輪正常運轉的。計算這種情況下的接觸應力只是為了找出一個臨界過盈量，在該臨界情況下，磨床主軸的扭矩通過砂輪輪轂與磨床主軸的接觸部分傳遞給砂輪，從而使砂輪可以正常工作。

接觸壓力是影響過盈配合面發生徑向微動的重要影響因素，過大的接觸壓力會使過盈量增大，從而導致砂輪—軸的裝配體應力增大，降低砂輪的工作可靠性。同時較小的接觸壓力會增大砂輪輪轂與磨床主軸的脫離趨勢，同樣誘導徑向微動的發生。在轉速為8 000 r／min，不同的過盈量下，接觸壓力沿軸向的分布如圖5所示。從圖5可以看出最大接觸壓力在距離軸端70 mm處，即砂輪輪轂遠離軸向的一端，最小接觸壓力在距離軸向5 mm處。此處質量較大，故離心力較大，從而減小接觸壓力。

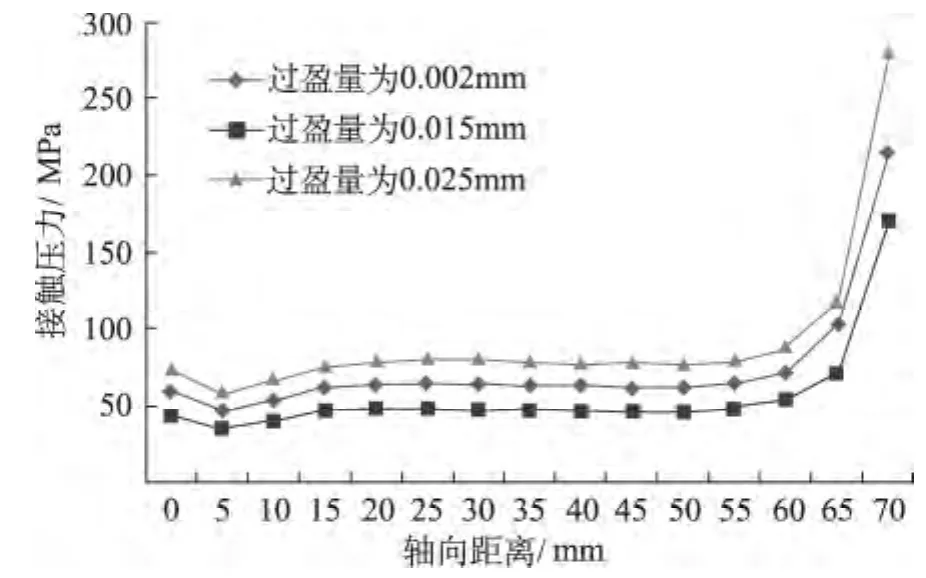
圖5 接觸壓力沿軸向隨過盈量變化曲線圖

3.2 轉速對過盈配合面特性的影響

在磨床主軸轉速為6 000 r／min，過盈量為0.01 mm的情況下裝配體應力云圖如圖6所示。裝配體最大等效應力為265 MPa，最大應力點在主軸的最右端。過盈配合面的最大等效應力與最大接觸壓力隨轉速變化的趨勢圖如圖7所示。

圖6 轉速為6 000 r／min，過盈量為0.01 mm時的裝配體應力云圖

從圖7可以看出，當磨床主軸轉速增加時，過盈配合面的最大合應力也逐漸增大，這是當主軸高速旋轉時產生了較大的軸向應力，從而導致裝配體的總體等效應力增加，但增大的幅值并不大。在最高轉速時，最大等效應力達到267 MPa，低于強度極限，故材料滿足強度要求。與最大等效應力不同的是，隨著轉速的增加接觸壓力逐漸減小，這是由于主軸高速旋轉時，將產生離心力，從而加大砂輪輪轂沿徑向向外脫離主軸的趨勢，由于此段的砂輪輪轂質量要大于主軸質量，故主軸的徑向變形要小于砂輪輪轂的徑向變形，繼而導致接觸壓力的減小。當主軸高速旋轉時產生的離心力將導致過盈配合面出現間隙，砂輪輪轂與磨床主軸分離而出現松脫現象，不僅影響扭矩的傳遞和砂輪的磨削功能，還增加砂輪的徑向跳動。

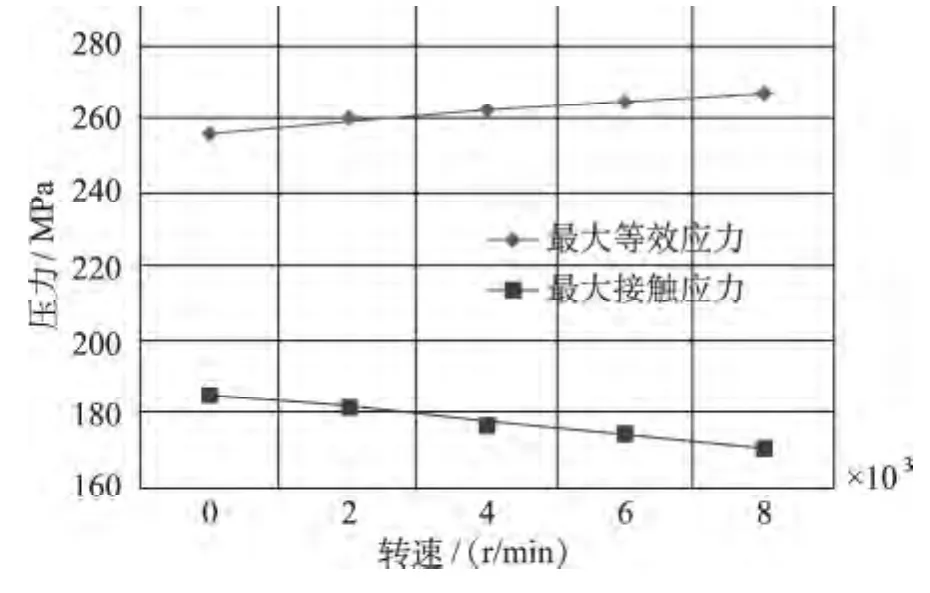
圖7 最大等效應力與最大接觸壓力隨轉速變化曲線

離心力對主軸和砂輪輪轂配合面過盈量的減小量可通過公式（1）求得［10］

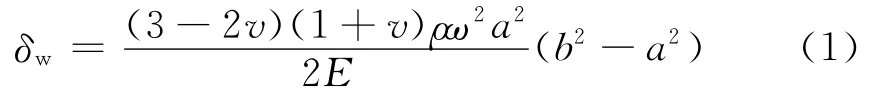
式中，v為主軸的泊松比；ρ為主軸密度；ω為角速度；E為泊松比；b為砂輪輪轂徑向位移（半徑方向）；a為配合軸端的徑向位移（半徑方向）。圖8是轉速為8 000 r／min，過盈量為0.01 mm時，主軸與砂輪輪轂的分離狀態圖。

圖8 主軸與砂輪輪轂的分離狀態

圖9為位移與轉速關系曲線圖，從圖中可以看出，隨著轉速的增大砂輪輪轂徑向位移和主軸的徑向位移也呈現出增大的趨勢，并且砂輪輪轂的位移要大于主軸的位移，這是因為此段砂輪質量大于此段主軸質量。但增大的幅值并不大，當主軸達到最高轉速8 000 r／min時，砂輪輪轂最大徑向位移僅為10.13μm，滿足砂輪磨削的精度。同時可以看出，在最高轉速時過盈量的減小量，僅為4.58μm。這是可以忽略不計的，從而說明了砂輪與主軸過盈裝配的合理性。

圖9 位移與速度關系曲線圖

3.3 摩擦系數對過盈配合面特性的影響

在轉速為8 000 r／min，過盈量為0.01 mm的情況下，最大等效應力與最大接觸壓力隨摩擦系數變化的規律曲線如圖10所示。從圖10可以看出，隨著摩擦系數的增大，最大等效應力與最大接觸壓力也呈現出增大的趨勢，但是增大的幅值并不高，且接觸壓力增大的趨勢越來越弱，當摩擦系數達到0.25時，最大接觸壓力基本不再發生變化了，從而可以得到，摩擦系數對最大等效應力及接觸壓力影響并不大。

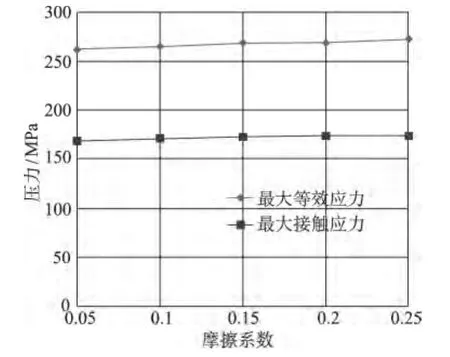
圖10 最大等效應力與最大接觸壓力隨摩擦系數變化曲線

4 結束語

（1）本文根據實際的裝配特點和約束情況，并根據有限元理論，通過有限元軟件ANSYS workbench建立了合理的有限元模型。

（2）研究表明過盈量的大小是引起最大等效應力及最大接觸壓力變化的主要因素。在進行強度計算時，應將其考慮進去，設置合理的過盈量不僅可以很好的傳遞扭矩，加大砂輪磨削的可靠性，還能夠滿足強度要求。

（3）當主軸高速旋轉時，過盈配合特性不僅與初始過盈量有關，也受主軸轉速影響。通過分析可知砂輪輪轂與主軸過盈的配合滿足轉速的要求。

（4）摩擦系數對最大等效應力及最大接觸壓力的影響并不大。

［1］ 白 釗，馬 平.FEA方法在電主軸階梯過盈聯結校核中的應用［J］.組合機床及自動化加工技術，2013，（12）：1－4.

［2］ 王 健.高速電主軸設計及主軸／刀柄接口聯接特性分析［D］.哈爾濱：哈爾濱工業大學，2009.

［3］ 馬 平，莫德云.電主軸階梯動態過盈量對主軸扭矩傳遞能力影響［J］.中國機械工程，2013，24（21）：2933－2937.

［4］ 許小強，趙洪倫.過盈配合應力的接觸非線性有限元分析［J］.機械設計與研究，2000，（1）：33－35.

［5］ 趙 華，何翠微，劉建新.機車輪對裝配應力的數值分析［J］.鐵道學報 ，1998，20（1）：45－51.

［6］ 賀地球，錢宇強.圓錐配合的非均勻應力場分析［J］.金屬礦山，2000，286（4）：54－55.

［7］ Zhao H.A numerical method for load distribution in threaded connections［J］.ASME J.of Mechanical Design，1996，118：274－279.

［8］ Zhao H.Analysis of load distributions within solid and hollow roller bearings［J］.ASME J.of Tribology，1998，120：1 34－139.

［9］ 林 輝，趙文禮.過盈配合的輪轂軸承芯軸有限元分析［J］.機械，2014，41（1）：27－31.

［10］張 松，艾 興.基于有限元的高速旋轉主軸過盈配合研究［J］.機械科學與技術，2013，23（1）：15－17.

［11］李 兵，何正嘉，陳雪峰.ANSYSWorkbench設計仿真與優化［M］.北京：清華大學出版社，2008.