基于MATLAB仿真的配網故障定位研究
胡錦輝(廣東電網有限責任公司江門供電局,廣東 江門 529000)
基于MATLAB仿真的配網故障定位研究
胡錦輝
(廣東電網有限責任公司江門供電局,廣東 江門 529000)
本文采用基于模型參數識別原理的遞推最小二乘法對小電流接地系統單相接地故障進行定位。利用MATLAB建立故障定位模型,并仿真經不同電阻接地。對故障時故障相母線電壓和故障線路電流進行采樣作為定位算法程序的輸入數據。利用電壓和電流數據求解算法下電感L的估計值,從而計算出故障點到保護安裝處的距離。由于篇幅有限,本文將直接給出直接解參數方程及最小二乘法兩種算法的仿真結果,通過比較來確定最小二乘法在故障定位中更具有可行性。
小電流接地系統;單相接地故障定位;模型參數識別;遞推最小二乘法
1 接地故障測距方法的研究現狀
故障測距方法從原理上可以分為三類:(1)通過數值計算進行精確求解;(2)行波法,以行波測量為基礎;(3)借助人工智能的方法,通過對特征信息的記憶達到擬和誤差最小。目前提出的故障測距技術主要有如下幾種:行波法、S注入法、五次諧波零序電場-磁場探測接地點法、加信傳遞函數法和阻抗法等。
阻抗法故障測距原理是假定線路為均勻線,在不同故障類型的條件下計算出故障回路阻抗或電抗與測量點到故障點的距離成正比,從而通過計算故障時測量點的阻抗或電抗值除以線路的單位阻抗或電抗值得到測量點到故障點的距離。
但配電網結構復雜,分支線、混合線路較多,故阻抗法不能簡單直接用于測距計算。為提高測距計算的準確度,本文對遞推最小二乘法在測距計算中的應用進行探討。
2 故障定位算法原理
線路對地電容對實際故障定位精度較大影響,考慮線路對地電容會增大計算量,增加定位的時間,但由于模型更接近實際,定位的準確性更高。
圖1為考慮線路對地電容的故障等效電路,電路圖中uA(t)為故障相母線電壓,uf(t)為故障點電壓,i(t)為故障線路電流。根據電壓電流關系可得:
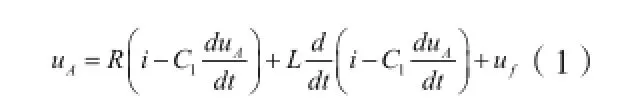
2.1 考慮線路對地電容遞推最小二乘法
遞推最小二乘法的基本思想是:
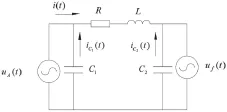
圖1 測距計算等效電路
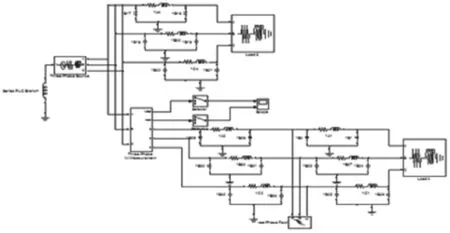
圖2 考慮對地電容接地系統仿真模型
新估計值=舊估計值+修正項
線性方程組zL=HLθ完成一次最小二乘法為
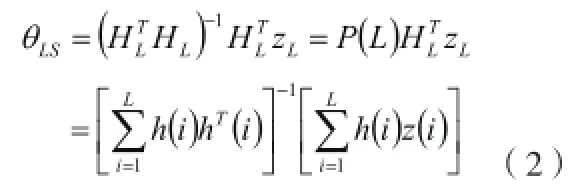
定義
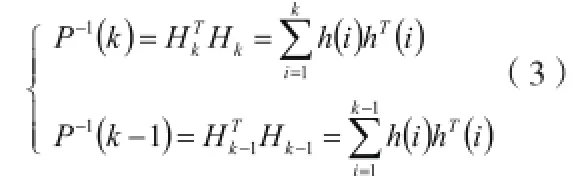
式中
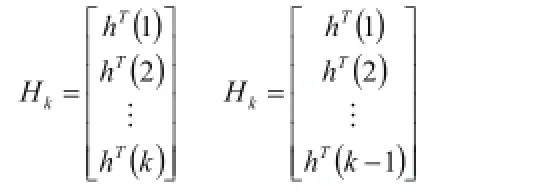
式中:h(i)是一個列向量,即HL的第i行的倒置,P(k)是一個方陣,它的維數取決于未知參數的個數。
P(k)的遞推關系為

設
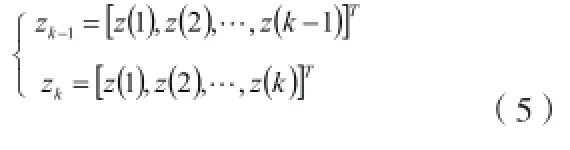
則
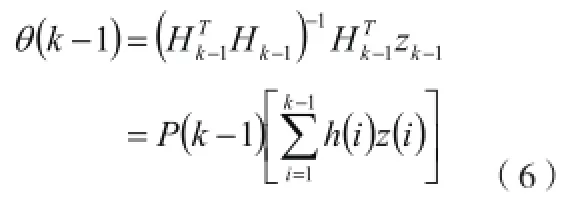
由此可得
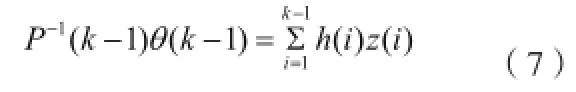
聯立上述式子可得(8)
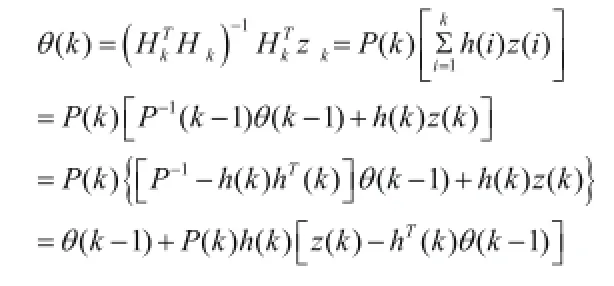
引進增益矩陣K(k),定義為
K(k)=P(k)h(k) (9)
則θ(k)= θ(k-1)+K(k)[z(k)-hT(k)θ(k-1)] (10)
把P(k)寫成P(k)=[P-1(k-1)+ h(k) hT(k)]-1(11)
利用矩陣反演公式(A+CCT)-1=A-1-A-1C(I+CTA-1C)-1CTA-1(12)
可得
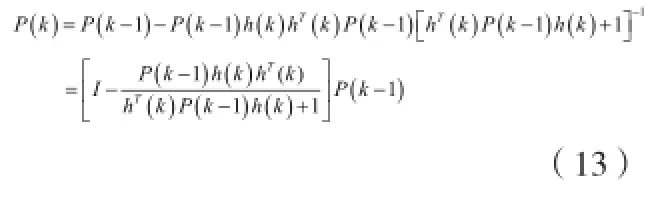
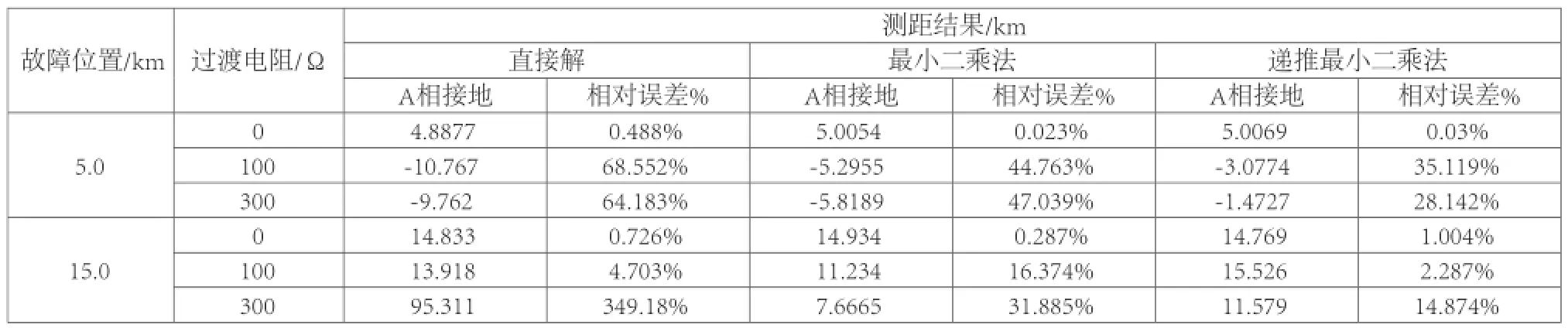
表1 考慮線路對地電容故障測距仿真結果
則
K(k)= P(k-1)h(k)[hT(k)P(k-1)h(k)+1]-1(14)
綜合上述式子可以得到最小二乘法遞推參數估計算法
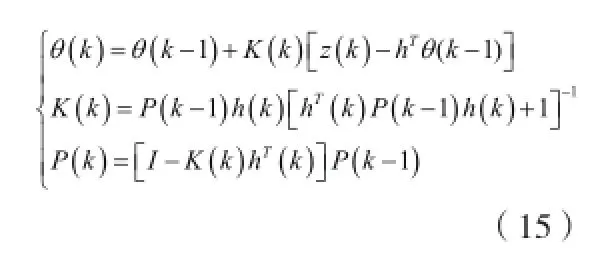
3 故障定位MATLAB仿真分析
建立線路模型來獲取需要的故障母線電壓和故障線路的電流,為算法計算提供數據。
圖2是采用MATLAB的Simulink環境構建的考慮線路對地電容單相接地故障仿真模型。
線路參數為R=0.45Ω/km,L= 0.9337mH/km,C=70.7nF/km線路長度為L1=18km,L2=23km。故障時間為0.01s~0.05s,采樣時間T=0.0001s。補償方式采用過補償,即(L為消弧線圈電感值,C為故障時產生電容電流的電容大小)。
將仿真采樣數據作為故障測距算法程序的初始數據進行仿真計算,下面也給出直接解參數方程和最小二乘法的計算結果。故障定位誤差采用相對誤差計算公式

結語
直接解參數方程的方法對于金屬性接地的準確性是比較高的,但隨著接地電阻的增大,準確就會隨之下降,可靠性不能滿足。在考慮線路對地電容的情況下,遞推最小二乘法的準確性比最小二乘法的準確性要高。
對于考慮線路對地電容的情況下,要保證測距的準確性,MATLAB仿真的采樣數據應該是在故障發生的暫態時刻。此時,消弧線圈的電感電流還沒有補償到故障線路電容電流,對計算用的電流數值產生影響。采樣的頻率越高,采樣的數據點越多,對于最小二乘法和遞推最小二乘方法的計算就越準確。
隨著接地電阻的增大,會使接地故障時的特征變得越不明顯,由于測量器件的測量誤差和精度問題,往往會使測距計算的結果不準確。
[1]黃彥全,肖建,李晉,等.最小二乘法在距離保護中的應用初探[J].繼電器,2004.
[2]劉家軍,李春舉,李文玲.在故障測距中應用故障分量電流的阻抗法研究[J].電氣化鐵道,2003.
TM769
A

