基于SOM神經網絡聚類的空調負荷聚合方法

許雅婧，黃小慶，曹一家，張志丹，戴麗麗

（湖南大學電氣與信息工程學院，長沙410082）

基于SOM神經網絡聚類的空調負荷聚合方法

許雅婧，黃小慶，曹一家，張志丹，戴麗麗

（湖南大學電氣與信息工程學院，長沙410082）

空調類負荷的準確建模對電力系統暫態分析影響較大。為研究日益增多的空調集群特性，提出了基于自組織神經網絡SOM（self-organizing feature map）聚類的空調負荷聚合建模方法。首先，通過靈敏度分析，提取對暫態分析最重要的幾個空調模型參數，利用層次分析法AHP（analytic hierarchy process）確定其權重；再通過帶權重訓練的SOM對空調負荷進行聚類；最后，簡化基于穩態模型等效變換的方法，對每一類空調進行聚合。算例表明，相比不聚類直接聚合，采用先聚類后聚合的方法對配電網中的空調負荷聚合，既可顯著提高模型仿真的精度，又為研究其他負荷的聚合提供了一種新思路。

空調聚合；自組織神經網絡；層次分析法；權重訓練

經濟發展和氣候變暖使得空調類（空調、冰箱）負荷在中心城市電網中的比重迅速增長[1]。據統計，夏季高峰時中國大中城市的空調負荷比重超過了30%～50%[2]。空調負荷具有特殊的無功-電壓特性，且啟、停時均會產生較大的功率沖擊，給城市電網的電壓穩定帶來不利影響，如1987年發生在日本東京的一次令人震驚的電壓崩潰事故，研究表明空調類負荷在事故中起很大的負面作用。因此，研究空調負荷的建模方法對于揭示其自身特性及預防其對電網電壓的不利影響具有現實意義。夏季空調比例較多是造成用電高峰的一個重要原因，研究空調負荷能夠為有效的規劃有序用電[3]、削峰填谷、節約能源提供有價值的依據。微電網相對主網總負荷較少，空調負荷的精確建模對于微電網的穩定運行與控制也有重要意義。

針對空調的特性及負荷模型，文獻[4]實測了單臺空調的停機、啟動特性及電壓擾動特性，對單臺空調采用Karlsson-Hill模型及指數函數建立非機理模型；文獻[5]針對空調未停機時及啟動時沿用文獻[4]中的模型分別建立空調群負荷的模型，但是Karlsson-Hill的非機理模型并不適用于暫態穩定分析的要求；文獻[6]通過空調特性實驗研究了單臺空調的啟動等4種運行特性并分別建立了其運行特性模型。動態負荷的合理建模對提高電力系統數字仿真準確度具有重要意義，但受電力系統數字仿真規模等因素限制，在仿真時對所有空調逐一建模是不現實的[7]，因此，有必要研究空調的聚合模型以模擬空調的行為特性。

此外，在配電網中空調種類繁多，不同的空調其負荷特性具有一定的差異性，試圖建立一個所謂“通用”模型描述所有空調的特性是不切實際的[8]，因此，有必要對空調先聚類后聚合。電力系統負荷特性聚類可歸為模式識別的問題。人工神經網絡具有學習速度快、分類精度高等優點，廣泛的應用于經典模式識別領域的聚類分析中[9-10]。由于過多的輸入參數會使計算產生冗余，且空調各參數對聚類的貢獻不同，故聚類的輸入向量的選取也很重要。文獻[11]提出基于滑差同調等值的理論對空調群負荷建模，但未涉及具體的分類過程。

針對上述不足，本文采用自組織神經網絡解決空調負荷特性的聚類問題。首先通過靈敏度分析提取對暫態分析重要的空調參數作為輸入向量；再用層次分析法確定權重；通過帶權重訓練的SOM對空調聚類；最后，采用簡化計算的穩態模型等效變換的方法將每一類空調進行聚合，并通過Simulink仿真驗證本文聚類及聚合方法的有效性。

1 空調基本特性及等值模型

空調啟動、運行時具有不同的動態特性，啟動時，空調的轉矩是初始轉矩的二次函數，而穩態運行時，空調負荷具有恒轉矩的特性[12]。當空調的端電壓降到額定電壓的0.6 p.u.以下時，空調會發生堵轉[13]，直到堵轉前1.2 s，空調都相當于恒轉矩負荷[12]。

在空調負荷中，消耗功率最大的是壓縮機，通常占到空調總功耗的90%以上，而壓縮機的動力來源于驅動其往返運動的電動機，因此與電動機具有相似的特性。壓縮機具有較小的慣性時間和快的電磁動態特性，所以用三階及以上的三相異步感應電動機模型能很好地反映空調壓縮機的性能[13]。因此，本文采用Simulink中提供的三相異步電動機建立未堵轉前空調負荷的模型，并設置輸出轉矩為恒定值以模擬空調壓縮機的恒轉矩特性。三相異步電動機的穩態等效電路如圖1所示。其中，定子阻抗Zs=Rs+jXs，轉子阻抗Zr=Rr/s+ jXr，勵磁阻抗Zm=jXm，s為轉差。

圖1 三相異步電動機穩態等效電路Fig.1Steady-state equivalent circuit of three-phase asynchronous motor

2 空調負荷聚類-聚合建模的流程

本文提出的基于SOM聚類的空調負荷聚合建模的工作流程如圖2所示。

步驟1將各空調的參數x=[Rs，Xs，Rr，Xr，Xm，s0，T，H]根據各自電動機基準容量標幺化并標準化，即初始化。其中，Rs、Xs為定子電阻、電抗，Rr、Xr為轉子電阻、電抗，Xm為勵磁阻抗，s0為穩定運行轉差，T為機械轉矩，H為慣性時間常數。

步驟2對空調負荷用SOM進行聚類。為減少參數冗余，提高神經網絡訓練效率，提取對暫態穩定分析重要的空調參數作為輸入向量x′，本文x′= [Rr，s0，H]；采用AHP法依據x′對聚類的貢獻大小，計算各輸入向量的權重向量w=[w1，w2，w3]；利用帶權重的SOM神經網絡將空調負荷聚類識別為n類，考慮實際情況以及使用方便，輸出類別n不宜過多，一般2≤n≤5。

圖2 基于SOM聚類的空調負荷聚合方法流程Fig.2Flow chart of aggregation of air conditioner load based on SOM clustering

步驟3將屬于同一類的空調負荷分別聚合。特別地，對每一類的空調進行聚合時，本文提出利用穩態模型等效變換的方法建立空調聚合模型。

3 基于SOM的空調聚類識別

3.1 自組織映射神經網絡

自組織映射（SOM）神經網絡是由芬蘭神經網絡專家Kohonen在1981年提出的，采用無監督的學習算法進行網絡訓練，具有學習速度快、分類準確、抗噪聲能力強等優點，因此在國內外的負荷聚類分析中得到廣泛應用[9-10]。

自組織映射神經網絡由輸入和輸出層2層神經元組成，輸入層中每一個神經元通過可變權值與輸出層各神經元相連，輸出神經元形成一個二維平面陣列。SOM神經網絡通過競爭算法完成學習過程，對競爭獲勝的神經元C及其周圍鄰域Nc內的神經元的權值進行調整，使得輸出節點保持輸入向量的拓撲特征。

3.2 空調聚類識別輸入向量的提取

一般來說，聚類過程在特征空間進行，樣本特征向量的選取相當關鍵，將決定整個分類結果的好壞[9]。本文為了給SOM網絡提供合適的輸入特征向量，采用靈敏度法分析空調參數中對暫態分析比較重要的參數，并選取為特征向量。

通常電網的頻率較為穩定，而電壓的變化受無功功率的影響較大，空調具有特殊的Q-V特性，當電壓明顯低于額定值時，無功功率隨電壓下降反而具有上升的趨勢，使電壓跌落更低。空調在啟動時會對電網產生4～6倍的有功、無功沖擊，對電網產生不良的影響。因此，通過考察空調參數變化對空調有功和無功的影響，分析某一參數對暫態仿真的影響。

為了定量分析空調參數θ在某一取值附近微小變化對空調有功和無功功率的影響，通過求解參數θ在該值時對空調功率的靈敏度?P/?θ及?Q/?θ來衡量。其中，空調參數是指空調的電氣參數、轉差s0、慣性時間常數H。

根據文獻[14]，負荷參數中對無功功率有較大影響的是s0和H，對有功功率有較大影響的是s0、Rr、H。基于此結論，本文選取空調參數中對暫態穩定分析影響較大的s0、Rr、H作為SOM的輸入特征向量，各輸入參數均依據各自電動機基準容量標幺化并標準化。特征向量的合理提取不但提高了空調分類的合理性，而且減少了SOM網絡的訓練時間。其拓撲結構如圖3所示。

圖3 基于SOM的空調負荷聚類識別Fig.3Air conditioner load clustering recognition model based on SOM

3.3 神經網絡權重的確定

由于各個特征向量對聚類的貢獻不同，因此有必要在訓練前確定各輸入向量的權重。層次分析法AHP（analytic hierarchy process）[15]是美國運籌學家Satty提出的一種對較為模糊或復雜決策問題使用定性與定量分析相結合的手段做出決策的簡易方法。本文用其確定準則權重。

比較m個元素對目標的影響，根據Satty判斷尺度建立m階判斷矩陣A，aij=Ci/Cj表示兩兩評價準則重要性的比，且aij〉0；aij=1/aij；aij=1。判斷矩陣的最大特征根λmax對應的特征向量歸一化后可作為權向量w=（w1，w2，…，wm）。

為了檢驗判斷矩陣的一致性，定義一致性指標為

為了衡量CI的大小，Saaty引入隨機一致性指標RI，見文獻[15]。定義一致性比率為

當一致性比率CR〈0.1時，認為判斷矩陣具有一致性，通過一致性檢驗，據此計算的權重值可以接受。

根據空調主導參數s0、Rr、H的靈敏度大小[14]確定其對暫態分析的重要度，則重要度的從高到低排序依次為：s0、H、Rr。同時，采用AHP中常用的9級標度法，由專家給它們形成的判斷矩陣的元素賦值。若求得的矩陣最大特征值可以通過一致性檢驗，則所得的特征向量即為表示參數s0、Rr、H重要性的權重向量w，具體結果為w=[w1，w2，w3]= [0.50.16670.3333]。在此，權重計算過程從簡，專家賦值見表1。

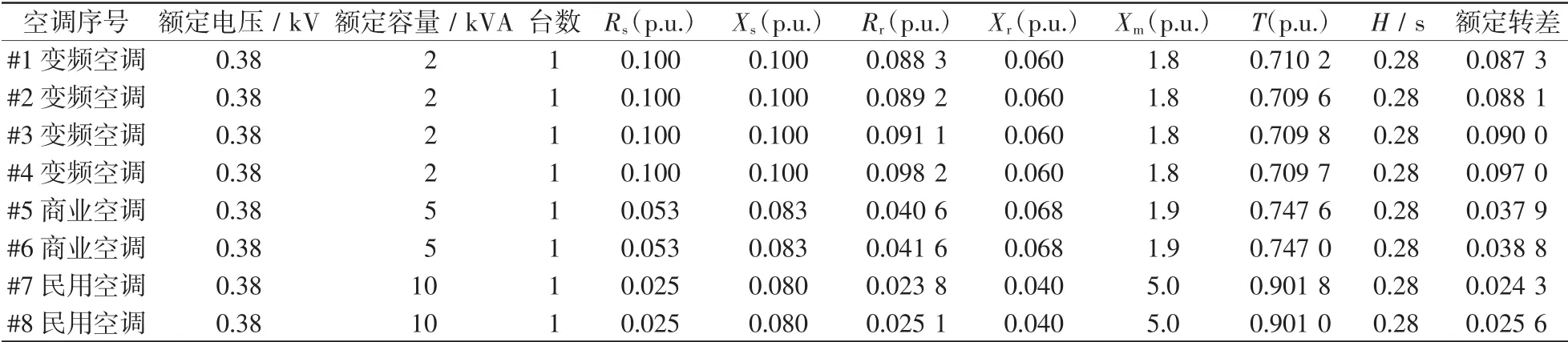
表1 隨機產生的8臺空調具體參數Tab.1Random parameters of 8 air conditioners

3.4 帶有權重的SOM網絡訓練

SOM網絡采用無監督學習方式，在訓練過程中，能夠根據輸入樣本的特征自動進行聚類。帶權重的SOM訓練具體步驟如下：

步驟1確定神經網絡結構。本文選取SOM神經網絡輸入層神經元數為3，每一神經元對應輸入特征向量的一個分量，即分別為空調負荷的3個輸入向量Rr、s0，H。輸出層神經元數為k。

步驟2初始化。對N個輸入神經元到輸出神經元的連接權重矢量mj賦予隨機的權值，其中mj=（μ1j，μ2j，…，μnj），j=1，2，…，k。

步驟3提供新的輸入樣本，本文的輸入變量為空調負荷的主要參數[Rr、s0、H]T，樣本為N個。輸入變量的矩陣為x(3×N)。

步驟4對輸入變量x賦予權重w=（w1，w2，…，wm），每個輸入變量更新為wx=（w1x1，w2x2，…，wmxm），m=3。

步驟5計算每個輸入樣本與每個輸出神經元j之間的歐式距離。

其中，距離最小的神經元c即為獲勝神經元。

步驟6對獲勝神經元c所連接的權向量及其幾何鄰域Nc（t）內的神經元，修正其權向量，即

式中，η（t）為可變學習速度，η（t）和Nc（t）鄰域都隨著時間而衰減。

步驟7提供新的學習樣本，從步驟3開始重復上述學習過程，直至所有樣本訓練完成。

訓練結束后，輸出編號一樣的神經元就代表了特征上相似的類別，可以劃分為同一類。

4 空調聚合模型

本文采用穩態等值電路計算聚合空調的等效參數，仿真采用Simulink，所求參數滿足Simulink暫態仿真參數的需求，其中電動機采用6階模型。需要計算的空調參數有：定子電阻Rs、電抗Xs，轉子電阻Rr、電抗Xr，勵磁阻抗Xm，轉差s0，機械轉矩T，慣性時間常數H。

4.1 聚合空調的等效電氣參數

空調的穩態等效電路如圖4所示。在保證同樣的電壓、電流時，等效電路可由圖4中3個阻抗的并聯代替[16]。

圖4 單臺空調的等效電路變換示意Fig.4Equivalent transformation circuit diagram of single air conditioner

考慮電機在堵轉時，轉差率s=1，則Zr=Rr+ jXr。由圖4的等效電路可得

式中：Zs、Zr、Zm分別為定子阻抗、轉子阻抗、勵磁阻抗；Zeq為等效阻抗，由式（5）可計算出Zeq的值。

將n臺空調并聯于同一母線上，則這些空調聚合后的等效電路如圖5所示。

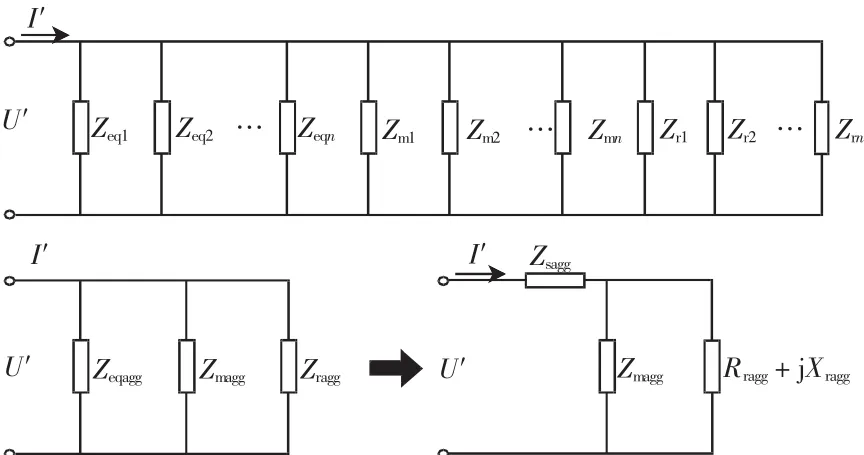
圖5 聚合空調的等效電路Fig.5Equivalent circuit of aggregated air conditioner

由聚合空調的等效電路可得

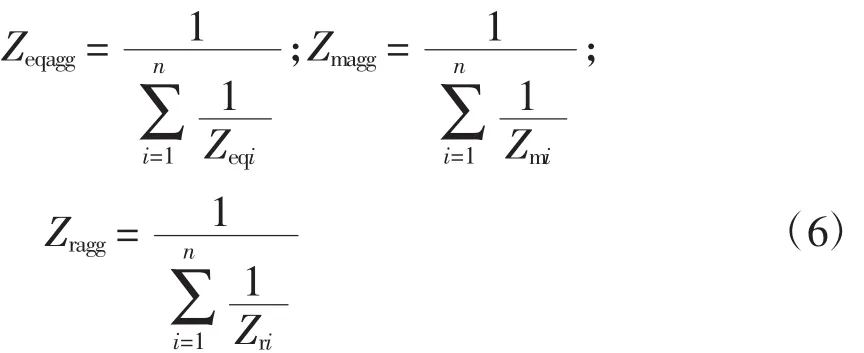
式中：Zmi、Zri、Zeqi為單臺空調的勵磁阻抗、轉子阻抗、等效阻抗，Zmi=jXmi，Zrir=Rri+jXri；Zmagg、Zragg、Zeqagg為各聚合空調的阻抗值。進而根據聚合空調等效變換電路及式（5）～式（6），可求得聚合空調的定子阻抗Zeqagg。

4.2 聚合空調的額定轉差

聚合空調額定轉差的確定可用以下2種方法。

（1）單臺空調的額定轉差為sNi，則額定運行時，電機的額定定子線電流（星形連接）為

式中：UN為空調的額定電壓；φNi為單臺空調的額定功率因數角；Zsi為各空調的定子阻抗；Zsi=Rsi+ jXsi，Zri=Rri/sNi+jXri；進一步可得出各空調在額定運行時的功率因數為cos φNi。

根據式（7），單臺空調的額定輸入功率PNini為

根據聚合空調的輸入功率等于n臺空調的輸入功率之和，可得聚合空調的額定輸入功率PNinagg：

從等效電路的定子端看進去，聚合空調的總阻抗為

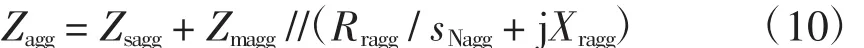
式中：Rragg、Xragg為聚合空調的轉子電阻、電抗；sNagg為待求的聚合空調額定轉差。

由式（10）計算聚合空調額定輸入功率PNinagg為

式中各值需取統一基準下的標幺值。

根據式（9）～式（11）可求聚合空調的額定轉差sNagg。此處相比文獻[16]簡化了額定輸入功率的計算過程。

（2）若已知單臺空調的額定容量為Sb，即

式中，Pin、Qin分別為單臺空調的額定輸入有功、無功功率。則有

根據式（13）可得

式中，Xp、Xsm、Xrm為引入阻抗，Xp=XsXr+XsXm+ XrXm，Xsm=Xs+Xm，Xrm=Xr+Xm。解式（14）就可求得聚合空調的額定轉差sNagg。需要說明的是，空調的額定容量Sb一般都是已知的，相比方法（1）中求PNinagg節省了復雜的計算過程，且通過對式（12）進行適當變形，只需解式（14）即可求得額定轉差，因此簡化了計算過程。

4.3 聚合空調的機械轉矩

單臺空調的額定輸出功率PNi為

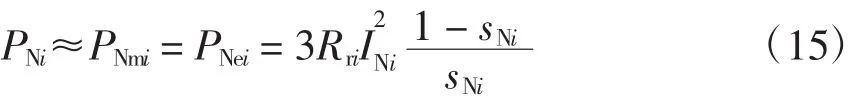
式中：PNmi、PNei分別為單臺空調的額定機械功率和電磁功率；Rri為各轉子電阻。

空調在正常運行時具有恒轉矩特性，機械轉矩T等于額定負載轉矩。則聚合空調的額定輸出功率PNagg為

聚合空調輸出的額定負載轉矩為

式中，nNagg聚合空調額定轉速，nNagg=ns（1-sNagg），ns為同步轉速。

4.4 聚合空調的慣性時間常數

若已知量為單臺空調的慣性時間常數Hi，則根據以額定轉速旋轉時的動能守恒[16-17]可得

式中，Hagg為聚合空調的慣性時間常數。

5 空調聚合模型有效性的仿真與驗證

為了驗證本文所提聚合方法的有效性，利用本文先分類后聚合建立的空調負荷模型，討論其參與配電網暫穩態的仿真結果。

考慮3種不同類型的空調負荷：變頻空調、商業中央空調、民用中央空調，其典型參數如表1所示[8]。本文假設配電網中空調的總數為8臺，其中這3種空調負荷比例分別為2∶1∶1，為符合實際情況，8臺空調的參數做如下隨機處理：由于實際空調的參數具有差異性，對主導電氣參數Rr取均勻隨機數，根據式（12）～式（17）計算每臺空調的轉差s0和轉矩T。因篇幅限制，這里僅給出典型參數。對空調依次編號，其中變頻空調編號為1～4，商業中央空調為5、6，民用中央空調為7、8。

不聚類時將所有空調聚合為1臺，參數見表2。為了計算方便，用本文分類方法將空調分為3類，結果為：1～4為第1類，5、6為第2類，7、8為第3類，與實際相符。

表2 三種類型的空調模型的參數及聚合空調模型的參數Tab.2Classic parameters of three types of air conditioners and aggregated air conditioners

將8臺空調并聯于同一母線，與聚合空調進行穩態和暫態仿真對比，采用Simulink進行兩種場景的仿真。

場景1穩態仿真，假設空調均運行于額定電壓380 V，從0 s正常啟動。圖6～圖7分別表示空調群和聚合空調模型穩態時的有功和無功功率。從圖中可以看出，聚合的空調模型能很好地反映多臺空調的穩態仿真結果，而聚合為3臺的結果與多臺空調的功率曲線基本重合，比直接聚合的結果更接近，提高了聚合模型的精度。

圖6 空調群及聚合空調穩態時的有功功率Fig.6Active power of several air conditioners and aggregated air conditioner in steady state

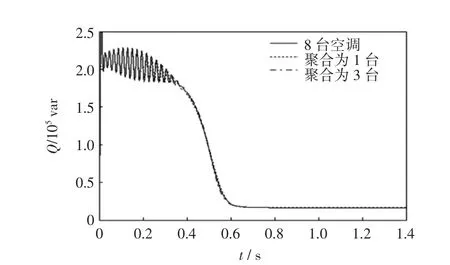
圖7 空調群及聚合空調暫態時的無功功率Fig.7Reactive power of several air conditioners and aggregated air conditioner in steady state

圖8 空調群及聚合空調暫態時的有功功率Fig.8Active power of several air conditioners and aggregated air conditioner of transient state

圖9 空調群及聚合空調暫態時的無功功率Fig.9Reactive power of several air conditioners and aggregated air conditioner in transient state

場景2暫態仿真，空調均從0 s正常啟動，在2 s時所有空調都斷電約8 rap的時間最后達到穩定。圖8～圖9分別表示空調群和聚合空調模型在暫態時的有功功率和無功功率。由圖可見，空調聚合模型能很好地反映多臺空調的暫態仿真結果，而分3類的聚合曲線與多臺空調的曲線基本重合，可以更好地模擬空調群的動態特性，提高了聚合模型的精度。

將空調負荷分為2～4類，依次進行暫穩態仿真，采用穩定后功率的相對誤差E對聚合結果進行評估，有功的相對誤差計算公式為

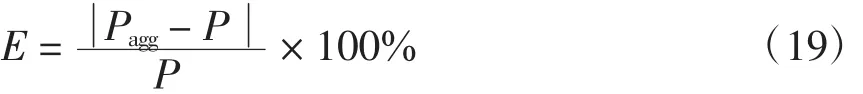
式中：Pagg為聚合空調的總有功功率；P為多臺空調的總有功功率。無功的相對誤差計算亦然。

穩定后的有功和無功功率以及相對誤差E見表3。由表3可見，不聚類的仿真結果相對誤差較大，這是因為配電網中空調種類較多且不同種類之間差異較大。在使用SOM分類后，隨著分類的增多，無功的相對誤差逐漸減小，并在某一點附近達到平穩。因本文采用有功功率平衡的原理進行聚合，所以有功功率的誤差很小，小于1%，無需單獨討論。本文分3類時相對誤差相比前幾類明顯的減少，分4類誤差減小的不多，故分3類在精度和計算復雜量上都有兼顧，是較理想結果。可見，分類并非越多越好，分類數需要在精度和計算復雜度之間取得平衡，經大量的仿真驗證，一般分3～5類為宜。實際中，若負荷中包含幾組特性上相差不大、總容量比較相近的空調負荷，分類時不同類的類內距相差不會很大，把它們等效為較少臺數的空調就可以滿足精度的要求，同時可以減小計算量。

表3 空調群及聚合模型達到穩態后運行情況對比Tab.3Steady-state operating conditions comparison of air conditioner group and aggregated air conditioner

6 結語

空調無功特性對配電網電壓穩定性影響較大，精確的空調負荷模型為電力系統仿真的精度提供保證。針對空調負荷的差異性，本文提出了基于自組織神經網絡聚類的空調負荷聚合建模方法。首先，通過靈敏度分析，選取對暫態分析影響較大的空調參數作為輸入向量，利用帶權重訓練的SOM神經網絡對空調負荷聚類；然后采用并簡化穩態模型等效變換的方法將同一類空調聚合。仿真表明采用SOM聚類-聚合方法，相比不聚類直接聚合，顯著提高了空調聚合模型的精度，能更好地模擬空調群的動態特性。本文提出的空調負荷聚類-聚合方法為研究空調的集群特性及其對電壓穩定性的影響奠定了基礎，為研究其他負荷的聚合提供一種新方法。

[1]李娜，褚曉東，張文，等（Li Na，Chu Xiaodong，Zhang Wen，et al）.考慮參數空間差異的多區域空調負荷聚合模型（Aggregation model of multi-zone air conditioning load considering spatial differences of parameters）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2012，24（5）：19-24.

[2]黎燦兵，尚金成，朱守真，等（Li Canbing，Shang Jincheng，Zhu Shouzhen，et al）.氣溫影響空調負荷的累積效應導致能耗的分析（An analysis of energy consumption caused by air temperature affected accumulative effect of the air conditioning load）[J].電力系統自動化（Automation of Electric Power Systems），2010，34（20）：30-33.

[3]鐘海旺，夏清，黃媚，等（Zhong Haiwang，Xia Qing，Huang Mei，et al）.降低網損和消除阻塞的有序用電模式與方法（A pattern and method of orderly power utilization considering transmission loss reduction and congestion elimination）[J].電網技術（Power System Technology），2013，37（7）：1915-1921.

[4]徐群，劉剛，李育燕，等（Xu Qun，Liu Gang，Li Yuyan，et al）.單臺空調負荷動態特性分析與建模（Characteristic analysis and modeling of a single air conditioner load）[J].高電壓技術（High Voltage Engineering），2006，32（11）：127-130.

[5]李育燕，陳謙，黃文英，等（Li Yuyan，Chen Qian，Huang Wenying，et al）.空調群負荷動態特性分析與建模（Dynamic characteristics and modeling of air conditioner loads）[J].高電壓技術（High Voltage Engineering），2007，33（1）：66-69，77.

[6]鄭競宏，朱守真，王光，等（Zheng Jinghong，Zhu Shouzhen，Wang Guang，et al）.空調負荷運行特性研究及建模（Key characteristics and modeling of air conditioner load）[J].中國電機工程學報（Proceedings of the CSEE），2009，29（10）：67-73.

[7]張紅斌，湯涌，張東霞，等（Zhang Hongbin，Tang Yong，Zhang Dongxia，et al）.考慮配電網絡的感應電動機負荷模型聚合方法研究（Study on aggregation of induction motors with distribution network）[J].中國電機工程學報（Proceedings of the CSEE），2006，26（24）：1-4.

[8]章健.電力系統負荷模型與辨識[M].北京：中國電力出版社，2007.

[9]張紅斌，賀仁睦，劉應梅（Zhang Hongbin，He Renmu，Liu Yingmei）.基于KOHONEN神經網絡的電力系統負荷動特性聚類與綜合（The characteristics clustering and synthesis of electric dynamic loads based on Kohonen neural network）[J].中國電機工程學報（Proceedings ofthe CSEE），2003，23（5）：1-5，43.

[10]代倩，段善旭，蔡濤，等（Dai Qian，Duan Shanxu，Cai Tao，et al）.基于天氣類型聚類識別的光伏系統短期無輻照度發電預測模型研究（Short-term PV generation system forecasting model without irradiation based on weather type clustering）[J].中國電機工程學報（Proceedings of the CSEE），2011，31（34）：28-35.

[11]鄭競宏，朱守真（Zheng Jinghong，Zhu Shouzhen）.基于滑差同調等值的空調群負荷建模（Slip coherency based approach for air conditioning load modeling）[J].電力系統自動化（Automation of Electric Power Systems），2008，32（16）：11-15.

[12]Sanhueza S M R，Tofoli F L，de Albuquerque F L，et al.Analysis and evaluation of residential air conditioners for power system studies[J].IEEE Trans on Power Systems，2007，22（2）：706-716.

[13]Shaffer J W.Air conditioner response to transmission faults [J].IEEE Trans on Power Systems，1997，12（2）：614-621.

[14]鄭競宏，李康，朱守真（Zheng Jinghong，Li Kang，Zhu Shouzhen）.暫態穩定分析中負荷模型主導參數研究（Dominant parameters of load model in transient stability analysis）[J].電力自動化設備（Electric Power Automation Equipment），2009，29（9）：1-6.

[15]陳慶前，余暢，章激揚，等（Chen Qingqian，Yu Chang，Zhang Jiyang，et al）.層次分析法在孤島微網綜合評價中的應用（Application of analytic hierarchy process in comprehensive evaluation of island microgrid）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2013，25（3）：133-137.

[16]Franklin D C，Morelato A.Improving dynamic aggregation of induction motor models[J].IEEE Trans on Power Systems，1994，9（4）：1934-1941.

[17]Karakas A，Fangxing Li，Adhikari S.Aggregation of multiple induction motors using MATLAB-based software package[C]//IEEE/PES Power Systems Conference and Exposition.Seattle，USA，2009.

Aggregation of Air Conditioner Load Based on Self-organizing Feature Map Neural Network

XU Yajing，HUANG Xiaoqing，CAO Yijia，ZHANG Zhidan，DAI Lili
（College of Electrical&Information Engineering，Hunan University，Changsha 410082，China）

The accurate modeling of air conditioner loads has significant effect on the transient analysis of power systems.To investigate the modeling and characteristics of a group of air conditioners，this paper presents a new method for aggregation of air conditioners，taking into account load clustering based on self-organizing feature map（SOM）.First，several load parameters are chosen by sensitivity analysis as input vectors which are important in transient stability analysis；weight to each vector is assessed by analytic hierarchy process（AHP）；and air conditioners are classified into different types via SOM.Last each type of air conditioners is aggregated with simplified steady state model equivalent method.The results indicate that the method in this paper can not only improve the simulation precision of air conditioners in distribution network obviously，but also contribute to the investigation of other load aggregation.

air conditioner aggregation；self-organized neural network；analytic hierarchy process（AHP）；assess weight

TM74

A

1003-8930（2015）11-0026-08

10.3969/j.issn.1003-8930.2015.11.005

許雅婧（1990—），女，碩士研究生，研究方向為空調負荷的建模、配電網仿真。Email：deliaxyj@163.com

2014-04-04；

2014-07-14

國家高科技研究發展計劃（863計劃）資助項目（2012AA050217）；國家電網公司重大項目（KJ[2011489]）

黃小慶（1981—），女，通信作者，博士，講師，研究方向為彈性負荷與電網的相互關系研究、微電網。Email：huang_xq@126.com

曹一家（1969—），男，教授，博士生導師，研究方向為電力系統優化與控制、進化計算與計算智能、智能控制系統與決策。Email：yijiacao@zju.edu.cn