基于相圖分割的Duffing混沌系統狀態判定方法

高振斌，孫月明，李景春

（1.河北工業大學電子信息工程學院，天津 300401；2.國家無線電監測中心，北京 100037）

基于相圖分割的Duffing混沌系統狀態判定方法

高振斌1，孫月明1，李景春2

（1.河北工業大學電子信息工程學院，天津 300401；2.國家無線電監測中心，北京 100037）

判別Duffing混沌系統所處的狀態是采用Duffing混沌振子進行微弱周期信號檢測的關鍵問題．本文針對系統在混沌和大周期兩種狀態相圖的明顯區別，提出了一種基于相圖分割的系統狀態判定方法．該方法首先在相圖中做一簡單閉合區域，進而通過統計相軌跡點處于區域外的數量來識別系統的狀態．給出了實現該方法的主要步驟，并從微弱信號檢測成功率和運算復雜度的角度進行了分析．實驗結果表明該方法可用于30dB信噪比下弱正弦信號的檢測，并且硬件實現簡單．

微弱信號檢測；混沌；Duffing振子；相圖分割；信噪比

0 引言

由于混沌系統具有對微弱信號敏感而對噪聲免疫的特性，它在微弱信號檢測領域得到了廣泛的關注，開辟了新的應用空間．自1992年BrownR等人[1]首次提出了運用Duffing振子對初值敏感這一特性設計傳感器的方法以來，混沌理論不斷得到改進和發展．1997年，王冠宇等人[2-3]研究了Duffing振子在微弱信號檢測方面的應用，實現已知頻率下信號幅度的測量，并把可以檢測的信噪比范圍延伸到為26dB，對這一領域的發展起到了推動作用．之后，哈爾濱工業大學的聶春燕[4]又對Duffing振子陣列掃描的方法進行了研究，以此測量微弱正弦信號的幅值、相位、頻率等參數，獲得較好的效果．

由此可知，Duffing混沌系統在微弱信號檢測中領域具有很大優勢，提供了與傳統檢測方法不同的檢測途徑．實際應用中，混沌系統狀態的準確判定是Duffing振子成功用于微弱信號檢測的關鍵．傳統的時序圖法不利于計算機自動處理，而Lyapunov指數法又易于受到噪聲的影響．本文利用Duffing振子系統在狀態變化前后相軌跡的明顯差別，提出了一種基于相圖分割的微弱信號檢測方法，并通過計算說明其可行性．

1 信號檢測與狀態判別原理

1.1 Duffing振子信號檢測原理

根據已有的研究成果，本文采用和文獻[5]相同的Duffing振子檢測系統模型[5]

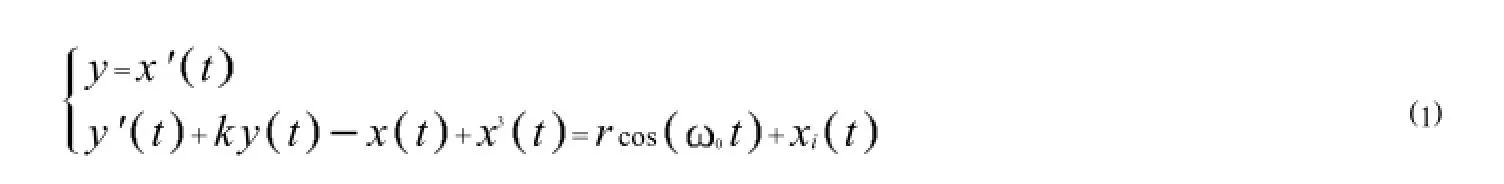
其中：k是阻尼比；χt+χ3t是非線性恢復力；cos0t是周期性策動力；χit為待測信號．

由混沌理論可知，沒有待測信號χit時（χit=0），在k固定的情況下，從0逐漸增大的過程中，方程的解所形成的相空間軌跡會依次表現為同宿軌道、倍周期分岔軌道和混沌狀態[4]．且當增大到由混沌轉向大周期的臨界值d時，軌跡會突然發生變化，從混沌狀態轉向大周期狀態，如圖1所示．

依據這個特點，可以得到使用混沌系統檢測微弱正弦信號的原理：如果把系統的策動力的幅值設為略小于臨界值d，使混沌系統處于臨界狀態．然后將待測信號χit輸入系統，如果系統的相軌跡從混沌狀態變為大尺度周期狀態，就說明待測信號中包含有與內策動力信號頻率相同的正弦信號．

基于這一原理檢測微弱正弦信號時，需要解決的關鍵問題是如何區分系統是處于混沌狀態還是大周期狀態．由于待測信號中存在噪聲，相圖中的軌跡曲線變得模糊．直接觀察系統相軌跡圖判別系統狀態的傳統方式，雖然簡潔直觀，但不宜于在計算機上或電路上實現自動判斷．時序圖法可通過示波器一次輸出多個信號狀態，而混沌狀態和大周期狀態所對應的時序波形不同，比較即可區分，效率確實得到了提高，但由于系統在臨界狀態下時序波形多樣，難以分辨，檢測效果仍不理想．相對而言準確性高的Lyapunov指數法經過數值計算，以定量指標作為標準，分析軌跡趨勢，判斷運動狀態，但原理與計算方法都較為復雜，并且受噪聲影響較大．針對這一問題，本文采用相圖分割的方法判別系統狀態，以實現微弱信號檢測目的．

1.2 基于相圖分割的系統狀態判別方法

由于Duffing振子系統在混沌狀態和大周期狀態時系統相圖截然不同，如果在其相對規則的環狀軌道內設置一個盡可能大的封閉區域，那么大周期狀態下軌跡點主要集中在區域外，混沌狀態下部分軌跡點落在區域內．通過統計相軌跡點處于區域外的數量，就可以判定相系統的狀態．

注意到Duffing振子的相圖特征，相圖分割法的基本思路是：在Duffing振子的二維相圖中做出一封閉區域，把相軌跡圖中所有點分為域內點和域外點2部分，域外點占總軌跡點數的比例越大，說明系統越接近大周期狀態．具體實現步驟為：1）在Duffing振子的規則環狀軌道內建立一盡可能大的不與該軌道相交的封閉區域，并且邊界線方程要取的盡量簡單些．2）統計相軌跡在區域內和區域外的點，并求出區域外的點數No占總點數Nt的比值Nr=No/Nt．3）對輸出結果的解釋是：比值足夠大，說明點主要集中在區域外，符合大周期狀態特點，判定輸入中存在正弦信號．

根據實現步驟，本文選擇方形區域這種非常容易實現的方式，即方域分割，邊界線如圖2所示，邊界線方程為

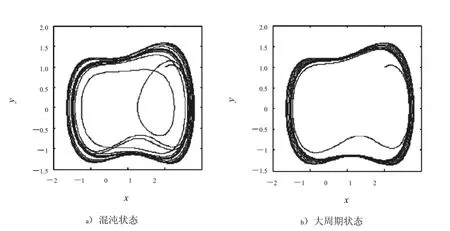
圖1 混沌狀態和大周期狀態Fig.1 Thechaoticstateandperiodicstatus

式中：R為方形區域的邊長，其選取應滿足不與環形軌跡相交并且要使得方形區域盡可能大．

2 信號檢測的可行性與可實現性分析

2.1 可行性實驗研究

由于Duffing方程為非線性方程,它不存在解析解,故只能依靠計算機數值計算來求出它的解．計算中采用定步長四階龍格-庫塔方法對Duffing方程進行求解．

根據混沌系統信號檢測理論，當周期策動力的頻率與待測信號中正弦信號的頻率相同，即0=20時，系統由混沌狀態轉為大周期狀態，此時，區域外的點數No占總點數Nt的比值Nr取最大值．

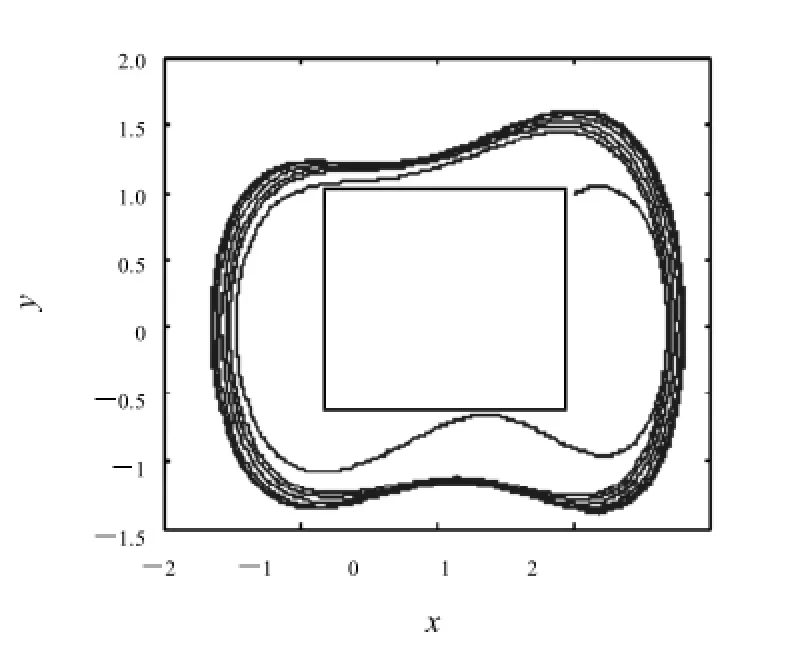
圖2 方域分割示意圖Fig.2 Thedomainsegmentationdiagram

不同信噪比下計算的結果如圖3所示．圖中橫坐標為信號搜索使用的系統周期策動力角頻率0，縱坐標為該頻率下相軌跡中方域外的點占總的相軌跡點數的比值Nr．圖3a）、圖3b）給出了信噪比為10dB和20 dB的條件下的結果．可以看出，比值Nr最大時對應的0與待測信號中正弦信號頻率相同，符合理論預測；圖3c）、圖3d）都是信噪比為30dB時得到的計算結果，但圖3c）所示跟理論預測相符，能檢測到信號，圖3d）所示不符合理論預測，檢測失敗．

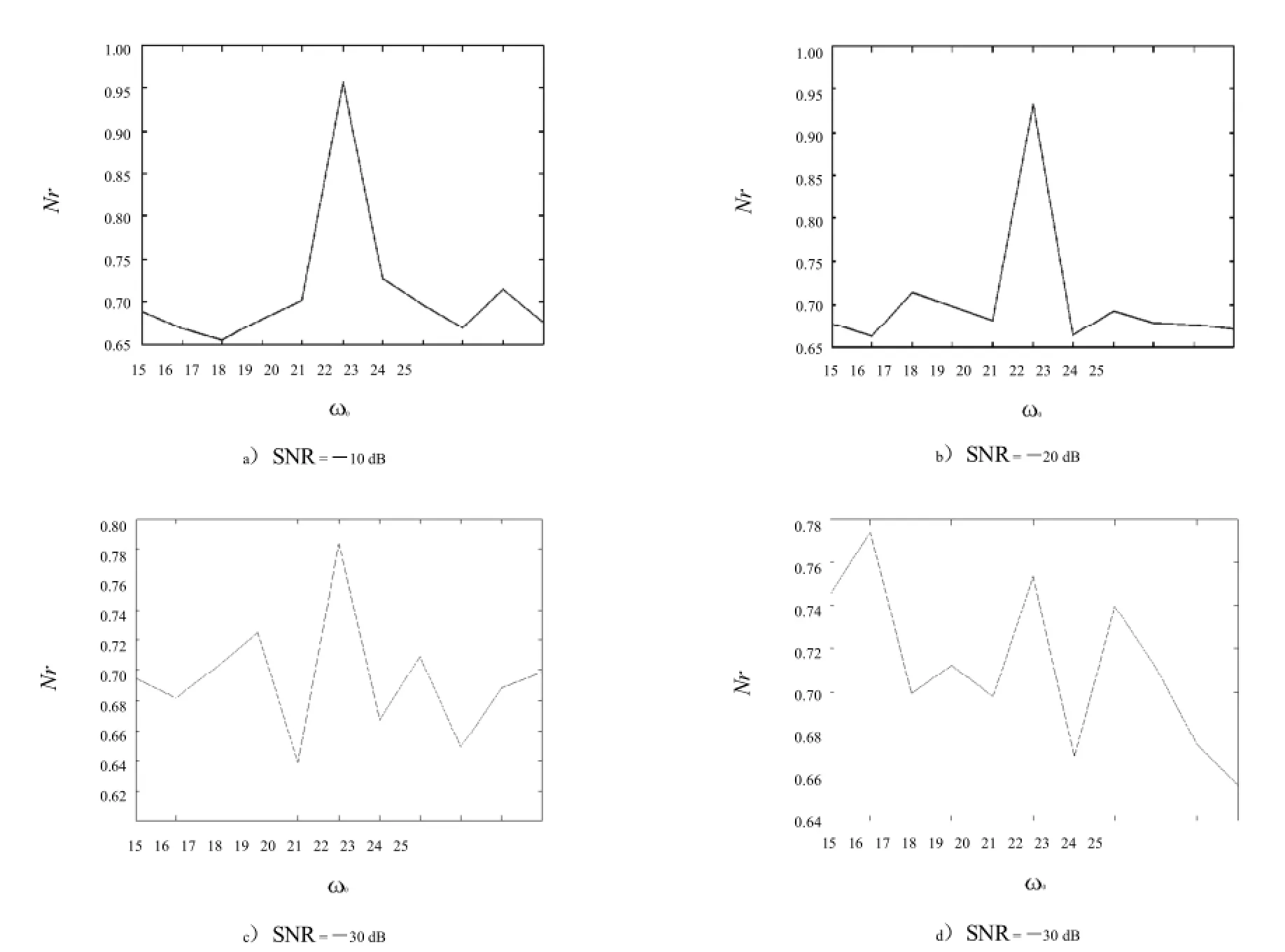
圖3 單次搜索時軌跡圖中方域外軌跡點所占比例Fig.3 Thepercentageofthepointsthatoutsidethesquareareainasinglesearch

這是因為在仿真計算過程中，噪聲是隨機產生的．由于噪聲的隨機性，相同信噪比條件下的噪聲信號也會有所不同，單次檢測結果出現偶然性．為了使檢測結果正確可靠，在同一信噪比下重復上述過程，進行多次實驗，再統計各個搜索頻率下得到最大Nr的次數Pi，

Pi=第i頻率下Nri大于其他各頻率下Nr的次數/總試驗次數

Pi即判定輸入中有該頻率正弦信號的概率．如果某一頻率下的概率值Pi明顯大于其他頻率點，則可以認為輸入中有該頻率的正弦信號，具體方法如下．

取實驗次數為500，方域分割檢測微弱信號的實現步驟為：

1）根據設定的參數，依次選取0dB到37dB信噪比的待測信號輸入到檢測系統，統計方域內、外點數，得到0=15，16，17，18，19，20，21，22，23，24，25的11個頻率點下，相應相軌跡圖中方域外的軌跡點占總軌跡點數的比值Nri．

2）求取Nri最大值對應的0．將該頻率點得到最大Nri的次數Ci加1．

3）重復上述過程500次，求各頻點下得到最大百分比的次數Ci，除以總實驗次數500，得到被判定輸入中包含該頻率正弦信號的概率Pi．

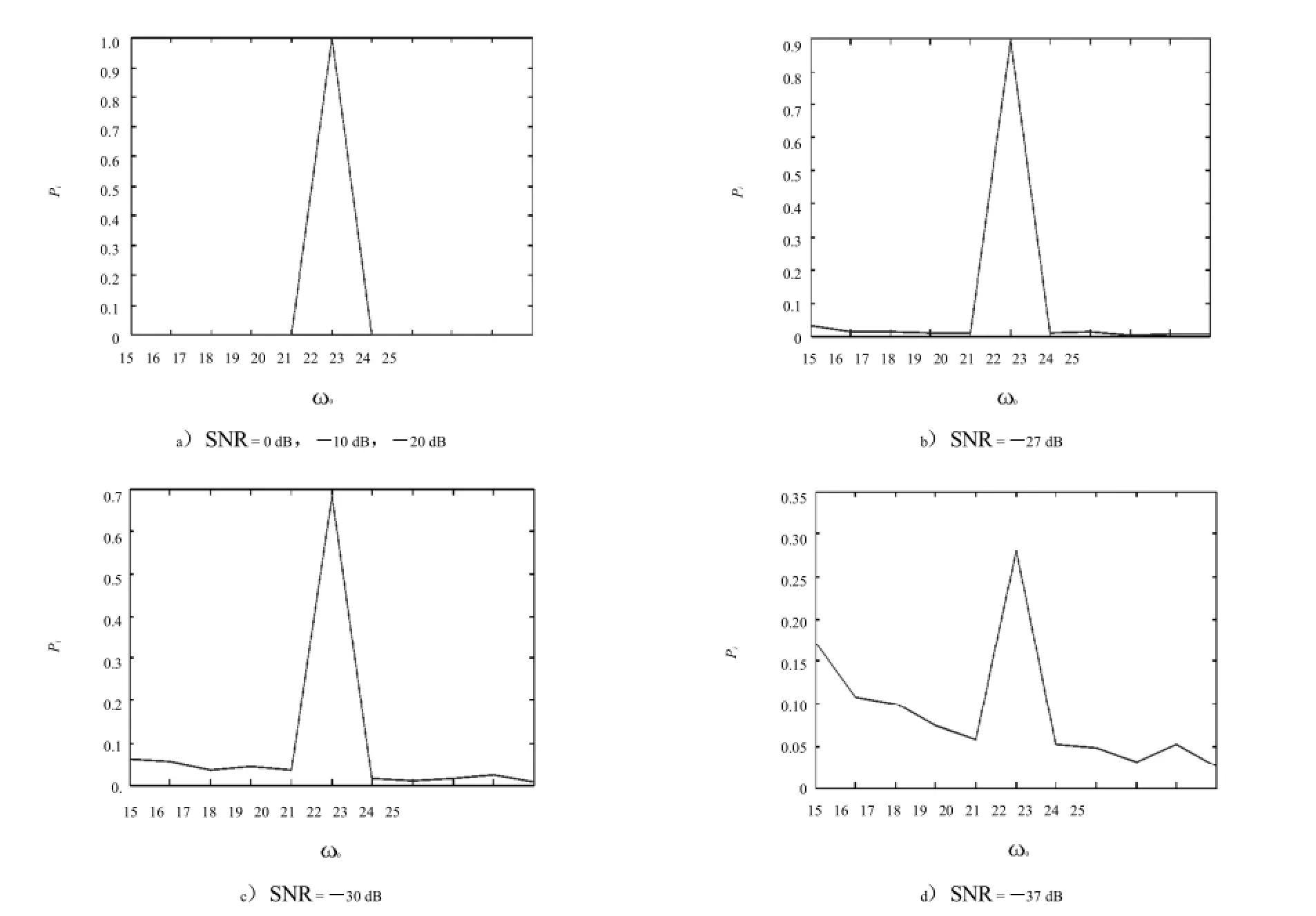
圖4 不同信噪比下信號檢測結果Fig.4 Thesignaldetectionresultunderdifferentsignal-to-noiseratio

表1 方域分割法不同信噪比下的信號檢測結果Fig.1 The signal detection resultsunder differentsignal-to-noise ratio

由表1可以看出，在信噪比取值為0dB，10dB，20dB時，Nri最大值對應的0全部與待檢信號頻率i相同，即單次檢測成功的概率為100%，說明信噪比較高的情況下方域分割法的檢測性能很好．降低待測信號信噪比至27dB，雖然Nri最大值對應頻率0i的次數不為0，但其僅為總次數的1.8%，但檢測效力依然較高．進一步降低信噪比至30dB，從圖4c）中可以看到0i時Pi較之前波動的幅度增大，最大達到了5.52%．當信噪比降為37dB時，0=15，16，……，25各頻率點對應的Pi分別為12.4%，12.4%，10.4%，7%，6.4%，25.4%，5.8%，6.8%，5.8%，3.2%，4.4%，但在0=i時Pi=25.4%，大于其他頻率下Pi的取值，而且區別比較明顯，可以認為輸入中含有該頻率的正弦信號．因此，方域分割法能用于信噪比大于30dB時信號檢測．在信噪比更低時，檢測性能逐漸變差，但通過多次檢驗仍可以推斷出輸入中可能含有某頻率分量的信號．

2.2 可實現性分析

在使用數字電路實現基于混沌振子的信號檢測系統中，為了節省資源，一般使用歸一化定點數進行運算．為了統計方域外的軌跡點數，需要把軌跡點坐標（x,y）中x和y的值與閾值進行比較，x、y中任何一個大于閾值則說明此軌跡點在方域外．對方域外軌跡點的個數進行記數即可判定系統狀態．方域分割的實現結構如圖5．

判別流程具體為：

1）將算法實現過程中求解所得到的軌跡點的坐標（x,y）分別與設定的閾值進行比較，當x,y的絕對值大于閾值時，比較器輸出為'1'．

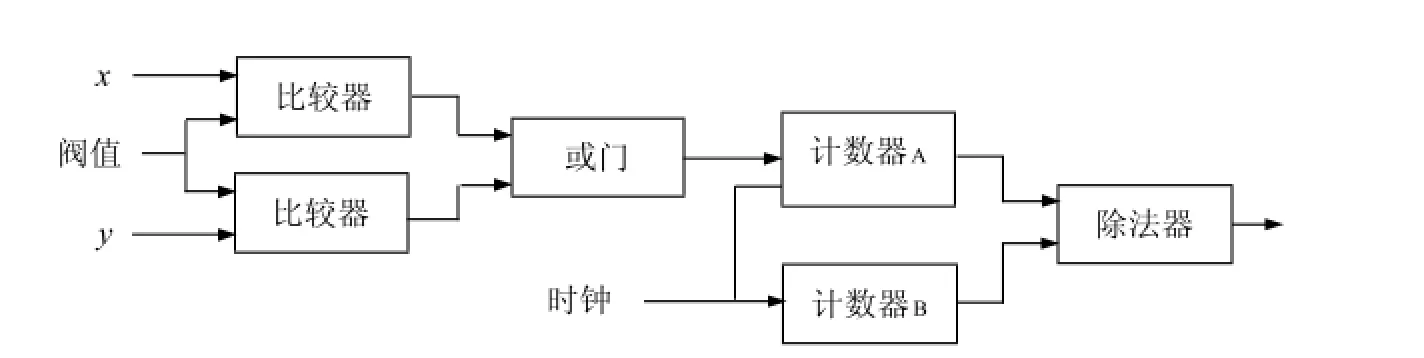
圖5 方域分割實現框圖Fig.5 Blockdiagramofthesquaredomainsegmentation

2）兩個比較器的輸出經過或門給到計數器A的計數使能端，當使能端為'1'時計數器A計數．

3）計數器A記錄方域為軌跡點的個數，計數器B記錄所有軌跡點的個數．

4）計數得到的值通過除法器，得到的即為方域外點所占百分比．

需要說明的是，在使用定點數運算時可以簡化比較器電路，只對部分有效位進行比較．比如可以只比較整數部分是否大于1，或只判斷其中某一位為'1'即可．另外，在每次循環計算的輸入數據個數一定時，計數器B可以省略，而且也不需要再進行除法運算．因此，方域分割法判定系統混沌狀態的實現電路較為簡單．

3 結束語

本文根據Duffing振子混沌系統在混沌狀態和大周期狀態下相軌跡的明顯差別，提出了基于相圖分割的微弱正弦信號檢測方法．在輸入信噪比優于20dB時，通過一次檢測即可判定輸入信號的頻率，檢測效果良好．在輸入信噪比更低時，可通過多次檢測求概率的方法判定輸入中含有某頻率成分的信號．從硬件實現的角度來看，方域分割法判定系統狀態僅需要比較器、計數器和除法器，且比較器可簡化，除法器可省略，比較易于工程實現．在工程實際中，可以根據具體條件，選擇合適的實施方案．

[1]BrownR，ChuaL，PoppB．Issensitivedependenceoninitialconditionsnature'ssen-sorydevice[J]．InternationalJournalofBifurcationandChaos，1992，2（1）：193-199．

[2]王冠宇，陶國良，陳行，等．混沌振子在強噪聲背景信號檢測中的應用[J]．儀器儀表學報，1997，18（2）：209-212．

[3]王冠宇，陳大軍，林建亞，等．Duffing振子微弱信號檢測方法的統計特性研究[J]．電子學報，1998，26（10）：38-44．

[4]聶春燕，石要武，劉振澤．混沌系統測量nV級正弦信號方法的研究[J]．電工技術學報，2002，17（5）：87-90．

[5]王雅曼．弱信號檢測技術研究[J]．科技創新導報，2011（7）：13-14．

[責任編輯 代俊秋]

AmethodforDuffingchaoticsystemstatusidentificationbasedonphasediagramssegmentation

GAOZhen-bin1，SUNYue-ming1，LIJing-chun2

(1.SchoolofElectronicandInformationEngineering,HebeiUniversityofTechnology,Tianjin300401,China;2.TheStateRadioMonitoringCenter,Beijing100037,China)

IntheweakperiodicsignaldetectionsystemswhichuseDuffingchaoticoscillator,thekeyproblemishow todiscriminatethestateofDuffingchaoticsystem.Inview oftheobviousdifferencesbetweentwokindsofsystemphasediagrams,chaosandlargecycle,anewsystemstatusdeterminationmethodthatbasedonthephasediagramsegmentation isproposed.Bymeansofmakingasimpleareainthephasediagram,thepointsonthephasetrackareseparatedintotwoparts,andthenthestateofthesystemcanbededucedby identifyingwhichareathepointsaremainlylocatedin.Themainstepsofthemethodaregiven.Thecorrectrecognitionrateandthecomputationcomplexityareanalyzed.Itshows thatthismethodisnotonlyfeasibleforweaksinusoidalsignaldetectingwith 30dBsignal-to-noise-ratio,butalsosimpleforimplementation.

weaksignaldetection;chaos;Duffingchaoticoscillator;phasediagramssegmentation;signaltonoiseratio

TN911.23

A

1007-2373(2015)01-0023-05

10.14081/j.cnki.hgdxb.2015.01.005

2014-09-28

國家自然科學基金（61139001）

高振斌（1973-），男（漢族），副教授，Email：gao-zb@163.com．