基于激光跟蹤儀的六自由度模塊化機器人運動學標定*

王艷孟，石成江，王殿君，劉淑晶，李 強，張義萬

(1.遼寧石油化工大學 機械工程學院，遼寧 撫順 113001；2.北京石油化工學院 機械工程學院，北京 102617)

基于激光跟蹤儀的六自由度模塊化機器人運動學標定*

王艷孟1，石成江1，王殿君2，劉淑晶2，李 強2，張義萬1

(1.遼寧石油化工大學 機械工程學院，遼寧 撫順 113001；2.北京石油化工學院 機械工程學院，北京 102617)

在充分調研國內外機器人標定方法的基礎上，提出了一種基于激光跟蹤儀的機器人標定的方法，即直接標定法。運用微分變換方法建立了六自由度模塊化機器人誤差模型，并對建立的誤差模型進行驗證。利用激光跟蹤儀直接測量機器人位姿進行標定試驗，確定機器人末端位姿與運動學參數誤差的關系，把得到的機器人運動學幾何參數偏差補償到控制系統軟件中，對其中的運動學方程加以修正，然后對機器人進行二次標定。標定前后數據對比證明，機器人運動精度提升了50%。

激光跟蹤儀；直接標定法；誤差模型；運動學方程

機器人在制造裝配過程中容易產生一些誤差，這些誤差對機器人的運動精度會有較大的影響，所以減小誤差對提高機器人運動精度至關重要。對機器人進行標定的目的是了解末端位姿與運動學幾何參數誤差之間的準確關系。在機器人加工制造和裝配過程中會使連桿長度參數和連桿偏置參數產生誤差。相鄰直線之間的平行度和垂直度會產生連桿扭角誤差。在機器人裝配過程中，由于電動機編碼器的零點與機器人三維模型中關節的旋轉零位不在同一軸線上，會產生關節角誤差。為了提高機器人運動精度，需要通過機器人標定對這些參數進行補償[1-2]。

1 六自由度模塊化機器人運動學模型

1.1 機器人關節結構

六自由度模塊化機器人在機械系統設計過程中運用了模塊化的設計思想[3-4]。機器人由6個不同尺寸和構型的關節模塊組成，各模塊之間采用統一的接口連接， 通過增減模塊數量和更換不同功能的模塊，可快速裝配出符合工作要求的機器人。每一個模塊都可以單獨控制運動，模塊中包含旋轉運動和回轉運動2種形式，將6個模塊組合起來構成六自由度模塊化機器人，其構型與六自由度工業串聯型關節機器人類似。六自由度模塊化機器人的UG三維圖和實物圖如圖1所示。

圖1 六自由度焊接機器人外形圖

1.2 機器人運動學模型

采用D-H法構建機器人連桿坐標系，可得到4個連桿參數：連桿長度ai-1、連桿扭角αi-1、連桿距離di和關節轉角θi。機器人連桿參數見表1，機器人連桿的D-H坐標系如圖2所示。

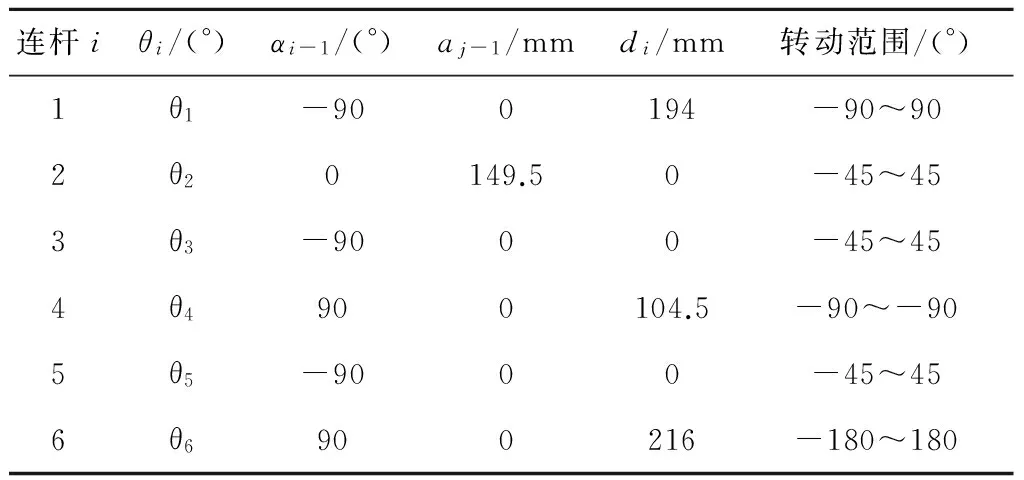
表1 機器人連桿參數表

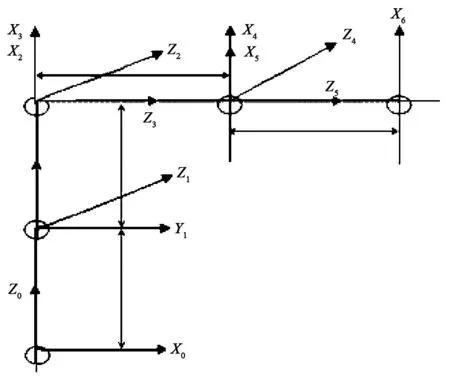
圖2 機器人連桿D-H坐標系

1.3 機器人運動學分析

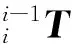
(1)

式中，cθi為cosθi；sθi為sinθi;cαi為cosαi;sαi為sinαi。

同理可知，第i個坐標系的表達式為：

(2)

由表1和式2可得：

(3)

(4)

(5)

(6)

(7)

(8)

式中，Ci為cosθi；Si為sinθi。

將6個連桿矩陣連乘，可得：

(9)

方程中的px、py、pz分別代表機器人的末端位置坐標，由于方程計算量較大，所以借助MATLAB軟件對機器人運動學方程進行求解。

2 六自由度模塊化機器人運動學標定

建立機器人運動學模型的目的是找出機器人各幾何參數與機器人末端執行器位置和姿態之間的函數關系式，其中必然包含機器人的幾何結構參數。在運動學模型的求解中，因為是理論研究，所以沒有考慮誤差；但是，在實際操作和加工過程中是存在誤差的，機器人運動學標定就是利用某種算法標識出機器人運動學參數誤差，并對其進行修正[5]。

2.1 建立誤差模型

本文采用微分變換思想對機器人誤差進行建模。

由上述機器人各關節變換矩陣連乘可得出其末端位姿。設：

P=F(a,d,α,θ)

(10)

則實際制造裝配完成的機器人末端位姿為：

P′=F(a+Δa,d+Δd,α+Δα,θ+Δθ)

(11)

進而得到機器人實際與理論位姿的誤差為：

ΔP=P-P′

(12)

因為得到的誤差數值較小，所以可以將得到的誤差進行簡化，從而得到相應的線性方程。簡化后得到的結果為：

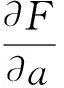
(13)

對于六自由度模塊化機器人，式13中?a表示?a0、?a1、?a2、?a3、?a4、?a5；?α表示?α0、?α1、?α2、?α3、?α4、?α5；?d表示?d1、?d2、?d3、?d4、?d5、?d6；?θ表示?θ1、?θ2、?θ3、?θ4、?θ5、?θ6。

將式13用矩陣表達為：

ΔP=JδΔδ=P-P′

(14)

(15)

則誤差系數矩陣可表達為：

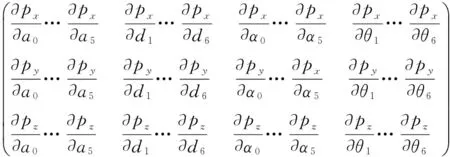
(16)

2.2 標定試驗

本文的標定試驗采用直接標定法對六自由度模塊化機器人進行標定。直接標定法就是應用高精度測量儀器測得機器人末端坐標，將坐標代入到誤差模型中求得機器人幾何參數誤差，從而建立起機器人末端坐標與運動學參數誤差的函數關系，把得到的Jδ幾何參數誤差補償到控制系統軟件中[6]。

試驗中應用的是美國FARO公司制造的Xi型激光跟蹤儀(見圖3)，這種激光跟蹤儀的測量精度比六自由度模塊化機器人精度高很多，可以保證標定試驗的準確性[7-8]。

調制比m=1時,從直流電壓利用率方面分析,采用SVPWM調制方式比SPWM調制模式提高15%以上[13]。

圖3 美國FARO激光跟蹤儀

利用激光跟蹤儀測量的數據包括三部分：機器人基坐標系的測量、機器人基本參數的測量和機器人實際位置的測量。機器人基坐標系測量是為了在激光跟蹤儀內建立機器人的坐標系；機器人基本參數測量主要是為了得到機器人的運動學幾何參數誤差；通過機器人實際位置的測量可確定機器人實際位置與理論位置的偏差。

通過上述測量的數據可以驗證誤差模型的正確性。將測量得到的運動學幾何參數誤差代入到誤差模型中，可得到機器人理論的位置誤差，將理論位置誤差與測量得到的位置誤差進行對比(見表2)，可以看出，偏差在合理范圍之內，證明了誤差模型的正確性。將測量得到的位置誤差代入到誤差模型，可得到理論的運動學幾何參數誤差，將其與測量得到的實際運動學幾何參數誤差對比(見表3)，可進一步證明誤差模型的正確性。

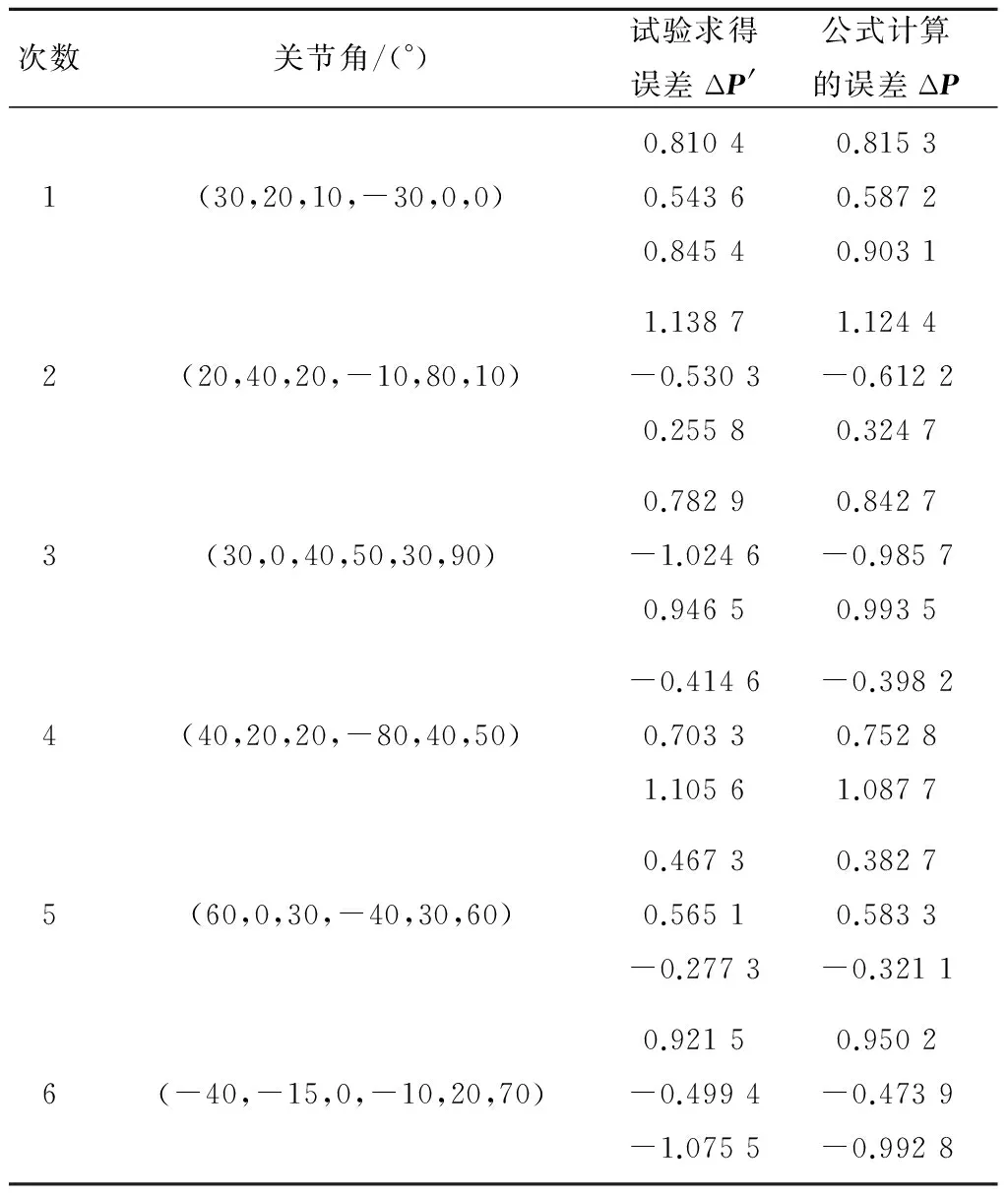
表2 實際誤差與理論誤差數據對比

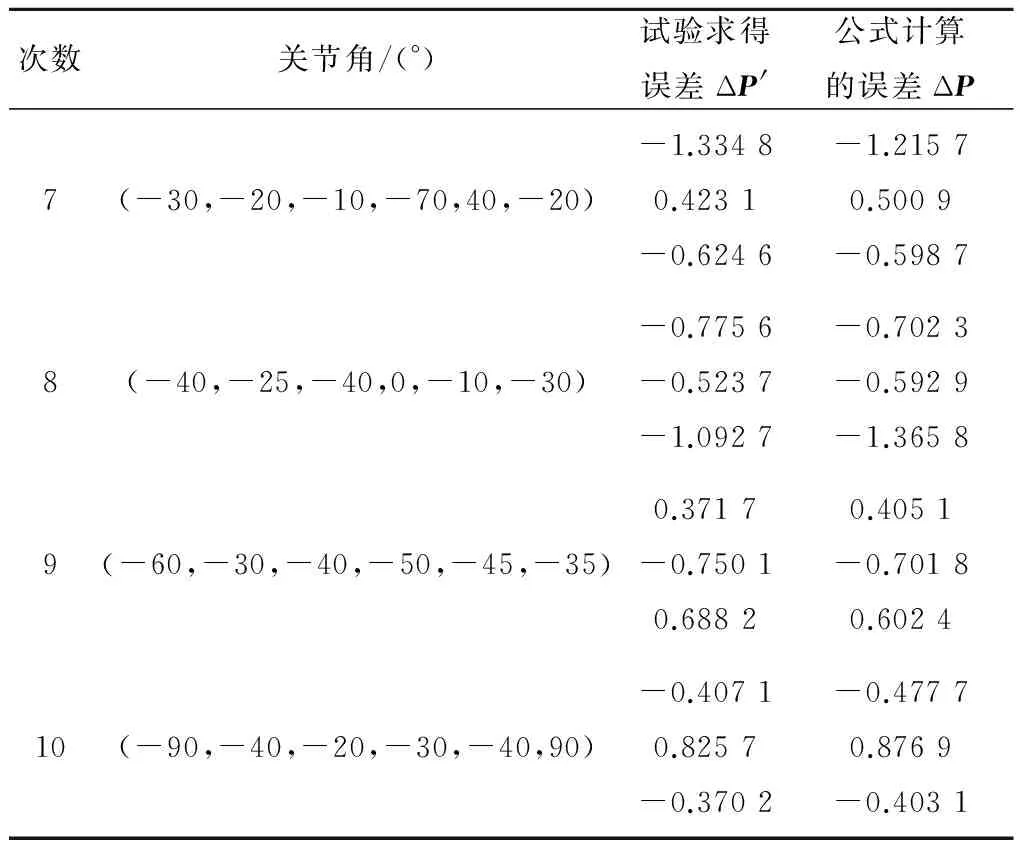
續表

2.3 誤差補償

將得到的機器人運動學幾何參數偏差補償到控制系統軟件中的運動學方程，然后運用同樣的方法測量機器人末端位置的基坐標，得到補償后的機器人誤差(見表4)，將其與補償前的數據(見表5)進行對比。

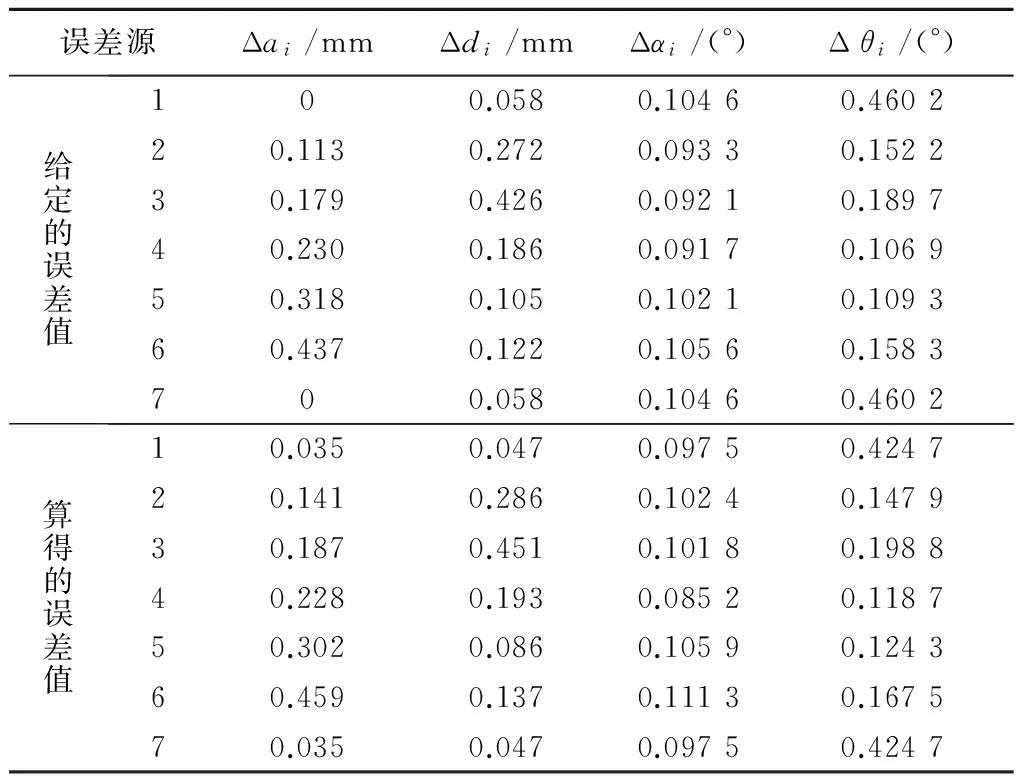
表3 測量幾何參數與理論幾何參數數據對比

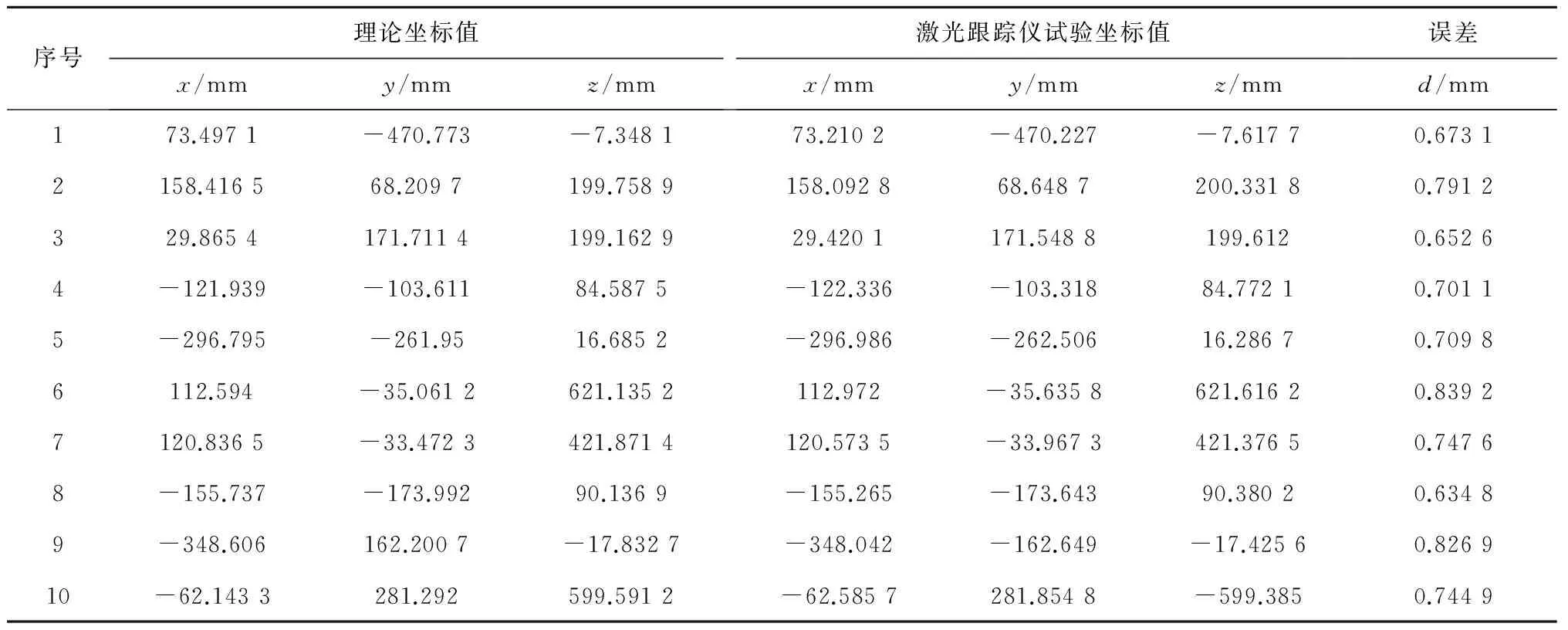
表4 補償后機器人誤差

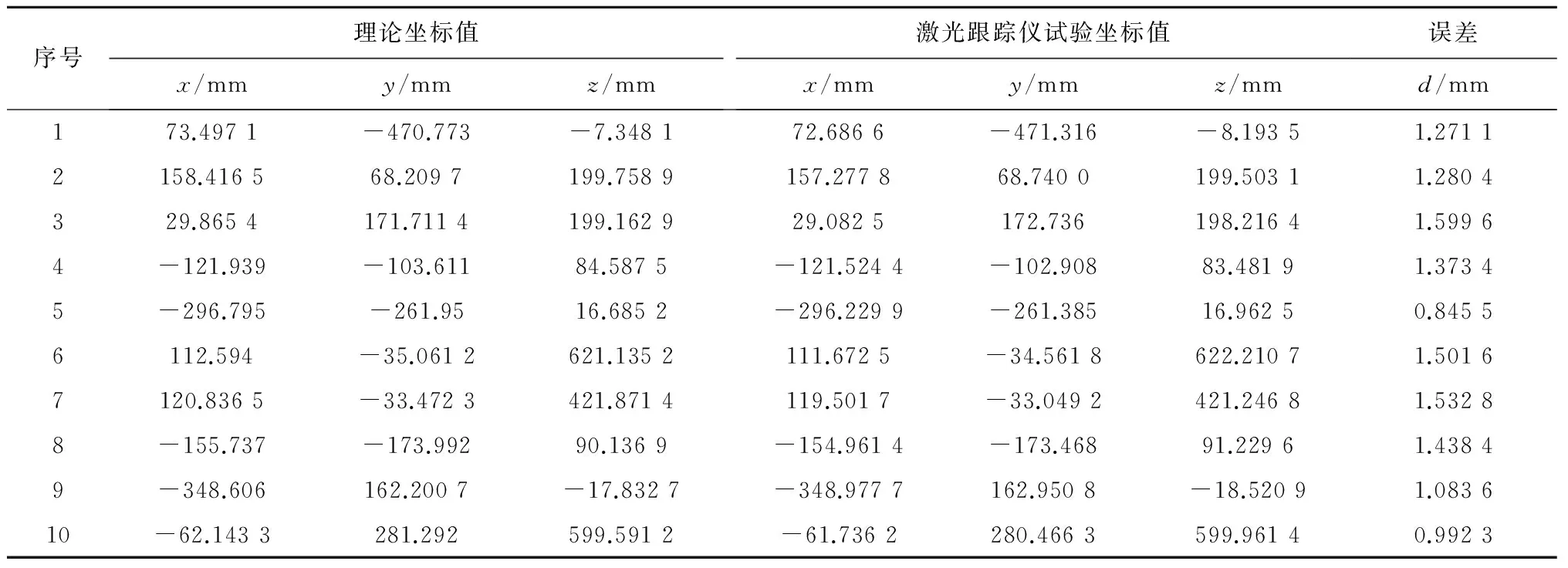
表5 補償前機器人誤差

觀察表4可知，經過補償后的機器人的末端位置坐標值與理論坐標值的偏差減小，說明機器人的運動精度有所提高，證明誤差補償具有意義；對比表4和表5的誤差數據可知，將補償后標定試驗得到的誤差數值與標定前的誤差值相比，機器人末端位置誤差值減小了50%，達到了標定試驗的預期目標。

3 結語

1)運用激光跟蹤儀對機器人進行運動學標定試驗，通過試驗測得的數據對已建立的誤差模型和試驗方案的可行性、合理性進行了驗證，證明了用微分變換的方法推導出機器人誤差模型是正確的。

2)通過對機器人控制系統中的運動學參數進行補償，機器人的運動精度提高了50%。

[1] 葉聲華，王一，任永杰，等. 基于激光跟蹤儀的機器人運動學參數標定方法[J]. 天津大學學報，2007(2)：202-205.

[2] 趙偉.基于激光跟蹤儀測量的機器人定位精度提高技術研究[D].浙江：浙江大學，2013.

[3] 王永甲.可重構模塊化機器人構型設計理論與運動學研究[D].南京：南京理工大學，2008.

[4] 王衛忠.可重構模塊化機器人系統關鍵技術研究[D].哈爾濱：哈爾濱工業大學，2007.

[5] 王品, 廖啟征, 莊育鋒, 等．一般7R串聯機器人標定的仿真與實驗[J].機器人,2006, 28(5):483-487.

[6] 龔星如，沈建新，田威，等.工業機器人定位誤差補償方法與實驗研究[J].機械與電子，2011，19(7)：64-67.

[7] 張振久，胡泓，劉欣.基于激光跟蹤儀的機床導軌系統誤差檢測[J].中國激光，2012，38(9)：159-164.

[8] 齊立哲，陳磊，王偉余，等.基于激光跟蹤儀的機器人誤差測量系統標定[J].制造技術與機床，2012(10)：90-94.

*國家“八六三”高技術項目(2012AA041402)北京石油化工學院大學生研究訓練(URT)計劃項目(2014J00118)

責任編輯鄭練

KinematicsCalibrationSixDegreesofFreedomModularRobotbasedonLaserTracker

WANG Yanmeng1, SHI Chengjiang1, WANG Dianjun2, LIU Shujing2, LI Qiang2, ZHANG Yiwan1

(1.Mechanical Engineering Academy, Liaoning Shihua University, Fushun 113001, China;2.Mechanical Engineering Academy, Beijng Institute of Petro-chemical Technology, Beijing 102617, China)

On the basis of the full research on domestic and overseas calibration methods of robots, a robot calibration method based on laser tracker is proposed, and it is named the direct calibration method. Use differential transform method to establish six degrees of freedom of the modular robot error model, and verify the error model. Use laser tracker directly measure the position and posture to do robot calibration experiment, determine the relationship of the position and posture of the end of the robot and the error of kinematics parameter. Put the error of robot kinematics geometry parameters into the control system software to compensate the original values, on which the kinematics equation is modified. Then we calibrate the robot in the second time. The contrast of data before and after calibrating proves that the robot motion accuracy has increased by 50%.

laser tracker, direct calibration method, error model, kinematics equation

TP 242.6

:A

王艷孟(1987-)，男，碩士研究生，主要從事機電一體化和機器人技術等方面的研究。

王殿君

2014-11-27