單驅單向AGV機器人運動學分析及仿真*
劉欠洋,王殿君,劉占民,陳康偉,嵇鐘輝,魏 輝
(1.北京工業大學 機電學院,北京 100124;2.北京石油化工學院 機械工程學院,北京 102617)
單驅單向AGV機器人運動學分析及仿真*
劉欠洋1,王殿君2,劉占民2,陳康偉2,嵇鐘輝2,魏 輝2
(1.北京工業大學 機電學院,北京 100124;2.北京石油化工學院 機械工程學院,北京 102617)
隨著AGV機器人的廣泛發展和應用,實際工況中AGV機器人工作空間軌跡規劃問題日趨突出,AGV機器人的運動學分析變得日益重要。基于單驅單向AGV機器人的構型特點,運用車輪差速轉彎原理和ADAMS仿真,對單驅單向AGV機器人分別進行了運動學分析及仿真。通過對比機器人理論分析和仿真的最小轉彎半徑的偏差,驗證了運動學理論分析和ADAMS仿真的正確性及合理性。在AGV機器人的理論研究、結構設計和工作空間軌跡規劃等方面有重要參考價值。
AGV機器人;運動學分析;ADAMS仿真;轉彎半徑
隨著現代制造業自動化程度不斷地向前推進,物料運輸的自動化改造也越來越受到重視。自動導航運輸車[1-3](Automated Guided Vehicle,AGV)在物料運輸領域中的應用,不僅將人工解放出來,而且由于AGV機器人運行穩定、性能可靠、投入成本低以及不會疲勞等特點,大大提高了企業的生產效率。AGV的能源為蓄電池,通過非接觸的制導方式引導機器人按照預定的路線運動。在保證AGV機器人正常工作的前提下,應盡量節省機器人工作時所占用空間。AGV機器人的運動控制、磁條鋪設、工作空間軌跡規劃和性能分析,需要以AGV機器人的運動學分析作為其理論依據[4-5]。
本文首先介紹單驅單向AGV機器人(下述簡稱AGV機器人)的機械結構,運用車輪差速轉彎原理建立方程,得出AGV機器人運動學模型公式,并求得AGV機器人最小轉彎半徑[6-8];然后,應用ADAMS軟件對AGV機器人進行仿真,提取仿真中AGV機器人的最小轉彎半徑;最后,比較AGV機器人最小轉彎半徑的理論值和仿真值,以驗證運動分析和仿真的準確性。
1 AGV機器人運動學模型的構建
1.1 AGV機器人結構
AGV機器人的機械結構是由外車身、車架、驅動模塊和車頭四部分組成。驅動模塊位于車架中部,AGV機器人的移動和轉彎主要通過驅動模塊來實現。在控制系統軟硬件和磁條導引的控制下,AGV機器人可以按照預設的軌跡路線進行作業,實現在不同復雜工況下的預設行走任務。AGV機器人三維模型如圖1所示,AGV機器人驅動模塊位置如圖2所示。
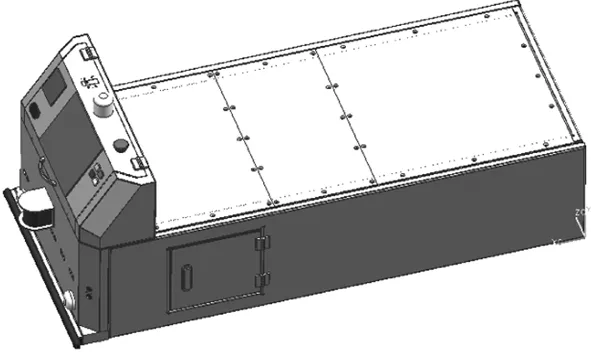
圖1 AGV機器人三維模型
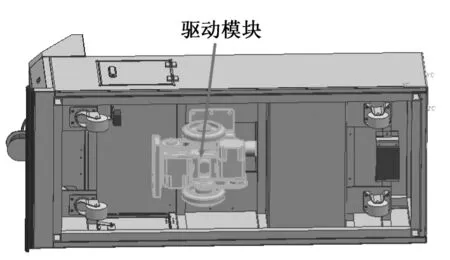
圖2 AGV機器人驅動模塊位置
1.2 AGV機器人運動學模型
在對AGV機器人的機械本體進行簡化時,考慮到AGV機器人的轉彎半徑通常相對于車體較大,并且其運行速度通常≤50 m/min,所以可以將AGV機器人的輪系與地面的側滑現象忽略。在假設AGV機器人的運動平面為水平面以及忽略其輪系與地面的打滑現象的條件下,AGV機器人在二維水平面世界坐標系的運動狀態如圖3所示。
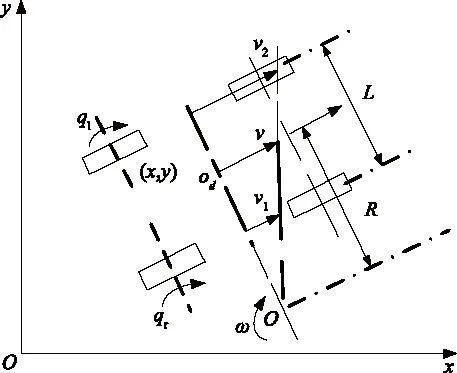
圖3 AGV機器人轉向示意圖
將圖3中世界水平坐標系用O-xy表示,而固定在AGV機器人的移動坐標系用Od-xdyd表示,Od為固定在AGV機器人上的移動坐標系的坐標原點,其與AGV機器人的幾何中心重合[9-10]。本文所研究的AGV機器人中只含有1個驅動模塊,而驅動模塊中包含左、右2個驅動輪以及其他裝置。
圖3中,ql和qr分別表示驅動模塊中的左驅動輪和右驅動輪角速度;R表示自動導航機器人的轉彎半徑;ω表示AGV機器人本體轉彎時的轉動的角速度;L表示AGV機器人的驅動模塊中左、右驅動輪中心距;v2表示驅動模塊左驅動輪的線速度;v1表示驅動模塊右驅動輪的線速度;v表示AGV機器人的幾何中心Od的速度,其表達式為:
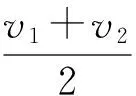
(1)
機器人本體轉彎時的轉動的角速度ω的表達式為:
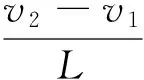
(2)
根據式2可以推導出機器人的轉彎半徑R的數學表達式為:
(3)
AGV機器人位移示意圖如圖4所示。AGV機器人運動到A點,其幾何中心與A點重合,左、右驅動輪分別在B點和C點,AGV機器人繼續行走,行走的時間為t,此時AGV機器人轉過θ1的角度。其幾何中心到達A1,此時左、右驅動輪分別在B1點和C1點位置。
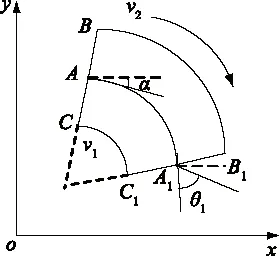
圖4 AGV機器人位移示意圖
在圖4中,當AGV機器人由A點向B點運動時,其左驅動輪運動距離大于右驅動輪運動距離。左、右驅動輪的位移差S可表示為式4或式5:
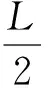
(4)
S=qlrt-qrrt
(5)
式中,r是驅動輪的半徑。
聯立式4和式5,可以得出:
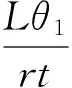
(6)
由式6可以看出,如果AGV機器人做直線運動,那么此時θ1=0,進而可以得出ql=qr,即左、右驅動輪等速運轉。
因為驅動模塊左、右驅動輪之間的距離不變,由此可以得出輪距L的計算公式如下:
(xl-xr)2+(yl-yr)2=L2
(7)
AGV機器人的前進方向與x軸的夾角和AGV機器人的左、右驅動輪中心的坐標關系表達式為:
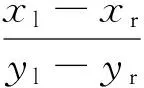
(8)
聯立式7和式8,可得出:
xl-xr=Lsin(α+θ1)
(9)
yl-yr=Lcos(α+θ1)
(10)
由圖4可以得出,AGV機器人的幾何中心坐標與AGV機器人的幾何中心的速度v和角速度的函數關系式為:
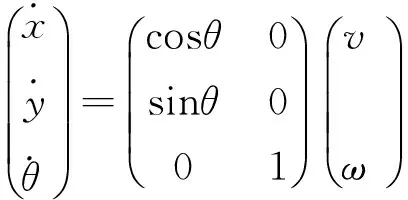
(11)
式中,θ是AGV機器人車頭與x軸的轉角,θ=α+θ1;α是AGV機器人初始狀態時的轉向角。
左、右驅動輪的速度與角速度的關系如下:
(12)
根據式1、式2和式12,可得出AGV機器人幾何中心速度v和角速度ω與左、右驅動輪的數學表達式:
(13)
根據D-H建模規則,聯立式11和式13,得出如下表達式:
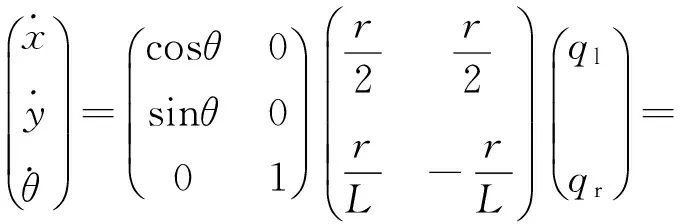
(14)
對式14中的x、y、θ分別積分,得到如下表達式:
(15)
式15即為AGV機器人的運動學模型。
1.3 AGV機器人的最小轉彎半徑
式3可變形為:
(16)
由于AGV機器人只能前進,不能后退,所以v1、v2均>0。假設v2≥v1,AGV機器人向右側轉彎,令X=v1/v2,且X∈[0,1],則式16可簡化為:
(17)
進一步化簡式17,可得:
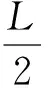
(18)
由式18可知,R是關于X的單調遞增函數。當X=0時,R最小為L/2;當X=1時,R為無窮大,即AGV機器人沿直線行駛。
本文令L=237.05 mm,所以轉彎半徑最小為118.5 mm。應用MATLAB軟件繪制的轉彎半徑R與左、右驅動輪速度比值X的關系圖如圖5所示。
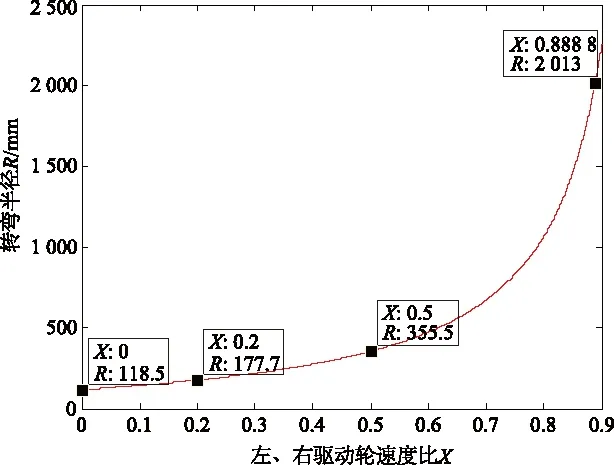
圖5 轉彎半徑R與左、右驅動輪速度比值X的關系圖
圖5中取了4個點,分別是:當X=0.888 8時,R=2 013 mm;當X=0.5時,R=355.5 mm;當X=0.2時,R=177.7 mm;當X=0時,R=118.5 mm。通過圖5可以看出,當X=0時,轉彎半徑最小,即當v1=0(右驅動輪線速度為零)時,AGV機器人向右側轉彎半徑最小(值為118.5 mm)。
2 AGV機器人的仿真
2.1 虛擬樣機的建立
基于AGV機器人的三維模型以及ADAMS軟件中AGV機器人的虛擬樣機,對所研究的AGV機器人進行仿真。導入ADAMS后的效果如圖6所示。

圖6 ADAMS中的AGV機器人虛擬樣機效果圖
在ADAMS軟件中建立虛擬樣機后,首先將不需要進行仿真的AGV機器人的部件利用固定副進行連接,使其不能發生相對運動;其次,對支承輪和驅動輪創建旋轉副;然后,對剩余部件使用對應運動副進行連接;最后,在地面和各個車輪之間創建接觸。
將虛擬樣機中的各個部分連接好后,在左、右驅動輪上添加驅動。由于驅動模塊上有一個彈簧給驅動模塊提供正壓力,所以還需要在驅動模塊和車架之間添加彈簧,將彈簧系數設置為15 N·mm,并添加預緊力。
2.2 機器人運動學仿真與分析
本文所進行的仿真過程是,控制左驅動輪不轉,控制右驅動輪進行運動。這樣虛擬樣機就會在地面上進行轉彎。右驅動輪的驅動方程如下:
step(time,0,0d,2,0d)+step(time,2,0d,2.5,-509.29d)+step(time,2.5,0d,4.5,0d)+step(time,4.5,0d,5,509.29d)
仿真完成后,將左、右驅動模塊的中心點的運動軌跡投射到地面上,并在地面上顯示出來。AGV機器人虛擬樣機的運動軌跡如圖7所示。
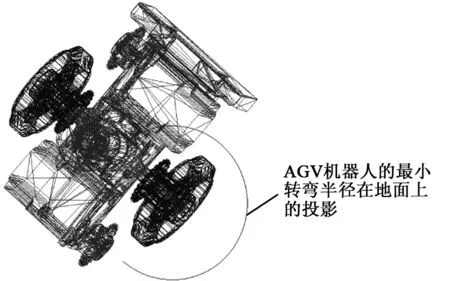
圖7 AGV機器人的運動軌跡
從ADAMS軟件中將軌跡點坐標信息提取,然后將軌跡點坐標信息導入MATLAB軟件中。在MATLAB軟件中,利用軌跡點坐標信息將軌跡點擬合成圓,計算擬合圓的圓心坐標X1、Y1以及半徑R。最后求解出R≈118.8 mm,即通過ADAMS軟件對本文所研究的AGV機器人進行運動學仿真,求解出AGV機器人的最小轉彎半徑為118.8 mm。
3 對比
通過理論分析,利用運動學方程求解出最小轉彎半徑為118.5 mm;基于ADAMS軟件對機器人進行運動學仿真,得出的最小轉彎半徑為118.8 mm。顯而易見,通過2種方式求解出來的AGV機器人的最小轉彎半徑偏差為0.3 mm,可以忽略。這也說明了本文AGV機器人的理論分析和運動學仿真方法的正確性。
4 結語
1)對AGV機器人進行了運動學分析,利用車輪差速轉彎原理建立了運動學模型,得出了AGV機器人的運動學方程,并求得了AGV機器人的最小轉彎半徑。
2)基于ADAMS軟件,對AGV機器人進行了運動學仿真,并根據AGV機器人轉彎時的軌跡坐標,求得了運動學仿真中AGV機器人的最小轉彎半徑。
3)將AGV機器人最小轉彎半徑的理論數據和仿真數據進行對比,其最大偏差為0.3 mm,偏差在合理范圍內,說明本文所進行的運動學理論分析和仿真方法的正確性。
4)本文所研究的AGV機器人的最小轉彎半徑為118.8 mm,對AGV機器人在結構設計、工作空間軌跡規劃和通過性能分析等方面有重要參考價值。
[1] 趙鶴君. 國外AGV的發展、應用與展望[J]. 鐵道物資科學管理, 1993, 11(3): 8-9.
[2] 唐文偉. AGV在物流領域中的應用前景分析[J]. 物流技術, 2001, 108(3):7-8.
[3] 李季. 磁導引AGV的設計[D]. 濟南: 山東大學, 2013.
[4] 倪振. 激光導引四輪差動全方位移動AGV關鍵技術研究[D]. 重慶: 重慶大學, 2013.
[5] 周馳東. 磁導航自動導向小車(AGV)關鍵技術與應用研究[D]. 南京: 南京航空航空大學, 2012.
[6] 李進, 陳無畏, 李碧春, 等. 自動導引車視覺導航的路徑識別和跟蹤控制[J]. 農業機械學報, 2008, 39(2):20-24.
[7] 尹曉紅. 自動引導車運動分段控制技術研究[D]. 合肥: 合肥工業大學, 2011.
[8] 賀麗娜. AGV系統運行路徑優化技術研究[D]. 南京: 南京航空航天大學, 2011.
[9] 蔣新松. 機器人學導論[M]. 沈陽: 遼寧科學技術出版社, 1994.
[10] 常勇, 馬書根, 王洪光, 等. 輪式移動機器人運動學建模方法[J]. 機械工程學報, 2010, 46(5):30-36.
*北京石油化工學院大學生研究訓練(URT)計劃項目(2014J00087)
責任編輯鄭練
TheKinematicsAnalysisandSimulationofSingle-driveandSingle-directionAGVRobot
LIU Qianyang1, WANG Dianjun2, LIU Zhanmin2, CHEN Kangwei2, JI Zhonghui2, WEI Hui2
(1.Beijing University of Technology, Beijing 100124, China;2.Beijing Institute of Petrochemical Technology, Beijing 102617, China)
With the extensive development and application of AGV (Automated Guided Vehicle) robots. In practice, AGV robots working space trajectory planning problems have become more prominent. The kinematics analysis of AGV robot is becoming increasingly important. Based on single-drive and single-direction AGV robot configuration features,using wheel differential turning principle and ADAMS analyzes and simulates kinematics of single-drive and single-direction AGV robot respectively. The deviation between the theory analysis and simulation of minimum turning radius of the robot is very small, and it verifies that the correctness and rationality of the kinematics theory analysis and ADAMS simulation. This paper has important reference value in the theory study, structure design and working space trajectory planning of AGV robot.
AGV robot, kinematics analysis, ADAMS simulation, turning radius
TP 242.2
:A
劉欠洋(1989-),男,碩士研究生,主要從事機器人技術等方面的研究。
王殿君
2014-11-27

