基于相關向量機的加速度計參數變化規律研究

楊繼紅，于湘濤，付秀娟，于 皓，韓 旭，龔錦莉

（1.海軍駐某院軍事代表室，北京 100074;2.北京自動化控制設備研究所，北京 100074）

在已知超先驗情況下，對p（t|α，σ2）取最大值

0 引言

慣性導航是一門涉及多學科的綜合性技術，是實現運動體自主式控制和測量的最佳途徑，廣泛應用于航天、航空、航海等領域［1］，石英撓性加速度計 （以下簡稱加速度計）作為慣性導航系統最重要的器件之一，其測量精度高低直接影響慣性系統的精度［2］。加速度計受溫度等環境載荷以及其內部構件材料的特性的影響，加速度計參數隨時間會發生漂移，從而導致加速度計的輸出發生變化［3］，因此，進行加速度計參數變化規律的研究對于提高慣性導航系統的精度具有重要意義。

相關 向 量機［4］（Relevance Vector Machine，RVM）是 Tipping提出的一種與支持向量機［5］（Support Vector Machine，SVM）形式相同的稀疏概率模型，其訓練是在貝葉斯框架下進行的，通過超參數給出權值的先驗概率，并通過迭代算法求出最優值，在實際預測性能相當的情況下，解的稀疏性明顯高于SVM。

基于RVM的優點，建立了加速度計參數RVM預測模型，為了驗證所提方法的有效性，針對2.5年自然貯存的加速度計參數標定值，應用RVM和最小二乘法分別進行了加速度計參數建模，計算結果表明RVM建模效果更優。

1 模型預測算法

時間序列預測［6］是指利用歷史數據構建時間序列模型，依據所建模型進行外推預測未來。統計學方法是時間序列預測的主要方法，常見的時間序列分析方法包括:自回歸滑動平均模型 （Autoregressive Moving Average，ARMA）等，基于機器學習理論發展起來的人工神經網絡和支持向量算法等智能預測方法具有自適應、自學習機制，可以對非線性時間序列進行更準確地預測。

1.1 ARMA模型試驗時間預測方法

ARMA模型時間序列分析法簡稱為時序分析法，是一種利用參數模型對有序隨機數據進行處理，從而進行參數預測的方法，參數模型包括AR自回歸模型、MA滑動平均模型和ARMA自回歸滑動平均模型，ARMA時間序列具有遍歷性。

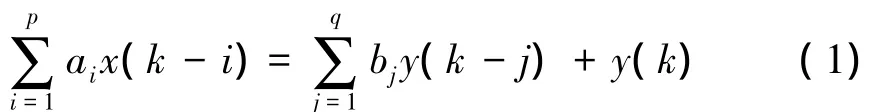
式 （1）的左邊稱為自回歸差分多項式，即AR模型，右邊稱為滑動平均差分多項式，即MA模型，p、q為自回歸模型和滑動均值模型的階次，ak、bk分別表示待識別的自回歸系數和滑動均值系數，y表示白噪聲激勵。

確定ARMA模型的階數，即p和q的數值的求解可以通過 AIC（Akaike Information Criterion，AIC）法、F檢驗法等方法求解，自回歸系數可以通過建立Yule-walker方程，采用偽逆法可求得方程組的最小二乘解，滑動平均模型MA系數的估算方法很多，主要的有基于Newton-Raphson算法的迭代最優化方法和基于最小二乘原理的次最優化方法。

1.2 相關向量機算法

相關向量機是Tipping提出的一種貝葉斯框架下的稀疏概率機器學習模型，假設一系列輸入向量 x={xn，n=1，2，．．．，N}和相應的輸出 y={yn，n=1，2，．．．，N}， 設計的模型對于新的輸入xn，預測出輸出y（xn），所觀測的輸出tn，它可以看作未知函數y（x，w），該函數包含方差為σ2的高斯噪聲。

式中，ε是噪聲信號，且是獨立分布的，w是可調參數權值，其中Φi（x）=K（x，xi），這里的核函數的選擇不受Mercer定理的限制。相應的訓練樣本集的似然函數為

采用稀疏貝葉斯方法對權值w賦予先驗的條件概率分布

式中，α是決定權值先驗分布的超參數，根據貝葉斯公式可以得到

在已知超先驗情況下，對p（t|α，σ2）取最大值

由于不能直接獲得式 （6）中α和σ的解析表達式，因此，使用迭代公式進行估計。

式中，γi=1－αiNii，Nii為后驗權協方差矩陣的第i個對角元素。

若給定一個輸入值x*，則可通過下面幾步實現新的預測。

RVM對新觀測值的預測輸出為y（x*;μ）。

2 加速度計參數變化規律

2.1 加速度計參數變化原因分析

1）膠粘劑材料穩定性:在加速度計關鍵的部組件——磁鋼與激勵環、動圈與石英擺片等位置采用膠粘劑連接，膠粘劑在長期環境載荷作用下會發生蠕變，蠕變是通過分子鏈段的逐漸伸展或相對滑移實現的，結果不僅會造成力學松弛，還會使得被粘接的構件發生相對位移，膠粘劑材料的穩定性使得敏感質量的質心和電磁力的力心變化，使得加速度計參數長期重復性發生變化。

進行了膠粘劑變化導致動圈沿著擺軸移動與力矩器電磁力之間的仿真，仿真結果如圖1所示。

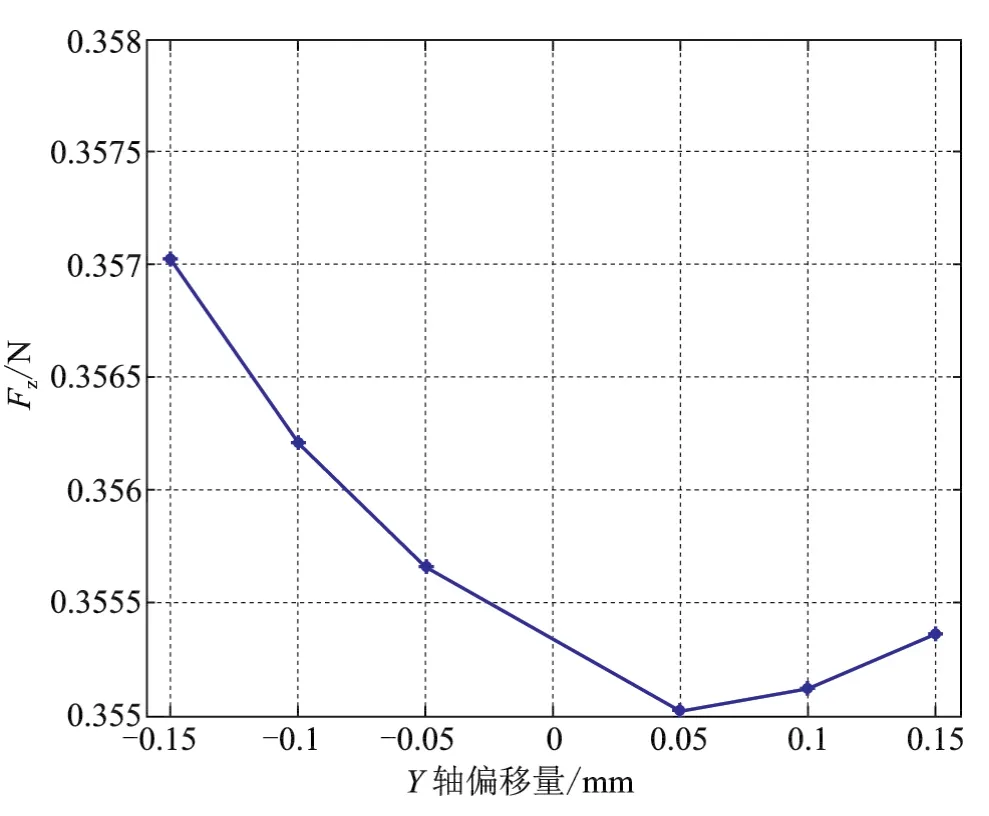
圖1 電磁力與動圈移動之間的關系示意圖Fig.1 The relationship between electro-magnetic force and the force coils movement

從圖1中可以看出線圈所受合力隨線圈沿擺軸的正負偏移量增大而增大，但是在相同偏移量的情況下，遠離撓性平橋的偏移對電磁力的影響更大。

2）永磁材料穩定性:加速度計力矩器在輸入信號作用下產生反饋力矩以平衡外界的慣性力矩，磁性能的穩定性直接影響力矩器的穩定性，磁時效是永磁材料磁性能隨時間的一種不可逆連續變化，是由于材料內部的結構調整所引起的，為了解釋磁時效現象，許多科學家進行了研究，并建立了理論模型。

進行了不同的磁鋼磁感應強度退化時的仿真，其中退化1%時，磁路云圖如圖2所示。

圖2 加速度計磁路矢量圖Fig.2 The vector graph of accelerometer magnetic circuit

仿真結果表明磁鋼退磁1%時，標度因數增大約7‰。

3）金屬構件尺寸的穩定性:材料的相與組織狀態的不穩定性及在各種熱加工與冷加工工藝過程中，零件中發生的殘余應力的松弛導致金屬制件尺寸變化，也是引起加速度計參數變化的因素之一。

2.2 加速度計長期重復性測試方案

為了評估加速度計參數變化規律，進行了加速度計長期重復性試驗設計，標定周期0.5年，總共2.5年，測試樣本18塊，將加速度計按“門狀態”安裝，如圖3所示。

“門狀態”即分度頭置于0°時，加速度計輸入基準軸 （IA）與水平面的夾角滿足技術要求，擺基準軸 （PA）平行于旋轉軸，輸出基準軸 （OA）垂直向下，當分度頭旋轉至90°時，輸入基準軸正方向垂直向上，按照GJB1037A［7］進行四點翻滾試驗標定加速度計的偏值和標度因數。

圖3 “門態”試驗安裝圖 （分度頭0°）Fig.3 The chart of the hinge axis

2.3 加速度計數據規律分析

加速度計參數RVM建模步驟:

圖4 基于最小二乘法的加速度計參數建模示意圖Fig.4 The modeling result of accelerometer based on least squares method

1）收集整理加速度計標定數據序列，Xn={x1，x2，…，xN}，xi∈ R，i=1，2，…，N;

2）對原始序列XN進行歸一化處理;

4）對樣本進行RVM預測。

應用最小二乘法和RVM建立了加速度計參數模型，模型曲線如圖4和圖5所示。

從圖4和圖5可以看出，二階回歸模型和

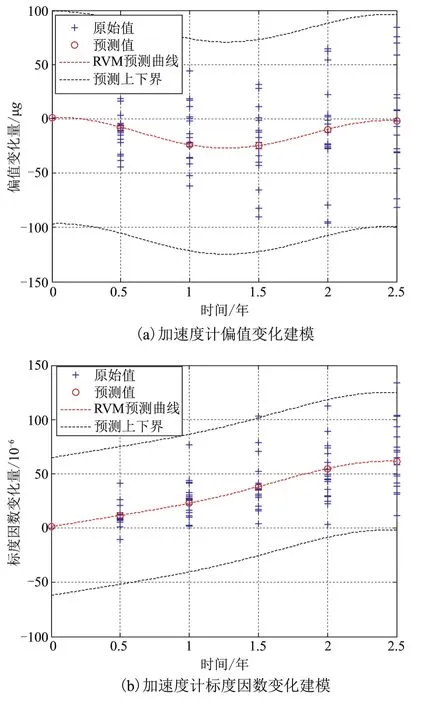
圖5 基于RVM的加速度計參數建模示意圖Fig.5 The modeling result of accelerometer based on RVM

3）選擇RVM核函數，常用的幾種核函數有RBF核函數、線性核函數、多項式核函數等。其中，RBF核函數具有較好的學習能力，選用RBF函數作為RVM的核函數，其數學表達式為RVM模型都可以用來加速度計參數變化建模，當加速度計參數變化存在非線性時，二階模型回歸與實際參數變化存在較大誤差，而RVM可以很好地給出加速度計參數變化結果。

3 結論

受溫度、振動等環境載荷的影響，加速度計參數隨著時間會發生變化，基于RVM具有稀疏的模型適合時間序列預測的優點，提出了一種加速度計參數預測方法，用RVM和最小二乘法分別建立了加速度計參數模型，計算結果表明RVM的建模效果更優。

［1］鄭辛，楊林．導航、定位與授時技術綜述［J］．導航定位與授時，2014，1（1）:1-7．

［2］顧英．慣導加速度計技術綜述［J］．飛航導彈，2001，（6）:78-85．

［3］于湘濤，張菁華，杜祖良．石英撓性加速度計參數長期重復性技術研究［J］．導航定位與授時，2014，1（1）:58-62．

［4］Tipping M E．Sparse Bayesian learning and the relevance vector machine［J］．Journal of Machine Learning Research，2001，l（3）:211-244．

［5］Vapnik V N．An overview of statistical learning theory［J］．IEEE Transactions on Neural Networks，1999，10（5）:988-1000．

［6］張美英，何杰．時間序列預測模型研究綜述［J］．數學的實踐與認識，2011，41（18）:189-195．

［7］GJB 1037A，單軸擺式伺服線加速度計試驗方法［S］．2004．