利用變步長Runge-Kutta法分析換流變壓器油紙絕緣結構瞬態電場
岳嘯鳴,范輝,李慧奇,劉剛
(1.河北省電力建設調整試驗所,河北石家莊 050021;2.華北電力大學河北省輸變電設備安全防御重點試驗室,河北保定 071003)
利用變步長Runge-Kutta法
分析換流變壓器油紙絕緣結構瞬態電場
岳嘯鳴1,范輝1,李慧奇2,劉剛2
(1.河北省電力建設調整試驗所,河北石家莊 050021;2.華北電力大學河北省輸變電設備安全防御重點試驗室,河北保定 071003)
換流變壓器極性反轉瞬態電場仿真往往采用定步長方法,為了保證計算精度,往往采用較小的時間步長,計算量較大.為了有效地降低換流變壓器極性反轉瞬態電場仿真分析時的計算代價,根據各時步的局部截斷誤差,提出采用變步長顯式Runge-Kutta法分析極性反轉瞬態電場.并用所提方法對換流變壓器閥側繞組典型模型在極性反轉電壓下的瞬態電場進行了分析,計算結果表明本文提出的方法可以有效地降低計算代價,能夠用于換流變壓器極性反轉瞬態電場的分析計算.
換流變壓器;極性反轉;瞬態電場;Runge-Kutta法;變步長
換流變壓器和絕緣套管是直流輸電工程中的重要設備,它們安全運行直接關系到系統的穩定.在直流輸電系統需要潮流反轉時,送段換流變壓器的閥側繞組電壓極性將在短時間內迅速改變,稱為極性反轉.在極性反轉過程中,換流變壓器閥側繞組端部油紙復合絕緣中會出現局部高場強,從而使換流變壓器出現絕緣故障,嚴重影響了系統的安全運行.因此研究極性反轉過程中的電場分布成為換流變壓器研制開發的關鍵[1-2].
極性反轉電場分析往往采用2種方法,即靜態法和瞬態法.采用靜態法時,假設外施電壓瞬間完成極性反轉,此時由于外加電壓的容性電場躍變,而空間電荷及其電場保持不變,因此可用阻性電場疊加兩倍負容性電場得到極性反轉的瞬間電場,這是一種理想的極端情況,但由于設備的限制,電壓極性反轉往往需要一定時間才能完成(往往需要1~2m in),因此需要考慮短時反轉過程中電荷的重新分布及其反轉完成時刻電場分布的影響.
現有文獻在用瞬態法分析極性反轉電場時,幾乎都采用定步長方式[3-8].一般說來,步長越小,截斷誤差就越小.但是,隨著步長的縮小,瞬態過程分析所需的時步數就會增加.時步數的增加,不但引起計算量和數據存儲量的增大,而且可能導致舍入誤差的嚴重積累.因此在實際計算時,需要選擇適當的步長,在滿足精度要求的前提下,盡可能地減小計算步數.一種有效的措施就是在計算過程中,根據外施激勵變化的不均勻性,在計算過程中自動地調整步長,即自適應算法.文獻[9]嘗試根據外施電壓的特點分段定義步長,這種人為設定步長的方式雖然減少了計算量,但與通常根據(截斷)誤差實現自動變步長的自適應算法明顯不同.
文獻[10]根據各時步的局部截斷誤差,采用C-N(Crank-Nilcoson)法實現自動變步長的算法,并在分析極性反轉電壓特點的基礎上,利用后向歐拉法,成功的解決了極性反轉電壓導數不連續點的時步振蕩情況,但該算法在每次極性反轉完成后的步長增長緩慢,計算的時步數較多,計算代價仍較大.
文獻[11]在分析±500 kV換流變壓器極性反轉過程時,假設極性反轉瞬間,并采用定步長四階顯式Runge-Kutta法分析了線性、非線性及非線性各向異性條件下的極性反轉電場.由于采用定步長測量,使得具有較高精度的四階Runge-Kutta法的計算效率較低.
在保證計算精度的前提下,本文根據文獻[10]的思路,即根據當前時步的截斷誤差決定下一時步的時步長,擬采用變步長顯式Runge-Kutta法采取變步長策略,以達到減少計算時步數,降低計算代價的目的.
為了簡化分析,本文暫不考慮油紙電導率同電場強度的非線性和紙板電導率各向異性的影響,給出根據局部截斷誤差得到自適應變步長的顯式Runge-Kutta法.并用變步長顯式Runge-Kutta法對換流變壓器閥側繞組典型模型的極性反轉反轉過程進行了計算,對計算結果進行了簡要分析.
1 有限元狀態方程
換流變壓器油紙絕緣結構中的瞬態電場為電準靜態場,油紙中的電位滿足如下初邊值問題[10]


表1 定步長布徹表Tab.1 Fixed time-step's Butcher table

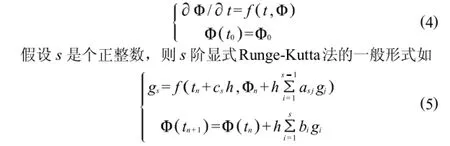
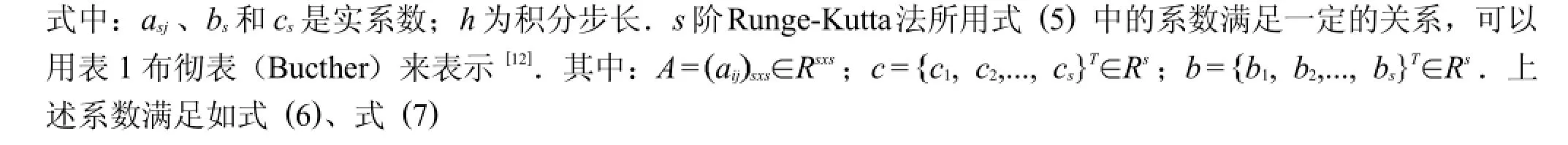

2 變步長顯式Runge-Kutta法

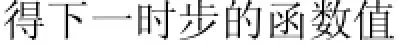
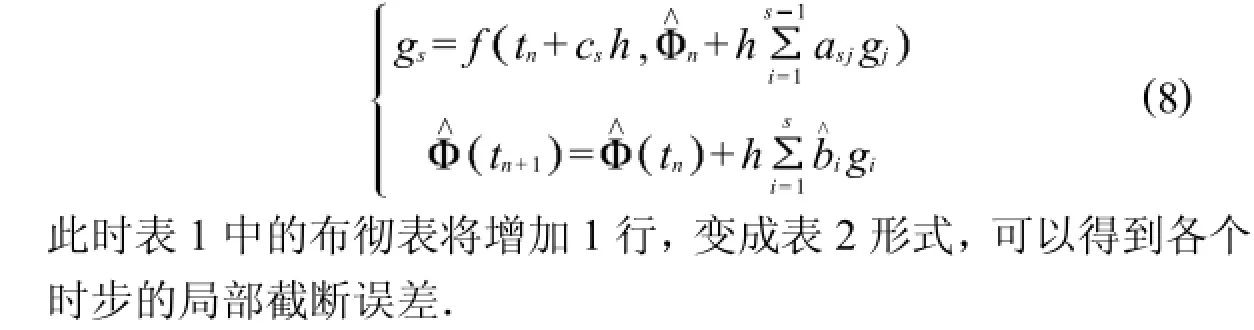

在下面的仿真分析中,采用Merson法,其相應的布徹表的參數如表3所示.

表2 變步長布徹表Tab.2 Varible time-step's Butcher table
3 極性反轉電壓
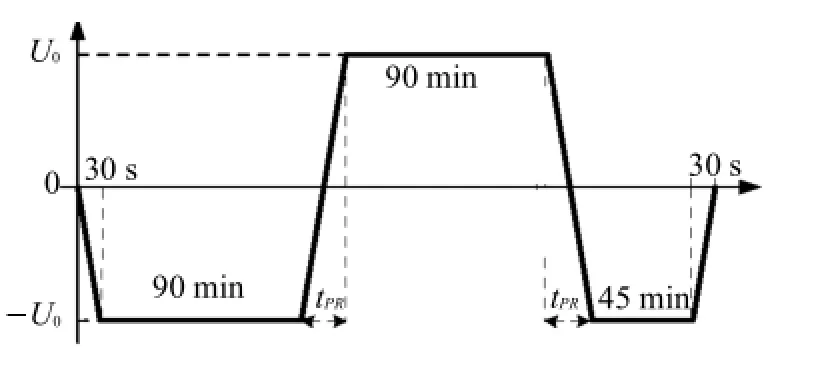
完整的極性反轉試驗需要進行2次反轉過程,電壓波形如圖1示,具體變化過程如下:1)在30 s內由0電位降到U0,保持90m in;2)在一定時間tPR內由U0上升到+U0,并保持90m in;3)在一定時間tPR內由+U0下降到U0,并保持45min;4)在30 s內均勻變化到0.
IEC推薦2次極性反轉過程不超過2m in,一般取1m in.本文計算時取為tPR=1min.
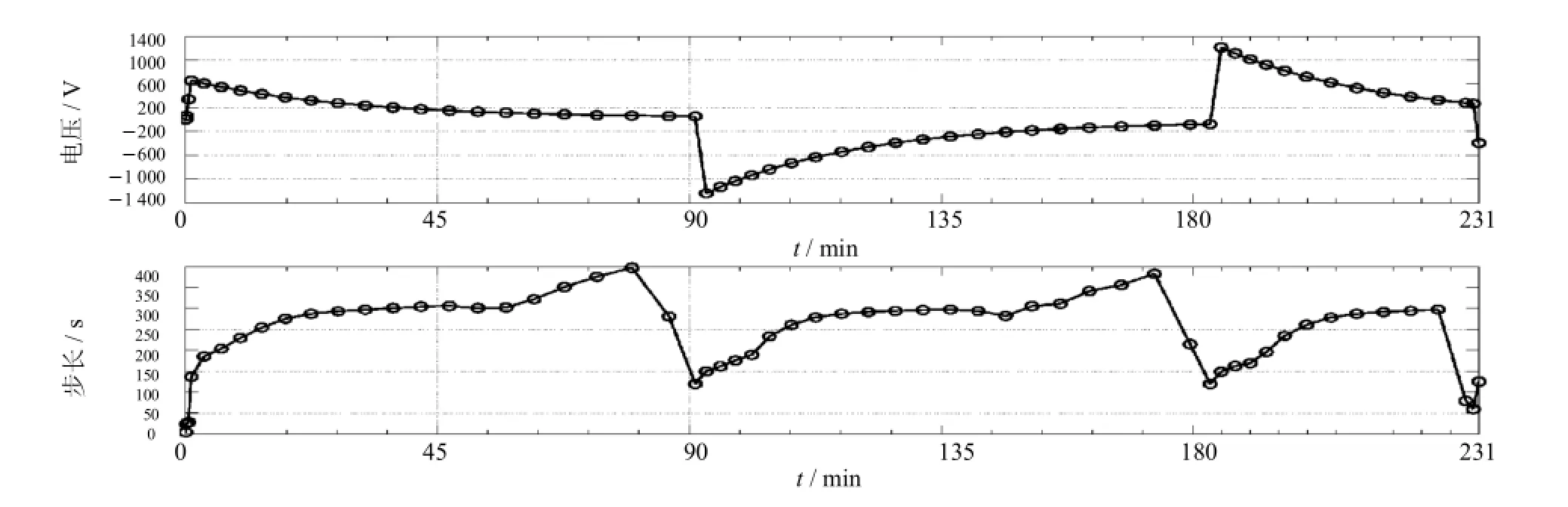
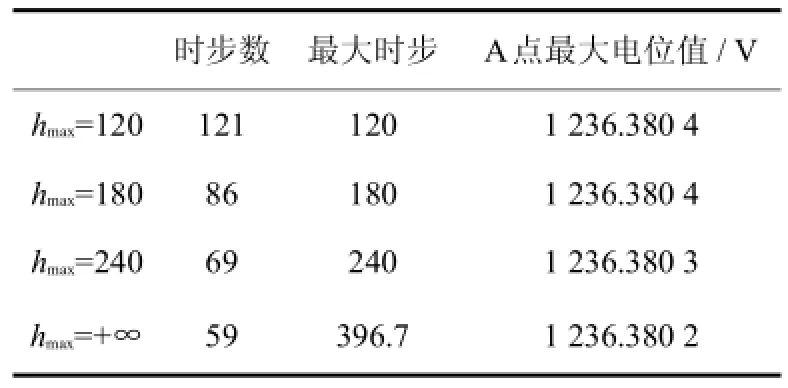
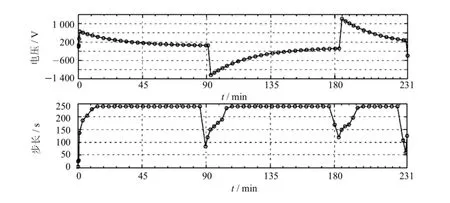
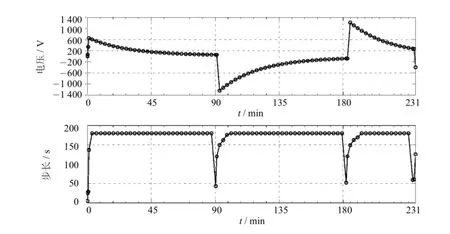
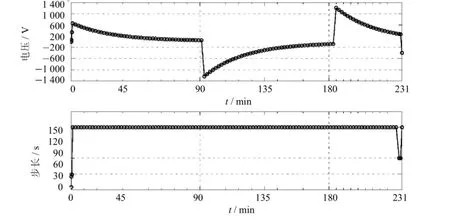
在用變步長顯式Runge-Kutta法計算圖1電壓波形下的極性反轉電場時,每個時間步計算均需要判斷當前時刻tn累加下一步長hn+1后,是否會超過極性反轉的開始時刻(tb)和完成時刻(te).假設tn 表3 Merson法的布徹表Tab.3 Merson's Butcher table 則步長hn+1保留,否則hn+1值由下式決定 這樣處理后就能保證不會因為步長過大而丟失極性反轉開始時刻tb或完成時刻te的電場信息. 圖1 極性反轉電壓波形Fig.1 PR voltage's curve 為了更好的反映極性反轉過程中的電場變化情況,往往需要知道更多時刻的電位(電場強度)值.可以給各時步的步長設定一個上限值hmax,當各下一時步hn+1的步長超過hmax時,hn+1就取hmax. 本文采用文獻[10]換流變壓器閥側繞組典型模型進行分析,為了便于本文分析,圖2重新給出了模型,圖中單位為mm. 對圖2模型采用三角形剖分,共剖分得到1 142個三角形單元,699個節點.單元電位采用線性插值,仿真分析時,極性反轉電壓幅值U0=1 000 V.采用上文變步長顯式Runge-Kutta法計算了整個極性反轉過程. 圖2 換流變壓器閥側繞組典型模型Fig.2 TypicalM odelof the converter transformer’valvew inding 本文首先只用式(13)約束下一時刻的時步hn+1,此時hmax不設上限,在此假設下整個極性反轉瞬態過程只需要59個時步,這遠遠小于定步長算法(步長為30 s時需456個時間步),計算量也遠小于文獻[10]的修正變步長C-N法.極性反轉過程中A點(圖2所示)電位和各時間步步長hn+1隨時間的變化曲線如圖3所示. 圖3 hmax=∞時的計算結果及各時步的步長Fig.3 Computational resultsand time-step ofeach time instantat hmax=∞ 結合圖1和圖3可以看出,當外施電壓保持恒定時,時步長總體上趨于增加,理論上在各次反轉開始時刻應該達到最大值.但圖3表明,反轉開始時刻的步長迅速減小,這是由于此時步長不是由此時刻的階段誤差決定,而是由式(14),式(15)決定. 由圖3可以看出,整個極性反轉過程中各時步的最大步長接近400 s.為了更好的反應極性反轉過程中的電場變化情況,往往需要知道更多時刻的電位(電場強度)值.本文在hmax取不同值時重新分析了上述極性反轉過程,并將計算結果列于表3中,同時在圖4~6中給出了A點的電位和時步同時間的變化曲線. 從表3可知,當限制hmax時,整個極性反轉過程的計算量將有所增加,但表3中的A點最大電位值卻相差很小,最大差值僅為0.000 2 V. 從上文分析可看出,即使限制了hmax值,例如hmax=120 s的時步數為121,而采用當定步長Runge-Kutta法(或C-N法)的步長取20 s、30 s和60 s時,其極性反轉瞬態過程分別需要計算684、256和228個時步,限制后的計算量仍將比定步長算法小.對于相同的極性反轉瞬態過程,文獻[8]雖然采用修正變步長法,但整個瞬態過程仍需要394個時步,而文獻[9]根據極性反轉電壓的變化認為設定時步長的方法計算量更大,因此本文的自適應變步長顯式Runge-Kutta方法可以用來快速分析換流變壓器極性反轉瞬態電場問題. 表3 hmax取不同值時的計算結果Tab.3 Computational results of different hmax 圖4 hmax=240 s時的計算結果及各時步的步長Fig.4 Computational resultsand time-stepsof each time instantat hmax=240 s 圖5 hmax=180 s時的計算結果及各時步的步長Fig.5 Computational resultsand time-stepsof each time instantat hmax=180 s 圖6 hmax=120 s時的計算結果及各時步的步長Fig.6 Computational resultsand time-steps of each time instantat hmax=120 s 本文針對換流變壓器極性反轉外施電壓的特點,提出了基于顯式Runge-Kutta法根據局部截斷誤差實現自適應變步長的算法,并將算法應用到換流變壓器極性反轉電場分析中,實際換流變壓器閥側繞組典型模型計算結果表明,采用自適應變步長顯式Runge-Kutta算法后,可以大大減少計算時步數,從而能夠降低計算量和內存需求. [1]趙婉君.高壓直流輸電工程技術[M].北京:中國電力出版社,2004. [2]宓傳龍.超高壓換流變壓器和平波電抗器絕緣結構簡述[J].高壓電器,2003,25(1):7-15. [3]文闿成.復合介質、中暫態電場的數值解[J].高電壓技術,1989,15(4):2-7. [4]Wen K C,Zhou YB,Fu J,etal.A calculationmethod and some featuresof transient field underpolarity reversalvoltage in HVDC insulation[J].IEEE Transactions on PowerDelivery,1993,8(1):223-230. [5]張艷麗,謝德馨.換流變壓器內部暫態電場分析[J].沈陽工業大學學報,2001,23(6):467-470. [6]李巖,李曉輝,唐聰,等.換流變壓器閥側繞組端部瞬態電場分析[J].高電壓技術,2012,38(11):2797-2804. [7]劉剛,李琳,李文平,等.換流變壓器極性反轉非線性電場分析[J].高電壓技術,2012,38(2):451-456. [8]劉剛,李琳,紀鋒,等.基于節點電荷電位有限元法的油紙絕緣結構極性反轉電場分析[J].中國電機工程學報,2011,31(25):132-138. [9]王冰,王清璞,孫優良.換流變壓器閥側繞組端部極性反轉瞬態電場的計算與分析[J].變壓器,2007,44(6):11-15,22. [10]劉剛,李琳,紀鋒.利用自適應時間步長有限元法計算換流變壓器油紙絕緣結構瞬態電場[J].華北電力大學學報(自然科學版),2011,38(1):17-20,106. [11]李琳,紀鋒,李文平,等.換流變壓器極性反轉試驗的數值模擬[J].中國電機工程學報,2011,31(18):107-112. [12]HairerE,NorsettSP,WannerG.Solving ordinary differentialequations I[M].北京:科學出版社,2006. [責任編輯 代俊秋] Variable runge-kuttaalgorithm for the computationof transientelectric field in oil-paper insulation construction of HVDC transformer YUEXiaom ing1,FAN Hui1,LIHuiqi2,LIU Gang2 (1.HebeiElectric PowerCommissioning Institute,Hebei Shijiazhuang 050021,China;2.HebeiProvincialKey Laboratory of Power Transmission EquipmentSecurity Defense,North China Electric PowerUniversity,Hebei Baoding 071003,China) The fixed-time stepmethod isoften used to solve the transientelectric field problem of the converter transformerunderpolarity reversalvoltage,whichoften choosessmallersteps in order to ensureaccuracy and causes largeamount of calculation.In order to effectively reduce the com putationalcost,avariablestep-sizeexplicitRunge-Kuttamethod decided by the local truncation errorateach timestep isproposed to analyze the transientelectric field underpolarity reversal voltage.With the proposedmethod,a typicalmodelof the converter transformervalvewinding isanalyzed.The results show that the proposed algorithm isable to effectively reduce the computationalcostand can beused to analyze the transientelectric field of theconverter transformerunder polarity reversalvoltage. converter transformer;polarity reversal;transientelectric field;Runge-Kuttaalgorithm;variable time stepsize TM 15 A 1007-2373(2015)02-0005-06 10.14081/j.cnki.hgdxb.2015.02.002 2014-12-10 國家自然科學基金(51407075) 岳嘯鳴(1980-),男(漢族),高級工程師. 數字出版日期:2015-04-16數字出版網址:http://www.cnki.net/kcms/detail/13.1208.T.20150416.1100.010.htm l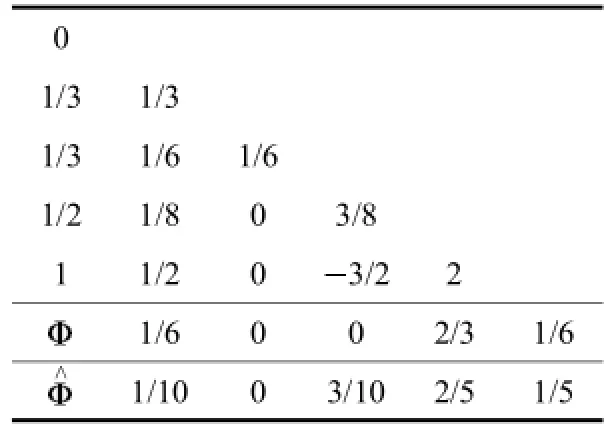

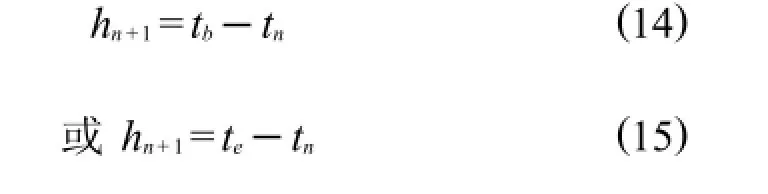
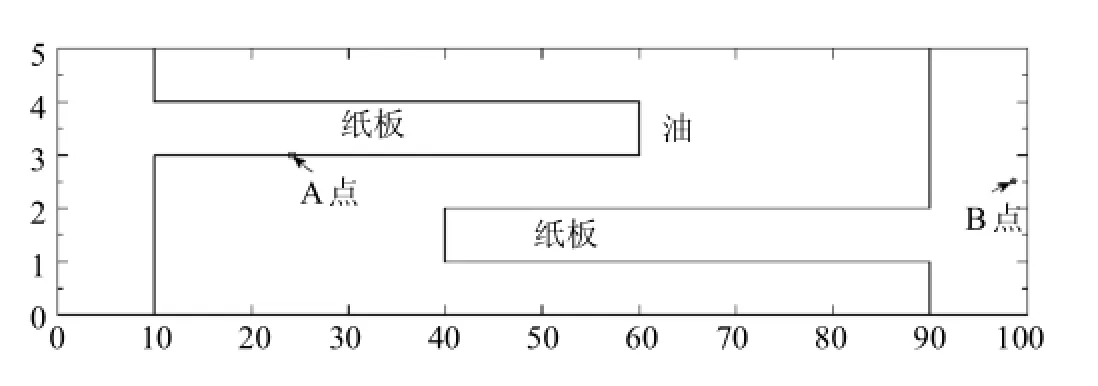
4 換流變壓器閥側繞組典型模型
5 計算結果及分析
6 結論

