地球自轉對彈道導彈被動段落點的影響

蘇 浩

(江蘇自動化研究所，江蘇連云港 222006)

彈道導彈的被動段主要受3 個因素的影響:地球自轉、地球扁率、空氣阻力。在彈道導彈諸元準備中，需分析這3個因素對被動段落點射程的影響及影響方式，以便采取相應的方法來提高諸元準備的速度和精度。對中、遠程彈道導彈，地球自轉是影響落點射程的最重要因素，第二位的是地球扁率，空氣阻力的影響一般僅有幾百米而已。溫羨嶠［1］、謝代華［2］在圓球地球模型上以橢圓彈道理論為基礎分析了地球自轉對彈道的影響，但這些分析存在著一定程度的不足，在較真實地球物理條件下分析探討這一問題具有更為現實的意義和參考價值。本文以正常地球橢球體地球模型為基礎，合理簡化被動段運動微分方程，從動力學角度針對典型射擊情況分析探討地球自轉對被動段落點射程的影響。

1 被動段運動微分方程及簡化

1.1 被動段運動微分方程

彈道導彈的被動段運動通常以質點的動力學問題進行研究，導彈在被動段受空氣阻力、地球引力、由地球自轉產生的柯氏慣性力及牽連慣性力的作用，由質點的動力學理論，發射坐標系中的被動段動力學矢量方程為［3］

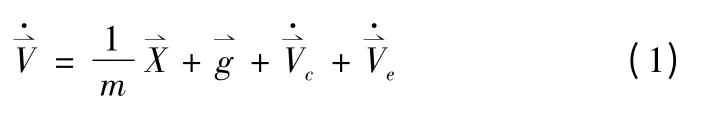
式(1)、式(2)組成被動段彈道運動微分方程組，其為變系數非線性常微分方程組，當給定初始參數，采用數值方法積分，便可求得被動段彈道參數。

1.2 運動微分方程的簡化

彈道導彈的被動段由自由段和再入段兩部分組成，導彈在自由段的射程和飛行時間占全彈道的80% ～90% 以上［4］。在自由段，導彈在相當稀薄的大氣中飛行，空氣阻力遠遠小于其他作用力，通常認為導彈是在真空中飛行的，不考慮空氣阻力的影響;再入段就是導彈重新進入大氣層直至落點的一段彈道，再入段的空氣阻力對導彈的飛行速度有較大影響，而對導彈的射程及飛行時間的影響較小。為了便于分析地球自轉因素對被動段落點射程的影響，同時又保證一定的計算精度，進行如下假設:

a)地球為正常地球橢球體，長半軸aE=6 378 140 m，扁率αE=1/298.257;

b)地球勻速自轉，自轉角速度Ω = 7. 292 115 ×10-5s-1;

c)忽略再入段空氣阻力的影響。

綜上幾點所述，發射坐標系中被動段的標量方程組為

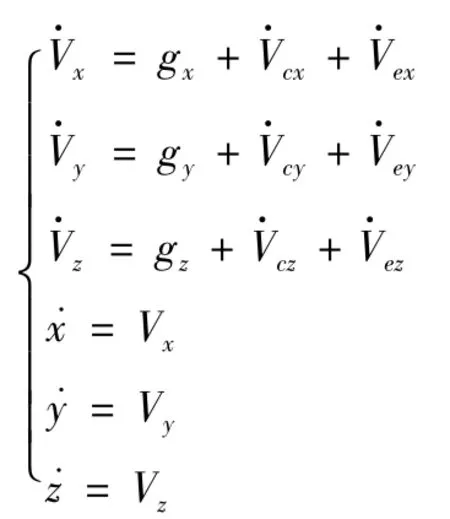
2 主要參數的計算

2.1 柯氏加速度的計算

由理論力學，式(1)中導彈的柯氏加速度為

依據矢量外積運算，柯氏加速度在發射坐標系各軸上的分量為

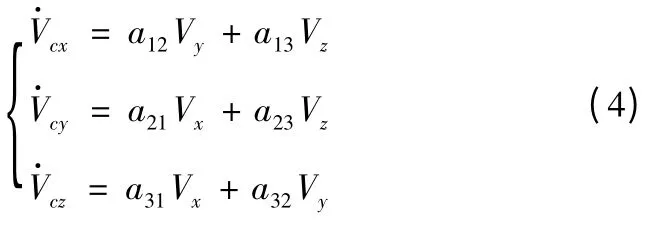
式中:

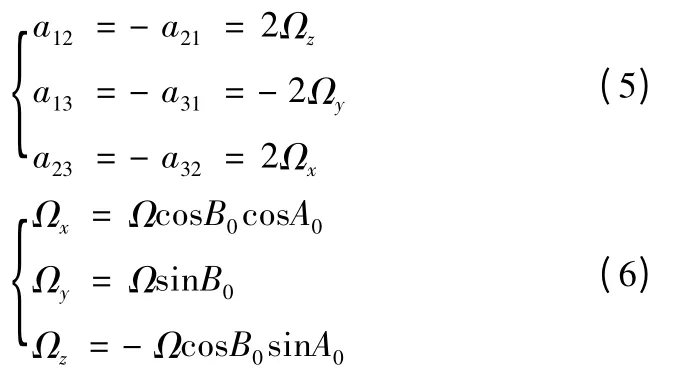
Ωi(i=x，y，z)為地球自轉角速度在發射坐標各軸上的分量;B0為發射點地理緯度;A0為射向。

2.2 牽連加速度的計算

由理論力學，式(1)中導彈的牽連加速度為

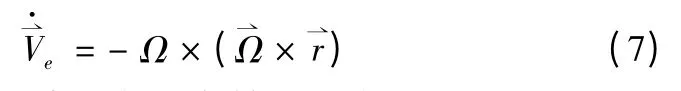
牽連加速度在發射坐標系各軸上的分量為

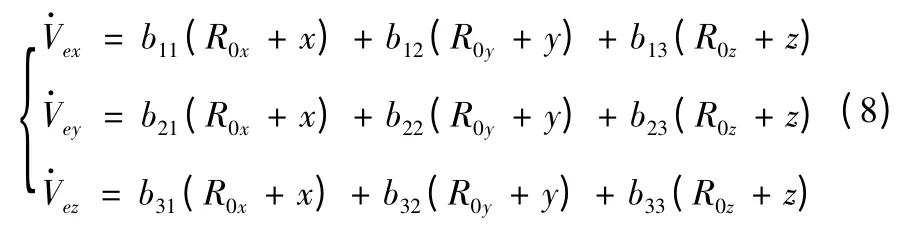
式中:

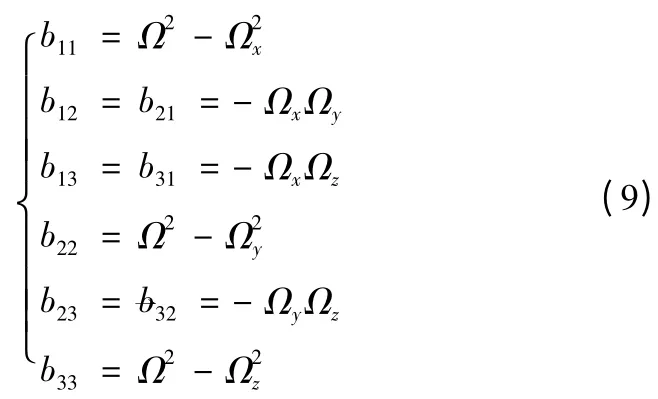
R0i(i=x，y，z)為發射點地心矢徑在發射坐標系各軸上的分量為導彈的地心矢徑。

2.3 落點緯度和經度的計算

2.3.1 落點緯度的計算

落點的地心緯度的計算式為

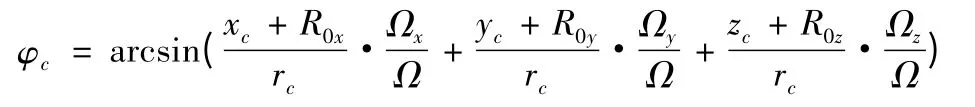
式中:為導彈落點位置在發射坐標系各軸上分量;rc為落點地心距。

地心緯度到地理緯度的轉換公式為［5］

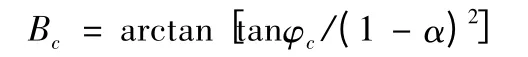
2.3.2 落點經度的計算

發射點與落點之間的經度差為

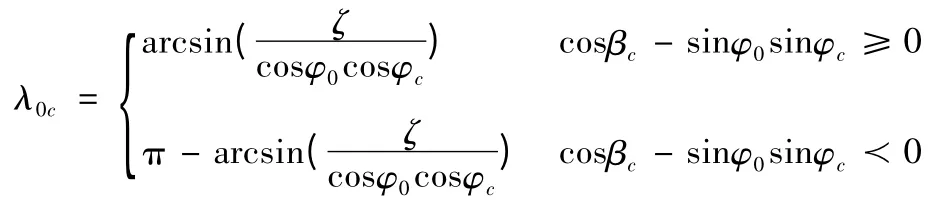
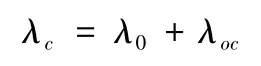
因此落點經度為

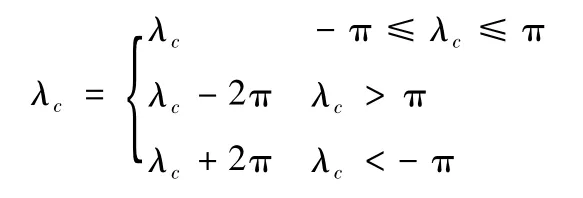
2.4 射程偏差和橫向偏差的計算

在地球自轉因素的作用下，導彈的落點將產生偏差(圖1)，C1為地球自轉因素作用下導彈落點，C2為忽略地球自轉因素導彈落點。C2在射擊平面OC1OE內的投影點為C'，C'與落點C1之間的距離ΔL 為射程偏差，C2與C'之間的距離ΔH 為橫向偏差［3］。

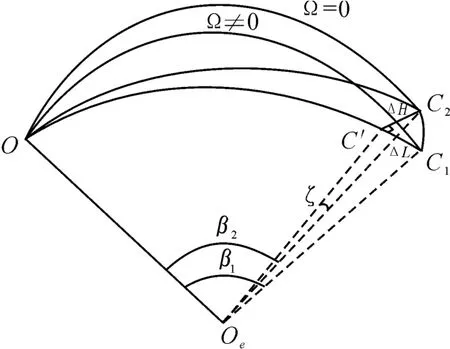
圖1 落點偏差示意圖

落點C1、C2的射程角為β1、β2，相對發射點的球面方位角為ψ1、ψ2，由球面三角形公式，可得:

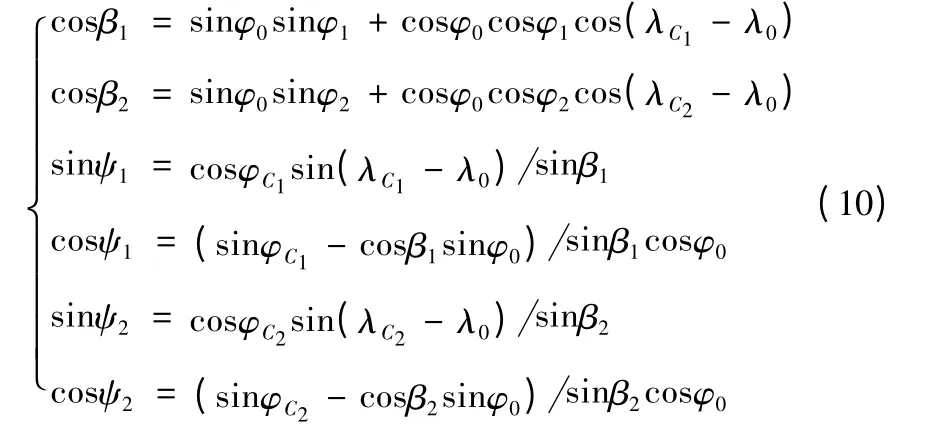
式中:φ0、φ1、φ2分別為發射點、落點C1、落點C2的地心緯度;λ0、λC1、λC2分別為發射點、落點C1、落點C2的經度。

射程偏差ΔL 的計算公式為

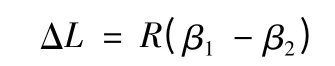
設ΔH 對應的地心角為ζ，則橫向偏差為

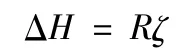
由球面三角形正弦定理

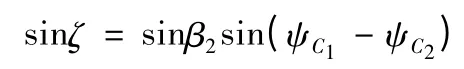
則有

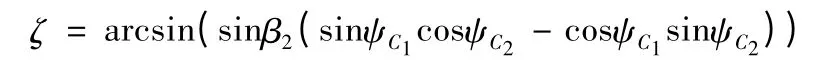
將式(10)的相關計算式代入即可求得ζ。

為計算出更精確的ΔL、ΔH，可用C'處的地心半徑代替地球平均半徑。

3 地球自轉對被動段落點射程的影響分析

地球自轉產生柯氏加速度和牽連加速度，使得導彈在被動段飛行中的受力發生改變，從而使得導彈的落點相對于地球靜止時產生偏差。由式(3)可知，柯氏加速度的大小和方向由2決定，當主動段終點參數所決定的射擊平面與赤道平面重合時，則柯氏加速度在赤道平面內，使得彈道參數發生變化，造成射程偏差，但不會造成橫向偏差。除上述情況外，柯氏加速度作用的結果既會產生射程偏差也會產生橫向偏差，計算結果如表1 所示。

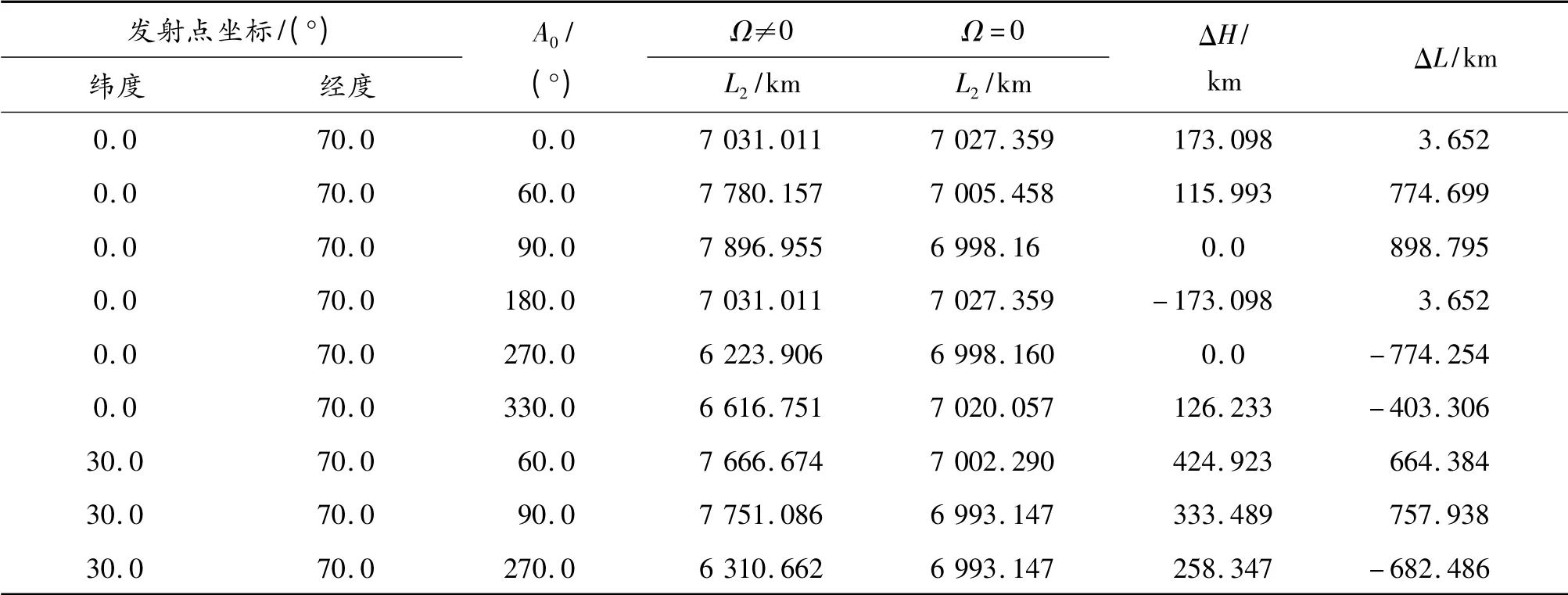
表1 柯氏加速度對落點射程的影響

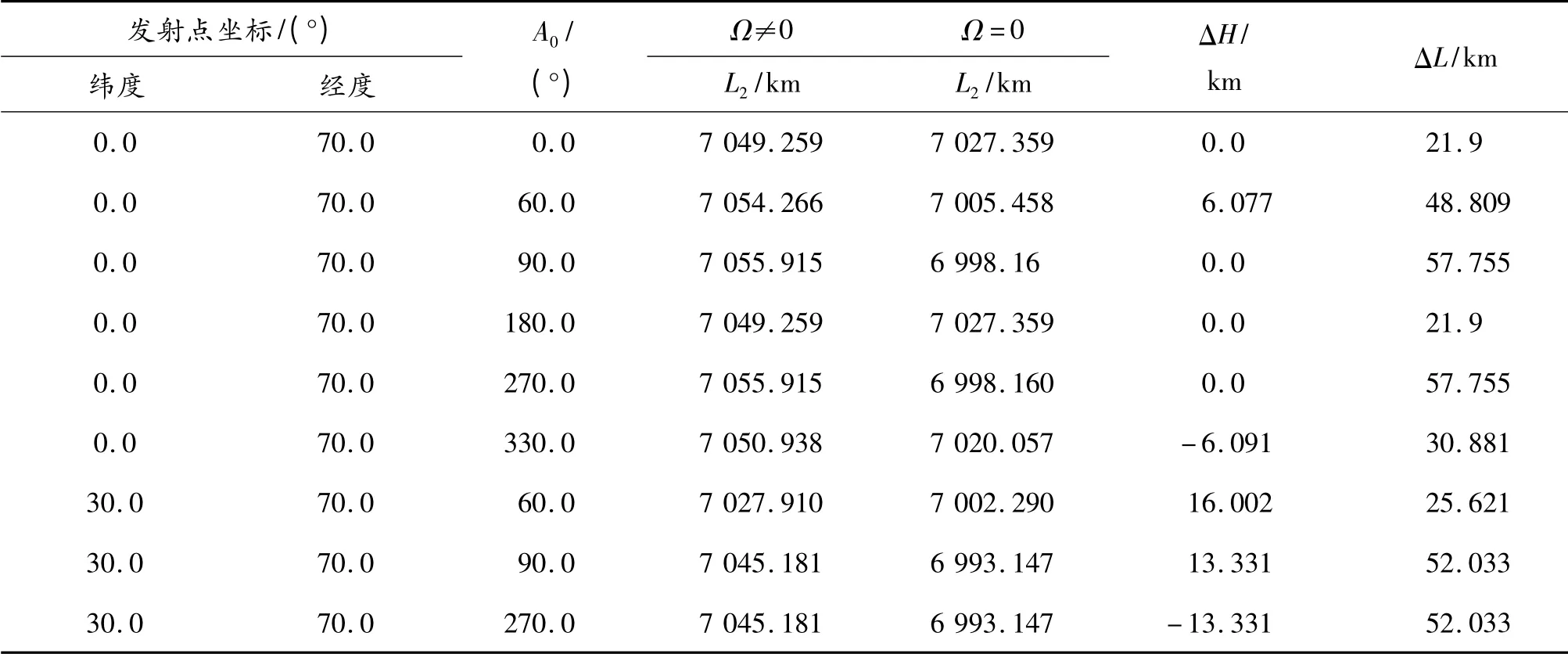
表2 牽連加速度對落點射程的影響

計算結果表明，在地球自轉因素的作用下，當導彈向東射擊時，射程將增加，向西射擊時，射程將減小。下面以導彈發射點位于赤道，主動段彈道終點參數所決定的射擊平面與赤道平面重合這種典型的射擊情況展開分析。

3.1 柯氏加速度對落點射程的影響

導彈向東射擊，B0=0°，A0=90°，由式(5)、式(6)可得

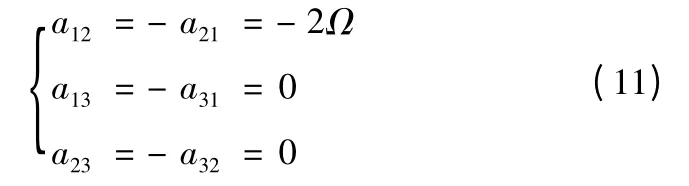
將式(11)代入式(4)，有

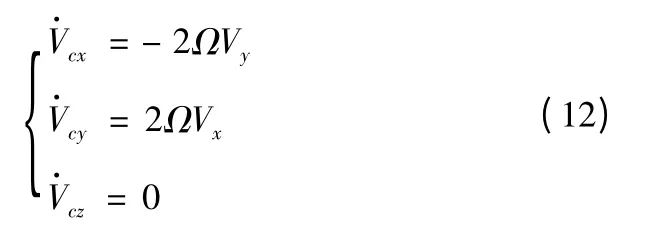
導彈向東射擊時，速度分量Vy在被動段開始飛行不長的一段時間內由正值減小到零，此后Vy為負值且絕對值不斷增大，由式(12)第一式可知，柯氏加速度分量在被動段開始的一段時間內為負值逐步到零，此后為正值，且不斷增大;速度分量Vx在被動段飛行的絕大部分時間內為正值，只有在落點前一段不長的時間內才有可能為負值(射程較大時才會出現負值的情況)，由式(12)第二式，柯氏加速度分量被動段飛行的絕大部分時間內為正值，只有在落地前一段不長的時間內才有可能為負值。從導彈整個被動段的飛行來看，導彈向東射擊時，柯氏加速度總作用的結果將使得彈道高度提高、射程增加，仿真計算結果見表1，圖2 給出了導彈向東射擊，在Ω=0 射程約為7 000 km 時隨飛行時間的變化曲線。

導彈向西射擊，B0=0°，A0=270°，由式(5)、式(6)可得

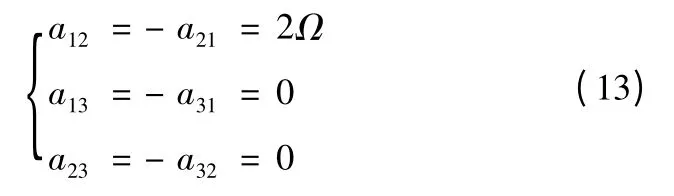
將式(13)代入式(4)，有

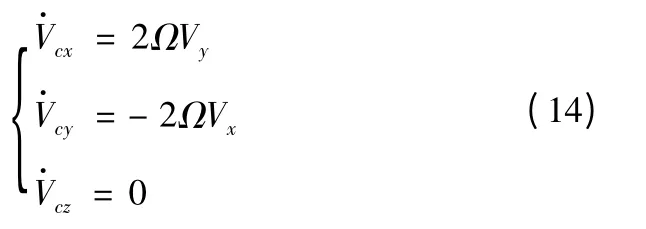
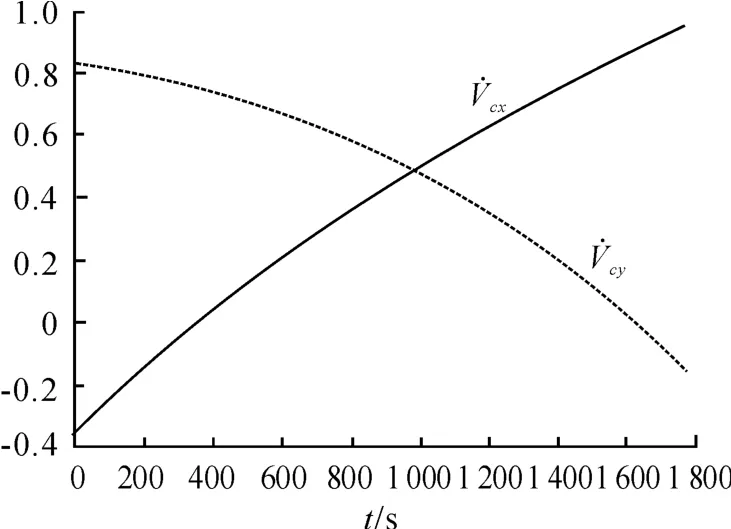
圖2 隨飛行時間變化曲線

導彈向西射擊時，速度分量Vy在被動段開始飛行不長的一段時間內由正值減小到零，此后Vy為負值且絕對值不斷增大，由式(14)第一式可知在被動段開始的一段時間內為正值逐步到零，此后為負值且絕對值不斷增大;速度分量Vx在被動段飛行的絕大部分時間內為正值，只有在落地前一段不長的時間內才有可能為負值，由式(14)第二式，柯氏加速度分量在被動段飛行的絕大部分時間內為負值，只有在落點前的一段時間內才有可能為正值。從整個被動段的飛行來看，導彈向西射擊時，柯氏加速度總作用的結果將降低彈道高度、減小射程，仿真計算結果見表1，圖3 給出了導彈向西射擊，在Ω=0 射程約為7 000 km 時，隨飛行時間的變化曲線。

3.2 牽連加速度對落點射程的影響

由式(6)、式(9)可知，無論導彈向東射擊，還是向西射擊，均有

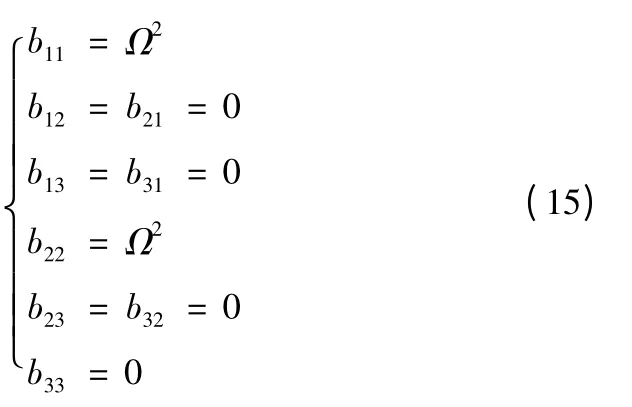
將式(19)代入式(8)，有

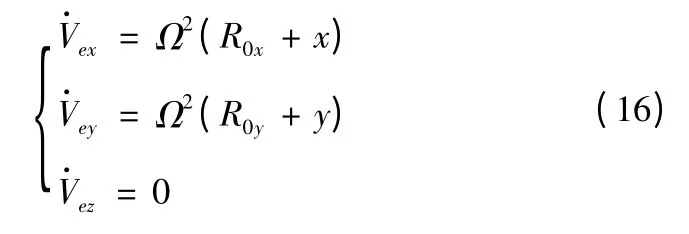
圖3 隨飛行時間的變化曲線

對于中、遠程彈道導彈，在被動段飛行的整個階段R0x+x、R0y+y 均為正值，由式(16)可知在被動段飛行的整個階段為正值，因此，牽連加速度的作用將使得彈道高度提高，射程增加，仿真計算結果見表2，圖4 為導彈向東射擊，在Ω=0 射程約為7 000 km 時隨飛行時間的變化曲線，圖5 為導彈向西射擊，在Ω =0 射程約為7 000 km 時，隨飛行時間的變化曲線。

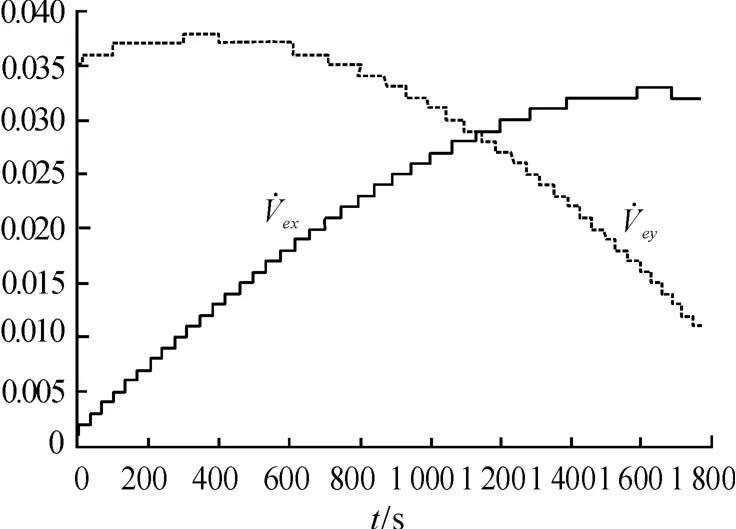
圖4 隨飛行時間的變化曲線

3.3 柯氏加速度與牽連加速度的綜合作用

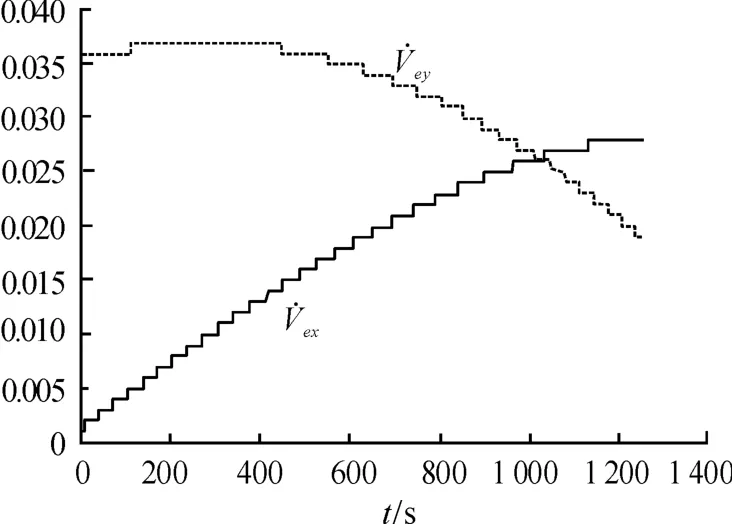
圖5 隨飛行時間的變化曲線

圖6 隨飛行時間的變化曲線

圖7 隨飛行時間的變化曲線

4 結束語

［1］溫羨嶠，高雁翎.地球旋轉對彈道性能影響分析［J］.現代防御技術，2006，34(1):11-15，36.

［2］謝代華.地球自轉對彈道導彈軌道和落點影響分析［J］.航空兵器，2006(1):18-21.

［3］張毅.彈道導彈彈道學［M］.長沙:國防科技大學出版社，1998.

［4］賈沛然.遠程火箭彈道學［M］.長沙:國防科技大學出版社，1993.

［5］肖業倫.航空航天器運動的建模—飛行動力學的理論基礎［M］.北京:北京航空航天大學出版社，2003.