基于EEMD 的聲發射管道泄漏定位檢測

周穎濤，周紹騎，姚遠航，晁文勝

(1.后勤工程學院軍事供油工程系，重慶401331;2. 68099 部隊，寶雞 721700)

管道在油氣輸送過程中，由于老化、斷裂、腐蝕、人為破壞等原因，泄漏時有發生，嚴重威脅人員和財產安全。現有的檢測方法如負壓波法、模型法、神經網絡法等［1］，對于小孔泄漏、緩變泄漏、已發生的泄漏等情況，存在定位精度不高、甚至無法定位的缺點。聲發射法既適用于突然泄漏，也適用于已經發生的泄漏，安裝傳感器時無需在管道上打孔，因此對聲發射管道泄漏檢測定位研究具有重要意義。

在實際檢測中，傳感器接受到的信號包含大量噪聲，直接用原始信號進行計算就會造成較大誤差，現有的信號處理方法如小波包分解［2］、EMD［3］等先后被應用于管道泄漏聲發射定位，但都不能完全解決定位精度不高的問題。為提高定位精度，本文選取集合經驗模態分解(EEMD)作為數字信號處理方法，管道泄漏產生的聲發射信號具有強烈的非平穩特性［4］，EEMD 適用于非平穩隨機信號的分析，通過對分解的信號進行提取和重構，可以更準確、有效地把握信號的特征信息。

1 聲發射定位原理

當管道發生泄漏時，在管內流體從漏孔向外噴射過程中，流體與泄漏孔處管壁的摩擦產生的能量以應力波的形式沿管壁傳播，利用聲發射傳感器采集該應力波信號，通過互相關法計算時差，即可確定泄漏位置。其定位原理如圖1 所示［5］，由泄漏處產生的聲發射信號傳到兩端的傳感器產生一個時間差Δt，Δt=(L2-L1)/C，L1、L2為泄漏處與傳感器1、2的距離，C 為泄漏處產生的聲發射信號沿管壁傳輸的速度，其中

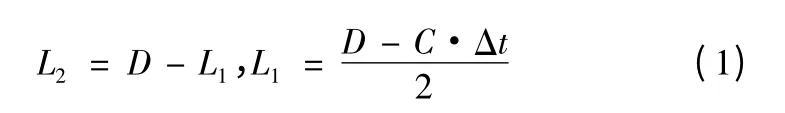
式(1)中D 為兩傳感器之間的距離，只要知道Δt，就可以確定漏孔位置，而對兩個傳感器接收到的信號進行互相關計算就可以得出Δt。其中互相關函數

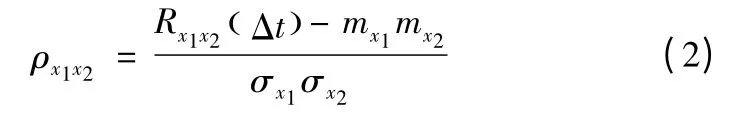
式(2)中:Rx1x2(Δt)為兩信號的互相關函數;mx1、mx2為兩信號的平均值;σx1、σx1為兩信號的均方差。ρx1x2最大時對應的Δt 為所求的時間差，進而可以計算出泄漏的位置。泄漏信號沿管壁傳輸速度為［6］

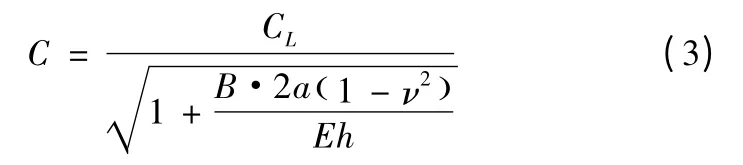
式(3)中:CL為縱向體速度;E 和ν 分別為彈性模量和泊松比;B 為體積模量;h 為管的厚度;a 為水管內經。

圖1 泄漏定位檢測原理

2 EEMD 信號分析方法

EEMD 算法為改進的EMD 算法，這是一種自適應分頻方法，不必像小波包分解那樣既要考慮小波基的選擇又要考慮分解尺度［2］，可以較好地解決聲發射泄漏信號的多模態問題，具有良好的適應性和準確性，近年來被大量應用于語音信號處理和機械故障診斷等領域［7］。

2.1 經驗模態分解(EMD)算法

1998年，美籍華人Norden E. Huang 等［8］提出了本征模態函數(Intrinsic Mode Function，IMF)的概念，以及將任意信號分解為一組本征模態函數的新方法——經驗模態分解(Empirical Mode Decomposition，EMD)。EMD 本質上是一種將時域信號按頻率尺度分解的數值算法，可以根據被分析信號自身的特點，自適應地選擇頻帶，將原始信號分解為若干個IMF 分量和殘余分量，具有直觀、直接、后驗以及自適應性，適用于非平穩信號的分析。

2.2 集合經驗模態分解(EEMD)算法

EMD 過程中，當數據不是純的白噪聲時，分解中的一些時間尺度會丟失，這時就會造成分解的混亂，即模態混疊［9］。為了解決這個問題，Wu 和N.E.Huang 等［9］提出了集合經驗模態分解(Ensemble Empirical Mode Decomposition，EEMD)法，其具體過程為

1)在目標數據上面加入白噪聲序列;

2)將加入白噪聲的序列分解為IMF;

3)每次加入不同的白噪聲序列，反復重復步驟1)、2);

4)把分解得到的各個IMF 的均值作為最終的結果。

2.3 EEMD 算法應用于聲發射管道泄漏定位

由于管道泄漏聲發射信號中包含有大量的噪聲，如果用EMD 法對信號進行分解，就會遇到泄漏信號和頻段接近的干擾噪聲混疊在一起的現象，即模態混疊現象，通過互相關法進行漏點定位時，就會產生誤差。而EEMD 方法在信號分解過程中通過添加高斯白噪聲，使頻段相近的信號分離，可以得到更準確的分解結果，進而提高定位精度。具體步驟如下:

1)對1#、2#傳感器測得的信號x(1)、x(2)進行小波去噪［10］得到信號s(1)、s(2)。實際測得的信號包含大量噪聲，小波去噪使信號更加平滑，不僅可以減少噪聲的干擾，而且可以有效減少EEMD 的運算時間。

2)通過對信號s(1)、s(2)添加高斯白噪聲，進行EEMD分解，得到兩組IMF。此過程中要合理選擇高斯白噪聲的均方差，如果均方差偏大，會埋沒原始信號，分解出的IMF 會明顯帶有噪聲;如果均方差過小，在分解過程中會使添加的噪聲信號逐步分散在IMF 中，影響低頻部分的分解。本文選取待分解信號s(1)、s(2)均方差的0.1 倍分別作為所添加高斯白噪聲的均方差。

3)對分解的兩組IMF 分別進行選擇性重構。觀察分解的兩組IMF，根據管道泄漏聲發射信號非平穩、隨機性的特點，選取有效的IMF 分別進行信號重構，重構后的信號為h(1)、h(2)。

4)對重構后的信號進行互相關分析，求出時間差，確定泄漏位置。運用Matlab 的xcorr 函數對h(1)、h(2)進行互相關分析，求出h(1)、h(2)互相關序列最大值對應的序列延時矢量Bm。傳感器采樣頻率為Fs，波速為C，則信號h(1)、h(2)的時間差Δt=Bm* C/Fs，測量得到兩傳感器之間的距離為D，通過式(1)即可確定泄漏位置。

3 計算機仿真分析

為驗證EEMD 算法相比EMD 算法的優越性，本文選取如圖2 所示的一組典型信號序列，該信號由一路幅度逐漸增大的正弦信號和7 路頻率依次降低、幅度為1 的信號及趨勢量疊加而成。分別采用EMD 和EEMD 方法分別對上述疊加信號進行分解;EEMD 過程中，所加高斯白噪聲相對均方差為0.1，總體平均次數設為500，最大單次循環數設為5 000，分解結果如圖3 所示。

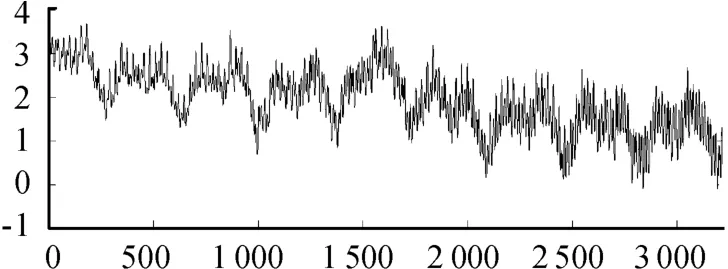
圖2 待分解仿真信號

從圖3 中可以看出，EMD 的結果中IMF 分量存在模態混疊現象，與實際信號相差很大。而EEMD 分解得到的IMF從高頻到低頻依次分布，所得到的信號更加平滑，更接近真實信號，較好地克服了模態混疊現象。

4 實驗分析

模擬管道鋪設了6 m×7 m 長的野戰輸油管線進行輸水實驗，管道外徑102 mm，壁厚2.5 mm，管材為10 號帶鋼，管內水壓為0.06 MPa。采用德國Vallen 公司生產的AMSY-5(M16 -2)型16 通道聲發射儀采集信號，采樣頻率設為2 MHz，采樣點數為10 000 點。1#傳感器和2#傳感器采集到的信號x(1)、x(2)如圖4 所示。

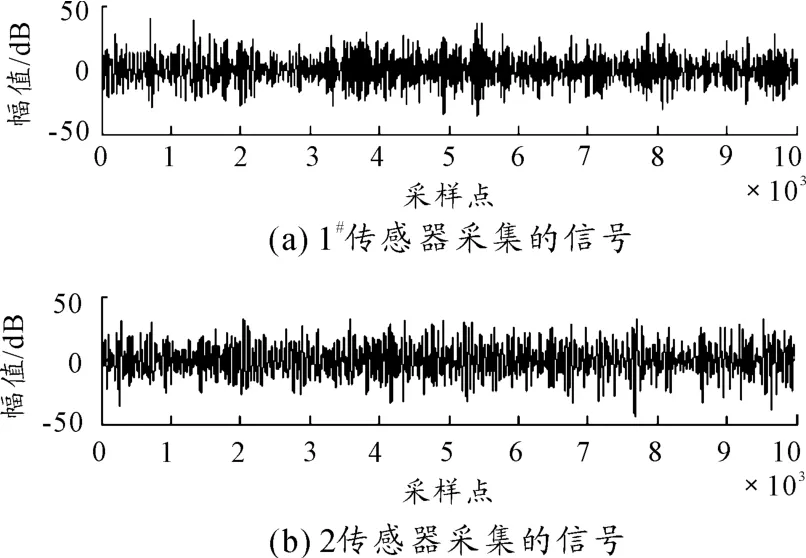
圖4 傳感器采集的信號

由于實驗現場環境含有大量的噪聲(如泄漏水流、振動噪聲、電子儀器帶來的噪聲等)，對原始信號直接進行相關分析會產生較大的誤差。1#和2#傳感器接收到信號x(1)、x(2)經小波去噪，小波基選擇dmey 小波，分解尺度選擇3 層，去噪后的信號h(1)、h(2)如圖5 所示。

圖5 信號經小波去噪后的結果

通過加入相對均方差為0.1 的高斯白噪聲，將信號h(1)、h(2)經EEMD 分解，結果如圖6 所示。

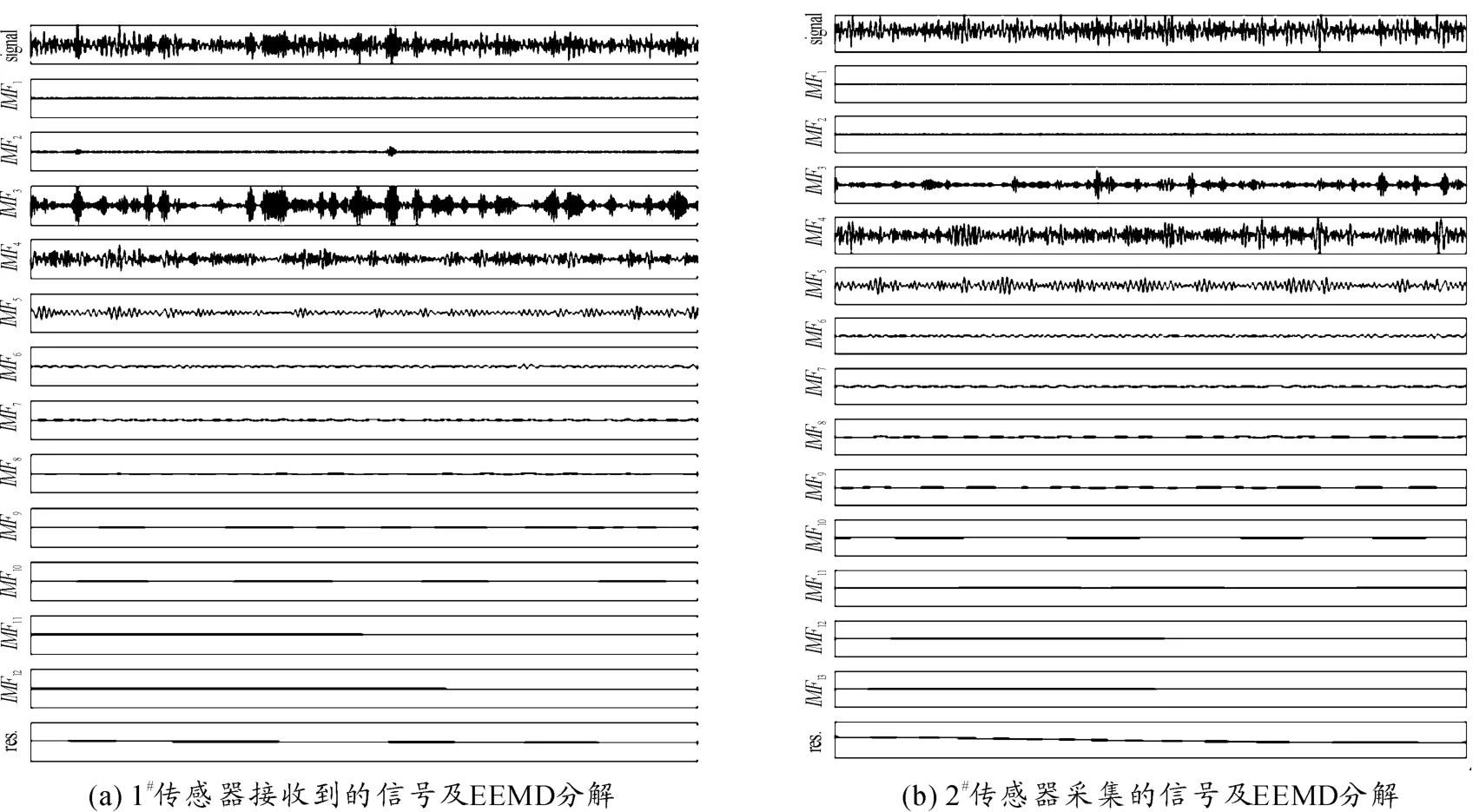
圖6 1#和2#傳感器采集的信號及EEMD 分解

分解得到的IMF 組代表了信號的內在特征，Wu 和Huang［11］用實驗的方法證明了分解過程具有二進濾波的作用。管道泄漏AE 信號具有典型的非平穩特性，根據這一特征，對分解后的IMF 進行分析可獲得信號中更豐富的波動信息。因此，可以利用分解得到的具有典型管道泄漏聲發射特征的IMF 分量對信號進行重構，恢復被干擾的真實信號，而對于剩余的IMF，如果干擾的成分較突出，可以直接將其去除。由于殘余分量是單調的，且代表了信號的整體趨勢，所以對AE 信號的分析作用不大，因此可不考慮殘余分量的影響。

從圖6 可以看出，EEMD 較好地將所測得的信號進行了分解，在分解得到的兩組IMF 中，IMF1、IMF2、IMF6 及其后面的分量幅值很小，對AE 信號的分析影響較弱，故不考慮。分量IMF3 ～IMF5 呈具有沖擊性質的AE 信號的典型特征，因此為有效的IMF 分量。選取IMF3 ～IMF5 三個本征模態函數進行重構，重構后的信號h(1)、h(2)如圖7 所示。

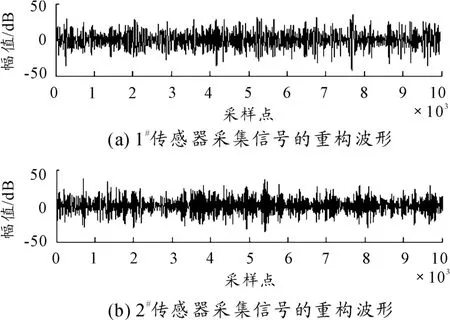
圖7 傳感器采集信號的重構波形

對重構后的信號進行相關分析，得到泄漏點與1#傳感器的距離為17.432 m，實際距離為18.00 m，誤差為3.16%。為進行比較，分別對原始信號、EMD 分解后的重構信號、EEMD 分解后的信號進行互相關分析，計算得到泄漏點距離1#傳感器的位置如表1 所示。

表1 根據不同方法計算的泄漏點位置

5 結束語

為提高管道泄漏聲發射檢測的定位精度，根據管道泄漏AE 信號非平穩、隨機性的特點，選取了EEMD 對信號進行分析:將兩個傳感器采集到的信號依次進行小波去噪和EEMD分解，對分解結果進行信號重構，通過互相關法進行時差計算和漏點定位。運用計算機仿真的方法，對一組典型的模擬信號分別進行EMD 和EEMD，仿真結果表明EEMD 比EMD具有更強的信號分解能力。通過實驗，將所測得的聲發射信號進行小波去噪，添加均方差適合的高斯白噪聲進行EEMD，得到了分解后的兩組IMF 分量。去除IMF 組中的干擾成分，篩選出具有現實物理意義的IMF 分量對兩路信號分別進行重構，進而確定時差和漏點位置。實驗表明:EEMD 比EMD 計算出的結果更為準確，漏點定位精度更高。

［1］陳華波，涂亞慶.輸油管道泄漏檢測方法綜述［J］.管道技術與設備，2000(1):38-41.

［2］史烈，張光新，周澤魁，等.基于聲發射的輸油管線破壞點定位方法研究［J］. 浙江大學學報:工學版，2005，39(3):322-325.

［3］孫立瑛，李一博，靳世久，等.基于小波包和HHT 變換的聲發射信號分析方法［J］.儀器儀表學報，2008，29(4):1577-1582.

［4］《國防科技工業無損檢測人員資格鑒定與認證培訓教材》編審委員會.聲發射檢測［M］.北京:機械工業出版社，2004.

［5］LOU Y L，LIU G F，LI Z X.A general approach for optimal kinematic design of parallel manipulators［C］//New Orleans，LA:IEEE Proc Int Conf on Robot Automat.2004:3659-3664.

［6］PINNINGTON R J，BRISCOE A R.External applied sensor for axisymmetric waves in a fluid filled pipe［J］.Journal of Sound and Vivration，1994，173(4):503-516.

［7］Huang N E，Shen S S.Hilbert-Huang transform and its applications［M］.World scientific publishing co pte ltd，2014.

［8］Huang N E，Shen Z，Long S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proc.R.Soc.Lond，1998，454A:903-993.

［9］Wu Z，Huang N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method［J］.Advances in adaptive data analysis，2009，1(1):1-41.

［10］劉明才.小波分析及其應用［M］. 北京:清華大學出版社，2013.

［11］Wu Z，Huang N E.A study of the characteristics of white noise using the empirical mode decomposition method［J］.Proc.R.Soc.Lond，2004，460A，1597-1611.