艦炮彈藥儲存可靠壽命計算方法

趙 翀，馬 野，董彩霞，張熹濤

(1.海軍大連艦艇學院 a.研究生管理大隊;b.艦炮系，大連 116018;2.西安理工大學自動化與信息工程學院，西安 710048)

艦炮彈藥是艦炮武器系統的核心，是完成作戰任務的最終手段。艦炮彈藥作為重要的軍用物資，消耗量和需求量大，需要有充足且長期的儲備。然而在儲存期間，受儲存條件或彈藥本身設計工藝等因素的影響，儲存質量會隨之下降，因此對艦炮彈藥的儲存可靠壽命進行預測是當前急需研究的問題。由于艦炮彈藥的特殊性，試驗樣本不能重復使用，加之經濟性等原因，在進行可靠性試驗時不可能采用大量成批樣本進行試驗，因此不宜使用傳統可靠性分析理論，但符合小子樣情況，需要運用小子樣理論。常見用的小子樣可靠性評價方法有置信區間法、Bayes 方法、Fiducial 方法、近似正態方法、信息熵法和矩擬合方法等［1］。其中Bayes 方法便于利用先驗信息、節約時間成本、結果準確性高而被廣泛使用［2，3］。

1 艦炮彈藥儲存可靠壽命

1.1 艦炮彈藥儲存可靠性

艦炮彈藥儲存可靠性是指彈藥在規定的儲存條件下和規定的儲存時間內，保持規定功能的能力，是衡量彈藥質量優劣的重要指標［4］。

儲存條件是指彈藥儲存的自然環境條件和人為環境條件。自然環境條件主要指儲存地區的溫度、濕度、空氣環境等外在環境;人為環境條件主要指包裝運輸、儲存地點及周邊環境等環境。儲存時間一般是指彈藥從出廠開始計算直至儲存到某一時刻的時間。規定功能是指根據使用目的而賦予彈藥的各種功能，主要包括保證安全和可靠作用兩方面的若干項具體功能。

衡量艦炮彈藥的儲存可靠性的參數是艦炮彈藥的儲存可靠度。儲存可靠度是指艦炮彈藥出廠后，在規定的儲存、維護條件下，到規定的儲存時間仍能通過鑒定試驗的彈藥檢測合格率［5］。

1.2 艦炮彈藥儲存可靠壽命

艦炮彈藥儲存可靠壽命是指在規定的儲存條件下，滿足規定功能要求所對應的最短儲存時間。設T 為儲存壽命，TR為儲存可靠壽命，R 為儲存可靠度，則三者的關系可以概率表示為

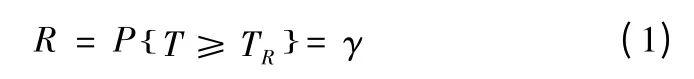
式(1)中，γ 為置信度，表示允許的合格率。

預測可靠壽命的基本方法有2 種:一種是時間序列預測法，該方法不考慮數據產生的原因，只按數據產生的時間順序排列做預測分析，雖然使用范圍很廣，但精度較低。另一種是可靠性統計分析方法，該方法是基于儲存彈藥抽樣試驗觀測數據與彈藥性能指標對比，通過統計分析預測存儲壽命，精度更高，因此本文選用該方法進行艦炮彈藥儲存可靠壽命預測。

可靠性統計分析方法的關鍵是找出作為抽樣的彈藥樣本，通常分批次選取不同儲存時間不同的彈藥進行抽樣，通過獲得對抽樣樣本進行試驗得出試驗數據。具體步驟如圖1所示。

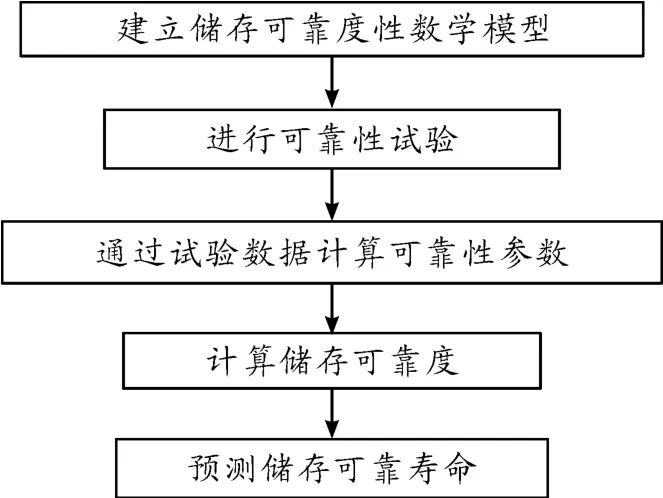
圖1 可靠性統計分析法步驟

2 艦炮彈藥儲存可靠壽命預測

2.1 基本思路

儲存條件下艦炮彈藥產品的可靠性分為固有可靠度R0和條件儲存可靠度Ri(t)。R0表示彈藥固有的可靠度，Ri(t)表示儲存環境條件對產品性能影響的大小。產品儲存可靠度計算公式為

儲存可靠性評估的基本思路如下［6，7］:

對不同年份的產品抽樣進行試驗，根據出廠驗收數據和鑒定試驗數據按二項分布估計產品的固有可靠度和置信下限R0L;依據Bayes 理論計算產品在各已知年份點ti上的可靠度點估計和置信下限RiL。

假定一條儲存壽命分布函數，利用最小二乘法估計分布參數，計算任意時間點的條件儲存可靠度根據式(2)計算產品的儲存可靠度Rs(t)和儲存壽命。

2.2 Bayes 評估方法

依據以上思路，可知在使用Bayes 方法對艦炮彈藥儲存可靠性進行評估時，需要計算彈藥的固有可靠度、各已知時間點的儲存可靠性、條件儲存可靠性函數和任意時刻的可靠性這四個參數。

統計艦炮彈藥的出廠驗收數據和鑒定試驗數據，確定總樣本數和失效數。設n 為總樣本數，f 為失效數，s 為成功數。艦炮彈藥的儲存可靠性實驗是成敗型服從二項分布，則s 對R 的條件概率密度為

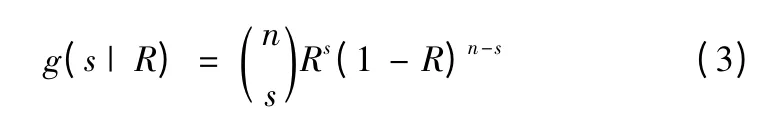
二項分布的共軛先驗分布為貝塔分布，取先驗分布為:

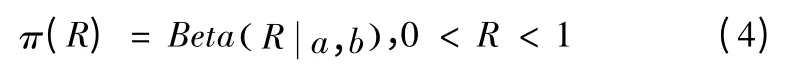
故后驗密度函數為

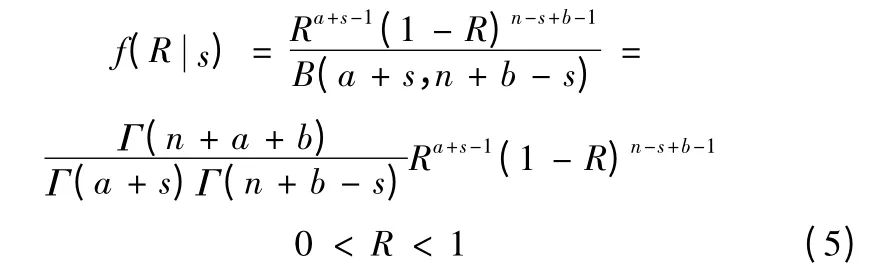
此時R 的期望后驗估計值為

其中，a，b 為待定參數，可由驗前信息確定，即π(R)=B(R，1 +s，1 +f);當無驗前信息時可運用Jeffrey 準則，取a=

單側置信下限RL根據公式

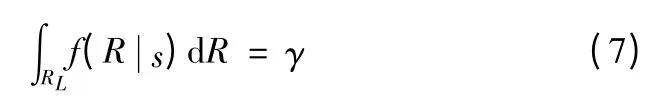
確定。其中γ 為置信度。

1)固有可靠度R0。由于缺少相關出廠數據，根據Jeffrey 準則，取則R0的后驗密度為［8-10］

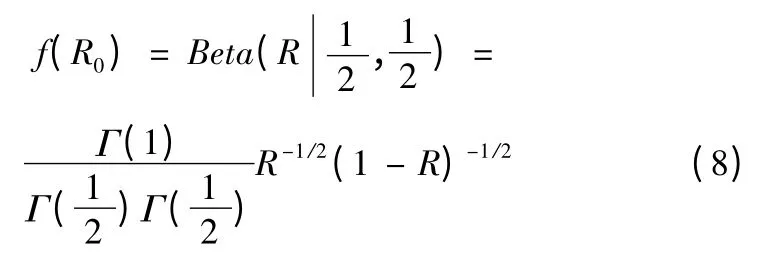
單側置信下限R0L由公式

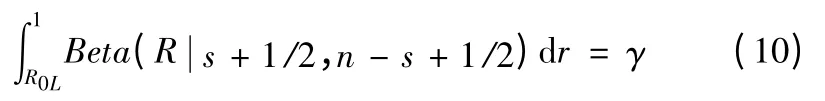
確定。

2)各已知時間點的儲存可靠性。結合艦炮彈藥可靠性數據(ni，fi)，可得可靠度后驗密度為

則可靠度點估計為

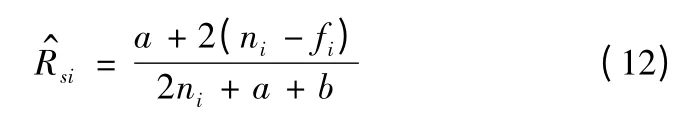
置信下限RiL由公式

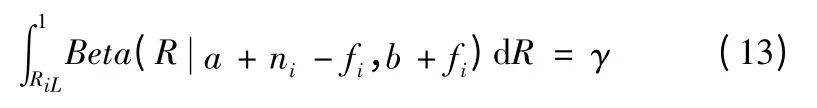
確定。

3)條件儲存可靠度函數。經大量研究實驗證明，艦炮彈藥的壽命分布屬于Weibull 分布模型，可靠度函數為

m、η 的值可以通過最小二乘法估計得［11，12］。

4)任意時刻儲存可靠性評估。根據式(2)可知任意t時刻的彈藥儲存可靠度為

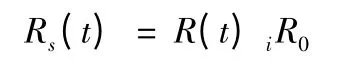
Rs(t)的方差近似為

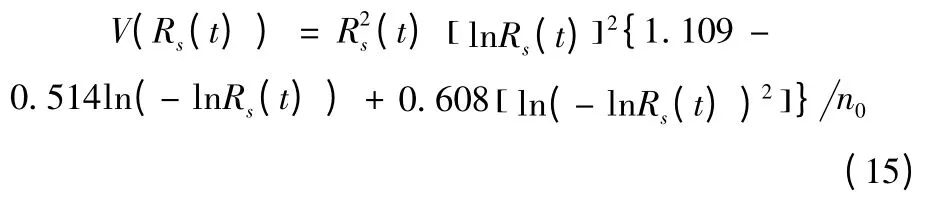
其中，n0為抽樣點樣本量的平均值，因此置信水平為γ 的單側可靠度置信下限為

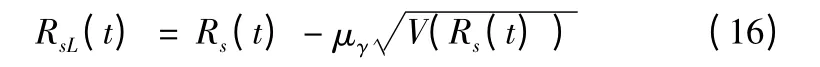
其中，μγ為標準正態分布的γ 的分位數。

5)儲存可靠壽命。設產品允許的最低可靠度為RL，根據式(1)，給定置信度γ 的可靠儲存壽命TR應滿足:

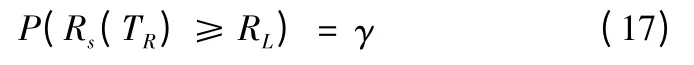
根據正態近似法，認為Rs(TR)近似服從均值為Rs(t)，方差σ2(t)為Rs(t)1 -Rs(t[])n0的正態分布，根據式(14)得:

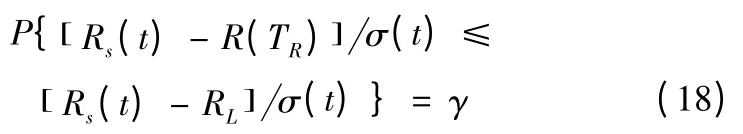
其中

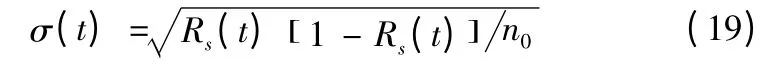
則可靠儲存壽命TR滿足:

3 實例分析

隨機對某倉庫6 個不同年份的相同批次的某型艦炮彈藥進行抽樣檢測，統計數據及固有可靠度如表1 所示。

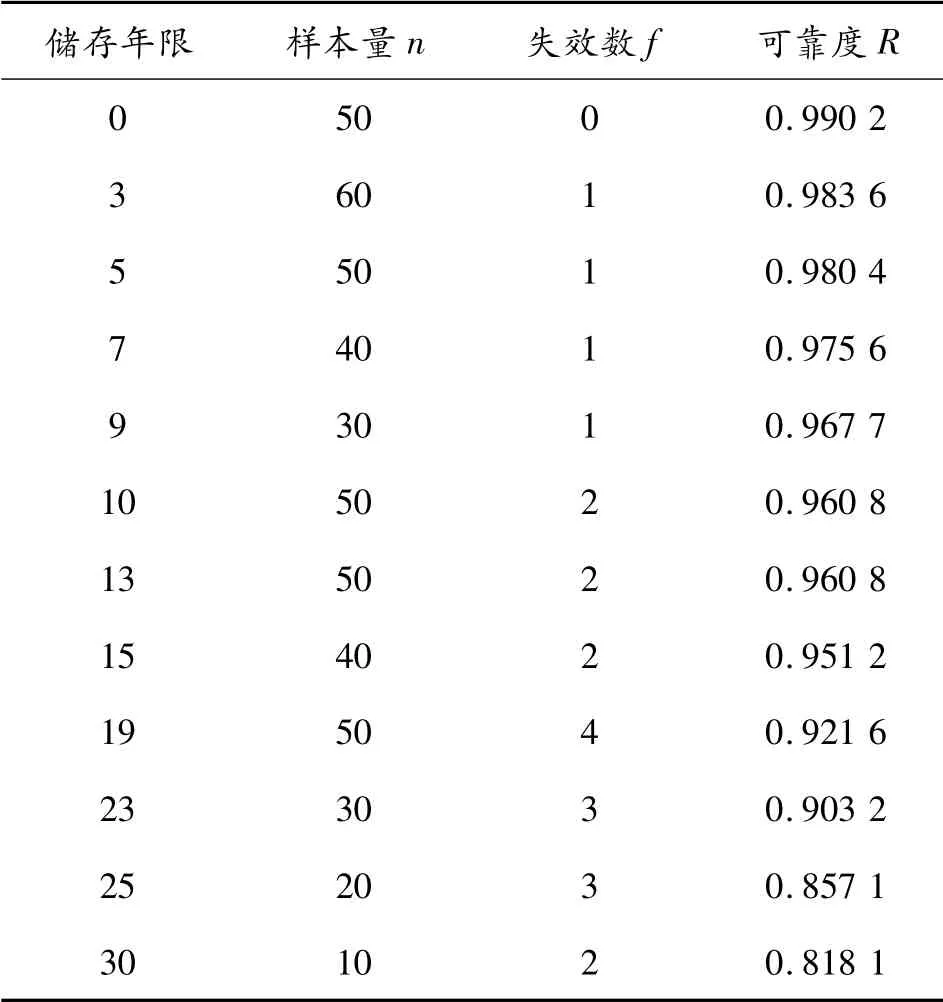
表1 抽樣統計數據

表中，儲存0 a 可靠度認為是彈藥固有可靠度R0，其他為各已知時間點的可靠度Rsi。

根據上述參數，通過Matlab 運用最小二乘法進行曲線擬合，得m=1.3184，η=113.358 0。則

該型彈藥的儲存可靠度為

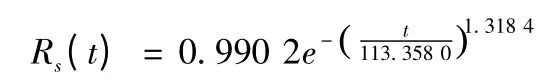
如圖2 所示。

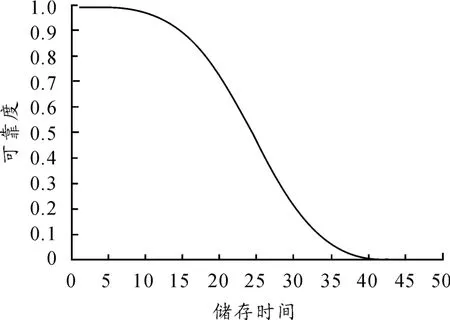
圖2 該型彈藥儲存可靠度

有了儲存可靠度分布，便可以進行可靠性評估，對儲存可靠壽命預測，要求可靠度下限為RL=0.9，取μγ=1.23，根據公式(19)、(20)可計算得Rs(TR)=0.944 8，即

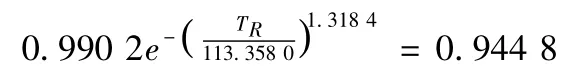
解得儲存可靠壽命TR=11 a。符合實際情況。

4 結束語

針對艦炮彈藥儲存的特殊特點，運用Bayes 方法對彈藥儲存可靠性進行評估，結合壽命分布對彈藥儲存儲存可靠壽命進行預測，最后通過實例驗證其方法的真實性和合理性。對艦炮彈藥倉儲管理等相關工作提供有效的決策支持。

［1］梁慶衛，宋保維，邵成，等. 小子樣產品的可靠性評定［J］.機械設計與制造，2004(1):1-3.

［2］李強，馮元生.疲勞壽命小子樣可靠性試驗評估方法研究［J］.中國機械工程，1996，7(3):93-95.

［3］謝敬芝.Bayes 理論在小子樣產品可靠性分析中的應用研究［D］.合肥:合肥工業大學，2011.

［4］周楓.基于Bayes 方法的海島環境彈藥儲存可靠性研究［D］.長沙:國防科技技術大學，2010.

［5］吳進煌，徐德民，宋貴寶，等.戰術導彈儲存可靠性計算方法研究［J］. 西北工業大學學報，2008，26(3):288-291.

［6］朱威，霍晉堂.電子元器件貯存可靠性評估與預測的貝葉斯方法［J］. 可靠性分析與研究，2007(10):45 -46，67.

［7］陳忠振，許路鐵.彈載光電系統儲存可靠性評估方法探究［J］.價值工程，2013(9):325-327.

［8］宋保維，秦英孝.小子樣產品的可靠性Bayes 評定方法［J］.彈箭與制導學報，1999(2):51-54.

［9］Richard K.Lemaster.Application of Bayesian Reliability Concepts to Cruise Missile Electronic［Z］.AD-A216208，1989.

［10］Theocbre Floropoulos.A Bayesian Method to Improve Sampling in Weapons Testing［Z］.AD-A204365，1989.

［11］金良瓊.兩參數Weibull 分布的參數估計［D］.昆明:云南大學，2010.

［12］劉晗.基于Bayes 理論的小子樣可靠性評定方法研究［D］.長沙:國防科技技術大學，2006.

［13］高萌，王金柱，何學廣. 基于可靠性統計分析法的制導彈藥儲存壽命評估［J］. 裝備環境工程，2013(4):110-113.