層次分析法在復雜裝備維修預計中的應用

郭 濤，劉敬明，介黨陽

(北京宇航系統工程研究所，北京 100076)

在設計和生產過程中，維修性預計是一項重要的工作，它可在試驗、產品制造、乃至詳細設計完成之前，以歷史經驗和類似產品的數據為基礎，對產品可能達到的維修性水平作出評估，這樣可以避免設計的盲目性，縮短研制周期，有助于提高生產效益、降低生產成本。某型復雜裝備系統組成復雜，使用環境相對惡劣，其維修性水平是反應裝備保障性的一項重要指標，維修性預計可以為裝備的維修性設計和試驗策劃提供重要的依據。我國的維修性預計標準在參照了美國的標準基礎上，制定了相應的軍用標準(GJBZ57—1994)［1］。主要的預計方法包括概率模擬法、功能層次預計法、抽樣評分法、運行功能預計法、時間累計預計法及單元對比預計法等［2］。隨著計算機技術的發展，也出現一些新的維修性預計方法，如神經網絡法等［3～4］。目前，這些預計方法大都需要足夠的經驗、試驗數據作為樣本，這對于復雜裝備存在一定的困難。

1 基于AHP 的單元對比預計法簡介

1.1 層次分析法

層次分析法(analytic hierarchy process，AHP)是美國匹茲堡大學教授薩泰于20 世紀70年代提出的一種系統分析方法，是定性分析與定量分析相結合的一種多目標決策方法［5-6］。它將人的經驗和判斷以量化的形式表示，通過簡潔的計算得出各方案的相對重要性排序，從而使復雜的問題明朗化，使決策者的思路條理化、層次化。突出的特點是對于一個復雜問題按照目標、準則、方法措施等分層劃分出來，再把方案兩兩對比，進行評分，然后進行綜合評價，排出優劣次序。層次分析法很好地解決了對復雜問題的評價問題，可以為決策者提供決策依據，是一種成熟的武器系統分析方法。

1.2 單元對比預計法

在組成系統或設備的單元中，以某個維修時間已知的或能夠估測的單元作為基準，其他的單元通過與基準單位的對比，估計出各單元的維修時間，再按維修頻率求均值，從而得到系統或設備修復性或預防性維修時間［1］。

單元對比預計法的預計模型

式(1)中:Mct0為基準可更換單元的平均修復時間;hci為系統或設備中第i 個可更換單元相對維修時間系數;ki為系統或設備中第i 個可更換單元相對失效率系數，ki=λi/λ0。

1.3 AHP 單元對比法

基于AHP 的單元對比法可以對復雜系統首先利用層次分析方法將問題層次化，根據問題的性質和要達到的目標，把問題按照組成因素以及各因素的相互關系加以組合，形成一個層次分明的結構模型。通過兩兩比較依次確定下一層對上一層相對重要性權值，最終確定結構模型中最底層相對于最高層相對重要性權值，這樣就可以確定系統或設備在某維修級別的可更換單元的平均維修時間相對比值［7～8］。

由各可更換單元的權向量求各可更換單元相對比重向量

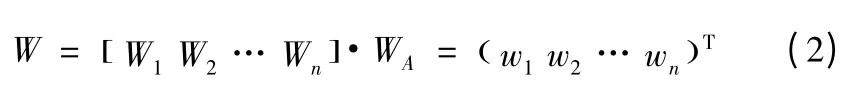
以第j 個可更換單元作為基準單元，可以得到系統或設備的平均維修時間的預計值

式(3)中:Mctj為第j 個可更換單元作為基準單元的平均維修時間;ωij為系統或設備中第i 個可更換單元相對第j 個可更換單元相對維修時權重系數，ωij=wi/wj;λi為第i 個可更換單元的失效率(估計值)。

比較單元對比法與AHP 的單元對比法進行的設備平均維修時間的計算方法，兩種方法的差異主要在于分別采用了設備維修相對時間系數與設備維修相對權重系數。由于設備的平均維修時間是維修性指標量化的重要指標，在AHP單元對比法中，以設備平均維修時間為考慮因素進行單機的權重比較來建立判斷矩陣，得到的系統或設備平均維修時間預計值具有較高的準確性。

2 某型裝備修復維修時間預計

2.1 結構模型

根據對某型復雜裝備組成及維修性特點的初步分析，將影響裝備維修性的影響因素按層次進行排列，將裝備維修性的結構模型分成3 層(圖1)，包括目標層、指標層及評估對象層，其中把維修性作為目標層，將維修性的要求(包括可達性、可測試性等)作為中間的指標層，將裝備分系統及各單機作為評估的對象層。

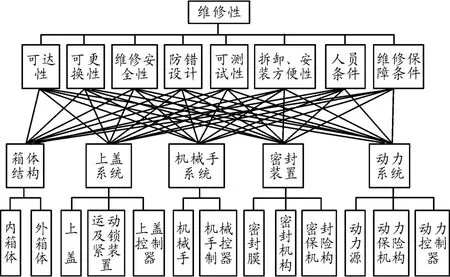
圖1 某型裝備維修性層次的結構模型

2.2 評價矩陣及權向量的確定

在建立層次分析結構模型后，逐層對各元素進行兩兩比較，最常采用的是1 ～9 尺度，具體見表1。

表1 兩兩比較重要性等級及賦值

根據表1 和圖1，首先建立各維修性要求(中間層)對維修性(目標層)的相對重要程度的判斷矩陣如下:

判斷矩陣A 的一致性檢驗CRA=0.002 97 ＜0.1，滿足一致性的要求。則維修性要求相對維修性的權重向量WA為

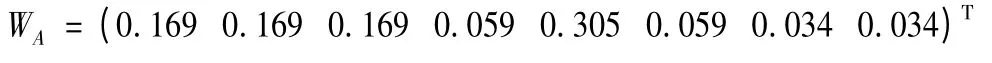
其次分別建立裝備系統級(對象層)對應維修性要求的判斷矩陣如下:

分別計算各判斷矩陣的一致性檢驗

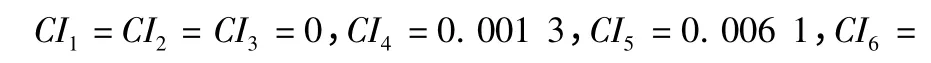
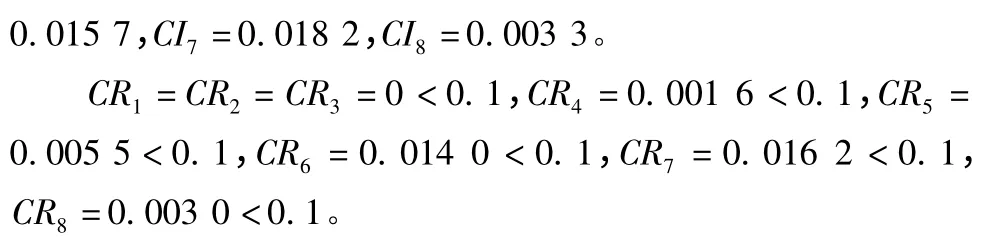
則裝備系統級(評價對象)相對維修性要求的權重向量分別為

計算裝備結構模型的組合(第3 層相對第1 層)一致性檢驗

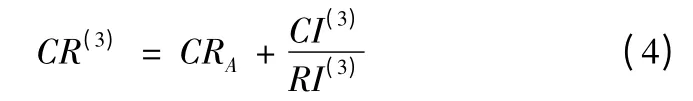
得到:CR(3)=0.0029 7 +0.003 6 =0.006 6 ＜0.1，可認為滿足組合一致性要求。

則裝備系統(評價對象)相對維修性的權重向量為

分別建立裝備單元設備對應裝備分系統的判斷矩陣:

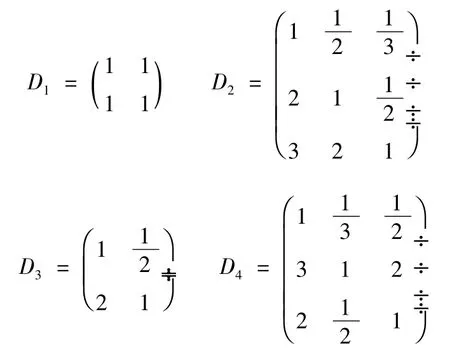
各矩陣的一致性檢驗結果如下:CR1=CR3=0 ＜0.1，CR2=CR4=0.007 9 ＜0.1 滿足一致性要求。

可裝備單元設備對應裝備分系統的權重向量分別為

則裝備單元設備相對比重向量W(相對于維修性)為

從裝備單元設備的相對比重向量值，可以清楚地得出單元設備在維修性指標的重要程度，權重大小直接影響著裝備的維修性的好壞，在裝備維修性設計中著重解決權重較大的單元設備的維修性問題，對提高裝備的維修性具有事辦功倍的效果，可以為裝備的維修性設計和策劃提供依據。

2.3 平均修復維修時間

已知裝備各更換單元失效率分別為

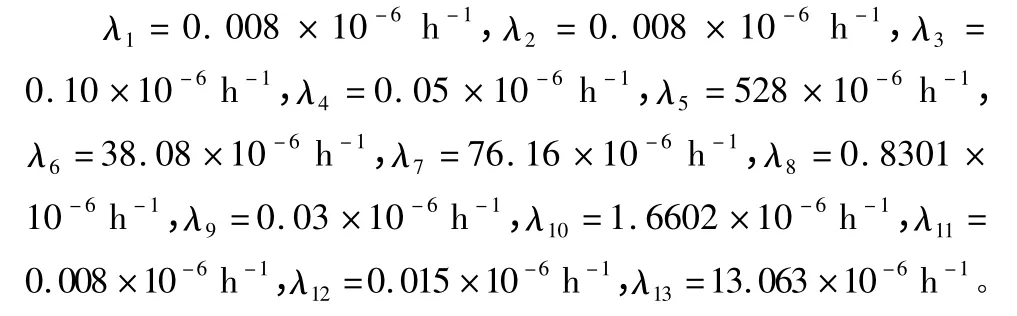
在裝備單元設備中，由于上蓋控制器的維修作業數據較全，所進行的維修性試驗也相對較多，并且失效率也最高，從歷史經驗和試驗數據可知上蓋控制器的平均修復維修時間大約為選取上蓋控制器作為基準單元，根據AHP 的單元對比方法，可以得到裝備的平均修復性維修時間預計為

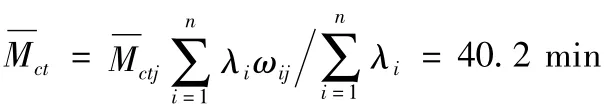
根據我國軍標的時間積累預計方法，該裝備在任務剖面的修復性維修時間的預計值為36.6 min。采用AHP 單元對比法預計的結果與采用時間積累預計方法得到的結果相差較少，說明了采用AHP 單元對比法的維修性的預計結果具有較好的準確性。

在AHP 單元對比法中，基準單元的選取非常重要，選取相似或相關設備試驗數據多、失效率大的單元設備作為基準單元有利于提高預計結果的準確度;同時，在維修性設計時應策劃或安排后續該類單元設備的維修性試驗進行驗證及數據積累。

從平均修復性維修時間預計的公式可以看出，影響設備該指標的因素主要是設備的單元失效率及相對權重系數，重點解決減少裝備中相對權重系數較高設備的單元設備失效率是提高裝備維修性設計的關鍵及方向，AHP 單元對比法為其提供了設計和策劃的依據。

3 結論

本文采用AHP 單元對比法對某型復雜裝備修復性維修時間進行預計，經研究得到如下結論:采用AHP 的單元對比預計方法進行的復雜裝備維修性預計結果具有較好的準確性;AHP 單元對比預計方法可以為復雜裝備維修性設計提供定性和定量分析的決策方法，為開展后續維修性的設計、維修性試驗的策劃提供依據;為提高該方法預測的準確性，建立較為準確的判斷矩陣及選擇正確的基準單元是關鍵，需要不斷的試驗數據的積累及專家經驗的積累，才能使預計的結果不斷接近真實;AHP 的單元對比預計法作為一種簡便的決策方法，不僅可以應用在該型裝備的維修性預計和決策中，同樣也可以應用于其他復雜裝備的維修性預計工作中。

［1］GJB/Z 57—1994，維修性分配與預計手冊［S］.

［2］張勝濤，婁壽春，湯陽春.維修性預計方法運用現狀及展望［J］.航空維修與工程，2006(4):47-49.

［3］姜偉，陶鳳和. 人工神經網絡在維修性預計中的應用［J］.武器裝備自動化，2005，24(6):25-26.

［4］賈云獻，陶鳳和.用人工神經網絡BP 算法預計系統維修性［J］.工程設計，1997(3):35-38.

［5］梁慶衛，蔣姍姍，孫天元.層次分析法的水下航行器維修性指標分配方法［J］.火力與指揮控制，2013，38(7):115-118.

［6］曹勤.AHP 層次分析法在設備維修決策中的應用［J］.石油化工設備，2009，38(增刊):97-100.

［7］呂川.維修性設計分析與驗證［M］.北京:國防工業出版社，2012.

［8］宋保維，董博超. 基于層次分析法的維修性預計方法［J］.魚雷技術，2011，19(2):226-230.