紅外尋的導彈舵機舵偏角速率需求分析

李友年，王 霞，陳星陽，鄭鵾鵬

(中國空空導彈研究院，河南洛陽 471009)

紅外尋的導彈輸入噪聲主要有視線角測量噪聲、閃爍噪聲、目標均勻分布機動噪聲。本文從紅外尋的導彈輸入噪聲的角度，利用伴隨分析方法，對舵機舵偏角速率的需求進行了分析。

1 伴隨分析方法

伴隨技術是基于系統脈沖響應的，它能用于分析如導彈尋的回路這樣的線性時變系統。應用伴隨方法，可以得出在特定時間的任何量的確切性能估計，并可以得出所有干擾量對性能的影響信息。

1.1 伴隨系統產生方法

伴隨系統是通過對原始系統按照一定的變換規則加以變換得到的，對于線性時變系統，首先畫出它的狀態變量圖，然后按照以下規則變換［1］:

1)用tf– t 代換原系統中所有變系數的自變量時間t。

2)倒換所有信號的流動方向，并將分支點改為求和點，將求和點改為分支點，則原始系統的輸入端變為新系統的輸出端，原始系統的輸出端變為新系統的輸入端。

即，若原系統的狀態方程如式(1)，則相應的以狀態空間描述給出的伴隨系統的表達式如式(2):

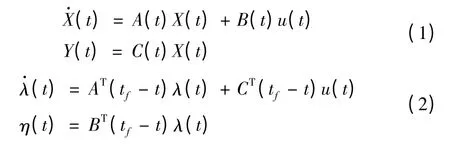
1.2 噪聲系統的伴隨模型

若線性系統的輸入為白噪聲，假定白噪聲的功率譜密度為φ，系統對噪聲的脈沖響應函數為h(t，τ)，可得線形系統對白噪聲均方響應的數學期望［2-3］

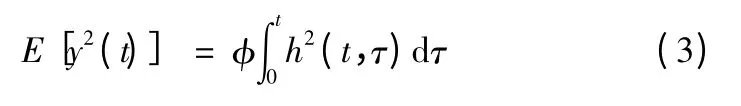
其中:y(t)為線形系統對白噪聲的響應;τ 為脈沖發生時間;t為觀測時間。

根據式(1)、式(2)所述的原始系統與伴隨系統的基本關系，可得

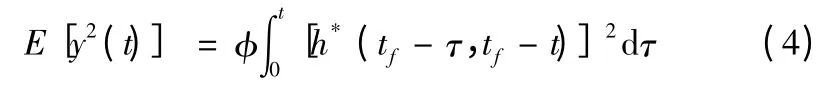
令x=tf-τ，則有

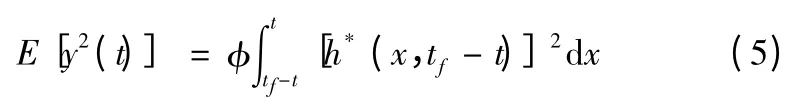
則當t=tf時，有

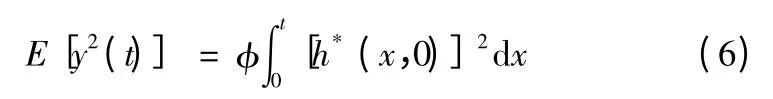
由式(6)可知，當線形系統具有多個確定的白噪聲輸入時，對原始系統的白噪聲輸入變成伴隨系統的輸出，具有隨機輸入的線性系統的伴隨模型與原模型等效關系如圖1 所示。

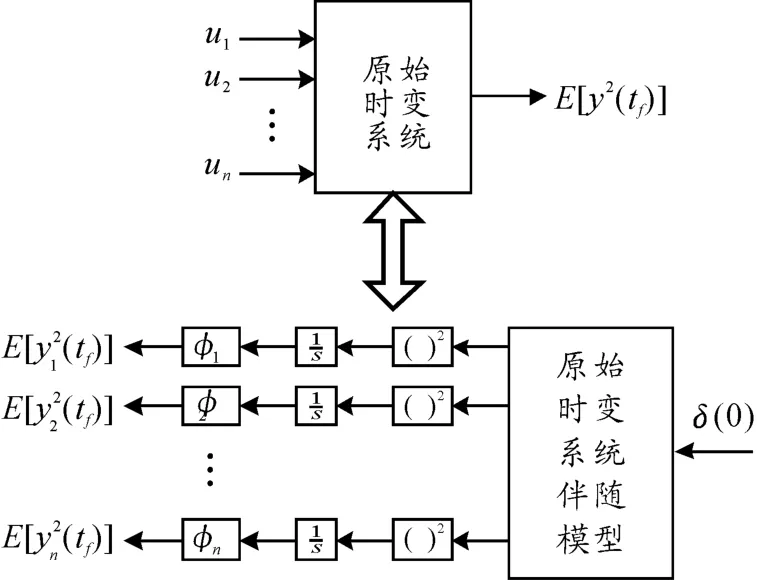
圖1 隨機輸入的伴隨模型與原模型等效關系

2 舵偏角速率需求分析

紅外尋的導彈輸入噪聲主要有視線角測量噪聲、閃爍噪聲、目標均勻分布機動噪聲。

紅外尋的導彈制導系統伴隨模型如圖2 所示。

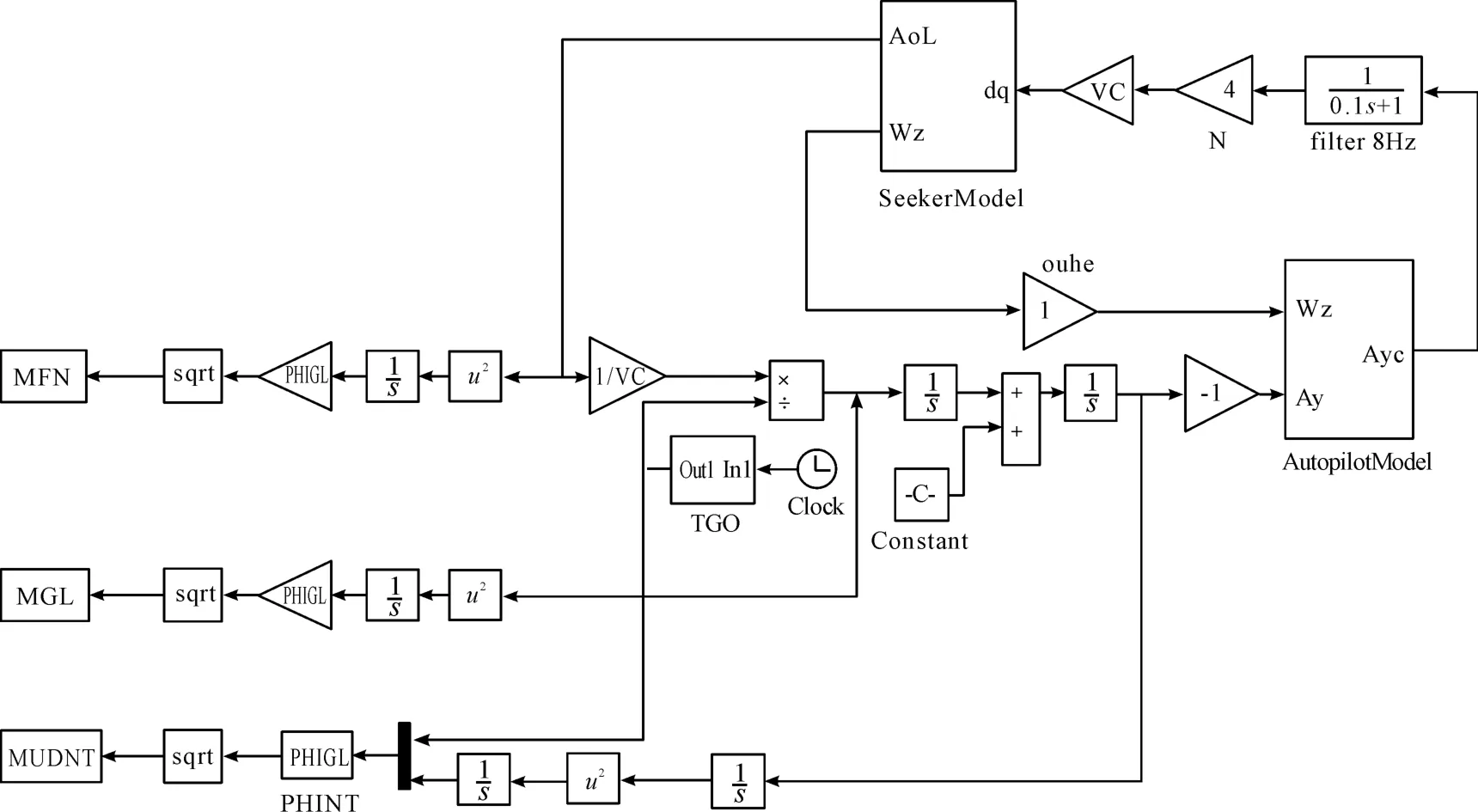
圖2 紅外尋的導彈制導系統伴隨模型

2.1 視線角測量噪聲對舵機角速率的需求分析

導彈高度10 km，導彈速度3 M，接近速度1 200 m/s，有效導航比取4，噪聲相關時間常數取0.01 s，引入視線角噪聲，噪聲均方根分別取0.5 mrad、1 mrad 和2 mrad(對應的像素數分別為1、2 和4)。仿真結果如圖3 所示，可知，當視線角噪聲為0. 5 mrad(1 個像素)時，需求的舵機角速率為55°/s。

2.2 閃爍噪聲對舵機角速率的需求分析

2.2.1 閃爍噪聲為白噪聲

導彈高度10 km，導彈速度3 M，接近速度1 200 m/s，有效導航比取4，模型中引入閃爍噪聲，噪聲的均方根分別取0.5 m、1 m 及1.5 m，噪聲相關時間常數取0.1 s，仿真結果如圖4 所示。

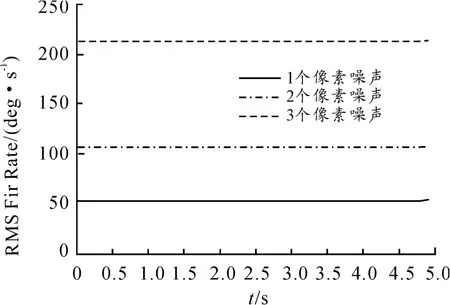
圖3 視線角噪聲對舵機角速率的需求

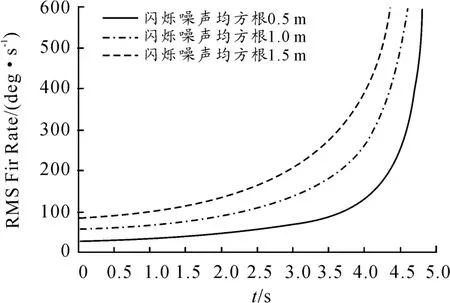
圖4 閃爍噪聲(白噪聲)對舵偏角速率的需求

由圖3 可知，舵機角速率隨著噪聲均方根的增大而增大，彈道末端，需求的舵機角速率增大。當噪聲均方根為0.5 m 時，在彈道結束前0.3s 所需的舵機角速率達到380°/s。

2.2.2 閃爍噪聲為隨機噪聲

對紅外導引頭而言，閃爍噪聲一般為跟蹤點跳動。由于閃爍噪聲具有低頻、自相關的特性，其帶寬與系統帶寬接近，一般不把閃爍噪聲近似為白噪聲。可利用白噪聲通過一個成形濾波器來等效閃爍噪聲

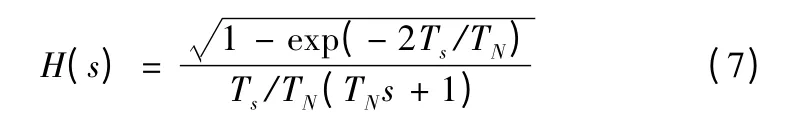
式中:Ts為系統采樣周期;TN為成形濾波器時間常數。

由隨機過程可知，若白噪聲通過的成形濾波器的傳遞函數為

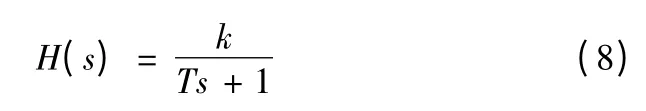
則輸入白噪聲的功率譜密度為

其中:T 為濾波器時間常數;σ 為等效的隨機噪聲的均方根。因此在伴隨模型中引入成形濾波器，輸入白噪聲的功率譜密度如下

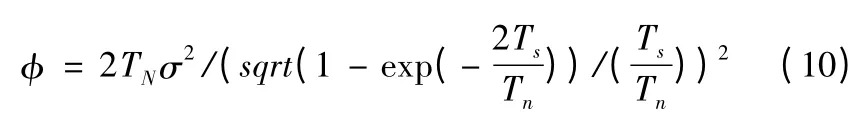
假定閃爍噪聲為隨機噪聲，采用白噪聲通過成形濾波器的方法來生成閃爍噪聲，成形濾波器的傳遞函數見式(8)，白噪聲的功率譜密度按式(9)進行計算，系統的伴隨模型如圖5 所示。

采用上述伴隨模型進行仿真分析，其中導彈高度10 km，導彈速度3M，接近速度1 200 m/s，有效導航比取4，模型中引入閃爍噪聲，噪聲的均方根分別取0.5 m、1 m 及1.5 m，噪聲相關時間常數取0.1 s，仿真結果如圖6 所示。

由圖6 可知，對于特性為隨機噪聲的閃爍噪聲，當噪聲均方根為1 m 時，在彈道結束前0.3 s 時需求的舵機角速率為160°/s 。閃爍噪聲對舵機角速率的需求如表1 所示。

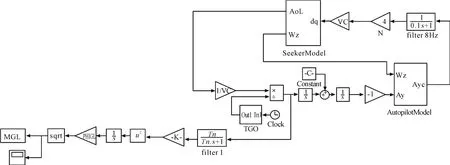
圖5 系統伴隨模型

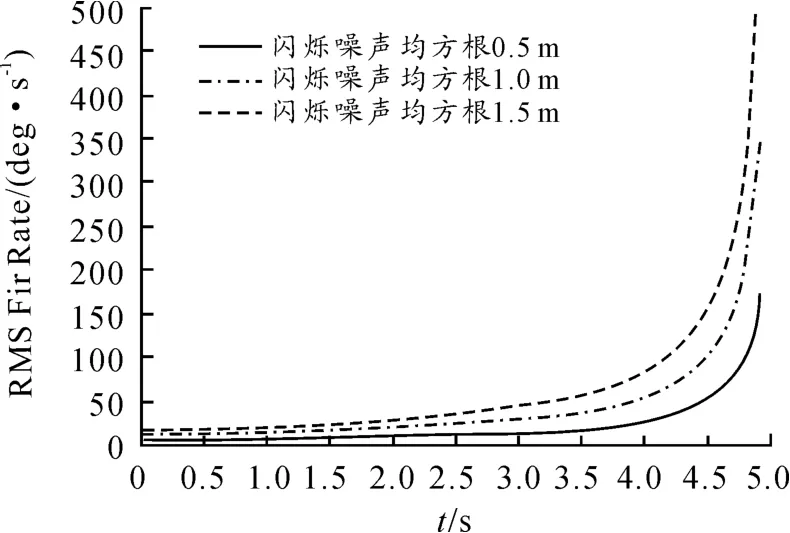
圖6 閃爍噪聲(隨機噪聲)對舵偏角速率的需求仿真結果

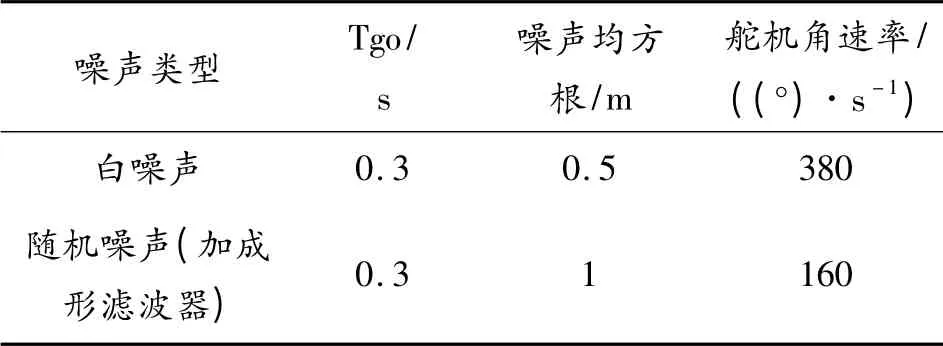
表1 閃爍噪聲需求的舵機角速率

2.3 目標機動對舵機角速率的需求

假設目標做6g 的均勻分布機動，需求的舵機角速率的均方根如圖7 所示。

由圖7 可知，目標機動對舵機角速率的需求很小，可忽略。

3 結論

目標機動對舵機角速率的需求很小，可忽略;

當視線角噪聲為0.5 mrad(1 個像素)時，需求的舵機角速率為55°/s;

閃爍噪聲對舵機角速率需求較大:當閃爍噪聲為隨機噪聲時，噪聲均方根在1 m 左右時，在彈道結束前0.3s 時所需的舵機角速率達到160°/s。

圖7 目標機動對舵偏角速率的需求

綜上可知，當視線角噪聲在0.5 mrad、閃爍噪聲為隨機噪聲且均方根在1 m 左右時，需求的舵機角速率不小于170°/s。

［1］林曉輝，崔乃剛，劉撴.伴隨理論及其在仿真中的應用研究［J］.航天控制，1996(3):1-66.

［2］Paul Zarchan.Complete statistical analysis of nonlinear missile guidance systems-SLAM［Z］.AIAA，77-1094.

［3］Paul Zarchan.Tactical and Strategic Missile Guidance［M］.Fifth Edition.2006.