向量函數微分的非標準定義
陳東立,史艷維,董歡歡
(1.西安建筑科技大學理學院,陜西西安710055;2.西安培華學院基礎部,陜西西安710125)
向量函數微分的非標準定義
陳東立1,史艷維2,董歡歡1
(1.西安建筑科技大學理學院,陜西西安710055;2.西安培華學院基礎部,陜西西安710125)
用非標準分析方法,在擴大模型中使用轉換原理,通過定義局部線性函數,給出向量函數微分的定義.得到了向量函數微分的非標準定義與在一般意義下的定義是一致的結論,并且在此基礎上,給出向量函數在一點處可微的定義.
向量函數;局部線性映射;微分;雅克比矩陣
非標準分析是數理邏輯的一個分支,它引入了超實數,讓“真正的無窮小”存在,這些數字都比小,但比0大.A.Robinson于20世紀60年代創立了非標準分析,非標準分析理論因其自身的優勢已經得到深入研究,并已廣泛應用于巴拿赫空間[1]、微分方程、概率論[2]、數理經濟學[3]、數學物理方程與拓撲學[4]等眾多領域.
本文用非標準分析的方法給出向量函數微分的新定義,從而為向量函數微分的研究提供一種新的途徑.
1 預備知識
設X是一個無限集合,U是標準全域,*U是U的擴大,X包含在標準全域U的個體集中,于是有X?*X(見文獻[5]).
設Rn為實數域R上的n維線性空間,*Rn為Rn的擴大,In為*Rn的無窮小量之集.我們可以得到明顯的封閉性:
引理1[6](1)若x,y∈In,則x+y∈In;(2)如果x∈In,且α∈*R是有限的,則αx∈In.
定義1 設f是一個定義域和值域分別在*Rn和*Rm的子集上的內映射.如果f[In]?Im,則f被稱做局部映射.
定義2 局部映射被稱做局部線性的.如果滿足:
(1)若x,y∈In,則f(x+y)=f(x)+f(y);
(2)如果x∈In,并且α∈*R是有限的,則f(αx)=αf(x).
定義3 設f,g是從In到Im的兩個映射,如果對一切的h∈In,h≠0,f,g滿足

則稱f和g等價,并且記作f~g.
引理2[6](轉換原理) 設α是L的一個句子,則*|=*α當且僅當|=α.
引理3[6]設f是從Rn到Rm的映射,則f在x0∈Rn處是連續的,當且僅當對于一切x∈*Rn,x≈x0蘊涵f(x)≈f(x0)恒成立.
2 向量函數微分的非標準定義
定理1 設f是局部線性的,則存在一個唯一的*Rn到*Rm的內部線性算子,使得對于一切x∈In,f(x)=Tx,而且‖T‖是有限的.
證明 設α,β為*R中的無窮小非零元,令x∈*Rn使得αx,βx≈0,則

設ν為某固定的無限整數,則對一切非零的x∈*Rn,且x≠0,有成立.定義
其中x≠0,T0=0.
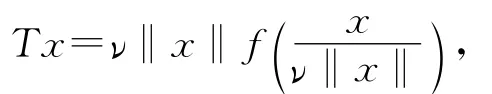
因此,‖T‖是內的.而且,對于每個無窮小量α使得αx≈0,由(1)式得特別地,如果x∈In,對任意的α≈0,我們有,
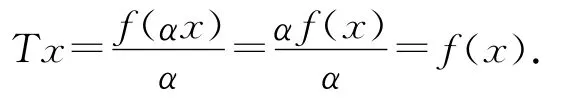
接下來,我們驗證T是線性的.設x,y∈*Rn,且選取α∈*R,使得α≈0,αx,αy≈0,則
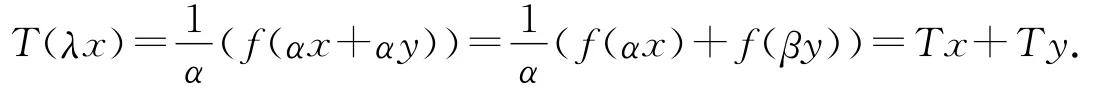
為了驗證唯一性,對x∈In,設f(x)=T1x=T2x,其中T1,T2是*Rn上的線性算子.對任意的x∈*Rn,

最后,假設‖T‖是無限的,則由轉換原理,對某個x∈*Rn且‖x‖=1,有‖Tx‖≥‖T‖-1,即‖Tx‖必須是無限的,從而

則
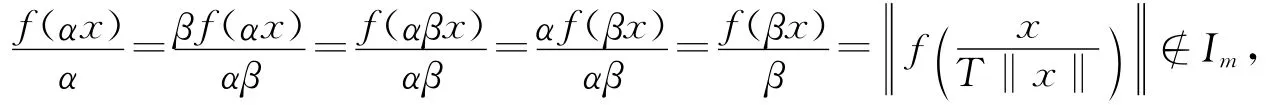
矛盾.
定理2 設f1,f2為局部線性映射,且設T1,T2是由定理1得到的分別關于f1,f2的內線性算子,則f1~f2,當且僅當對于所有的x∈*Rn,且‖x‖=1,T1x≈T2x成立.
證明 首先對于x∈*Rn且‖x‖=1,設T1x≈T2x,再設u∈In,則
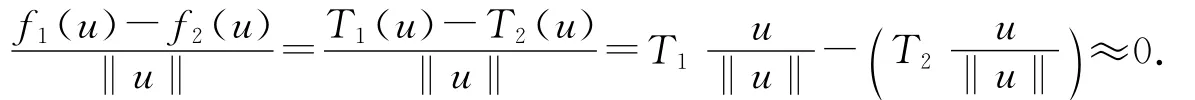
故f1~f2.
反之,如果f1~f2,且‖x‖=1,則選取α≈0,且α>0,從而有
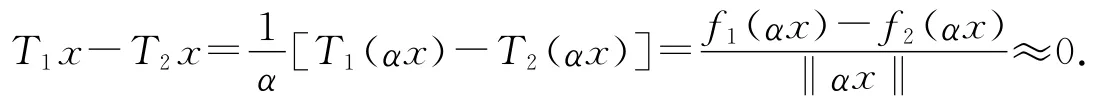
定義4 局部線性映射f被稱做微分,如果存在一個有界線性變換T:Rn→Rm,使得對一切x∈In,有Tx=f(x).
定理3 如果f1,f2是兩個微分,且f1~f2,則f1=f2.
證明 我們有標準的線性算子T1,T2,使得對于所有x≈0,有f1(x)=T1x,f2=T2x.由定理2對‖u‖=1,且T1u≈T2u.對Rn中的標準點u滿足‖u‖=1,便有T1u=T2u.故對任何的x∈Rn,如果x≠0,

最后,因為T1=T2,所以就有f1=f2.
定義5 設任意的映射f:Rn→Rm,且設x0∈Rn,則把由Δx0f(u)=f(x0+u)-f(x0)定義的In上的映射記為Δx0f.
推論1 f在點x0是連續的當且僅當Δx0f是局部映射.
定義6 設映射f:Rn→Rm,且設x0∈Rn.如果Δx0f等價于一個微分,則稱f在點x0是可微的.
設f為一個從Rn到Rm的任意映射,則存在一個Rn到Rm上的線性變換A,使得對x=(x1,…,xn)T∈Rn,f(x)=Ax.設f在點x0是連續的,則對所有的u=(u1,u2,…,un)T∈In,Δx0f是局部線性映射,并且有Δx0f(u)=f(x0+u)-f(x0)=A(x0+u)-A(x0)=A(x0)+A(u)-A(x0)=A(u).
由定義4,我們只需檢驗A是有界的,使得Δx0f(u)是一個微分.顯然,A是有界的,否則,Δx0f(u)=A(u)將不是局部線性映射,矛盾.設A為線性變換A的關系矩陣.由定理3,存在唯一一個微分與Δx0f等價.我們記為dx0f或df,且有dx0f(u)=A(u)或df(u)=A(u),即

其中對u=(u1,u2,…,un)T≈0,α(u)≈0(換言之,α是局部映射).
現在,我們可以發現,這種用非標準分析方法定義的向量函數微分與向量函數微分的一般定義是一致的,其中關系矩陣A稱為f在點x0處的導數矩陣,有時也被稱為f的雅克比矩陣.
例1 設n=m=1,且f(x)=x2,則Δx0f(x)=(x0+dx)2-x02=2x0dx+dx2.因為dx2是比dx高階的無窮小量,即

[1] HENSONC W,MOORE L C.Nonstandard analysis and the theory of Banach space in nonstandard analysis-recent development[J].Lecture Notes in Athematics,1983,983:27-112.
[2] LOEB P A.Conversion from nonstandard measure space and application to probability theory[J].Trans Math Soc,1975,211:113-122.
[3] 韓俊峰,韓偉.非標準分析在經濟學中的應用[J].西安財經學院學報,2005,18(2):12-15.
[4] ALBEVERIO S,FENSTAD J E.Nonstandard methods in Stochastic analysis and athematical physics[M].New York:Academic Press,1986:36-43.
[5] 陳東立,馬春暉,史艷維.拓撲的非標準定義[J].西北大學學報:自然科學版,2006,36(3):348-350.
[6] DAVIS M.Applied nonstandard analysis[M].New York:Wiley,1977:55-78.
Nonstandard definition of differential of vector function
CHEN Dong-li1,SHI Yan-wei2,DONG Huan-huan1
(1.School of Science,Xi'an University of Architecture and Technology,Xi'an 710055,China;2.Department of Basic Courses,Xi'an Peihua University,Xi'an 710125,China)
To define the differential of vector function by nonstandard analysis method.In the enlarged model,by transfer principle,the differential of vector function is defined with locally linear map.The nonstandard definition of differential of vector function is consistent with the general,and based on it,the definition of differentiable of vector function at a point is shown.
vector function;locally linear map;differential;Jacobian matrix
O 141.41 [學科代碼] 110·37
A
(責任編輯:陶 理)
1000-1832(2015)03-0037-03
10.16163/j.cnki.22-1123/n.2015.03.008
2013-12-23
陜西省自然科學基金資助項目(2007A12);陜西省教育廳專項科研基金資助項目(2013JK0574);西安建筑科技大學人才科技基金資助項目(RC1239);西安培華學院科研項目(PHKT20130609).
陳東立(1963—),男,教授,主要從事非標準分析理論研究.

