一類分?jǐn)?shù)階脈沖微分方程邊值問題的多重正解
張愛華,胡衛(wèi)敏
(1.伊犁師范學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,新疆伊寧835000;2.菏澤市第二中學(xué),山東菏澤274000)
一類分?jǐn)?shù)階脈沖微分方程邊值問題的多重正解
張愛華1,2,胡衛(wèi)敏1
(1.伊犁師范學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,新疆伊寧835000;2.菏澤市第二中學(xué),山東菏澤274000)
通過錐拉伸與錐壓縮不動(dòng)點(diǎn)定理得到了一類非線性分?jǐn)?shù)階脈沖微分方程邊值問題正解的存在性和多重性結(jié)果.
脈沖微分方程;邊值問題;分?jǐn)?shù)階導(dǎo)數(shù);錐拉伸與錐壓縮不動(dòng)點(diǎn)定理
0 引言
非線性脈沖微分方程是描述狀態(tài)在某些時(shí)刻發(fā)生瞬間突變的過程,因其能更深刻、精確地反映事物的變化規(guī)律,日益引起人們的重視,使它在物理、經(jīng)濟(jì)、生命科學(xué)、醫(yī)學(xué)、航天技術(shù)、工程技術(shù)、人口動(dòng)態(tài)分布等領(lǐng)域都有廣泛的應(yīng)用[1-2].隨著脈沖微分方程理論的發(fā)展,人們開始關(guān)注脈沖微分方程邊值問題的研究.關(guān)于整數(shù)階脈沖微分方程兩點(diǎn)、三點(diǎn)和多點(diǎn)邊值問題解的存在性和唯一性的研究已經(jīng)取得了一定的成果[3-5],但是很少有文獻(xiàn)研究非線性分?jǐn)?shù)階脈沖微分方程邊值問題解的存在性[6-12].
本文運(yùn)用錐拉伸與錐壓縮不動(dòng)點(diǎn)定理給出如下分?jǐn)?shù)階脈沖邊值問題:
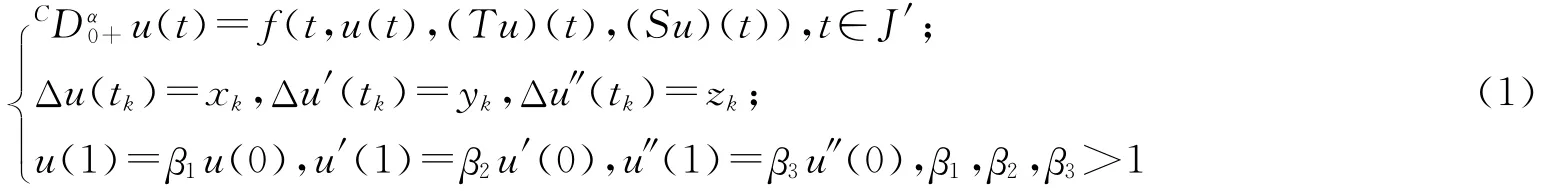
正解的存在性和多重性.其中:2<α≤3;CDα0+是Caputo分?jǐn)?shù)階導(dǎo)數(shù);R+=[0,∞);f∈C([0,1]×R+× R+×R+,R+);xk,yk,zk∈C(R+,R+);J=[0,1],J′=J\{t1,t2,…,tm},k=1,2,…,m;J0=[0,t1],Jk=(tk,tk+1],0=t0<t1<…<tm<tm+1=1;Δu(tk)=u(t+k)-u(t-k),u(t+k)與u(t-k)分別表示u(t)在tk處的右極限與左極限,且u(t-k)=u(tk),Δu′(tk)和Δu″(tk)對u′(t)和u″(t)也有類似定義.此外
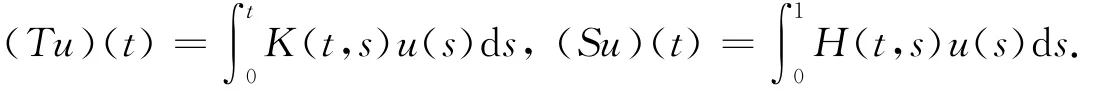
K∈C(D,R+),D={(t,s)∈J×J|t≥s},H∈C(J×J,R+).
定義PC(J,R)={u:J→R|u∈C(Jk),k=0,1,2,…,m;u(t+k)存在,k=1,2,…,m},則PC(J,R)是以為范數(shù)的Banach空間.
若u∈PC2(J,R)∩AC3(J′,R)滿足(1),并且u(t)>0,t∈J,則稱u為問題(1)的正解.
1 預(yù)備知識(shí)
首先,我們給出一些分?jǐn)?shù)階微積分理論的定義和定理,參見文獻(xiàn)[12-16].定義1.1[13]函數(shù)f:[0,∞)→R的α>0階Riemann-Liouville積分是指
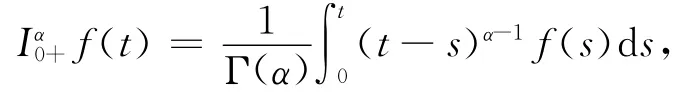
其中右邊是在[0,∞)上逐點(diǎn)定義的.
定義1.2[14]函數(shù)f:[0,∞)→R的α>0階Riemann-Liouville微分是指
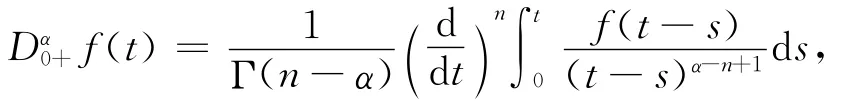
其中n=[α]+1,右邊是在[0,∞)上逐點(diǎn)定義的.特別地,當(dāng)α=n時(shí),Dn0+f(t)=f(n)(t).
定義1.3[15]函數(shù)f:[0,∞)→R的α>0階Caputo微分是指
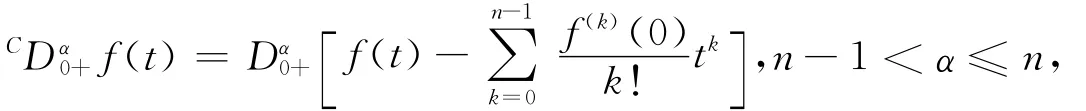
其中右邊是在[0,∞)上逐點(diǎn)定義的.特別地,當(dāng)α=n時(shí),CDn0+f(t)=f(n)(t).
引理1.1[15]設(shè)n-1<α≤n,f(t)∈Cn([0,∞),R),則:
引理1.2[12]令0<α<1,h∈C([0,T],R),函數(shù)x∈C([0,T],R)是分?jǐn)?shù)階邊值問題

的解當(dāng)且僅當(dāng)x是如下積分方程的解:
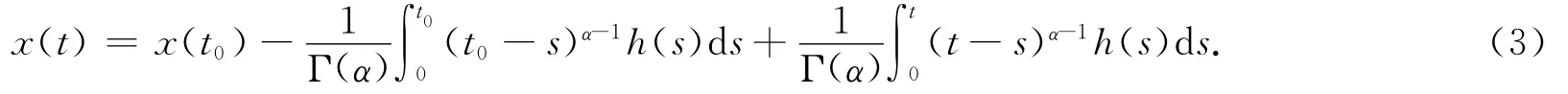
引理1.3[16]令X是一個(gè)Banach空間,P?X是X中的一個(gè)錐.假設(shè)Ω1,Ω2?P為非空相對開集,且0∈Ω1?ˉΩ1?Ω2,設(shè)T:P→P為全連續(xù)算子,滿足下列條件之一:
(ⅰ)‖Tx‖≤‖x‖,x∈P∩?Ω1,且‖Tx‖≥‖x‖,x∈P∩?Ω2;
(ⅱ)‖Tx‖≥‖x‖,x∈P∩?Ω1,且‖Tx‖≤‖x‖,x∈P∩?Ω2.
則T在P∩(ˉΩ2\Ω1)中有不動(dòng)點(diǎn).
引理1.4 令2<α≤3,假設(shè)h:[0,1]→R+是一個(gè)連續(xù)函數(shù),則邊值問題
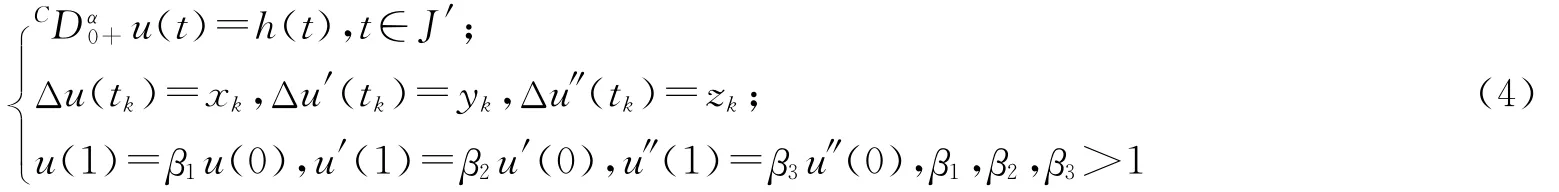
等價(jià)于積分方程
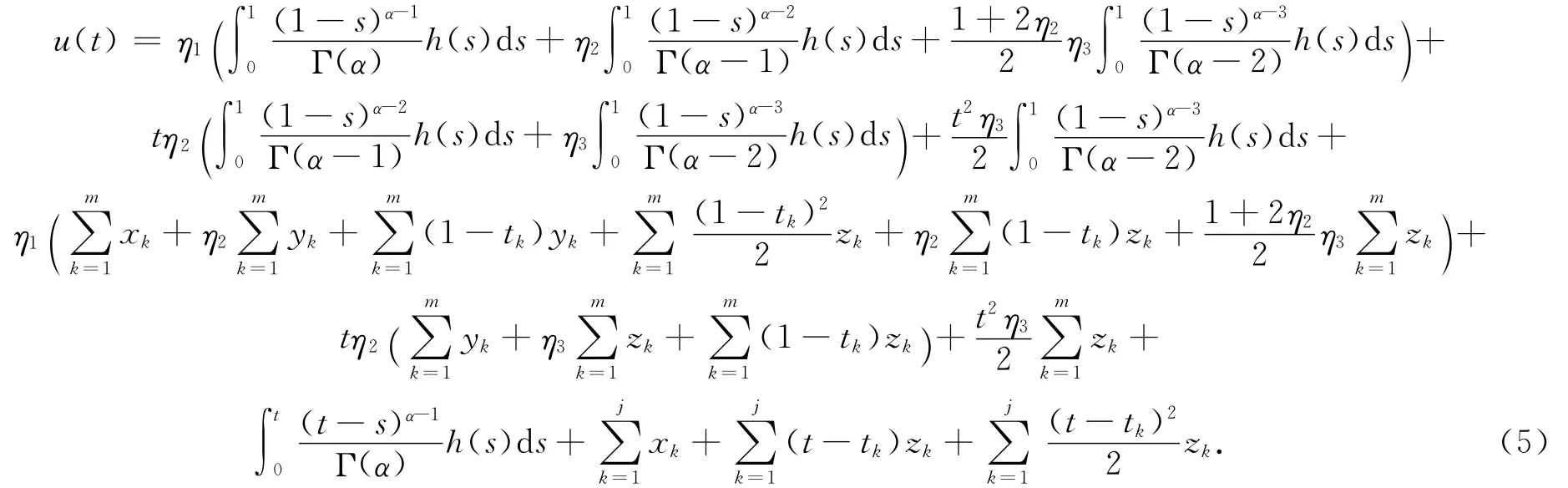
證明 令u(t)是問題(4)的解,利用引理1.1的(1),當(dāng)t∈[0,t1]時(shí),有
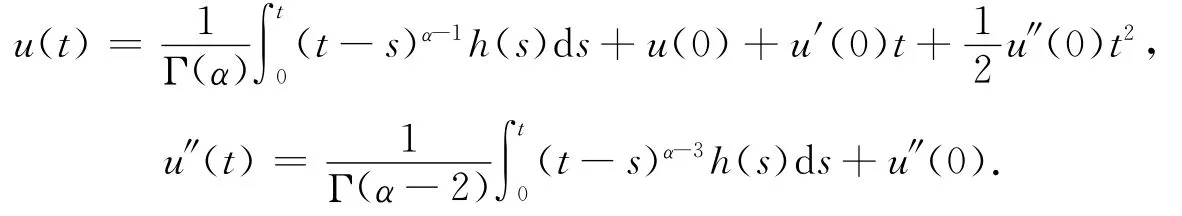
當(dāng)t∈(t1,t2]時(shí),由引理1.2及注1.1可得
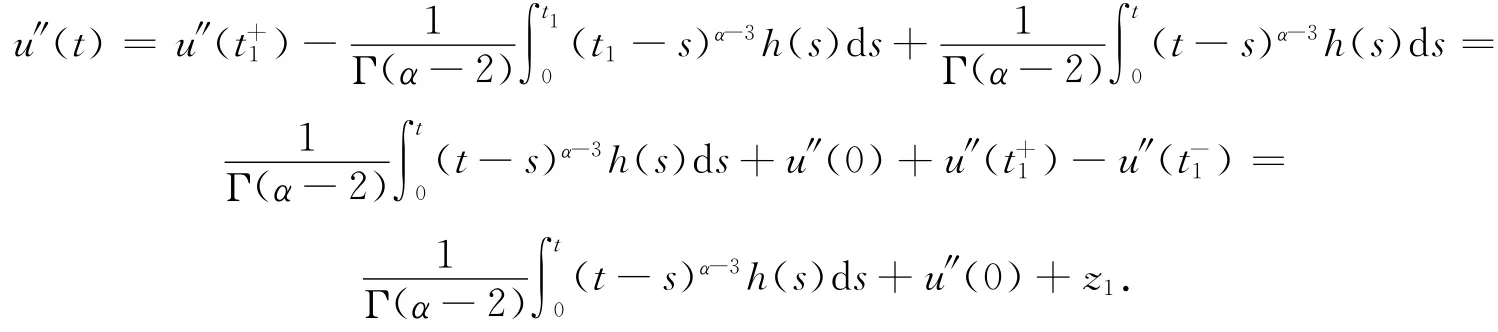
同理,當(dāng)t∈(tj,tj+1]時(shí),有
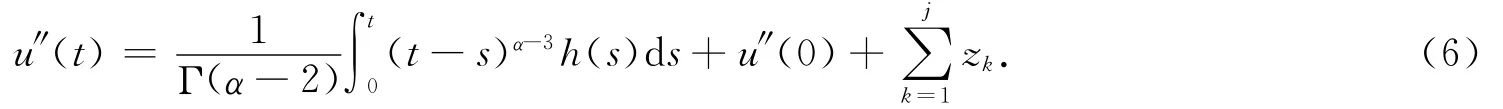
對(6)式從0到t進(jìn)行2次積分,得
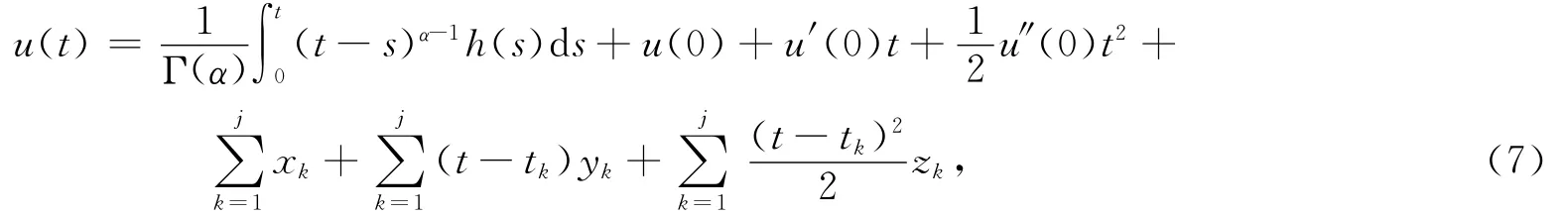
則

代入邊界條件u(1)=β1u(0),u′(1)=β2u′(0),u″(1)=β3u″(0),有
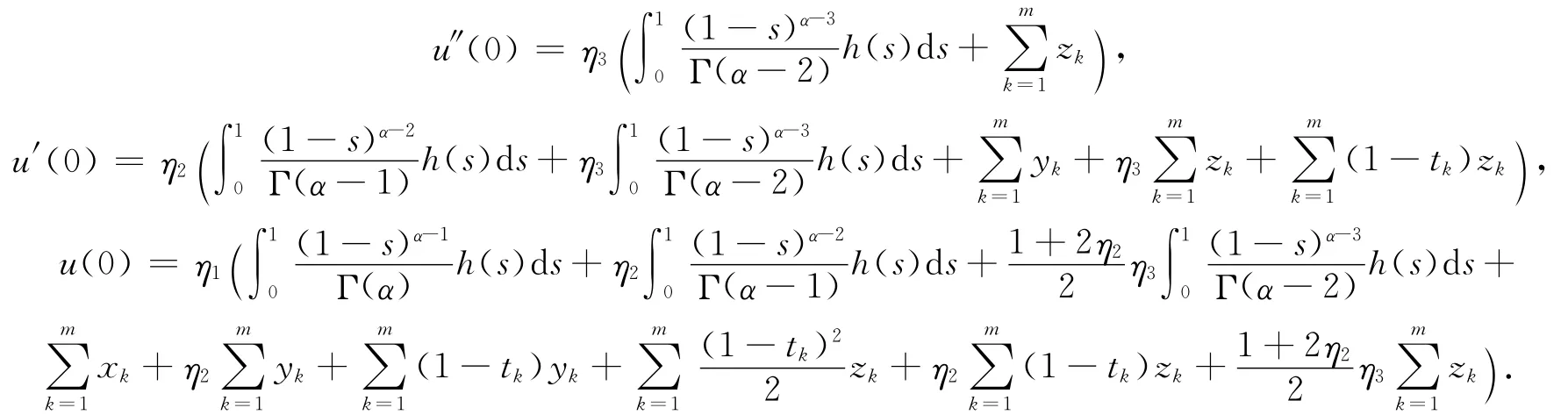
代入(7)式,得(5)式成立.
相反,若u(t)是方程(5)的解,由引理1.1的(2)和Caputo導(dǎo)數(shù)的定義可得u(t)是(4)式的解,證畢.
記σ(t)∶=f(t,u(t),(Tu)(t),(Su)(t)),由引理1.4可知邊值問題(1)有解,等價(jià)于如下定義的積分算子F:PC(J,R)→PC(J,R)有不動(dòng)點(diǎn).
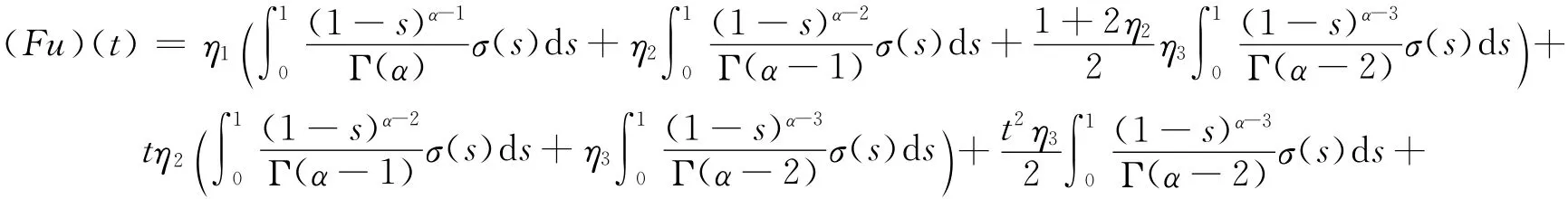
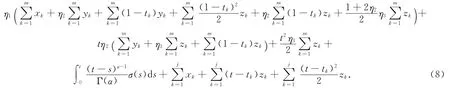
2 主要結(jié)論
為證明正解的存在性,現(xiàn)作如下假設(shè):
(H1)存在常數(shù)k*,h*>0,使得
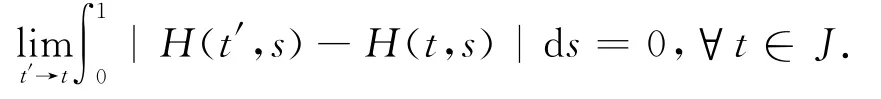
(H2)當(dāng)u→∞時(shí)對t∈J一致成立.
(H3)當(dāng)u→0+時(shí)對t∈J一致成立.
(H4)當(dāng)u→0+時(shí)0,k=1,2,…,m.
(H5)對任意t∈J,存在非負(fù)連續(xù)函數(shù)a(t),ɡ(u,v,w),使得
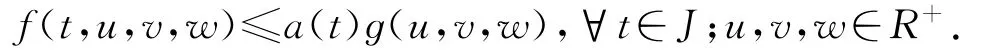
引理2.1 若條件(H1)成立,則F:Q→Q是全連續(xù)的.
證明 首先,由函數(shù)f,xk,yk,zk的連續(xù)性以及Lebesgue控制收斂定理,易知算子F也是連續(xù)的.往證F:Q→Q.事實(shí)上,對任意u∈Q,存在r1≥‖u‖,
記
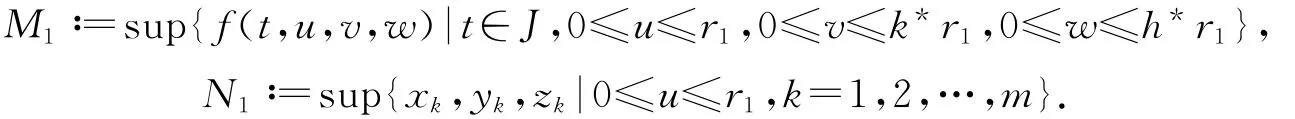
則

則
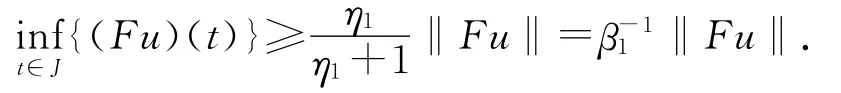
故Fu∈Q.從而F:Q→Q.
再證F映有界集為有界集.只需證明對任意u∈Q,存在常數(shù)l>0,使得‖F(xiàn)u‖≤l,由以上證明過程可知,取l=(η1+1)(aM1+bN1)即可.
最后證F映有界集為Q中等度連續(xù)集.對任意tk<t<t′≤tk+1;k=0,1,2,…,m;u∈Q.有

由于當(dāng)t′→t時(shí),上述不等式右端趨于0,故F在每個(gè)區(qū)間Jk上等度連續(xù).由廣義的Arzela-Ascoli定理可知F是全連續(xù)算子.
定理2.1 若條件(H1),(H2),(H3)成立,并且存在r>0,使得(η1+1)(aMr+bNr)<r,其中
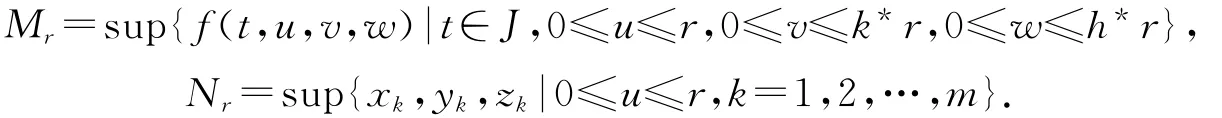
則邊值問題(1)至少有兩個(gè)正解u1和u2,滿足

證明 由引理2.1知,(8)式所定義的算子F:Q→Q是全連續(xù)的.下面需要證明F在Q中有兩個(gè)不動(dòng)點(diǎn)u1和u2,滿足0<‖u1‖<r<‖u2‖.由條件(H2)知,存在r1>0,使得
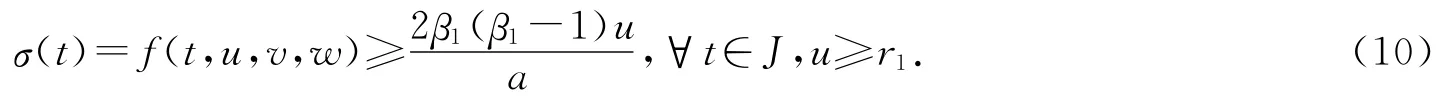
取r2>max{β1r1,r},對任意u∈Q,‖u‖=r2,有

由(10),(11)式及算子F的定義知
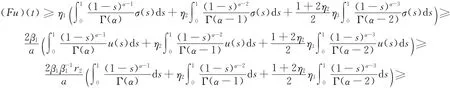

故
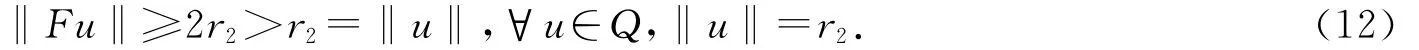
同理,由條件(H3)知,存在r3>0,使得
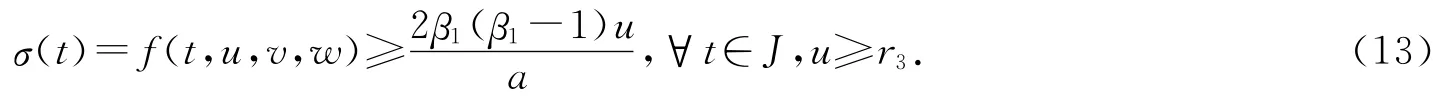
取0<r4<min{r3,r},對任意u∈Q,‖u‖=r4,有
則
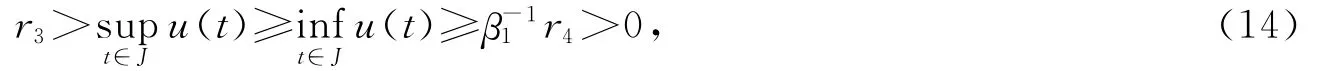
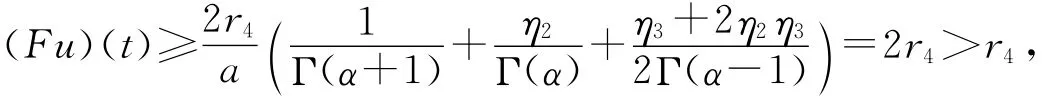
故
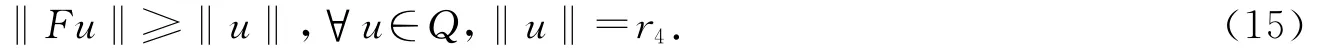
另一方面,對任意u∈Q,‖u‖=r,類似于(9)式有
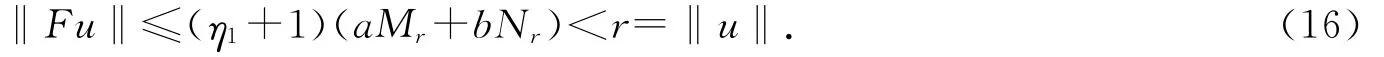
因?yàn)?<r4<r<r2,由(12),(15),(16)式及引理1.3得,F(xiàn)在Q中有兩個(gè)不動(dòng)點(diǎn)u1和u2,滿足
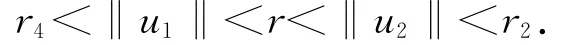
定理2.2 若條件(H1),(H2),(H4),(H5)成立,并且當(dāng)u+v+w→0+時(shí),則邊值問題(1)至少有一個(gè)正解u,滿足
證明 如定理2.1的證明,取r2>β1r1>0,使得
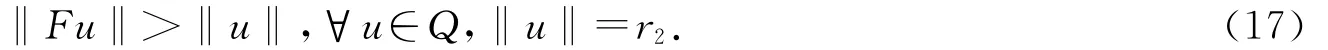
取ε0=[2(η1+1)(a(1+k*+h*)a*+b)]-1,由條件知,存在r5>0,使得
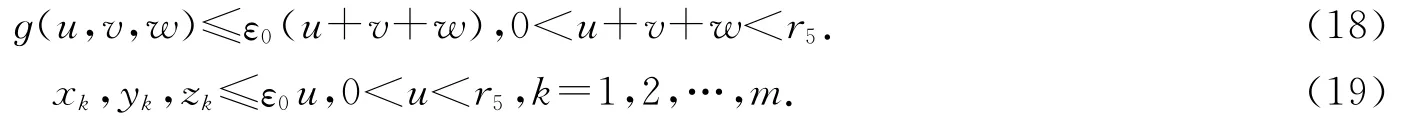
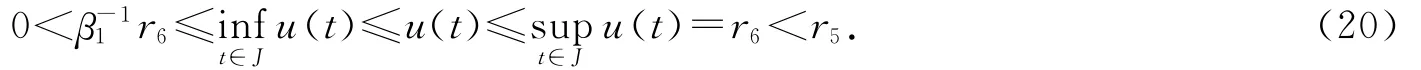
故
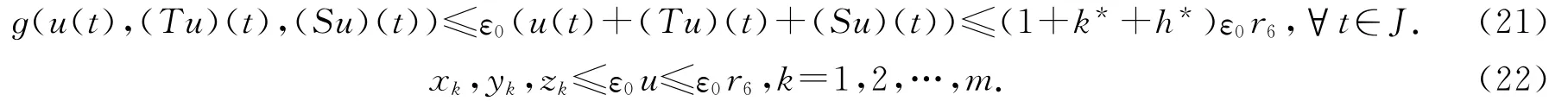
由條件(H5)可得
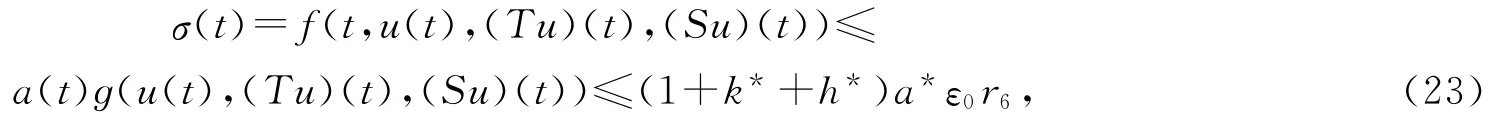
則
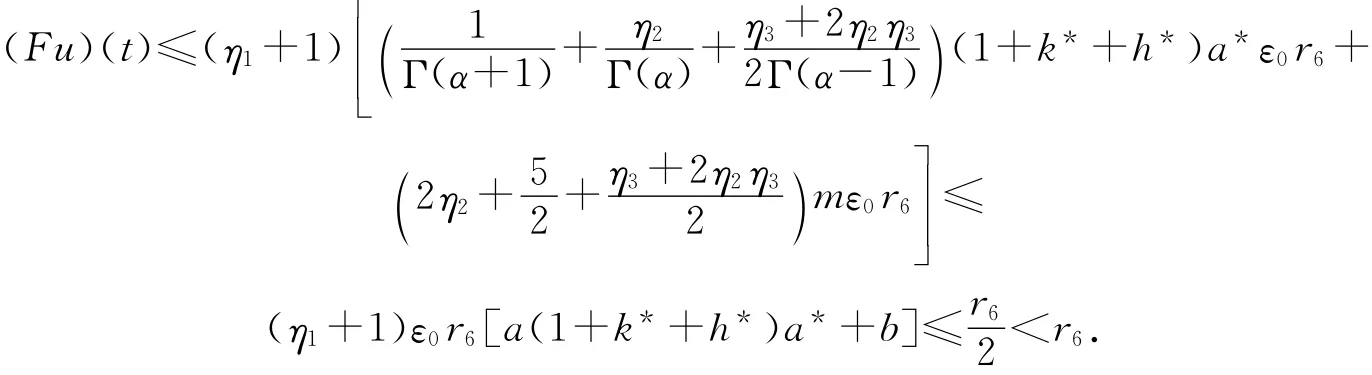
故
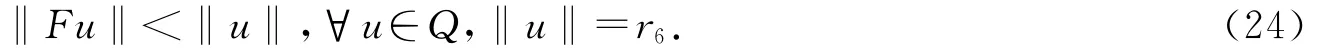
因0<r6<r2,由引理1.3得,算子F在Q中有不動(dòng)點(diǎn)u,滿足r6<‖u‖<r2.
[1] SAMKO S G,KILBAS A A,MARIˇCEV O I.Fractional integrals and derivatives[M].Yverdon:Gordon and Breach Science Publ,1993:366-398.
[2] PODLUBNY I.Fractional differential equations,mathematics in science and engineering[M].New York,London,Toronto:Academic Press,1999:243-313.
[3] DING WEI,WANG YU.New result for a class of impulsive differential equation with integral boundary conditions[J].Commun Nonlinear Sci Numer Simulat,2013,18(5):1095-1105.
[4] GUO DAJUN.Multiple positive solutions for first order impulsive singular integro-differential equations on the half line[J].Acta Mathematica Scientia,2012,32B(6):2176-2190.
[5] WANG XIAOHUAN,ZHANG JIHUI.Impulsive anti-periodic boundary value problem of first-order integro-differential equations[J].Journal of Computational and Applied Mathematics,2010,234(12):3261-3267.
[6] LI XIAOPING,CHEN FULAI,LI XUEZHU.Generalized anti-periodic boundary value problems of impulsive fractional differential equations[J].Commun Nonlinear Sci Numer Simulat,2013,18(1):28-41.
[7] LIU ZHENHAI,LI XIUWEN.Existence and uniqueness of solutions for the nonlinear impulsive fractional differential equations[J].Commun Nonlinear Sci Numer Simulat,2013,18(6):1362-1373.
[8] GUO TIANLIANG,JIANG WEI.Impulsive problems for fractional differential equations with boundary value conditions[J].Computers and Mathematics with Applications,2012,64(10):3281-3291.
[9] AHMAD BASHIR,SIVASUNDARAM S.Existence of solutions for impulsive integral boundary value problems of fractional order[J].Nonlinear Analysis:Hybrid Systems,2010,4:134-141.
[10] WANG GUOTAO,AHMAD BASHIR,ZHANG LIHONG.Impulsive anti-periodic boundary value problem for nonlinear differential equations of fractional order[J].Nonlinear Analysis,2011,74(3):792-804.
[11] CAO JIANXIN,CHEN HAIBO.Impulsive fractional differential equations with nonlinear boundary conditions[J].Mathematical and Computer Modelling,2012,55(3):303-311.
[12] CHEN FULAI.Coincidence degree and fractional boundary value problems with impulses[J].Computers and Mathematics with Applications,2012,64(10):3444-3455.
[13] 許曉婕,胡衛(wèi)敏.一個(gè)新的分?jǐn)?shù)階微分方程邊值問題正解的存在性結(jié)果[J].系統(tǒng)科學(xué)與數(shù)學(xué),2012,32(5):580-590.
[14] 鐘文勇.分?jǐn)?shù)階微分方程多點(diǎn)邊值問題的正解[J].吉首大學(xué)學(xué)報(bào):自然科學(xué)版,2010,31(1):9-12.
[15] KILBAS A A,SRIVASTAVA H M,TRUJILLO J J.Theory and applications of fractional differential equations[M].Amsterda:Elsevier Science B V,2006:59-90.
[16] BAI ZHANBING,LüHAISHEN.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].J Math Anal Appl,2005,311(2):495-505.
Multiple positive solutions for a class of boundary value problem of impulsive fractional differential equations
ZHANG Ai-hua1,2,HU Wei-min1
(1.School of Mathematics and Statistics,Yili Normal University,Yining 835000,China;2.The Second High Middle School of Heze City,Heze 274000,China)
In this paper,we investigate the multiple positive solutions for a boundary value problem of nonlinear impulsive fractional differential equations.The arguments are based upon the fixed point theorem of cone expansion and compression with norm type.
impulsive differential equation;boundary value problem;fractional derivative;fixed point theorem of cone expansion and compression with norm type
O 175.8 [學(xué)科代碼] 110·54
A
(責(zé)任編輯:陶 理)
1000-1832(2015)03-0012-07
10.16163/j.cnki.22-1123/n.2015.03.004
2014-01-10
新疆維吾爾自治區(qū)自然科學(xué)基金資助項(xiàng)目(201318101-14).
張愛華(1984—),女,碩士,主要從事微分方程理論及其應(yīng)用研究;通訊作者:胡衛(wèi)敏(1968—),男,教授,主要從事微分方程理論及其應(yīng)用研究.

