一種動態分組的粒子群優化算法

王燕燕,葛洪偉,王娟娟,楊金龍

(1.江南大學物聯網工程學院,江蘇無錫214122;2.國網濰坊供電公司,山東濰坊261021)

一種動態分組的粒子群優化算法

王燕燕1,葛洪偉1,王娟娟2,楊金龍1

(1.江南大學物聯網工程學院,江蘇無錫214122;2.國網濰坊供電公司,山東濰坊261021)

針對粒子群優化算法易陷入局部最優的問題,提出一種動態分組的粒子群優化算法。通過對鳥群習性的研究,給出交互粒子的概念,并在粒子群優化過程中引入動態分組機制,將種群動態劃分成多個子種群,且每次劃分的子種群數目是從特定集合中隨機選取,從而增加交互粒子劃分到同一子種群的概率。每個子種群在收斂進化的同時,利用環拓撲結構提高種群多樣性及算法搜索全局最優解的能力。實驗結果表明,與其他粒子群優化算法相比,該算法具有更好的穩定性、尋優性能以及更高的收斂精度。

粒子群優化;局部最優;全局最優;交互粒子;動態分組;環拓撲結構

1 概述

粒子群優化(Particle Swarm Optimization,PSO)算法[1]是由Kennedy等人在1995年提出的一種基于種群的智能優化算法,該算法具有可變參數少、簡單易于實現的特點,得到廣泛關注。為了避免粒子陷入局部最優,提高粒子的全局搜索能力,增加算法的應用領域,研究者對其進行了大量研究,以期達到更好的優化能力。在算法參數的改進方面,文獻[2]將慣性權重引入到速度更新公式中,提高了算法的收斂速度;文獻[3-6]研究了慣性權重、參數的設置對算法優化性能的影響。在種群劃分的改進方面,文獻[7]將合作框架引入到PSO算法中,將種群劃分成多個子種群,通過子種群協同合作,提高種群優化性能;文獻[8]將主從模式引入到PSO算法中,將種群劃分成多個子種群:由一個主群和幾個奴仆群組成,提高了種群的多樣性和收斂速度;文獻[9]采用控制理論的分層思想,提出多種群分層PSO算法,有效提高了算法收斂速度;文獻[10]提出一個基于動態鄰居的多子種群PSO算法,避免算法陷入局部最優;文獻[11]在文獻[10]的基礎上,提出一種基于動態鄰居和變異因子思想的粒子群優化算法(DNMSPSO),提升了粒子跳出局部最優的能力。在其他改進方面,文獻[12]提出基于學習策略的綜合學習粒子群優化(CLPSO)算法,提高了算法解決多峰問題的性能;文獻[13]使用Monte Carlo隨機投點的方法確定粒子的具體位置進行協同進化更新,提高了算法優化性能。

上述研究對提升算法的收斂速度和運行效率有一定成效,但在種群多樣性、跳出局部最優及收斂精度上仍存在不足。粒子群優化算法是從鳥群尋找食物的生物現象中得到啟發,鳥群在尋找食物的過程中可能存在結伴現象,且不知道哪幾只鳥結伴和結伴鳥的個數。在粒子群優化算法中,由于粒子之間的“結伴現象”(簡稱交互粒子)事先不知道,交互粒子的個數也不確定,因此交互粒子的出現可能導致種群陷入局部最優。為保證種群的多樣性,避免種群陷入局部最優,提高種群的全局收斂性,提升算法的尋優能力,本文結合鳥群結伴行為的特性,提出一種動態分組的粒子群優化(DGPSO)算法,將種群動態地劃分成多個子種群,每次劃分的子種群數目從特定集合中隨機取得,且子種群的數目不定,從而增加交互粒子劃分到同一子種群的概率,而且在不同子種群中尋找全局最優,能增加種群的多樣性,避免算法易陷入局部最優。

2 標準粒子群

PSO算法是基于社會群體中個體行為的一種群體智能優化算法,它通過共享群體的信息和個體本身經驗的總結來引導個體的行動方向,最終找到問題的最優解。

PSO算法對種群的位置xi=[x1,x2,…,xd]和速度vi=[v1,v2,…,vd],i=1,2,…,N進行隨機初始化,并將通過迭代更新后的xi代入目標函數中,根據適應度值的大小判斷找到粒子群的全局最優解。在迭代過程中,粒子通過2個極值更新其位置和速度。一個極值是粒子本身所遍歷得到的最優解,稱為個體最優解;另一個極值是整個種群到當前時刻所得到的最優解,這個極值稱為全局最優解。此外,還有一個局部最優解,是指從種群中選取一部分作為當前粒子的鄰居,取所有鄰居中適應度值最好的值為當前粒子的局部最優解。PSO算法的速度和位置的更新公式為:

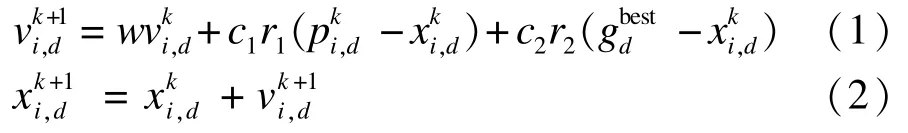
置的d維;w是慣性權重;c1和c2為加速因子,r1和r2是[0,1]內的隨機數。

3 動態分組的粒子群優化算法

3.1 算法原理

優化算法在求解優化問題時,為了簡化問題會在種群的進化開始前就確定好子種群的個數及其各子種群負責搜索的優化范圍[7-11]。然而在優化過程中,給定的子種群粒子之間的關聯不確定,所以這樣一個靜態的分組方法很有可能將交互粒子劃分到不同的子種群中,從而降低粒子的收斂速度,增加粒子陷入局部最優的概率。種群中的交互粒子的數目不確定,可能2個或者更多的粒子是有關聯的,為了便于理解,在此假設種群有2個交互粒子(A和B),且分別被劃分到2個子種群中,迭代過程如圖1所示。

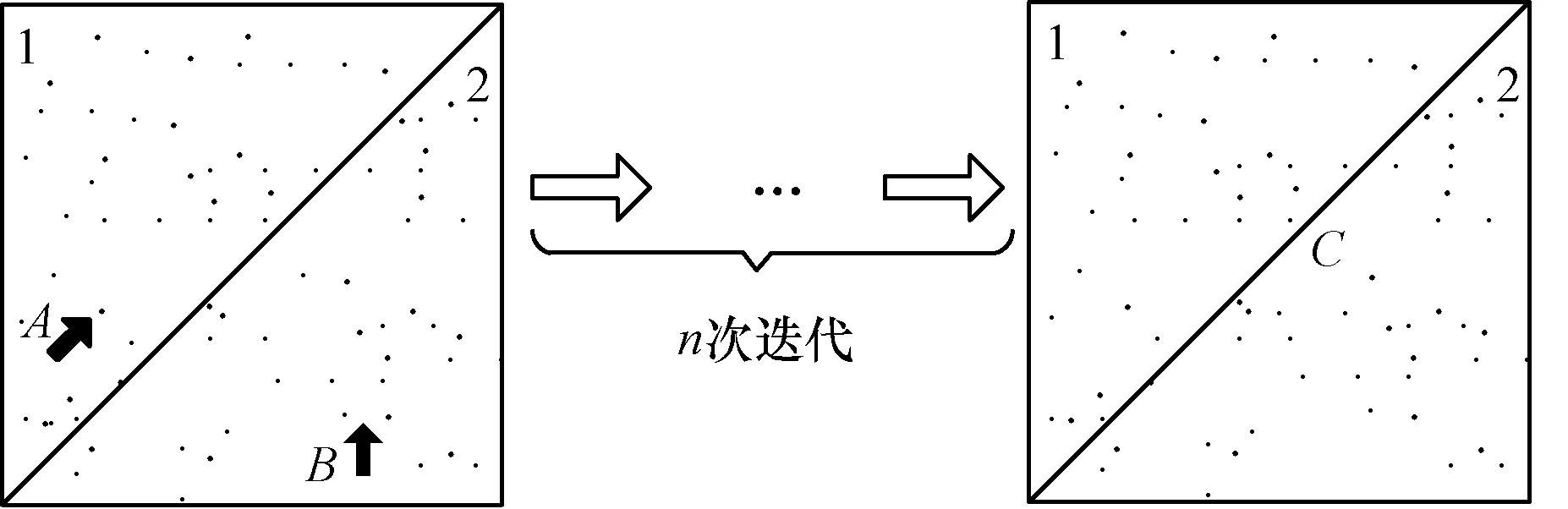
圖1 交互粒子的迭代過程

圖1給出交互粒子的迭代過程,在種群被劃分成2個子種群的情況下進行迭代。其中,黑箭頭表示粒子運動方向;白箭頭表示種群迭代進化的過程;1和2分別表示子種群1和子種群2;A和B分別表示第一次迭代下粒子A和粒子B所處的位置;C表示第n+1次迭代下粒子A和粒子B所處的位置。假設粒子A和粒子B是各自子種群的最優位置。隨著種群的迭代進行,粒子A和粒子B的位置可能更新到同一個位置,那么2個子種群的局部最優解一致,此時,種群極有可能陷入局部最優。

本文在PSO算法思想的基礎上,給出一種具有全局收斂性的改進算法DGPSO。DGPSO算法不指定固定的子種群數目,而是每次迭代時,從集合中隨機選取子種群數目的一種動態的分組方法。這里的集合中包含了幾個可能的從小到大的子種群的數目s,例如,S={2,3,5,6,10}。若適應度得到了改善,則繼續使用原來的s值;否則需要重新選取一個不同的值。盡管仍然需要設置S集,但是參數s不再是必需的。動態隨機分組無需知道待優化問題的任何先驗知識。

3.2 算法進化機制

各子種群分別進行一次優化搜索后,粒子各維的位置改變一次,粒子各維的速度更新公式為:

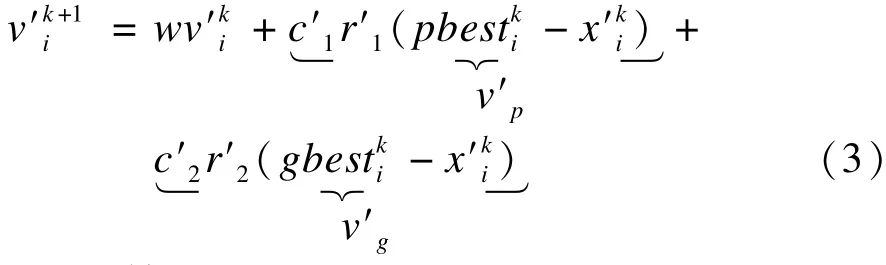
位置更新公式為:

其中,i是第m個子種群內的粒子;m是從集合S=[s1,s2,…,st]中隨機取得的分群數目;v′p是粒子i的認知部分;v′g是粒子i的社會部分;是第k次迭代中粒子i的局部最優解;是當前粒子i對應的全局最優解;和是第k次迭代中粒子i對應的速度和位置;w是慣性權重;c1和c2為加速因子;r1和r2是[0,1]內的隨機數。

在DGPSO算法中,采用環拓撲結構策略求解局部最優解,求解過程如圖2所示。以圖2中粒子A為例,當前的粒子是A時,鄰域為粒子B、粒子H,取3個粒子的適應度最小值作為粒子A的局部最優解;當前的粒子是B時,鄰域為粒子A、粒子C,取3個粒子的適應度最小值作為粒子B的局部最優解;以此向后進行類推;當前的粒子是H時,整個粒子群的環拓撲循環結束。A=min(A,B,H)表示當前的粒子A與鄰域粒子B、粒子H的適應度進行比較,找出適應度值最小值對應的粒子作為該粒子A的局部最優解。

圖2 環拓撲結構

為取得更好的收斂性能,隨著迭代的進行,粒子群的搜索范圍從全局逐步向局部進行搜索,w值也隨之改變,w的更新公式如下[2]:

其中,wmax表示慣性權重的最大值;wmin表示慣性權重的最小值;u表示當前的迭代次數;maxiter表示粒子群優化的最大迭代次數。

3.3 算法步驟

算法步驟具體如下:

步驟1設置粒子群數目、最大迭代次數、慣性權重最大值及最小值、學習因子、狀態值cc和子種群數目集合S。

步驟2隨機初始化種群中粒子的初始位置和速度。

步驟3在約束條件下求出粒子的適應度值,并分別記錄個體最優解和全局最優解。

步驟4判斷狀態值cc是否等于0,若等于0,則從集合S=[s1,s2,…,st]中隨機選取子種群的數目,按照該子種群的數目重新劃分子種群;若不等于0,則子種群保持當前劃分。

步驟5分別求出各子種群的適應度值,記錄個體最優解和各子種群的全局最優解,通過環拓撲結構策略,求出粒子的局部最優解。

步驟6利用式(3)、式(4)更新各子種群中粒子的速度和位置。

步驟7各子種群的全局最優解與粒子群的全局最優解比較,若粒子群的全局最優解并沒有得到更新,則狀態值cc不變;若得到更新,則狀態值cc加1。

步驟8判斷是否滿足終止條件,即是否已經達到設置的最大迭代次數,若滿足,則執行步驟9;否則返回執行步驟4。

步驟9終止優化運算,輸出粒子的最優位置和全局最優解。

3.4 算法驗證

在種群進化迭代中,給定的粒子群數目N隨機分成m個子種群,每個子種群包含個粒子。隨著迭代次數的增加,2個交互粒子被劃分到相同子種群的概率變得更高(推理過程,見證明),概率公式如下:

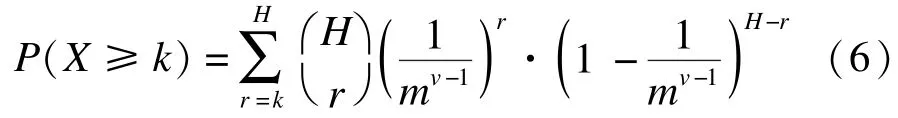
其中,X是交互粒子劃分到同一個子種群的次數;k是交互粒子劃分到同一個子種群的迭代次數;r是當前的迭代次數;H是總的迭代次數;是的簡寫,是從H個次數中取出r(r≤H)次的組合數;m是子種群數目;v是交互粒子的總數;X取大于或等于k值;k值限制在一個小于H大于0的范圍內。

證明:

(1)將種群劃分成m個子種群;

(2)由概率公式可知,在種群中的粒子被劃分到其中一個

(3)假設在種群中存在著v個交互粒子,那么這些交互粒子被劃分到同一個子種群中的概率為:

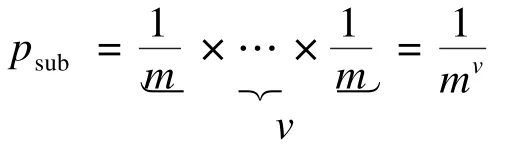
(4)種群中共有m個不同的子種群,所以在種群中與步驟(3)一樣的情況會有m種不同劃分的可能,則總概率為:

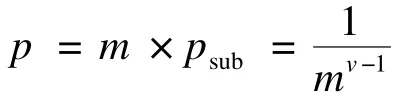
(5)種群在經過r次迭代后,所有N個粒子隨機劃分到m個子種群中,由二項概率分布可知,計算種群中所有交互粒子到同一個子種群的概率公式如下:

由上述證明過程可知,在不同迭代次數下,交互粒子被劃分到相同子種群的概率見式(6)。

實例當N=40,m=10,H=50,v=4時,交互粒子劃分到同一個子種群的概率為:

其中,p(1)表示在50次迭代中2個粒子被放置到同一個子種群中的情況出現一次的概率;p(2)表示在50次迭代中2個粒子被放置到同一個子種群中的情況出現2次的概率;p(50)表示有50個這樣的情況“成功”的概率。式(7)表明,隨機分組策略將幫助解決交互粒子的問題,且概率會隨著子種群的數目變化而發生相應改變。種群最優解的更新如圖3所示。

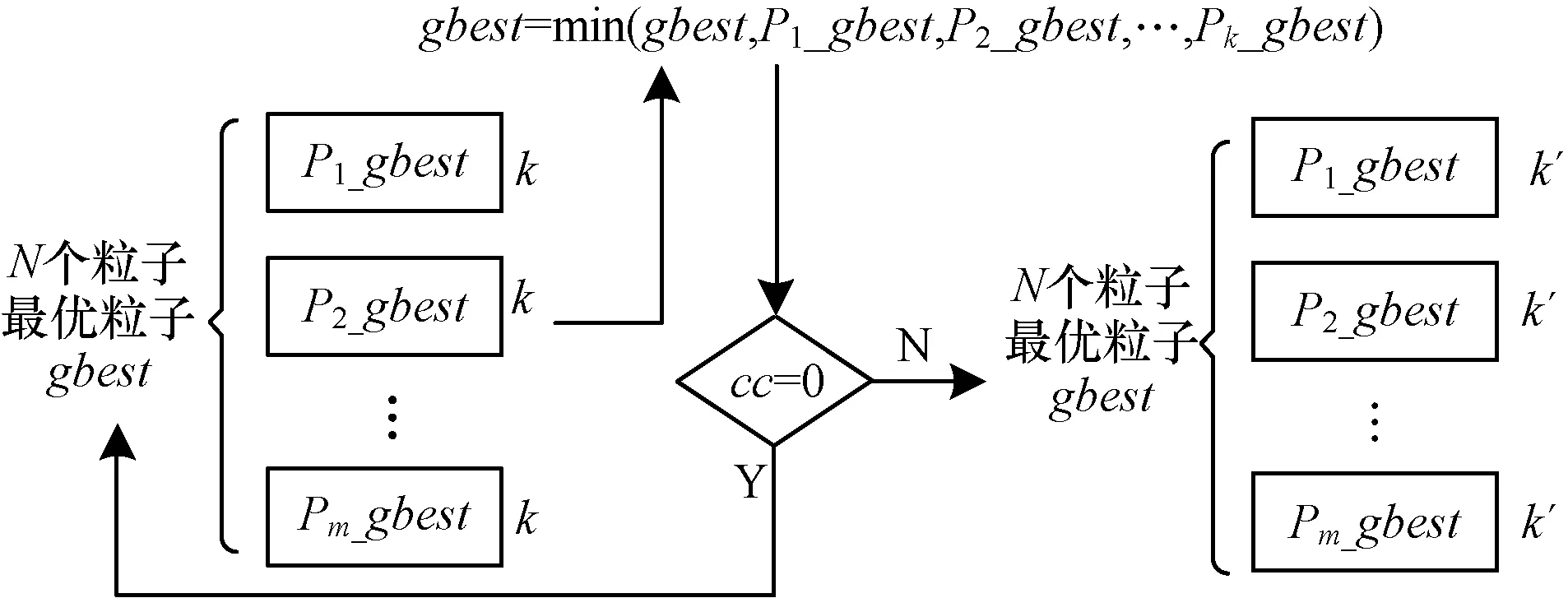
圖3 種群最優解更新

將每個子種群的全局最優解Pi_gbest,i=1, 2,…,m分別與種群的全局最優解gbest進行比較,用最小值取代gbest(gbest=min(gbest,P1_gbest,P2_gbest,…,Pk_gbest)),若gbest得到更新,那么仍繼續使用現在的分組進行迭代;若gbest沒有得到更新,則需要對種群進行重新分組。其中,k,k′表示粒子數;m表示子種群數目。

4 實驗結果與分析

4.1 測試函數

為測試本文算法性能,采用了12個測試函數。

其中,f1～f5函數是單峰函數;f6～f12函數是多峰函數。函數具體取值范圍和最優解如表1所示。

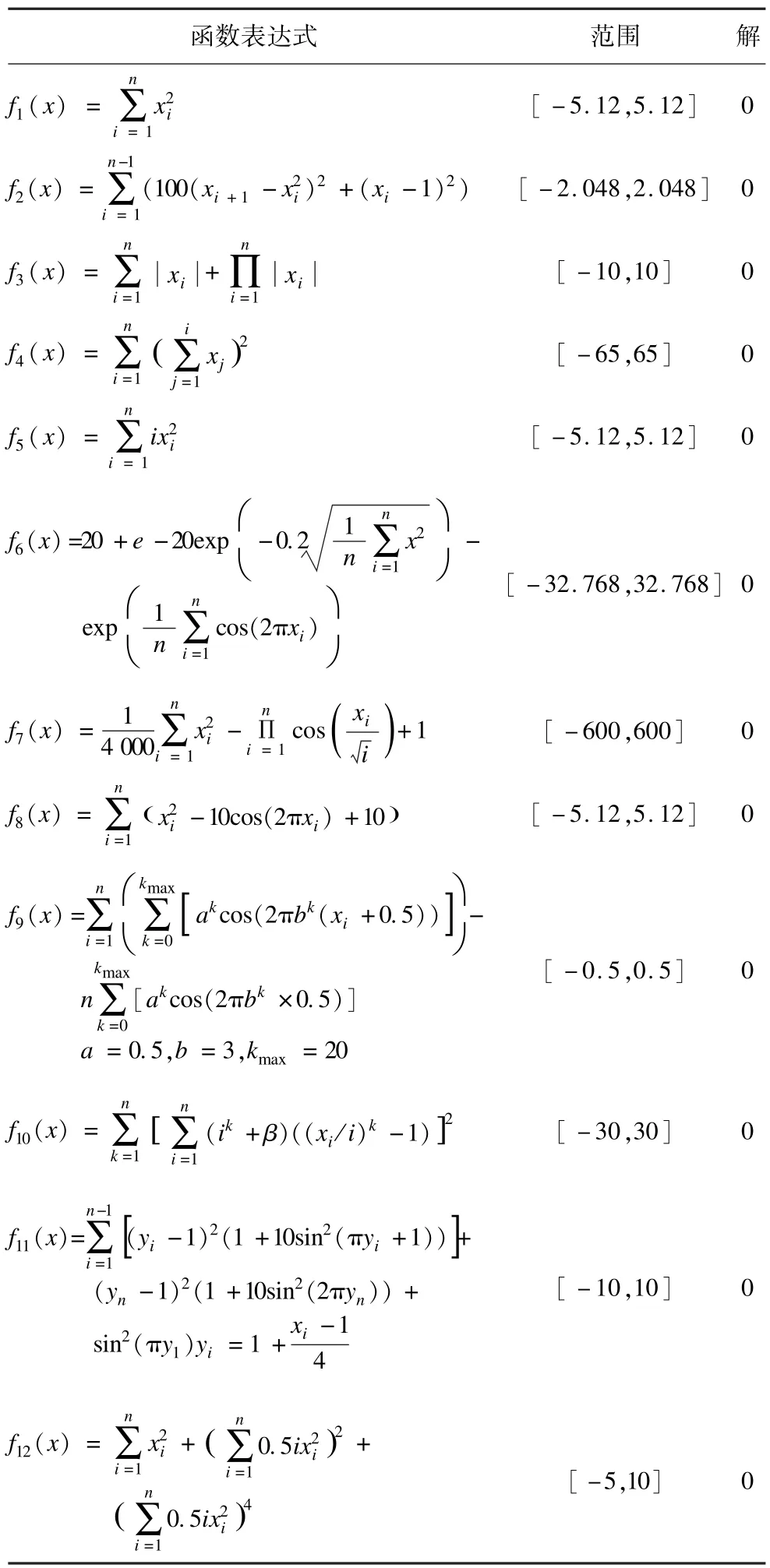
表1 測試函數

4.2 結果分析

為測試DGPSO算法的有效性,本文將DGPSO算法與以下算法進行對比:

(1)基本粒子群優化算法PSO[2];

(2)基于動態鄰居的DNMSPSO算法[11];

(3)基于綜合學習的CLPSO算法[12];

(4)基于協同量子的CQPSO算法[13]。

本文實驗采用Matlab7.8進行仿真,系統軟硬件環境為:2.20 GHz,4.00 GB內存,Windows7操作系統。實驗中,DGPSO算法與PSO算法[2]慣性權重最大值設為0.9,最小值設為0.4,學習因子c1=1.7,c2=2.05,DNMSPSO算法的參數設置與文獻[11]中的一致,CLPSO算法的參數設置與文獻[12]中的一致,CQPSO算法的參數設置與文獻[13]中的一致。5個算法的最大迭代次數均設置為1 000次,粒子數目為30個,維數為30維,DGPSO算法的子種群數目集合為S=[2,3,5,6,10],測試函數如表1所示,取50次運行結果的平均值。

DGPSO算法的時間復雜度為O(N×D×maxiter),其中,N為粒子群數目;D為粒子維數;maxiter表示粒子群優化的最大迭代次數。

表2為5個算法在12個測試函數上的實驗結果,其中,最差解和最好解分別表示在50次獨立運行中,算法找到的最差的最優解和最好的最優解。均值表示在50次獨立運行中,算法最優解的平均值。方差表示50次獨立運行中,算法的穩定性。為了準確判定算法的優化能力,取上述測試指標中的均值和方差作為評價標準。

表2 4種算法在測試函數上的實驗結果

由表2的均值和方差結果可以看出DGPSO算法的實驗結果,除了在f1函數的優化性能比CQPSO算法[13]稍差,f2～f12測試函數的實驗結果都明顯優于其他算法,其收斂精度和穩定性較好。

圖4～圖9給出了5種算法在6個測試函數中的迭代進化曲線對比,為了便于觀察,將各算法尋找到的最優解進行取對數操作。可以看出,本文提出的DGPSO算法在收斂速度上具有明顯優勢,可以有效跳出局部最優,且算法搜索到的解的精度高。由于篇幅有限,本文只列舉了6個測試函數的對比圖,在其他測試函數上算法也具有相似的性能。

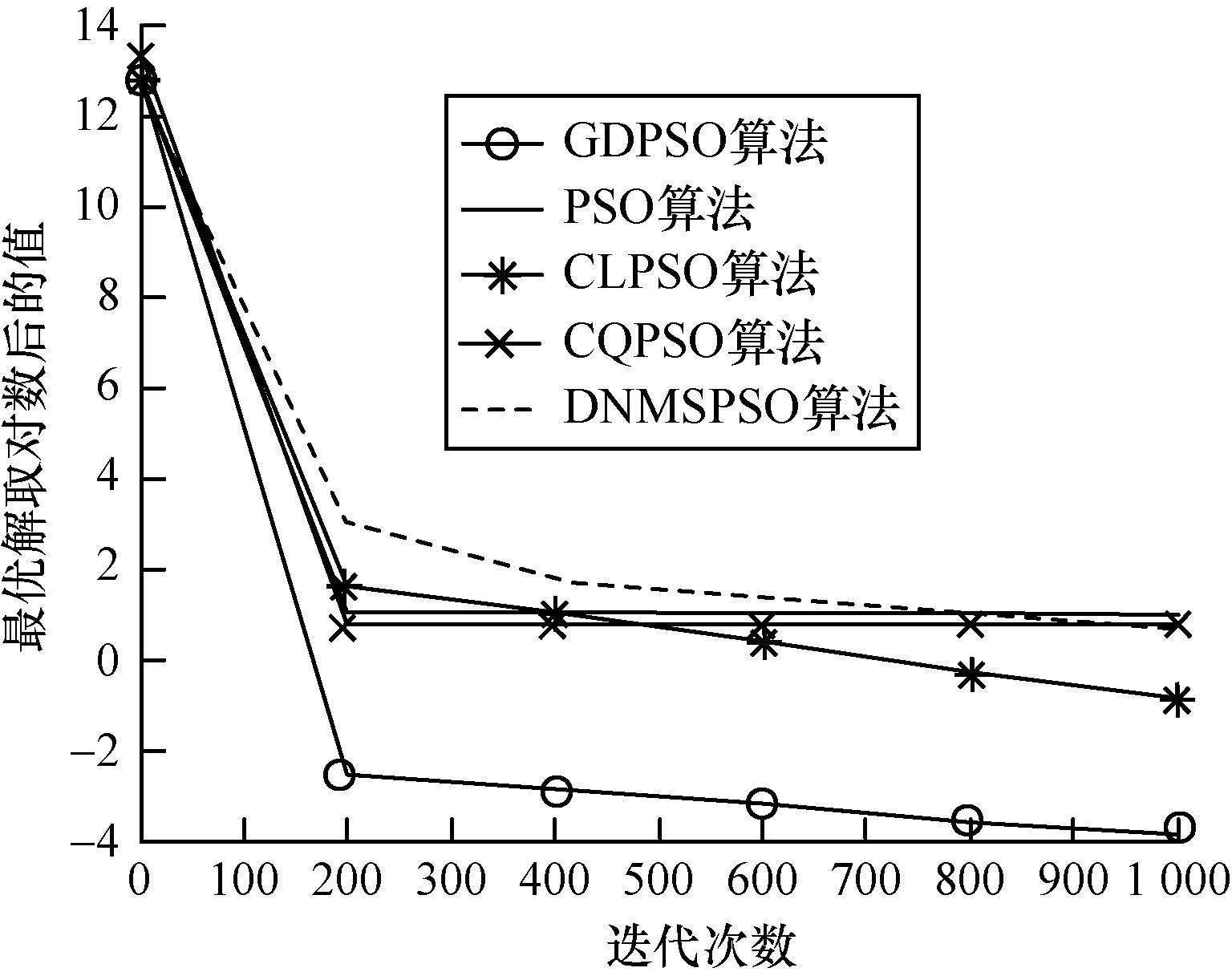
圖4 算法在f3函數上的迭代效果

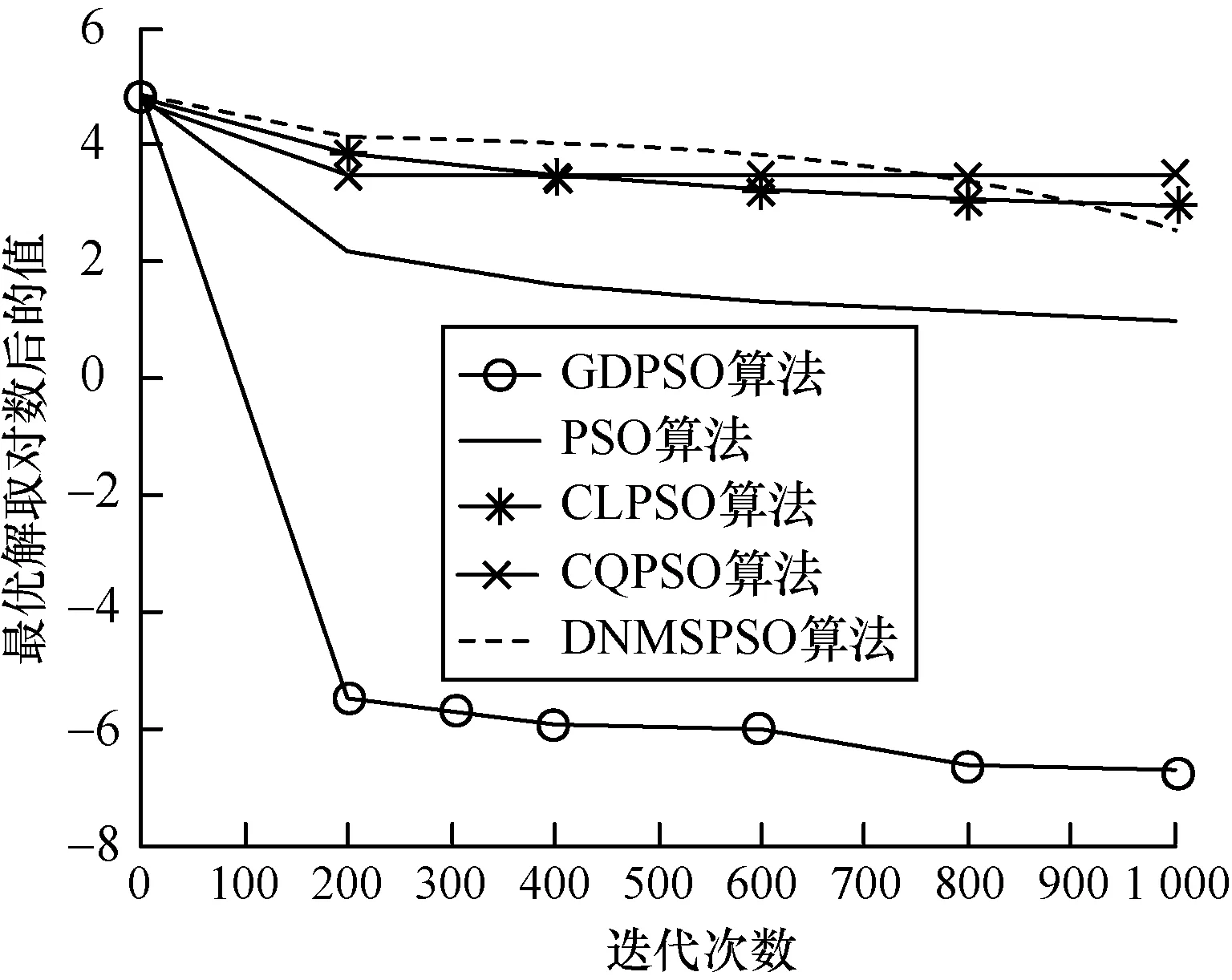
圖5 算法在f4函數上的迭代效果

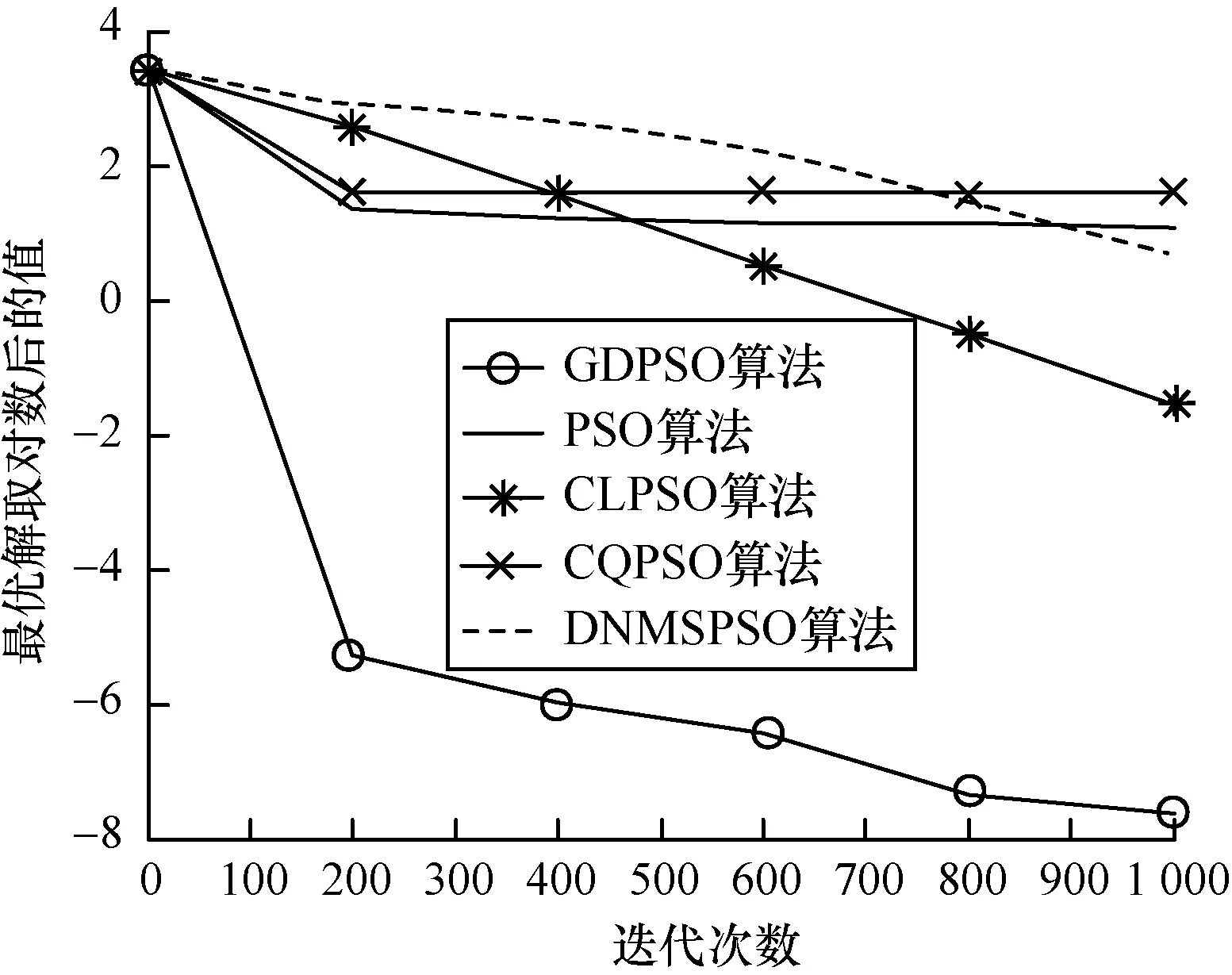
圖6 算法在f5函數上的迭代效果

圖7 算法在f7函數上的迭代效果

圖8 算法在f11函數上的迭代效果

圖9 算法在f12函數上的迭代效果

5 結束語

本文提出一種采用動態隨機劃分子種群策略的粒子群優化算法。該算法能增加交互粒子劃分到同一個子種群的概率,避免不同子種群搜索范圍可能相同的情況,幫助種群跳出局部最優。理論分析和實驗結果表明,DGPSO算法能有效利用粒子的共享信息、擴大種群的搜索范圍、提高算法的尋優性能以及處理復雜多峰問題的能力。

[1] Kennedy J,Eberhartr C.Particle Swarm Optimization[C]// Proceedings of IEEE International Conference on Neural Networks.Perth,USA:IEEE Press,1995:1942-1948.

[2] Shi Yuhui,EberhartR.A Modified Particle Swarm Optimizer[C]//Proceedings of 1998 IEEE International Conference on World Congress on Computational Intelligence.Anchorage,USA:IEEE Press,1998:69-73.

[3] Eberhart R C,Shi Y.Comparing Inertia Weights and Constrict in Factors in Particle Swarm Optimization[C]// Proceedings of 2000 Congress on Evolutionary Computation.San Diego,USA:IEEE Press,2000:84-88.

[4] van den Bergh F,Engelbrecht A P.Effects of Swarm Size on Cooperative Particle Swarm Optimizers[C]//Proceedings of the 3rd Genetic and Evolutionary Computation Conference.San Francisco,USA:IEEE Press,2001.

[5] Chatterjee A,Siarry P.Nonlinear Inertia Weight Variation for Dynamic Adaptation in Particle Swarm Optimization[J].Computers&Operations Research,2006,33(3): 859-871.

[6] Zhan Z H,Zhang J,Li Y,et al.Adaptive Particle Swarm Optimization[J].IEEE Transactions on Systems,Man,and Cybernetics,2009,39(6):1362-1381.

[7] van den Bergh F,Engelbrecht A P.A Cooperative Approach to Particle Swarm Optimization[J].IEEE Transactions on Evolutionary Computation,2004,8(3):225-239.

[8] Niu B,Zhu Y,He X.Multi-population Cooperative ParticleSwarm Optimization[C]//Proceedings of ECAL’05.Berlin,Germany:Springer,2005:874-883.

[9] 呂 林,羅 綺,劉俊勇,等.一種基于多種群分層的粒子群優化算法[J].四川大學學報:工程科學版, 2008,40(5):171-176.

[10] Liang J J,Suganthan P N.Dynamic Multi-swarm Particle Swarm Optimizer with Local Search for Large Scale Global Optimization[C]//Proceedings of IEEE World Congress on Computational Intelligence.Hong Kong,China:[s.n.], 2008:3845-3852.

[11] 劉衍民,趙慶禎,隋常玲,等.一種基于動態鄰居和變異因子的粒子群算法[J].控制與決策,2010,25(7):968-974.

[12] Liang J J,Qin A K,Suganthan P N,et al.Comprehensive Learning Particle Swarm Optimizer for Global Optimization of MultimodalFunctions[J].IEEE Transactionson Evolutionary Computation,2006,10(3):281-295.

[13] Li Yangyang,Xiang Rongrong,Jiao Licheng,et al.An Improved Cooperative Quantum-behaved Particle Swarm Optimization[J].Soft Computing,2012,16(6):1061-1069.

編輯 陸燕菲

A Particle Swarm Optimization Algorithm of Dynamic Grouping

WANG Yanyan1,GE Hongwei1,WANG Juanjuan2,YANG Jinlong1
(1.College of Internet of Things Engineering,Jiangnan University,Wuxi 214122,China; 2.Weifang Power Supply Company,State Grid Corporation of China,Weifang 261021,China)

Aiming at Particle Swarm Optimization(PSO)algorithm is easy to fall into local optimal problems,this paper puts forward a PSO algorithm of dynamic group.Through the study of the flock behavior,the concept of interacting particles is presented.It introduces dynamic groupings into the PSO algorithm.Population is divided into multiple sub populations dynamically,and the number of each division of sub populations is randomly selected from a specific set.It increases the probability of interacting particles into the same sub population.During converging evolution,each sub population uses the ring topology structure to increase the diversity of population and the global search ability of the algorithm.Experimental results show that compared with other PSO algorithms,the algorithm has better optimal performance,stability,and higher convergence precision.

Particle Swarm Optimization(PSO);local optimum;global optimum;interacting particle;dynamic grouping;ring topology

1000-3428(2015)01-0180-06

A

TP18

10.3969/j.issn.1000-3428.2015.01.033

國家自然科學基金資助項目(61305017);江蘇省自然科學基金資助項目(20130154);江蘇高校優勢學科建設工程基金資助項目。

王燕燕(1986-),女,碩士,主研方向:粒子群優化算法;葛洪偉,教授;王娟娟,工程師;楊金龍,副教授。

2014-01-21

2014-02-20 E-mail:wangyanyanever86@163.com

中文引用格式:王燕燕,葛洪偉,王娟娟,等.一種動態分組的粒子群優化算法[J].計算機工程,2015,41(1):180-185.

英文引用格式:Wang Yanyan,Ge Hongwei,Wang Juanjuan,et al.A Particle Swarm Optimization Algorithm of Dynamic Grouping[J].Computer Engineering,2015,41(1):180-185.