小型電力系統穩定性分析的改進算法及其應用

田 野,沈愛弟,王良秀,王 樂

(1.上海海事大學航運技術與控制工程交通行業重點實驗室,上海201306; 2.中國船舶重工集團公司第七O四研究所,上海200031)

小型電力系統穩定性分析的改進算法及其應用

田 野1,沈愛弟1,王良秀2,王 樂2

(1.上海海事大學航運技術與控制工程交通行業重點實驗室,上海201306; 2.中國船舶重工集團公司第七O四研究所,上海200031)

針對電力系統穩定性分析運算時間長、穩定域過于保守等問題,提出一種改進算法分析小型電力系統的暫態穩定性。基于能量函數法,利用平方和分解法得到李雅普諾夫函數,使用粒子群優化算法求其臨界能量,改造李雅普諾夫函數擴張穩定域,以達到穩定域邊界逼近實際邊界的目的,采用Matlab對電力系統的穩定性進行仿真分析并驗證其精確度及速度。應用改進的能量函數法實時判斷當前狀態的穩定裕度,計算故障極限切除時間,了解系統崩潰的接近程度。仿真結果表明,改進算法計算速度快、易于實現、可靠性高,具有較高的工程實用性。

電力系統穩定性;能量函數法;臨界能量;粒子群優化;仿真分析

1 概述

現代電力系統是一個高維數、強非線性的復雜動力系統,其穩定性問題尤其重要。在陸上電力系統中,世界各地發生了多起由于電力系統失穩導致的大范圍停電事故,這些事故造成了巨大的經濟損失和社會影響,同時也反映出研究電力系統穩定的重要意義。

電力系統穩定性是指電力系統受到事故擾動后保持穩定運行的能力。目前暫態能量函數法的發展動態無外乎從提高計算速度和改善精度兩方面進行理論和在線應用研究[1]。文獻[2]提出了一種基于穩定域邊界二次近似的算法并求取暫態電壓穩定裕度指標,分析了考慮單負荷無窮大系統的暫態電壓穩定性。文獻[3]提出一種采用并聯恒阻抗的負荷模型,并應用此模型進行了暫態電壓穩定性判斷。文獻[4]建立以感應電機并聯負載為基礎的簡化電力系統,并采用二階正規型近似局部吸引域邊界。

近二十年來,研究成果相當顯著,計算速度比初期有了很大改善;求取的穩定域更加可靠,抑制了一定的保守性,暫態能量函數法進入電網穩定性分析等實際工程應用階段。

本文研究適合電力系統典型結構的暫態穩定性分析方法,利用平方和分解法計算李雅普諾夫函數,并使用粒子群優化算法求出此函數的臨界能量最優解,得到穩定域邊界,改造李雅普諾夫函數對邊界進行擴張,以逼近實際穩定域。根據系統實時配置情況,提出快速有效的電力系統實時安全裕度分析方法以及故障極限切除時間計算方法,最后使用Matlab仿真驗證算法速度、精確度與正確性。

2 改進算法設計

隨著電力系統的發展,其暫態穩定性越來越受到重視,由于時域仿真法計算量大、速度慢,且不能提供穩定裕度細節等原因,能量函數法在穩定性分析的工程應用方面占主導地位。

2.1 能量函數法

能量函數法的核心思想即不必求解微分方程,直接判斷系統穩定性,在非零初始狀態作用下的運動過程中,若能量隨時間衰減以至最終消失,則系統遲早會達到平衡狀態,即系統穩定。每個穩定的系統都有一個穩定域邊界,在穩定域邊界外的狀態點會隨著時間的增加而發散,在穩定域邊界內的狀態點會隨著時間的增加逐漸逼近穩定平衡點。假設取某能量函數V(x),定義

2=5為穩定域邊界,如圖1所示。

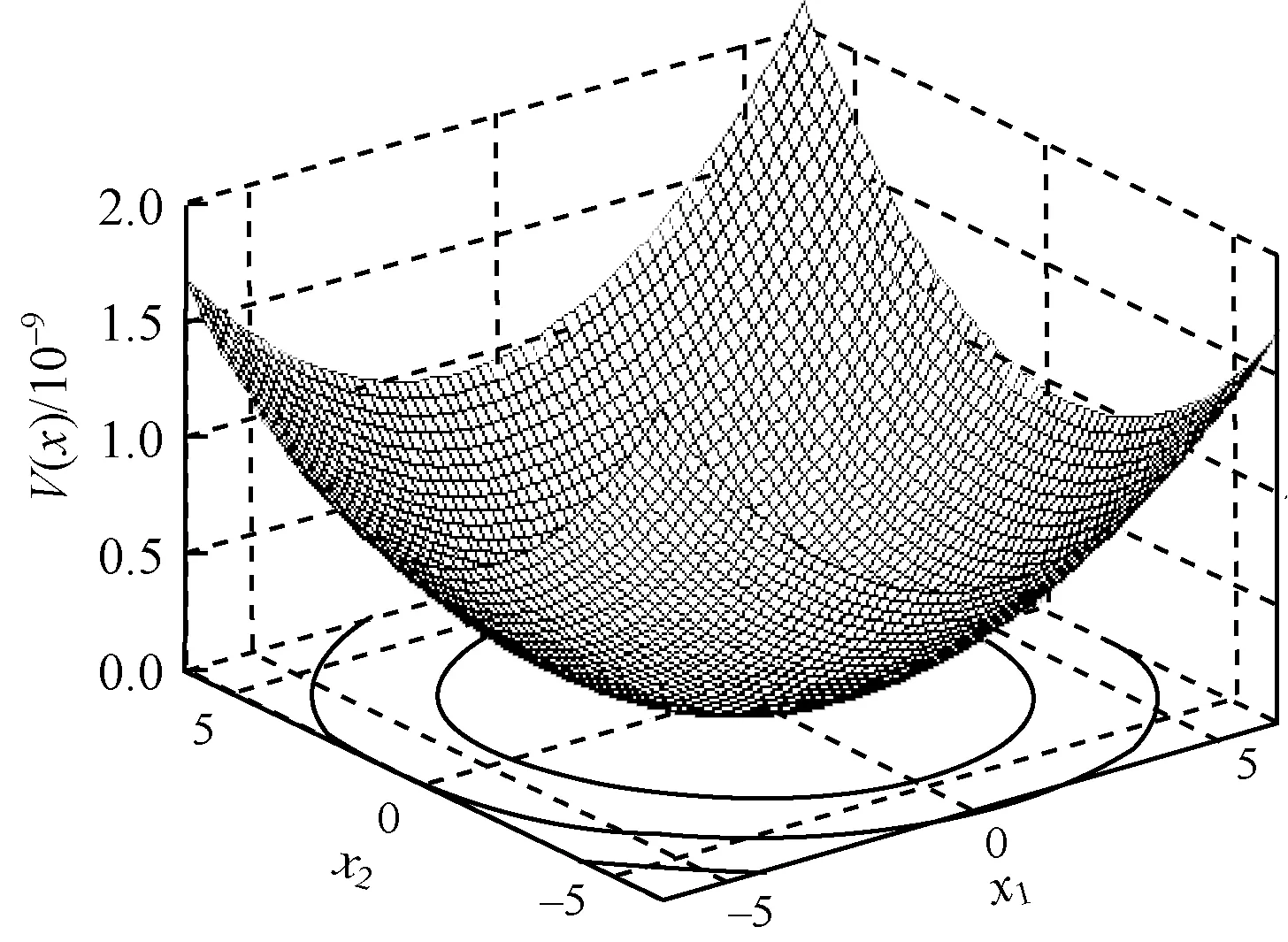
圖1 能量函數介紹

在圖1中,x軸y軸為狀態變量,z軸為能量函數值,可以看出,隨著狀態點向外延伸,能量函數的值也隨之增大,當能量函數的值超過臨界能量時,系統將會失穩,而臨界能量就是臨界穩定域邊界(x12+x2

2=5)上能量函數的值。

能量函數法主要流程為:首先能量函數法需構造一個目標系統的函數;其次判斷此函數的導數為負定,即沿著目標系統運動時是否隨時間的增長而衰減;接著計算臨界能量,目標系統的穩定域邊界就是此能量函數的某個等勢面,其函數值即為臨界能量;最后通過對狀態點能量與臨界能量的大小對比就能判斷出狀態點是否穩定。前兩個步驟費時較多,但只需離線完成,使用本文的改進算法可大大提高計算速度,實時在線情況下,只需完成最后一步即可,可瞬間判斷穩定性結論。

采用能量函數法進行暫態穩定分析的具體流程如圖2所示。通過該流程可以看出,采用能量函數法進行暫態穩定分析的2個關鍵問題是:(1)能量函數(即李雅普諾夫函數)的構造與選擇,在滿足要求的情況下盡量選擇逼近穩定域邊界的函數;(2)臨界能量最優解的計算,臨界能量的計算實質是對穩定域邊界近似基準點的計算。

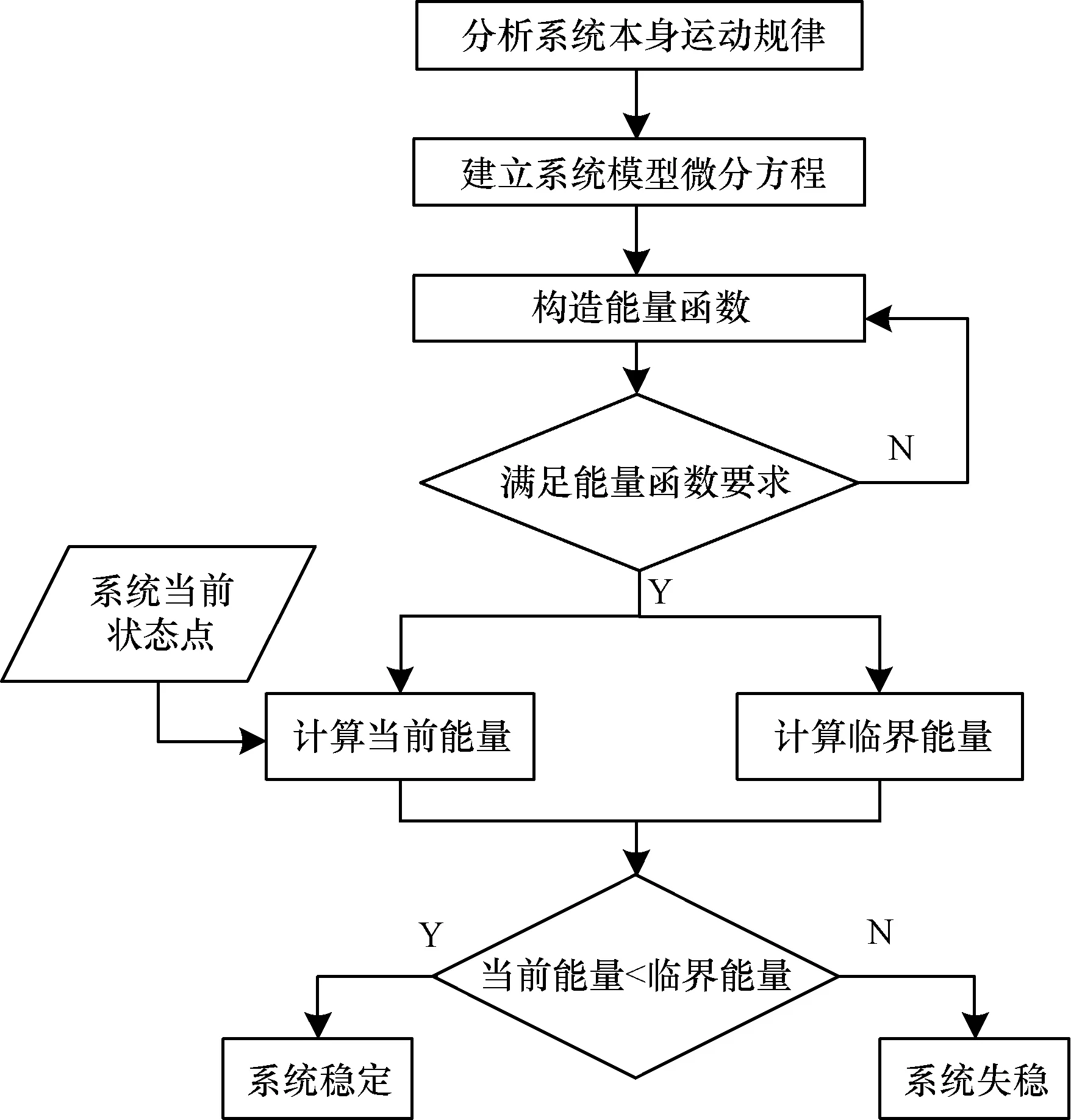
圖2 能量函數法基本流程

2.2 平方和分解法

能量函數法的一個難點是能量函數的構造與選擇,大部分李雅普諾夫函數對系統的適應性差,無法滿足要求,要構造李雅普諾夫函數適應所有的系統比較困難。為此,在本文中采用基于平方和分解法自動計算李雅普諾夫函數,文獻[5]證明此能量函數適用于所有多項式系統,計算量較小,但得到的穩定域具有一定的保守性,且非多項式系統須轉化為多項式系統方可應用。首先給出李雅普諾夫函數的要求,需滿足以下3點,即李雅普諾夫定理:

定理1李雅普諾夫定理

(1)V(x,t)正定且有界,β(‖x‖)≥V(x,t)≥α (‖x‖)＞0;

(2)(x,t)負定且有界,(x,t)≤-γ(‖x‖)＜0;

(3)‖x‖→∞,則V(x,t)→∞。

所包含的3個條件對于高于四階的多項式系統是非常苛刻的,想要獲得滿意的穩定域邊界更加困難。一個檢驗多項式非負的充分條件是它滿足平方和分解,,得到以平方和表示的李雅普諾夫函數,本文中將分別采用多種平方和能量函數驗證算法的正確性。

2.3 粒子群優化算法

能量函數法的另外一個難點是臨界能量的求取,以往的能量函數法一般采用遺傳算法(GA)求取臨界能量的最優解[6],但是遺傳算法收斂速度慢、參數復雜等缺點限制了它的發展,在本文中將采用粒子群優化算法代替遺傳算法進行最優解的求取。

此算法具有自我學習提高和向他人學習的雙重優點,從而能在較少的迭代次數中找到最優解,大大減少了計算時間,其概念簡單、易于實現,同時又有深刻的智能背景,既適合科學研究,又特別適合工程應用[7]。

其大致步驟可分為5步[7-8],如圖3所示:

(1)設定粒子位置的上下限,并隨機初始化粒子群中每個粒子的位置和速度。

(2)根據系統方程計算每個粒子的適應度。

(3)記錄粒子計算過具有最好適應度的位置(個體最優解),并記錄群中所有粒子計算過的最好位置(全局最優解)。

(4)依據公式:

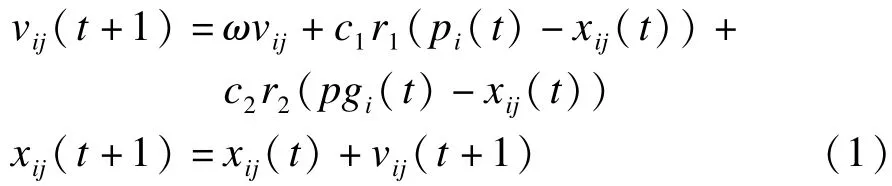
對粒子的速度和位置進行優化。其中,xij表示群體中i粒子的位置為j;vij是它對應的速度;ω為慣性權重;c1,c2為加速度常數(學習速率);r1,r2為[0,1]均勻分布的隨機數,式(1)也是粒子群優化算法的核心。

(5)結束條件為:全局最優解的適應度滿足要求或達到設定的迭代次數,否則返回步驟(2),重新計算此流程。

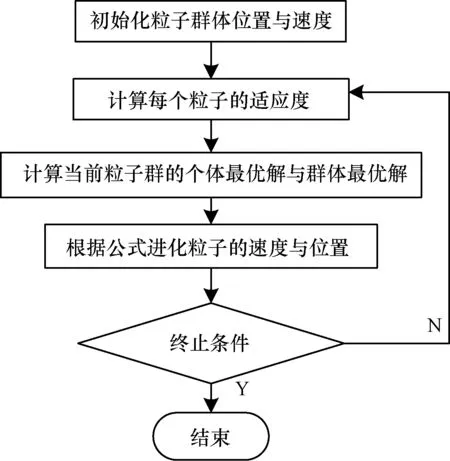
圖3 粒子群優化算法流程

2.4 穩定域的擴張

由于能量函數法的特性,函數的形狀不可能完全擬合實際穩定域邊界,即使是采用粒子群優化算法計算出的臨界能量,計算得來的穩定域邊界也常常顯得保守。本文采用后向歐拉積分法[9]對李雅普諾夫函數進行改造,以對穩定域邊界擴張,減小保守性,得到的結果令人滿意。

如圖4所示,最內層的為初始能量函數穩定域,中心為穩定平衡點,中間層為擴張能量函數穩定域,最外圍的是實際穩定域。使用文獻中的擴張法,通過逆向時間積分將狀態點向外擴張,將穩定域逐漸擴大,理論情況下能完全逼近實際穩定域。

圖4 能量函數擴張示意圖

算法實際上是能量函數沿系統積分曲線擴張的近似,考慮各類算法的計算量和精確性,采用后向歐拉積分的能量函數擴張算法。對非線性系統的能量函數V(x),構造如下的迭代序列:

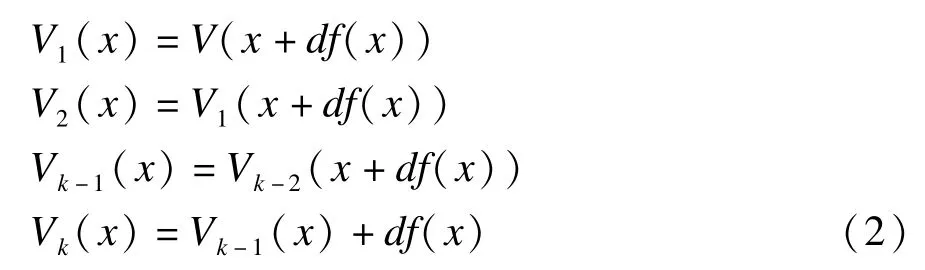
其中,d為迭代步長;k為迭代次數。

此算法既是在足夠小的迭代步長下,用d×f(x)來代替很小一部分積分曲線,通過多次迭代擴展到一個較大部分,穩定域邊界得以擴張,故d的選取要適當小,但太小則不能體現出擴張效果,另一方面,由于積分過程的收斂性限制,參數d不能選得太大,因此需要的擴張迭代次數k要盡可能大,但會影響運算速度,根據仿真經驗可求得滿意的k值。

2.5 算法總結

在工程應用中一般計算不出整個穩定域,也無需求出,判斷狀態點是否在穩定域邊界內即可。實時判斷當前狀態的穩定裕度,計算故障極限切除時間[10],了解系統對崩潰的接近程度是十分重要的,如圖5所示為大擾動下系統穩定裕度k與故障極限切除時間t的算法流程圖,其總結了上述所有算法。在系統穩定的情況下當k越接近1,穩定裕度越大,即離系統崩潰越遠。

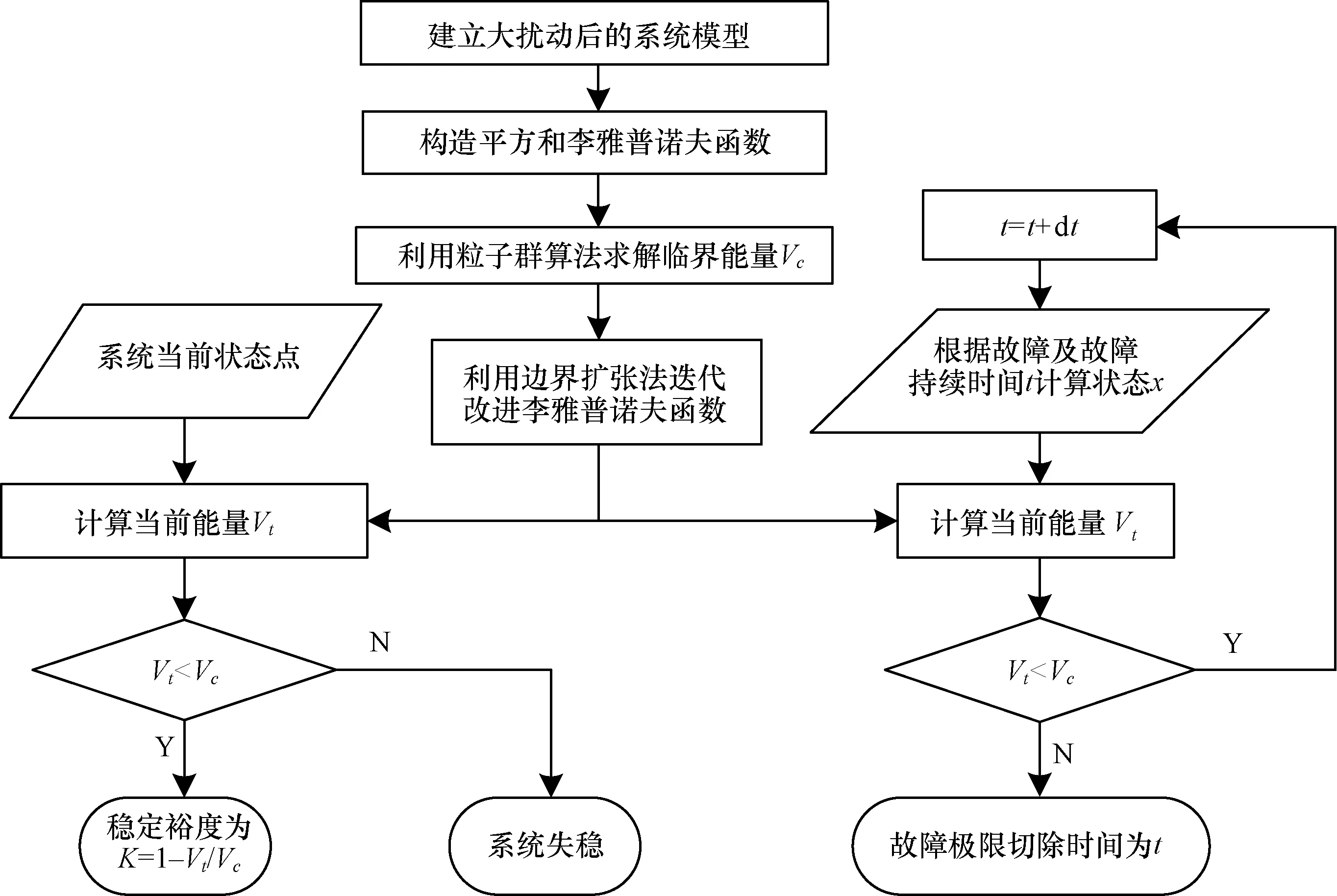
圖5 大擾動下的算法流程

3 系統模型的建立

本文使用簡化的三機系統以及電力系統綜合模型這2種經典的系統模型來驗證改進算法的正確性。此2種模型均大量被其他文獻引用驗證,具有一定的參考性。

3.1 簡化的三機系統

此系統作為常用的電力系統模型被廣泛應用于穩定性研究中[11-12],因為其擬穩定域邊界可近似求出,并能作為真實穩定域邊界[12],所以將其作為驗證穩定性分析方法精確度的簡單系統。并且由于這是二維系統,便于觀測穩定域的圖形,以達到視覺上的直觀對比。簡化三機系統模型如式(3)所示[11]:

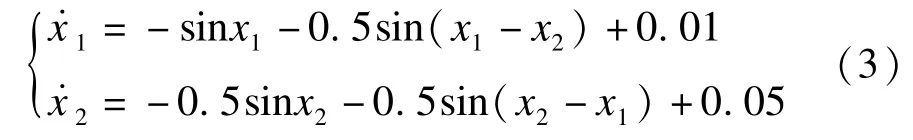
使用平方和分解法求李雅普諾夫函數V(x)的前提條件是多項式系統。此非多項式系統包含三角函數,需進行多項式轉化才得以求得李雅普諾夫函數,系統穩定平衡點為xsep(0.028 01,0.064 03),通過泰勒公式式(4)將系統方程在平衡點進行二次展開:

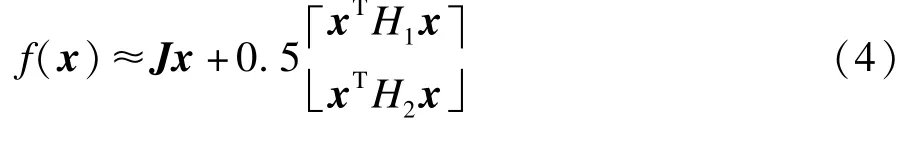
為驗證分析方法的精確度,需與實際穩定域作比較,而高階系統的實際穩定域一般極難得到,而對于簡化的三機系統,能通過以下定理得到系統實際穩定域[12]:

定理2若系統存在能量函數,其漸近穩定平衡點xsep所對應的擬穩定域邊界?S(xsep)由邊界上I型不穩定平衡點的穩定流形的閉包組成。

所謂I型不穩定平衡點即系統雅克比矩陣J=有1個正實部特征值。此系統中所有5個不穩定平衡點均為I型不穩定平衡點,所以在系統的所有平衡點中選取不穩定平衡點為起始點對系統做逆向時間積分,在Matlab中用ode45函數就能快速完成,即可得到擬穩定域邊界,并判斷此邊界是否為閉包,這可以近似看作系統的實際穩定域邊界以驗證研究的精確度。

3.2 綜合電力系統模型

綜合電力系統模型是所有電力系統模型的基礎,由原動機-PI調速器、同步發電機、PI勵磁系統和恒功率負載組成,發生擾動(如三相接地短路故障),一段時間內恢復正常。

系統模型如圖6所示。

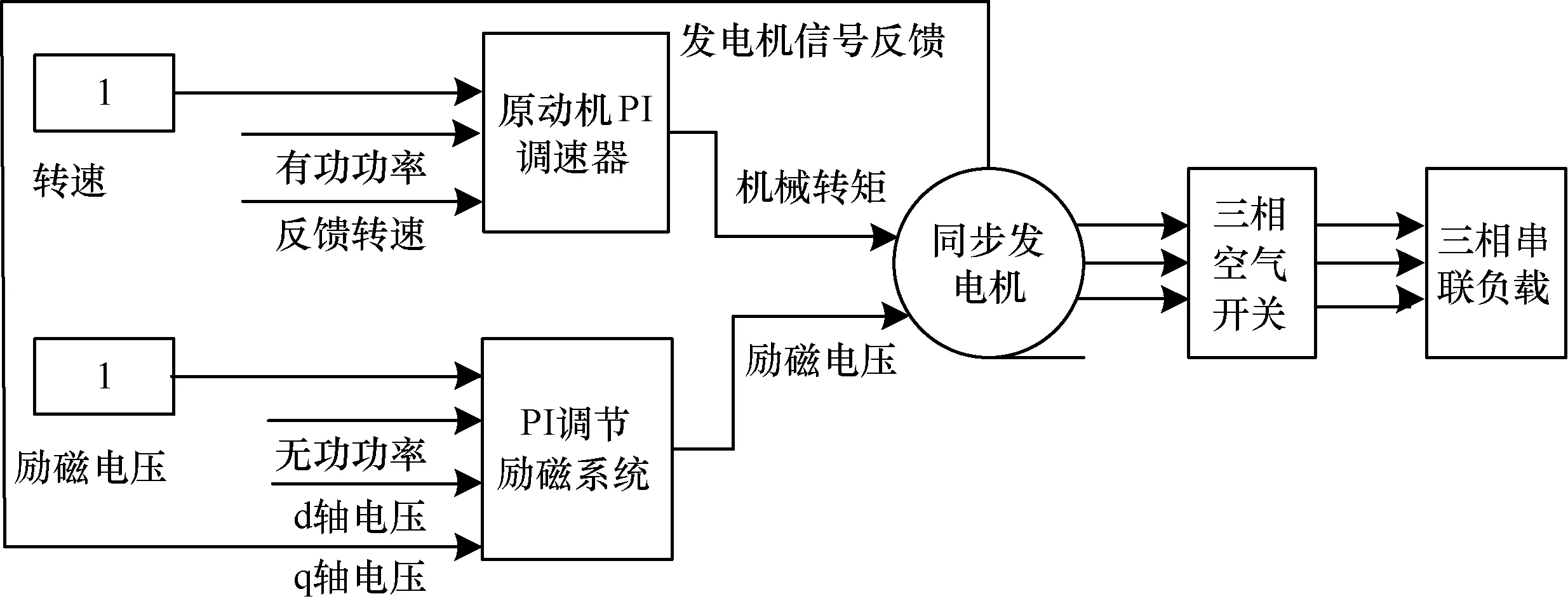
圖6 綜合電力系統模型

原動機-PI調速器:

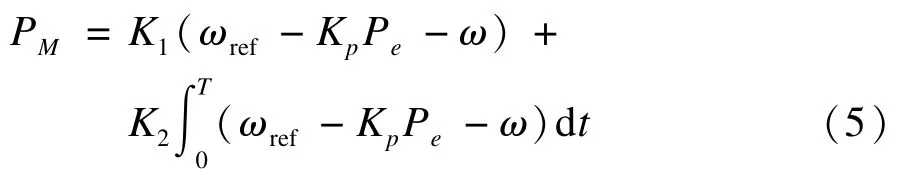
其中,PM為機械功率;K1,K2為PI系數;ωref為給定轉速;Kp為有功功率下垂系數;Pe為有功功率,令:

則公式化為式(7):

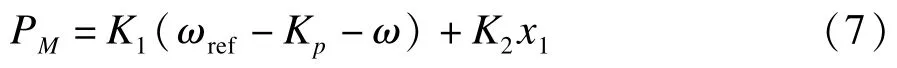
同步發電機三階模型:

其中,θ為機械角度;Tj為慣性系數;Eq′為q軸暫態電勢;id,iq為dq軸電流;D為摩擦系數;xd,xd′,xq,xq′為dq軸電抗和暫態電抗;T′do為開路暫態時間常數。

PI調節勵磁系統:

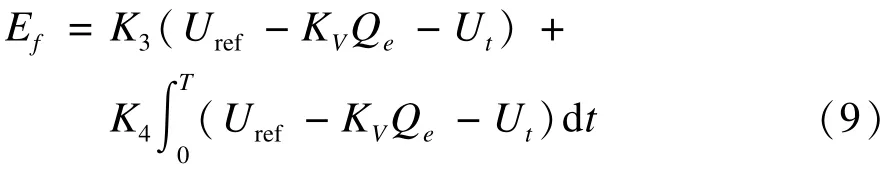
其中,Ef為勵磁電壓;K3,K4為PI系數;Uref為給定電壓;KV為無功功率下垂系數;Qe為無功功率;令:

則公式化為式(11):

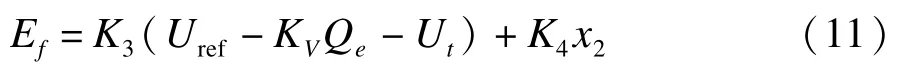
將式(5)、式(7)、式(8)、式(11)聯立即得到完整的綜合電力系統模型。

4 仿真與分析

根據上述系統模型與算法流程,采用Matlab對簡化的三機系統以及綜合電力系統模型進行仿真以驗證算法的正確性及精確度。

通過多次仿真結果發現,粒子群個體數目選為50,迭代次數為50比較合適,不僅提高了精確度,而且保證了速度優勢。通過多次仿真結果發現,當采用改進李雅普諾夫函數法進行邊界擴張時,d取0.1,k取5(即迭代5次),取此值時穩定域達到一定的擴張,且并不過多影響運算速度。

對于簡化三機系統模型取文獻[11]的能量函數及臨界能量作為比較,其能量函數為式(12):

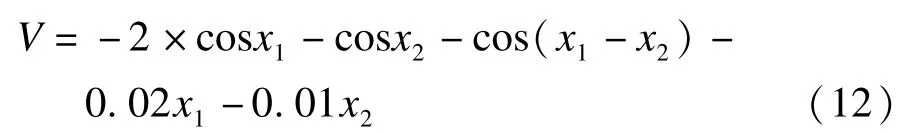
圖7～圖9為三機系統采用2次、4次、6次李雅普諾夫函數估計的穩定域邊界與真實穩定域邊界的對比,4次和6次因函數過長,這里不再列出,2次能量函數為式(13):

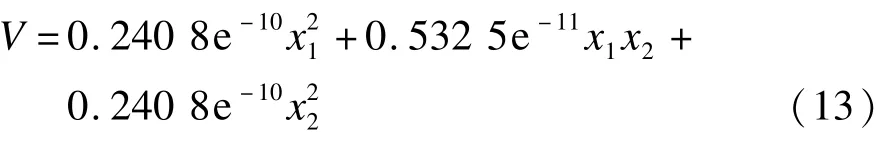
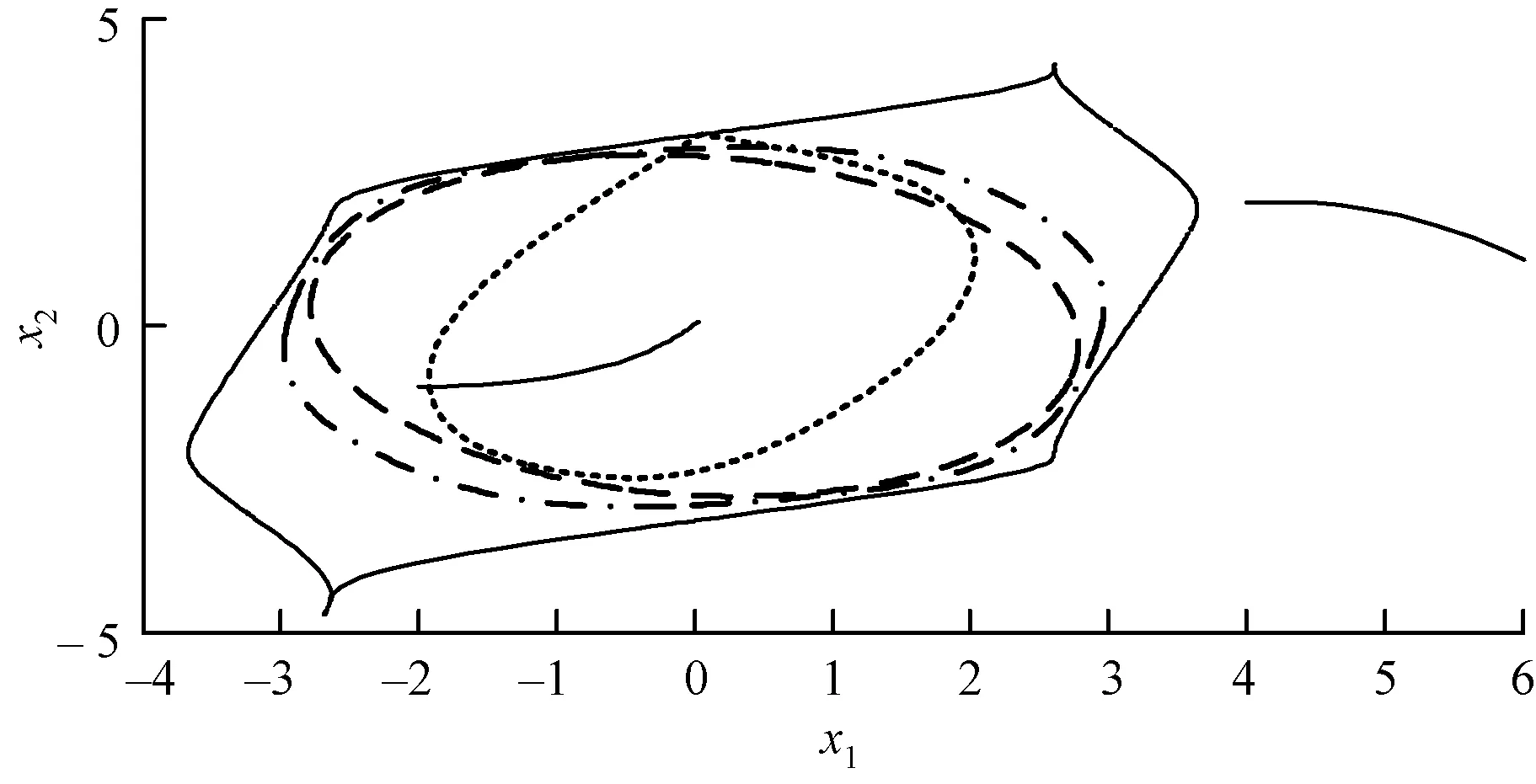
圖7 2次李雅普諾夫函數穩定域邊界對比

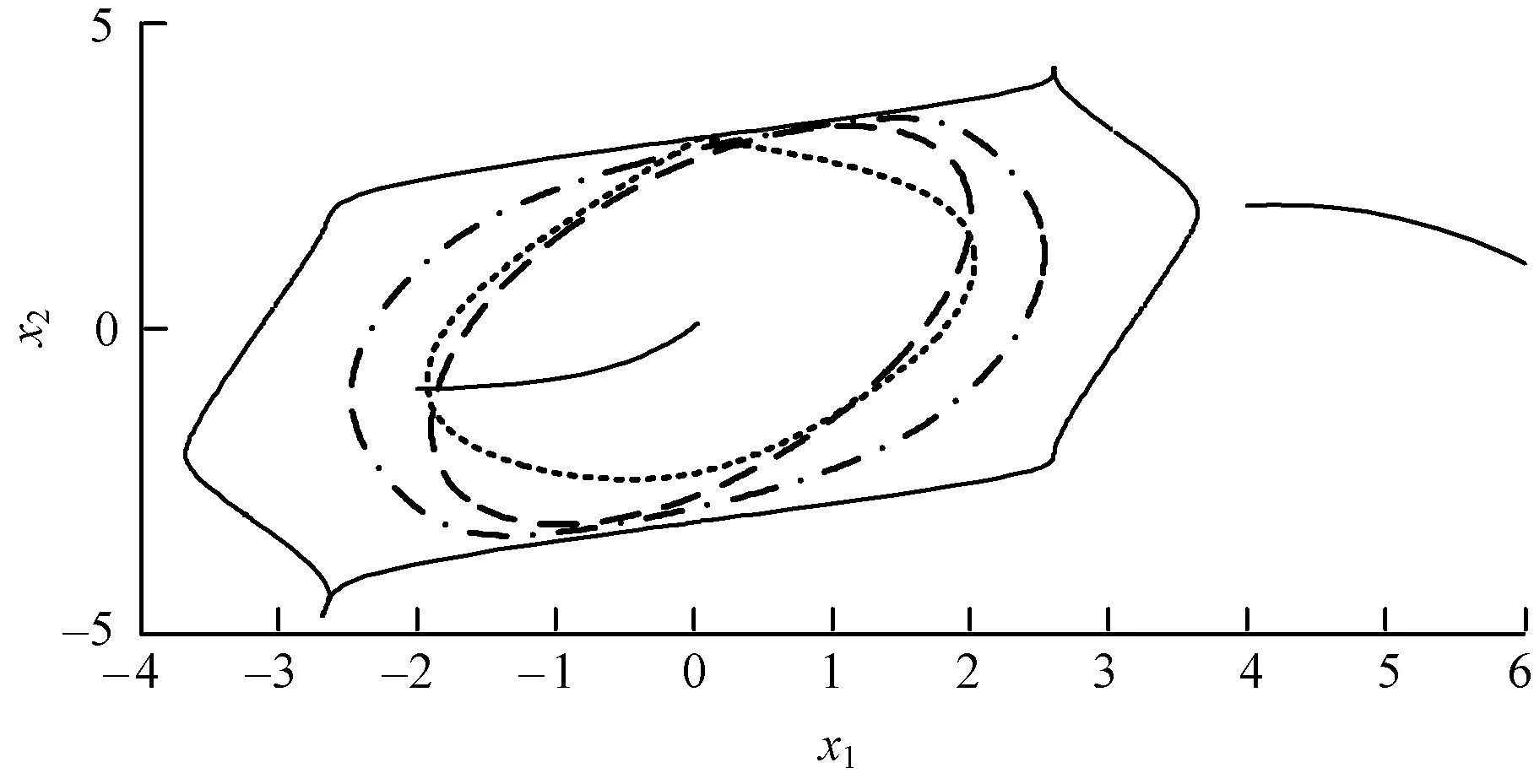
圖8 4次李雅普諾夫函數穩定域邊界對比

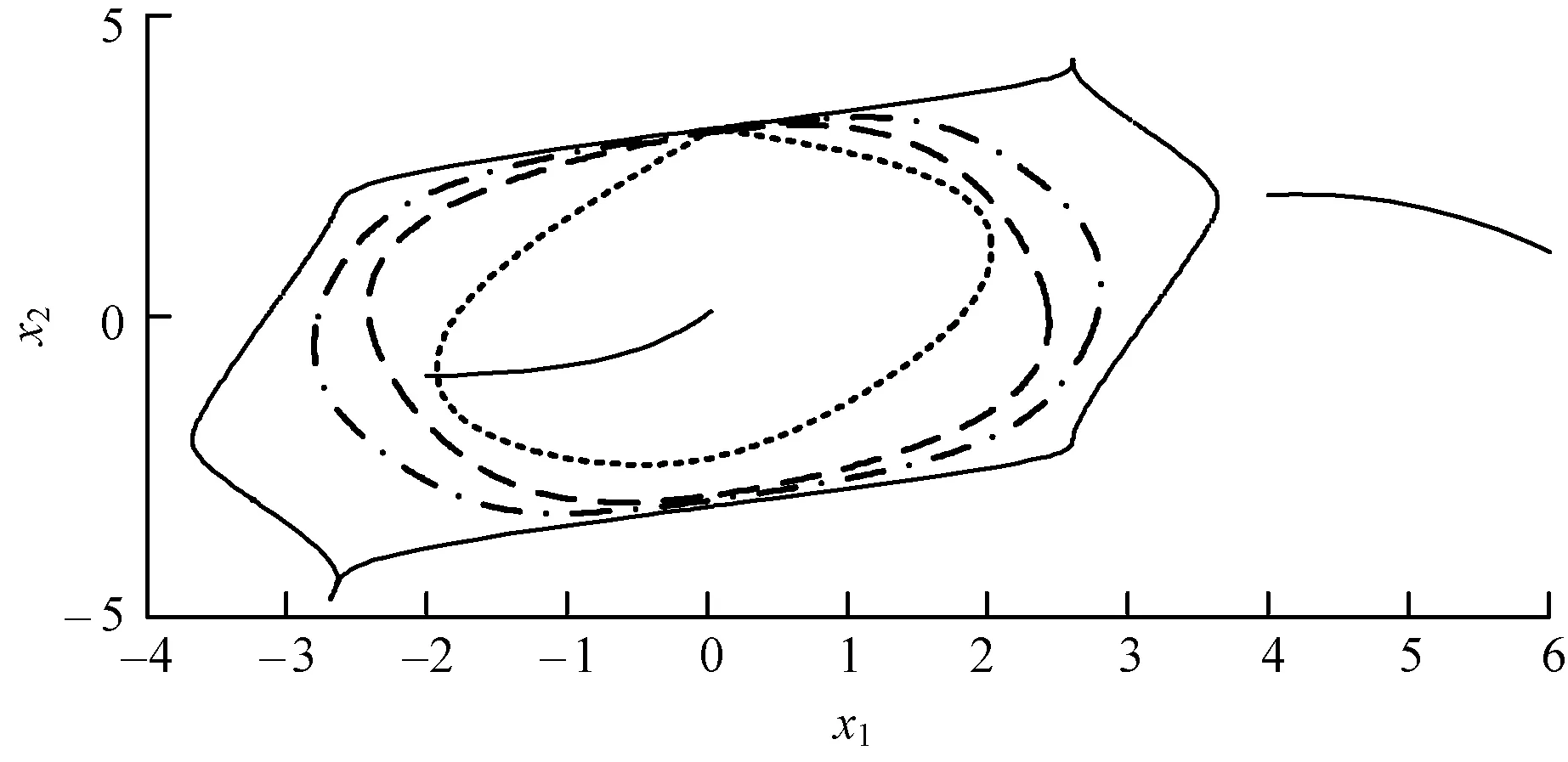
圖9 5次李雅普諾夫函數穩定域邊界對比

圖中實線代表實際穩定域邊界,即是由逆向時間積分求得的擬穩定域邊界;點線代表原始能量函數得到的穩定域邊界[12];劃線代表粒子群優化算法得到的穩定域邊界;點劃線代表使用粒子群優化算法后并對李雅普諾夫函數進行改造得到的擴張穩定域,即使用改進能量函數法得到的穩定域。圖中粗線分別給出了系統在不同初值(-2,-1)和(4,2)時,狀態變量的時域變化曲線。當狀態點在實際穩定域邊界外,運行點發散,系統失穩,而當狀態點在實際邊界內時,運行點逐漸向平衡點收斂,系統穩定。這說明了所求的實際穩定域與通過改進能量函數法計算得出的穩定域均是有效的。

假設系統實際穩定域面積為1,通過圖7～圖9計算各算法得到的穩定域邊界面積,可觀察各算法的保守性,如表1所示。

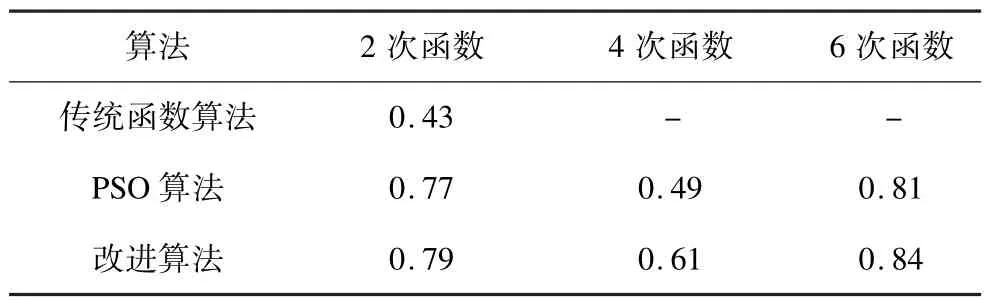
表1 穩定域面積比較

由圖7～圖9以及表1可看出,傳統穩定域遠小于PSO穩定域,而改進能量函數法得到的穩定域更為擴張;2次以及6次函數得到的穩定域較好地抑制了保守性,達到實際穩定域的約80%,6次函數為最優;而4次函數效果較差,僅比傳統算法略好。

為在數值上直觀比較各方法的精確度,使用2.5節的算法在狀態點[-2,-1]對系統的穩定裕度進行計算,如表2所示。

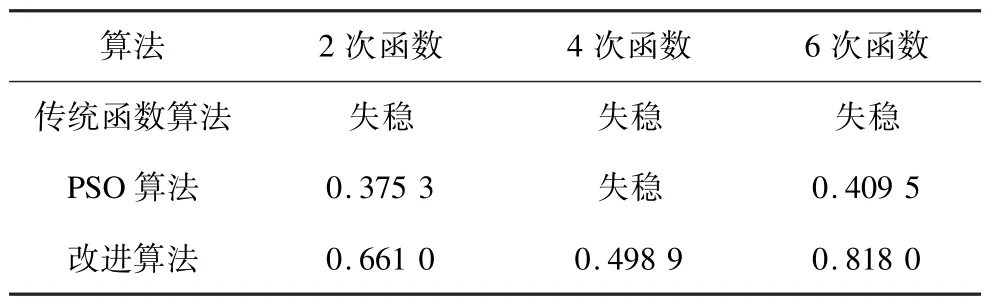
表2 狀態點[-2,-1]穩定裕度比較

由表2能看出,由于選取的狀態點均臨近穩定域邊界處,傳統函數算法對此狀態點的穩定判斷錯誤,而改進算法中6次函數得到的穩定裕度更接近1,優于2次函數及4次函數的結果,改進算法優于未使用此方法的結果,6次改進算法得到的結果最優。故障極限切除時間因在此系統中無法給出故障方程,沒有比對意義,這里不作計算比較。

圖10為2次改進算法在狀態點橫坐標在區間[-4,4],縱坐標在區間[-5,5]內得到的穩定裕度。可以看出當狀態點超出預定范圍,穩定裕度為0,即此時系統失穩,而系統穩定裕度最佳狀態點在中心部分,有且僅有一點,穩定裕度值為1。

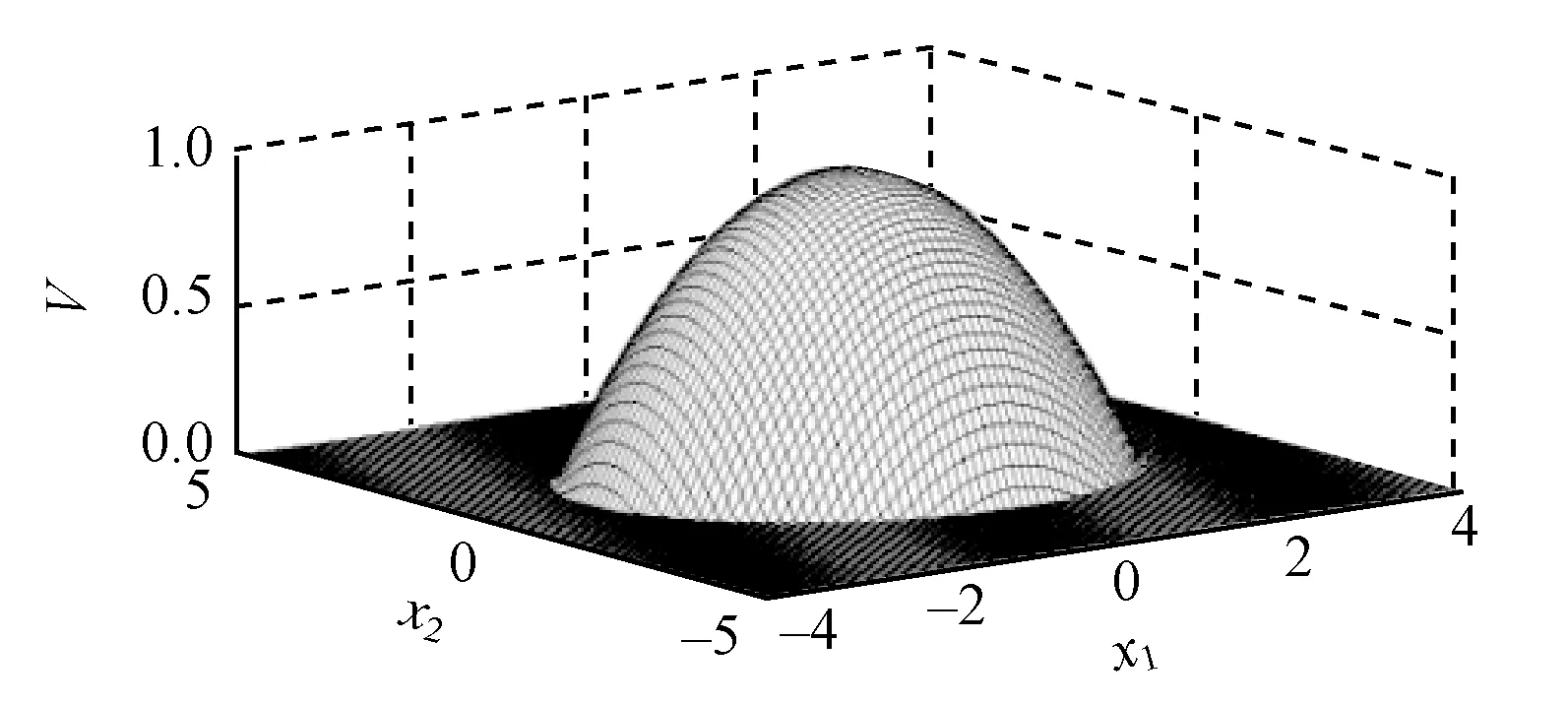
圖10 二次改進算法穩定裕度

表3為各算法的計算時間,由于系統較小且設定了較大的迭代次數以確保臨界能量值為最優,因此遺傳算法與改進算法的計算時間差距較小;但達到誤差小于1%的臨界能量最優值時,遺傳算法用時約30 s,粒子群優化算法僅需約16 s,大大減少了計算時間。傳統算法由于參考了文獻中的數值和函數,計算時間無法給出。

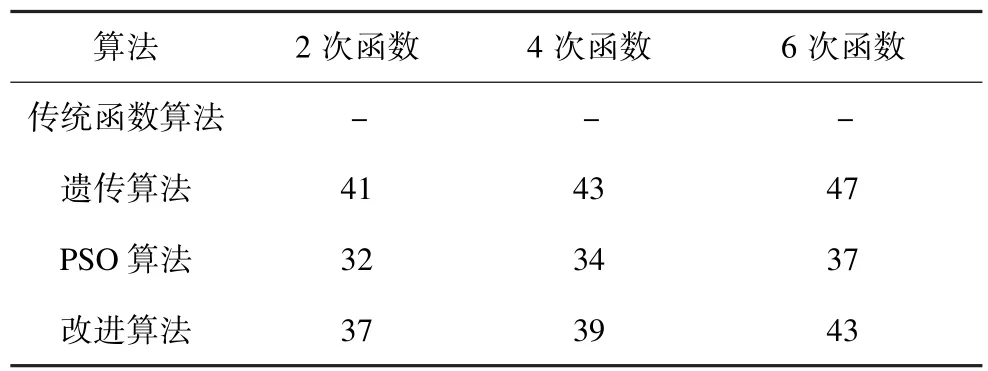
表3 各算法穩定性計算時間比較 s

縱觀本文系統所有的仿真結果,改進算法較傳統算法和大部分優化算法相比運算速度上有明顯優勢,且較好地抑制了保守性,易于實現,收斂速度快,可靠性高,穩定域邊界基本滿足要求。

隨后針對綜合電力系統模型進行分析,應用本文算法求得2次能量函數為:

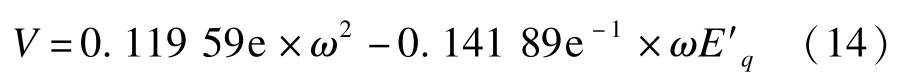
計算得系統在能量函數下的臨界能量為3.787 1;隨后進行能量函數穩定域擴張,即可代入當前狀態點求得當前能量并與臨界能量比較,并求取穩定裕度。

發電機穩定運行下,突加恒功率負載,當機端電壓小于0.8 pu時,視為系統失穩。此時狀態變量為[1,1.01,-0.01,-0.01],代入能量函數得到此時的能量為1.901 9＜3.787 1,穩定裕度為0.497 8。由于系統穩定裕度在[0,1]之間是穩定的,可見實驗系統是穩定的,且穩定裕度比較大,即與1比較接近。

再分析短路故障下的穩定情況,當系統帶負載穩定運行后,發生三相短路接地故障,此瞬間的狀態變量為[0.99,0,-0.01,-0.01],此時穩定裕度為4.698 7＞3.787 1,系統失穩,使用2.5節中的算法計算得到極限故障切除時間為0 s,即由于是單臺發電機組帶負載運行,在發生三相短路故障時,因沒有冗余電能拖動負載,系統當即失穩,電壓跌落至0,計算結果與情況相符。

通過Simulink仿真驗證可得到相同結論,如圖11波形所示,波形為發電機穩定運行后1 s突加0.5 pu的恒功率負載,系統穩定運行,電壓有小幅跌落。于1.5 s發生三相接地故障,且于1.6 s切除故障,系統期間電壓已低于0.8 pu,說明已失穩,再次驗證了結論的正確性。

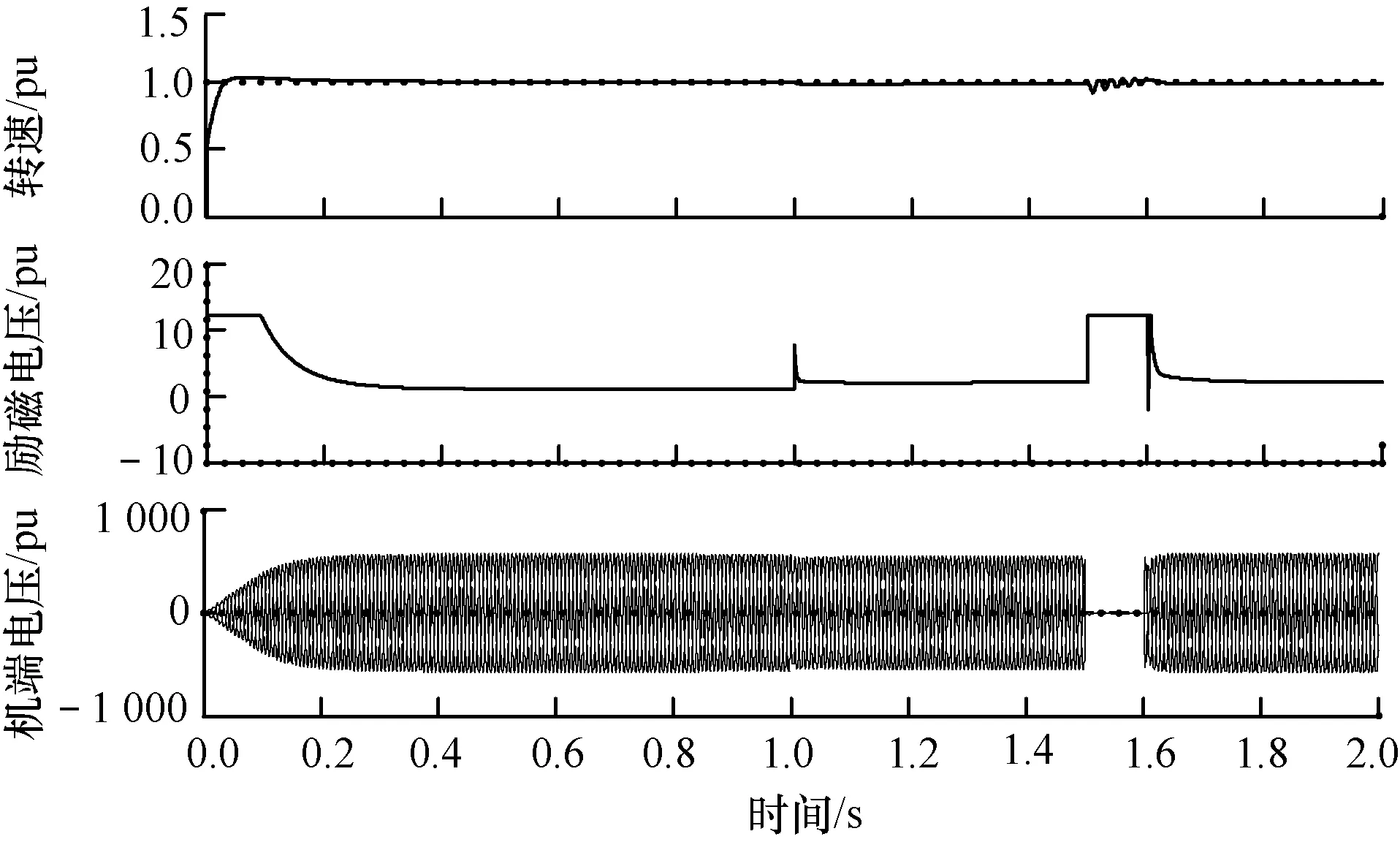
圖11 系統仿真波形

在2個不同系統中運用本文算法得到的結論與仿真實驗結論一致,驗證了所提算法的正確性。而且,此方法在線計算時間非常短,并抑制了保守性,可以滿足工程需要。

5 結束語

本文提出一種基于粒子群優化算法的改進算法,將穩定域邊界近似計算應用于暫態穩定問題的分析。通過對簡單系統中的仿真,可得到如下結論:

(1)該算法繼承了李雅普諾夫直接法的優點,計算速度快,能提供穩定裕度細節等。

(2)結合了粒子群優化算法和穩定域擴張法的綜合算法,與傳統算法相比,在求解穩定域邊界時,計算速度上有著較大的優勢,且較好地抑制了穩定域的保守性,易于實現,可靠性更高,穩定域邊界實現一定的擴張。

(3)以此算法為基礎,對于改變工況時的系統穩定指標和故障極限切除時間提出了較為全面的算法流程,適用于大部分系統,具有較好的工程實用性。

系統穩定性分析對于電力系統有著重要意義,將本文改進算法應用于電力系統是未來研究的方向。

[1] 王 川.負荷沖擊型大擾動下船舶綜合電網暫態電壓穩定性研究[D].大連:大連海事大學,2012.

[2] 王義紅,梅生偉.基于穩定裕度指標的暫態電壓穩定分析[J].電工電能新技術,2007,26(2):39-44.

[3] 林舜江,劉楊華.簡單電力系統暫態電壓穩定的直接分析法[J].湖南工業大學學報,2011,25(1):70-76.

[4] 林舜江,李欣然,劉楊華,等.考慮負荷動態模型的暫態電壓穩定快速判斷方法[J].中國電機工程學報, 2009,29(4):14-20.

[5] Chiang H.Network Reduction BCU Method and Its Theoretical Foundation[M].[S.l.]:IEEE Press,2011: 235-253.

[6] Tan W,Packard A.Stability Region Analysis Using Polynomial and Composite Polynomial Lyapunov Functions and Sum-of-Squares Programming[J].IEEE Transactions on Automatic Control,2008,53(2): 565-571.

[7] 吳建生,秦發金.基于Matlab的粒子群優化算法程序設計[J].柳州師專學報,2005,20(4):103-106.

[8] 楊淑瑩.模式識別與智能計算——Matlab技術實現[M].北京:電子工業出版社,2008.

[9] Liu Feng,Wei Wei,Mei Shengwei.On Expansion of Estimated Stability Region:Theory,Methodology,and Application to Power Systems[J].ScienceChina Technological Sciences,2011,54(6):1394-1406.

[10] 薛安成,沈 沉,梅生偉.基于穩定域邊界理論的暫態穩定指標及其應用[J].電力系統自動化,2006, 30(8):1-6.

[11] Chiang Hsiao-Dong,James S.Thorp Stability Regions of Nonlinear Dynamical Systems:A Constructive Methodology[J].IEEE Transactions on Automatic Control, 1989,34(12):1229-1241.

[12] Chiang H D,Hirsch M,Wu F F.Stability Regions of Nonlinear Autonomous Dynamical Systems[J].IEEE Transactions on Automatic Control,1988,33(1):16-27.

編輯 顧逸斐

Improved Algorithm of Stability Analysis in Small Power System and Its Application

TIAN Ye1,SHEN Aidi1,WANG Liangxiu2,WANG Le2
(1.Key Laboratory of Marine Technology and Control Engineering,Ministry of Communications, Shanghai Maritime University,Shanghai 201306,China; 2.704 Institute,China Shipbuilding Industry Corporation,Shanghai 200031,China)

This paper proposes an improved algorithm to solve the stability analysis problems of long computing time and too conservative stability ragion in small power system,such as the long time in computing,too conservative issues and so on.The algorithm is based on energy function.Use squares decomposition method to obtain Lyapunov function and use Particle Swarm Optimization(PSO)algorithm to get critical energy.Transform the Lyapunov function expand stability field in final.The algorithm can achieve stability boundary approximation of the actual boundary.Then stability of the power system is simulated and analyzed in Matlab to verify its accuracy and speed.Application of improved energy function method can determine the current state’s stability margin in real-time,calculate limited clearing fault time and understand how close the system crash is.The improved algorithm is fast to calculate,easy to achieve,and has higher reliability and better project practicality.

power system stability;energy function method;critical energy;Particle Swarm Optimization(PSO); simulation analysis

1000-3428(2015)01-0296-07

A

TP301.6

10.3969/j.issn.1000-3428.2015.01.056

科技部2012年度國際科技合作與交流專項基金資助項目“船舶電能質量監測與諧波濾除關鍵技術合作研究”(2012DFG 71850);科學技術委員會地方院校能力建設專項基金資助項目“船舶電力推進系統故障診斷與安全控制技術研究及應用”(11170501700)。

田 野(1990-),男,碩士,主研方向:系統分析;沈愛弟,高級工程師;王良秀、王 樂,工程師。

2014-03-05

2014-04-03 E-mail:tykram0821@hotmail.com

中文引用格式:田 野,沈愛弟,王良秀,等.小型電力系統穩定性分析的改進算法及其應用[J].計算機工程,2015, 41(1):296-302.

英文引用格式:Tian Ye,Shen Aidi,Wang Liangxiu,et al.Improved Algorithm of Stability Analysis in Small Power System and Its Application[J].Computer Engineering,2015,41(1):296-302.