基于二元決策圖的節點不可靠網絡可靠度計算

肖宇峰,張 華

(西南科技大學a.信息工程學院;b.特殊環境機器人技術四川省重點實驗室,四川綿陽621010)

基于二元決策圖的節點不可靠網絡可靠度計算

肖宇峰a,b,張 華a,b

(西南科技大學a.信息工程學院;b.特殊環境機器人技術四川省重點實驗室,四川綿陽621010)

針對節點不可靠網絡可靠度計算效率較低的問題,提出一種基于二元決策圖的網絡可靠度計算方法。通過因子分解得到節點可靠網絡的有序二元決策圖(OBDD),根據節點和邊的關系對邊的變量節點執行邊替換操作,生成節點不可靠網絡的OBDD,并利用其高效存儲結構提高不可靠節點的處理效率。在遍歷OBDD計算可靠度時,引入Hash表以避免對同一節點的重復訪問,從而減少冗余計算,進一步提高計算效率。在基準網絡中的對比實驗結果表明,該方法不僅能正確計算網絡可靠度,而且能快速分析大型網絡。

網絡可靠度;二元決策圖;不可靠節點;因子分解;布爾變量

1 概述

對于當前通信量急劇增加的骨干網絡[1-2]、廣泛應用的無線傳感器網絡以及災變環境下的數據網絡[3],節點失效帶來的網絡可靠性問題正被工程人員和學者廣泛關注[4-5]。對節點不可靠網絡進行可靠性分析時,需要解決2個問題:(1)如何處理不可靠節點[6];(2)當網絡規模較大時,如何提高計算效率[7-8]。文獻[3]應用因子分解來評估無線傳感器網絡的可靠度,該方法的計算開銷隨著網絡規模增大快速增長[9];文獻[10-11]應用分區等價類減少同構子網帶來的重復計算,大幅提高了網絡可靠度計算效率,但未考慮不可靠節點。文獻[12-13]提出應用二元決策圖(Binary Decision Diagram,BDD)計算節點不可靠網絡的可靠度,基于位向量的Hash表存儲開銷隨著網絡規模擴大快速增加。本文提出一種基于二元決策圖的節點不可靠網絡可靠度計算方法。首先按確定邊序分解網絡并生成節點可靠時的有序二元決策圖(Ordered BDD,OBDD),然后對OBDD變量節點執行邊替換操作,生成節點不可靠時網絡的OBDD,最后遍歷OBDD計算網絡可靠度。

2 符號表示

本文使用到的符號定義如下:

psrc:網絡的源端;

pdst:網絡的終端;

G(V,E):表示網絡拓撲結構的圖,其中,V是圖的點集,E是圖的邊集;

frel(G):網絡G的可靠度計算函數;

Oobdd(G):網絡G的OBDD結構;

fr_o(Oobdd(G)):根據網絡OBDD計算可靠度的函數;

G+e:收縮G中e邊生成的子網;

G-e:刪除G中e邊生成的子網。

此外:

(1)本文討論的可靠度是指網絡源端和終端之間保持連通的概率。源端和終端之間存在一條連通的路徑,則認為網絡可靠;否則,網絡不可靠。

(2)上述收縮和刪除邊的情形可擴展為:連續收縮邊a和b得到的子網表示為G+a+b;連續刪除邊a和b得到的子網表示為G-a-b;連續收縮邊a后刪除邊b得到的子網表示為G+a-b。

3 網絡可靠度計算方法

本文在計算效率和不可靠節點處理方面增強了基于OBDD的網絡可靠度計算方法:首先利用邊的因子分解創建節點可靠網絡的OBDD結構;其次根據邊和節點的邏輯聯系,對邊的OBDD變量節點執行邊替換操作,創建節點不可靠網絡的OBDD結構;最后遍歷OBDD來計算網絡可靠度,并利用Hash表減少對同一OBDD節點的重復訪問,進一步提高計算效率。

3.1 基于因子分解方法的OBDD創建

3.1.1 因子分解的基本概念

邊的因子分解方法通常假設網絡邊不可靠而節點可靠,根據邊的2種情況進行分解:邊可靠則收縮邊,把邊的2個端點合并成一個點;邊不可靠則刪除邊,把邊的2個端點保留在網絡中。基于因子分解的網絡可靠度計算可用如下公式表示[4]:

其中,e是網絡的某條邊;p是該邊可靠的概率;frel(G+e)是收縮e后網絡的可靠度;frel(G-e)是刪除e后網絡的可靠度。

圖1給出了利用邊的因子分解創建OBDD的實例,網絡G及其分解得到的子網按邊序e0～e5進行6次分解。其中,灰色點表示包含或者合并了源端(終端)的節點,圖中省略了源端和終端分離的子網,所有的分解過程最后聚焦為源端和終端合并為一個節點的子網。顯然,根據確定邊序執行因子分解把網絡逐層分為多個子網,每執行一次收縮邊和刪除邊操作就得到更小的子網。圖1中,除了第一次外的每次分解都是在上次分解得到的子網之上做進一步分解,得到更小的子網。圖中的實線表示收縮邊,虛線表示刪除邊,L6層的灰色點并為一點,表示源端和終端之間存在連通路徑。

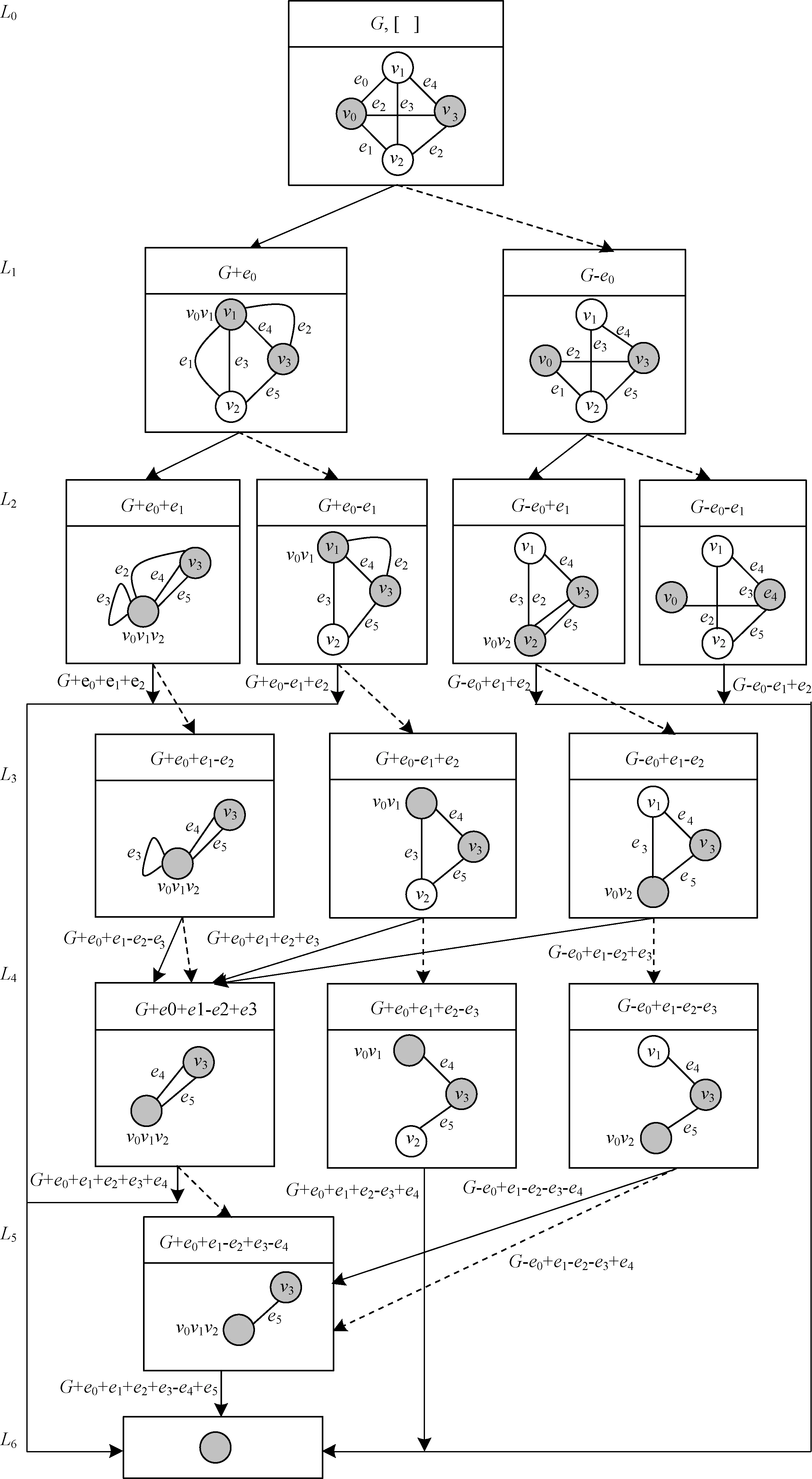
圖1 網絡的因子分解

3.1.2 節點可靠網絡的OBDD創建

創建 OBDD時,首先要確定邊序e0,e1,…,em-1,然后根據邊的邏輯(是否可靠)狀態來分析網絡是否連通。利用OBDD的ITE運算可以把每次分解對應的邏輯判斷記錄下來,最后得到描述整個網絡的狀態圖[7]。網絡G的OBDD結構可通過下式描述:

其中,f是邊序中某條邊的OBDD表達式;g是收縮邊得到子網的OBDD結構;h是刪除邊得到子網的OBDD結構。顯然,g和h需要對邊序中其他邊遞歸執行相同ITE運算得到。圖2給出了圖1中實例網絡的OBDD,創建OBDD的具體步驟可參考文獻[12-13]。

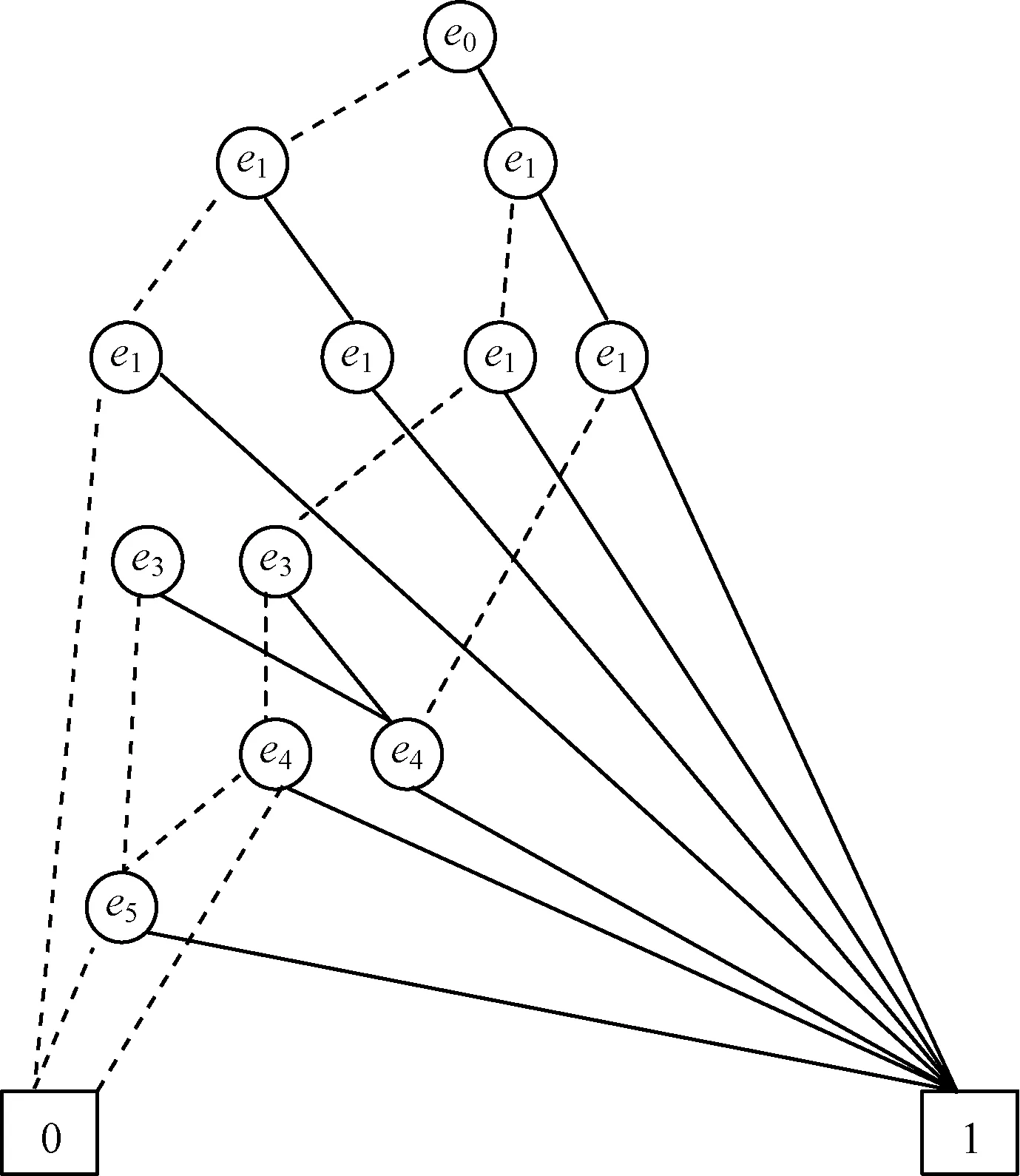
圖2 節點可靠網絡的OBDD

3.1.3 節點不可靠網絡的OBDD創建

前述OBDD創建過程假設網絡節點可靠,下文介紹一種應用邏輯運算處理不可靠節點的方法。

假設網絡G的節點可靠時,OBDD布爾變量Ve表示邊e,則G的OBDD結構可表示為:

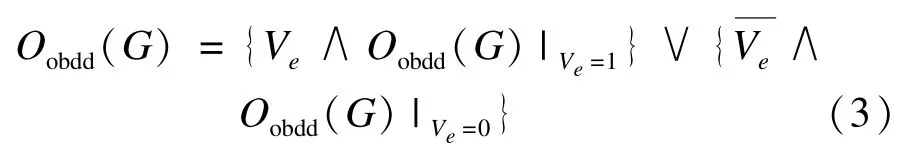
其中,Oobdd(G)|Ve=1表示e處于可靠狀態時G的OBDD結構;Oobdd(G)|Ve=0表示e處于不可靠狀態時G的OBDD結構。節點不可靠時需要考慮邊的2個端點的邏輯狀態,用布爾變量Va和Vb分別表示e的端點a,b。那么,e的完整布爾表示式為Va∧Ve∧Vb。為得到節點不可靠網絡G的OBDD,需要進行如下運算:

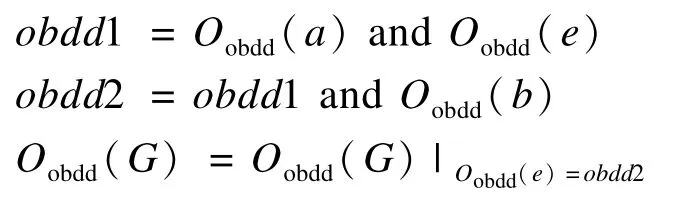
其中,obdd2是Va∧Ve∧Vb的OBDD結構。上述運算的含義是用端點不可靠的e替換OBDD中原有的e,執行了OBDD的composition運算[10]。本文將該運算過程稱為邊替換。

節點不可靠網絡的OBDD創建算法偽碼如下:

對圖2各邊執行下列邊替換操作后,得到圖3中節點不可靠時網絡的OBDD結構。

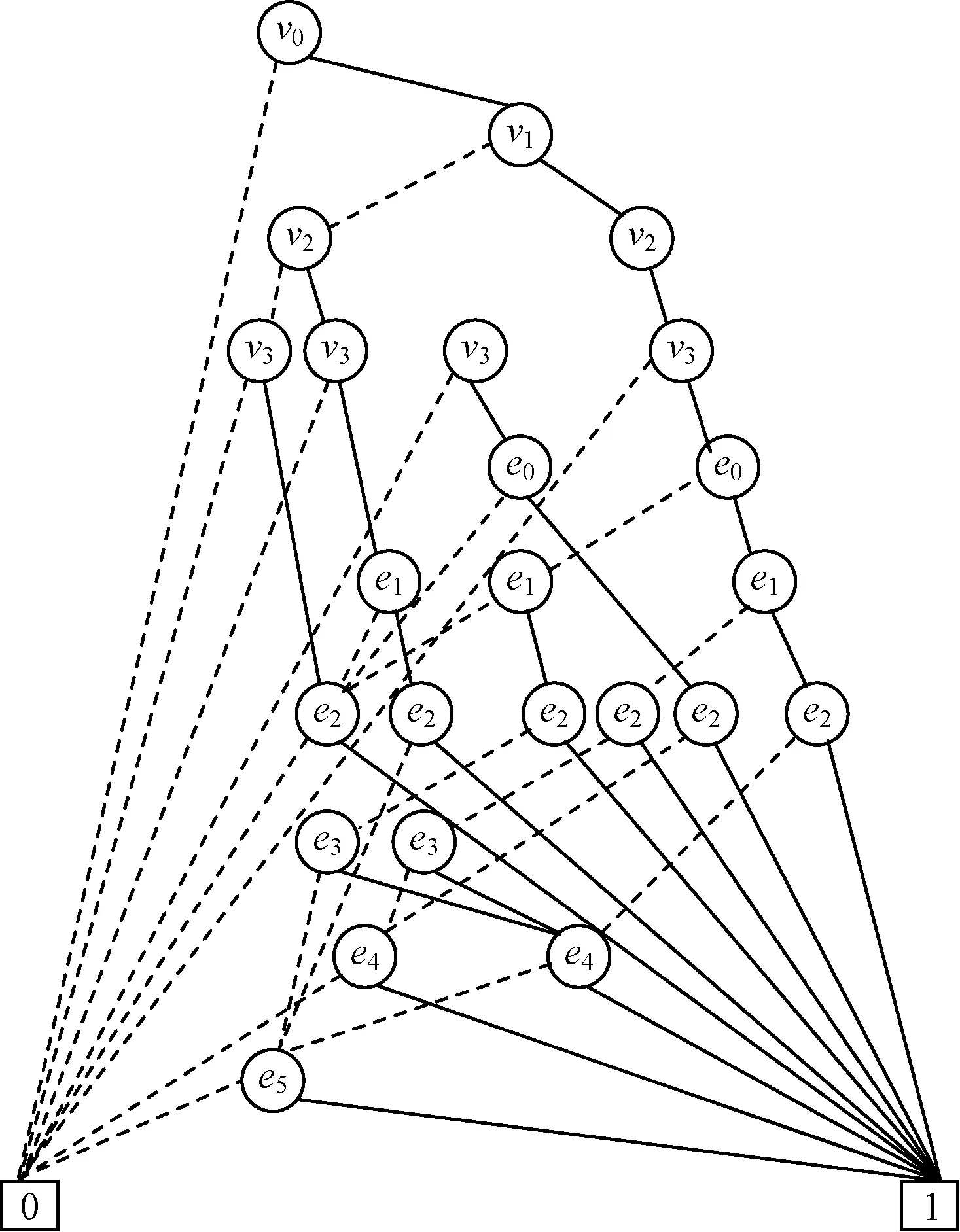
圖3 節點不可靠網絡的OBDD

(1)＜v0,e0,v1＞的布爾變量替代 ＜e0＞的變量:

(2)＜v0,e1,v2＞的布爾變量替代 ＜e1＞的變量:

(3)＜v0,e2,v3＞的布爾變量替代 ＜e2＞的變量:

(4)＜v1,e3,v2＞的布爾變量替代 ＜e3＞的變量:

(5)＜v1,e4,v3＞的布爾變量替代 ＜e4＞的變量:

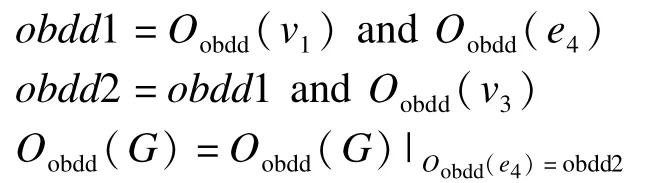
(6)＜v2,e5,v3＞的布爾變量替代 ＜e5＞的變量:

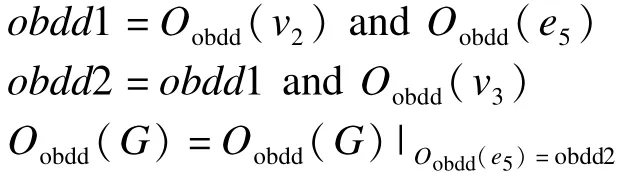
3.2 可靠度計算

3.2.1 可靠度計算原理及算法

按照上述改進方法創建網絡G的OBDD結構后,可通過下面的遞歸公式來計算網絡G的可靠度:

其中,0≤k＜n;Oobdd(G)|xk=1是xk=1時網絡G的OBDD,即xk對應節點或邊可靠時G的OBDD結構;Oobdd(G)|xk=0是xk=0時網絡G的OBDD結構,即xk對應節點或邊不可靠時G的 OBDD結構; Pr(xk=1)是xk對應節點或邊的可靠概率,Pr(xk=0)是xk對應節點或邊不可靠概率;bddtrue和bddfalse分別表示OBDD結構中的邏輯真和邏輯假;k的初始值為0。顯然,完成上述公式的計算需要沿OBDD結構遍歷其節點,而且某些節點被多次訪問。在圖4中,e2,e4和e5在計算過程中被多次訪問,從而帶來重復計算。為減少這種冗余計算,設計算法時建立一個hash表,以當前子網的OBDD根節點標號為索引記錄當前子網的可靠度數值,當再次訪問該節點時直接返回已保存的數值。

下面的NetRel_urn()給出了節點不可靠網絡的可靠度計算偽碼。其中,G代 表 網 絡; BDDConstruct()是因子分解創建節點可靠網絡OBDD的算法,詳細實現可參考文獻[4]; BDDConstruct_urn()是上文創建節點不可靠網絡的OBDD算法;BDDRel()是本小節上述計算方法的實現。

3.2.2 算法復雜度分析

本文算法由三部分組成:BDDConstruct, BDDConstruct_urn和BDDRel。其復雜度由其計算復雜度決定。文獻[9]通過優化節點可靠網絡的分解過程,給出BDDConstruct和BDDRel復雜度的上界:

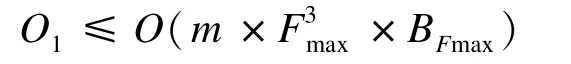
其中,O1為BDDConstruct和BDDRel的算法復雜度,m為網絡的邊數,Fmax為最大邊界集的元素個數,BFmax是最大邊界集的Bell數。這個值是現有研究中比較實用的上界值,本文按文獻[9]的方法優化網絡分解后,BDDConstruct_urn的復雜度就可由BDD寬度和深度計算。BDD深度由網絡的邊數確定,BDD寬度上界可根據文獻[9]確定:

其中,Wbdd是 BDD 寬度上界。由算法結構, BDDConstruct_urn的復雜度上界為:

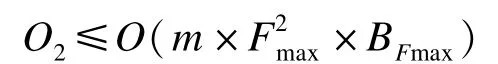
綜上所述,整個算法復雜度的上界為:

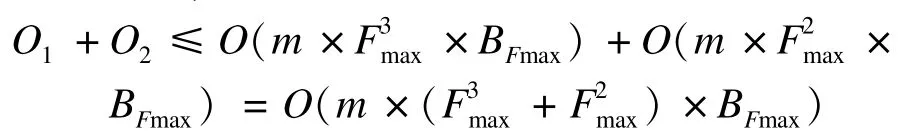
可見,Fmax決定了算法的復雜度,數百節點的網絡一般都有較小的Fmax值。根據文獻[9]優化后,本文算法的計算效率將得到進一步改善。

4 實驗與結果分析

本文采用Buddy版BDD實現本文方法,并將其C語言實現程序命名為NetRel_urn[14]。為方便對比分析,同時實現了文獻[3,13]的方法,并分別命名為NetRel_yz和NetRel_x。實驗計算機的CPU工作頻率為2.4 GHz,內存容量為2 GB,操作系統為2.6內核的紅帽Linux。圖4列出的9個網絡被較多文獻使用[9-13],因此,本文將其作為基準網絡來檢驗計算的正確性和效率。網絡中的黑實點分別表示源端和終端,點和邊可靠度是0.9。

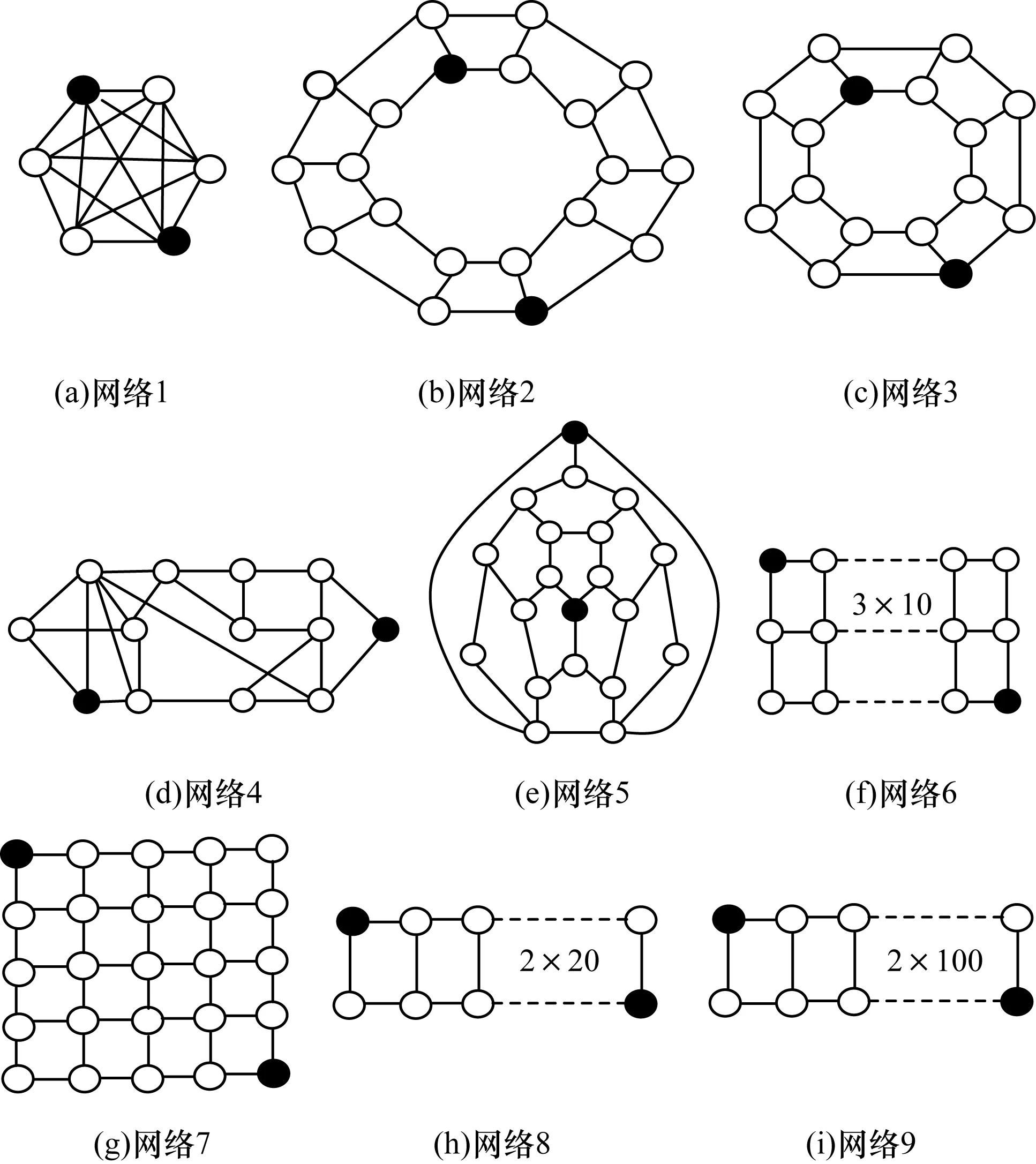
圖4 實驗基準網絡

實驗結果如表1所示,其中,“-”表示開銷超過1 h。

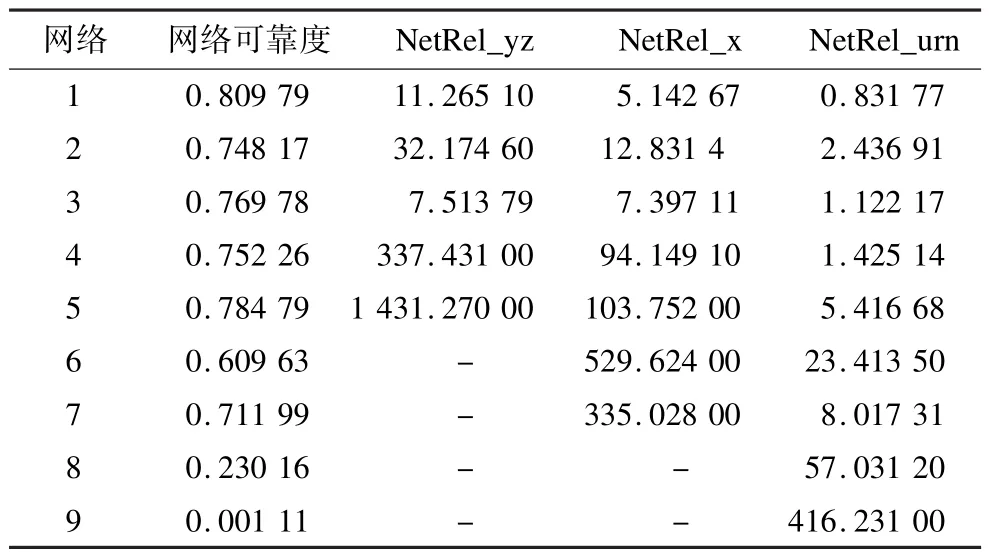
表1 計算時間比較 s

每個程序被執行10次后,其平均計算時間被記錄為表中的時間開銷。可以看出,NetRel_yz和NetRel_ x的開銷高于NetRel_urn。從網絡6、網絡7、網絡8和網絡9的計算結果可以發現:隨著網絡規模增大, NetRel_yz的計算開銷顯著上升,甚至在1 h內也無法得到計算結果;NetRel_x也無法計算網絡8和網絡9的可靠度;相比之下,NetRel_urn完成了計算任務。實驗結果表明,本文方法可有效評估節點不可靠網絡的可靠度,當網絡規模較大時,其計算開銷較低。

5 結束語

為高效處理不可靠節點,本文提出了一種網絡可靠度計算方法,利用OBDD變量節點的邊替換操作和OBDD高效存儲結構提高計算效率。實驗結果表明,該方法能以較快的速度計算規模較大網絡的可靠度。但本文未考慮節點和邊失效的統計相關性,下一步將對其進行深入研究。

[1] Ball M,Thomas M.Hand Books in Operations Research andManagementScience,NetworkModels[M]. [S.l.]:Elsevier,1995.

[2] Lin Y K,Chang P C.A Novel Reliability Evaluation Technique for Stochastic-flow Manufacturing Networks with Multiple Production Lines[J].IEEE Transactions on Reliability,2013,62(1):92-104.

[3] AboElFotoh H M F,IyengarS S,Chakrabarty K. Computing Reliability and message delay for cooperative Wireless Distributed Sensor Networks Subject to Random Failures[J].IEEE Transactions on Reliability, 2005,54(1):145-155.

[4] 肖宇峰.基于離散概率模型的二端網絡可靠性分析[D].北京:北京郵電大學,2009.

[5] 江逸楠,李瑞瑩,黃 寧,等.網絡可靠性評估方法綜述[J].計算機科學,2012,39(5):9-13.

[6] 吳 俊,段東立,趙 娟.網絡系統可靠性研究現狀與展望[J].復雜系統與復雜性科學,2011,8(2):77-86.

[7] 肖宇峰,李 昕,李玉宏,等.用改進的OBDD方法計算通信網可靠度[J].計算機應用研究,2010,27(3):114-117.

[8] Huang N,Chen Y,Hou D,et al.Application Reliability for Communication Networks and Its Analysis Method[J].Journal of Systems Engineering and Electronics,2011,22(6):1030-1036.

[9] Hardy G,LucetC,LimniosN.K-terminalNetwork Reliability Measures with Binary Decision Diagrams[J]. IEEE Transactions on Reliability,2007,56(3):506-515.

[10] Imai H,Sekine K,Imai K.Computational Investigations of all-terminal Network Reliability via BDDs[J].IEICE Transactions on Fundamentals,1999,E82-A(5):714-721.

[11] Carlier J,Lucet C.A Decomposition Algorithm for Network Reliability Evaluation[J].Discrete Applied Mathematics,1996,65(1):141-156.

[12] Kuo S Y,Yeh F M,Lin H Y.Efficient and Exact Reliability Evaluation for Networks with Imperfect Vertices[J].IEEE Transactions on Reliability,2007,56 (2):198-211.

[13] Xing Liudong.An Efficient Binary Decision Diagram Based Approach for Network Reliability and Sensitivity Analysis[J].IEEE Transactions on Systems,Man,and Cybernetics——Part A:Systems and Humans,2008,38 (6):105-115.

[14] Andersen H.An Introduction to Binary Decision Diagrams[M].[S.l.]:Elsevier,1997.

編輯 金胡考

Reliability Computation of Network with Unreliable Nodes Based on Binary Decision Diagram

XIAO Yufenga,b,ZHANG Huaa,b
(a.Information Engineering School;b.Special Environment Robot Technology Key Laboratory of Sichuan Province,Southwest University of Science and Technology,Mianyang 621010,China)

According to the inefficient reliability computation of network with unreliable nodes,this paper proposes a network reliability computation method based on Binary Decision Diagram(BDD).After the Ordered Binary Decision Diagram(OBDD)construction with factoring theorem,this method executes the edge replacements to OBDD variables of edges with the relation between nodes and edges,and the OBDD of network with unreliable nodes is constructed.Based on efficient OBDD structure,the computations about unreliable nodes are improved.Furthermore,a hash table is used to avoid the repeated access to same node when the reliability is calculated with OBDD traversal.Therefore,the redundant calculations are reduced,and the reliability computation efficiency of network with unreliable nodes is enhanced. Experiments are arranged on benchmark networks,and data analysis shows that this method can accurately calculate network reliability and quickly analyze some large networks.

network reliability;Binary Decision Diagram(BDD);unreliable node;factoring;Boolean variable

1000-3428(2015)01-0087-05

A

TP393

10.3969/j.issn.1000-3428.2015.01.016

國家核能開發科研基金資助項目([2011]1137);四川省科技支撐計劃基金資助項目(2013GZX0152);四川省教育廳基金資助重點項目(14ZA0091)。

肖宇峰(1978-),男,副研究員、博士,主研方向:網絡通信,計算機系統可靠性評估;張 華,教授、博士。

2014-01-20

2014-03-20 E-mail:xiaoyf_swit1@163.com

中文引用格式:肖宇峰,張 華.基于二元決策圖的節點不可靠網絡可靠度計算[J].計算機工程,2015,41(1):87-91.

英文引用格式:Xiao Yufeng,Zhang Hua.Reliability Computation of Network with Unreliable Nodes Based on Binary Decision Diagram[J].Computer Engineering,2015,41(1):87-91.