受限模糊網(wǎng)絡(luò)可信近鄰查詢

高 峻,郝忠孝,2

(1.哈爾濱理工大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院,哈爾濱150080;2.哈爾濱工業(yè)大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院,哈爾濱150001)

受限模糊網(wǎng)絡(luò)可信近鄰查詢

高 峻1,郝忠孝1,2

(1.哈爾濱理工大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院,哈爾濱150080;2.哈爾濱工業(yè)大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院,哈爾濱150001)

針對(duì)不確定網(wǎng)絡(luò)環(huán)境下的近鄰查詢問題,給出一種新的解決方法。將不確定網(wǎng)絡(luò)建模為模糊圖,定義模糊圖中兩點(diǎn)間的可信最短路徑距離和可信最短路徑期望距離,在可信距離基礎(chǔ)上,提出模糊圖可信近鄰查詢概念,并給出網(wǎng)絡(luò)距離受限條件下的模糊圖可信近鄰查詢算法和即時(shí)可信近鄰查詢算法。算法采用模糊模擬方法降低問題難度,使用網(wǎng)絡(luò)距離約束縮小搜索空間,運(yùn)用優(yōu)先隊(duì)列快速得到滿足精度ε要求的可信近鄰查詢結(jié)果。算法的時(shí)間復(fù)雜度分別為O((2r+Δr)(e+nlgn)+hlgh+lgn)和O(e+(n+1)lgn)。理論分析與實(shí)驗(yàn)結(jié)果表明,可信近鄰查詢算法能夠從模糊角度解決不確定網(wǎng)絡(luò)環(huán)境下的近鄰查詢問題。

不確定網(wǎng)絡(luò);模糊圖;可信距離;可信近鄰;模糊模擬;距離約束

1 概述

不確定性數(shù)據(jù)處理是數(shù)據(jù)庫(kù)查詢領(lǐng)域的研究熱點(diǎn),目前已取得很多成果,但這些研究多集中在實(shí)體數(shù)據(jù)的不確定性,在現(xiàn)實(shí)中覆蓋還不夠全面。現(xiàn)實(shí)中存在實(shí)體間關(guān)系的不確定性,如路網(wǎng)結(jié)點(diǎn)間路徑有時(shí)關(guān)閉,有時(shí)開放,多數(shù)是根據(jù)車流量而變化的介于關(guān)閉和開放間的一個(gè)不確定量,這時(shí)根據(jù)結(jié)點(diǎn)間最短路徑距離得到的最近鄰查詢結(jié)果并不能保證是最有效近鄰。這就需要考慮在不確定網(wǎng)絡(luò)環(huán)境下的近鄰查詢問題。

對(duì)于實(shí)體數(shù)據(jù)的不確定性處理,已有很多好的方法,如文獻(xiàn)[1]給出SQL查詢方法,文獻(xiàn)[2]給出一種索引方法,文獻(xiàn)[3-4]給出k-近鄰查詢方法,文獻(xiàn)[5]給出一種范圍查詢分析方法。但這些方法并不能直接用于實(shí)體間關(guān)系的不確定性處理。

已有文獻(xiàn)關(guān)注這個(gè)問題,其中,文獻(xiàn)[6]分析了社會(huì)網(wǎng)絡(luò)環(huán)境的不確定性、查詢需求并給出處理方法。文獻(xiàn)[7]給出了移動(dòng)網(wǎng)絡(luò)環(huán)境使用k近鄰查詢解決概率路徑問題的方法。文獻(xiàn)[8]表明生物網(wǎng)絡(luò)環(huán)境也有這樣的查詢需求。文獻(xiàn)[9]使用隨機(jī)理論給出了不確定網(wǎng)絡(luò)環(huán)境下近鄰查詢處理方法。將不確定網(wǎng)絡(luò)環(huán)境建模為概率加權(quán)圖,實(shí)體間關(guān)系的不確定性用固定概率值表示,定義了概率加權(quán)圖中結(jié)點(diǎn)間各種距離,并基于這些距離進(jìn)行近鄰查詢。這些工作都將實(shí)體間關(guān)系的不確定性建模為概率性,但現(xiàn)實(shí)中實(shí)體間關(guān)系的不確定性有時(shí)還表現(xiàn)為模糊性,如路網(wǎng)結(jié)點(diǎn)間的暢通程度。

模糊集理論是處理不確定性問題的有力工具,已被廣泛用于數(shù)據(jù)類型[10]和運(yùn)算定義[11]以及空間查詢[12]等領(lǐng)域。本文將探討使用模糊集理論來處理不確定網(wǎng)絡(luò)環(huán)境下的近鄰查詢問題。

2 相關(guān)概念

模糊集理論在許多實(shí)際領(lǐng)域已得到應(yīng)用。為了度量模糊事件,文獻(xiàn)[13]提出了可能性測(cè)度,文獻(xiàn)[14]提出了必要性測(cè)度,之后文獻(xiàn)[15]提出了可信性測(cè)度。可信性測(cè)度被認(rèn)為是與概率論中的概率測(cè)度平行的概念。

定義1(模糊網(wǎng)絡(luò)) 模糊網(wǎng)絡(luò)是指在模糊集理論框架下討論的不確定網(wǎng)絡(luò),即網(wǎng)絡(luò)實(shí)體確定而實(shí)體間關(guān)系的不確定表現(xiàn)為實(shí)體間關(guān)系的模糊性。

將模糊網(wǎng)絡(luò)建模為圖,網(wǎng)絡(luò)實(shí)體表示為圖中結(jié)點(diǎn),實(shí)體間關(guān)系表示為圖中邊,實(shí)體間關(guān)系是模糊的,則得到模糊圖,圖中邊給出可信值,表示邊存在的可信度,即實(shí)體間關(guān)系的可信度。模糊圖與普通圖類似,可分為有向圖與無向圖,加權(quán)圖與無權(quán)圖。這里討論的是無向加權(quán)模糊圖。下面給出模糊圖的形式定義。

定義2(模糊圖) 設(shè)=(V,E,W,Cr)表示模糊圖,其中,V表示圖的結(jié)點(diǎn)集;E表示圖的邊集;W表示邊的權(quán)重集;Cr表示邊存在的可信度集。w(e)表示邊e的權(quán)重,cr(e)表示邊e存在的可信度。cr(e)＞0,當(dāng)且僅當(dāng)e∈E。

圖1為模糊圖示例。

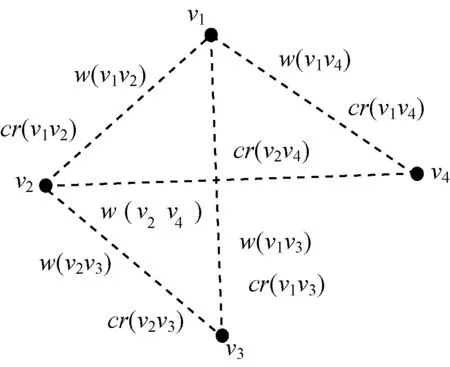
圖1 模糊圖示例

設(shè)模糊圖=(V,E,W,Cr),其中,V={v1,v2,v3,v4},E={v1v2,v1v3,v1v4,v2v3,v2v4},W={w(v1v2),w(v1v3),w(v1v4),w(v2v3),w(v2v4)},Cr={cr(v1v2),cr(v1v3),cr(v1v4),cr(v2v3),cr(v2v4)}。

定義3(樣本圖) 已知模糊圖=(V,E,W,Cr),樣本圖G是模糊圖的一個(gè)實(shí)例,EG為G的邊集,則其可信度cr(G)=

圖2是圖1所示模糊圖的樣本圖示例,其中,圖2(a)為樣本圖G1,EG1={v1v2,v1v4,v2v3},G1的可信度為cr(G)=cr(v1v2)×cr(v1v4)×cr(v2v3)=0.3×0.7×0.6=0.125。

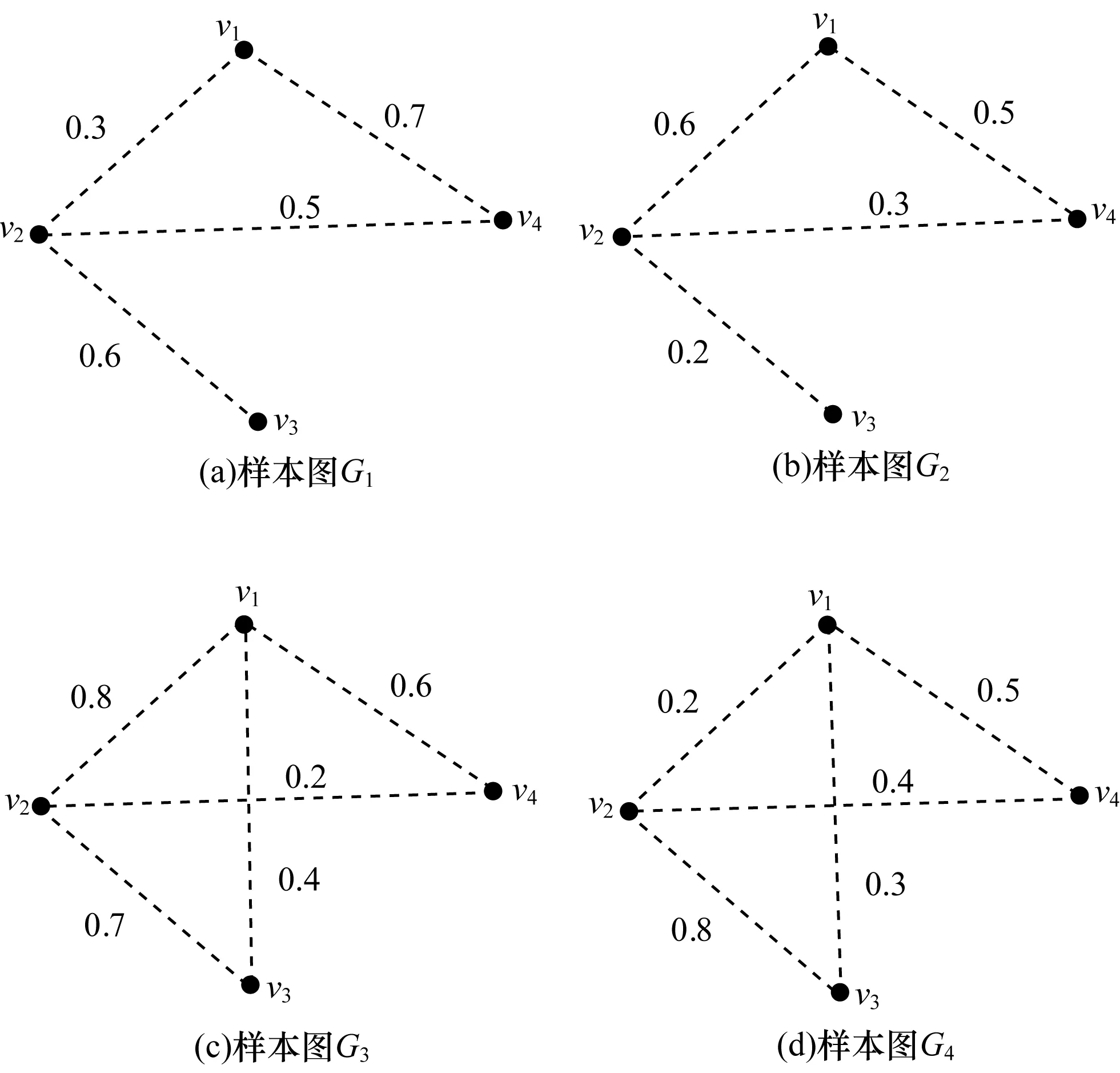
圖2 樣本圖示例

設(shè)模糊圖=(V,E,W,Cr),G是的樣本圖,vi,vj∈V,將圖中兩點(diǎn)間的最小權(quán)重表達(dá)為兩點(diǎn)間的最短路徑距離。

定義4樣本圖中兩點(diǎn)間最短路徑距離:dG(vi,vj)=d表示vi,vj在G中最短路徑距離為d,Ed為G中vi,vj間最短路徑邊集,dG(vi,vj)為d的可信度cr(dG(vi,vj)=d)=

在圖2(a)所示樣本圖G1中,設(shè)v1,v2和v2,v3間距離均為1,則v1,v3間最短路徑距離dG1(v1,v3)=2,其邊集E2={v1v2,v2v3},dG1(v1,v3)=2的可信度為:

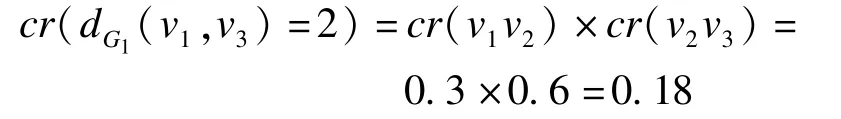
在圖2(b)所示樣本圖G2中,設(shè)v1,v2和v2,v3間距離均為1,則v1,v3間最短路徑距離dG2(v1,v3)=2,其邊集E2={v1v2,v2v3},dG2(v1,v3)=2的可信度為:

在圖2(c)所示樣本圖G3中,設(shè)v1和v3間距離為1,則v1,v3間最短路徑距離dG3(v1,v3)=1,其邊集E1={v1v3},dG3(v1,v3)=1的可信度為:

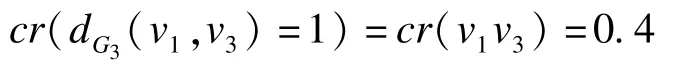
在圖2(d)所示樣本圖G4中,設(shè)v1和v3間距離為1,則v1,v3間最短路徑距離dG(v1,v3)=1,其邊集E1={v1v3},dG4(v1,v3)=1的可信度為:

定義5模糊圖中兩點(diǎn)間最短路徑距離:模糊圖中vi,vj間最短路徑距離記為d(vi,vj),d(vi,vj)為d的可信度為:

設(shè)圖2所示為模糊圖的所有樣本圖,其中滿足v1,v3間最短路徑距離dG(v1,v3)=2的樣本圖為圖2(a)、圖2(b),則模糊圖中v1,v3間最短路徑距離d(v1,v3)=2的可信度為:

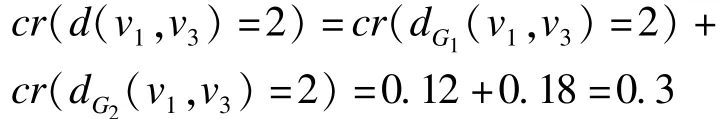
滿足v1,v3間最短路徑距離dG(v1,v3)=1的樣本圖為(c)(d),則模糊圖中v1,v3間最短路徑距離d(v1,v3)=1的可信度為:

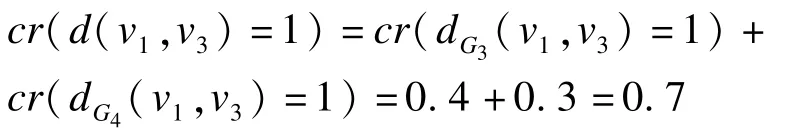
定義6可信最短路徑距離:vi,vj間可信最短路徑距離

根據(jù)上述假設(shè)與計(jì)算可知,圖1所示模糊圖中v1,v3間可信最短路徑距離為:

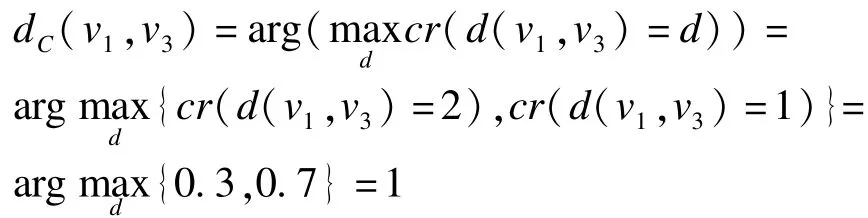
定義7可信最短路徑期望距離:vi,vj間可信最短路徑期望距離

在圖1所示模糊圖中,v1,v3間最短路徑期望距離為:

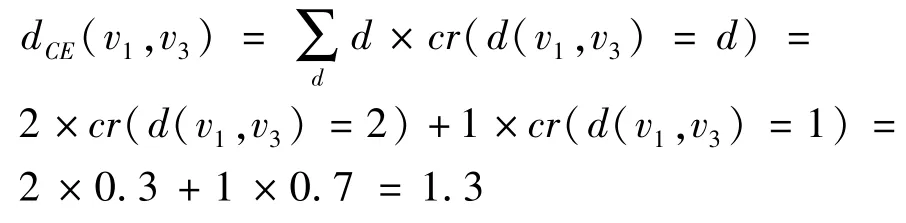
3 模糊圖的存儲(chǔ)方法

模糊圖=(V,E,W,Cr)中的V,E,W相對(duì)穩(wěn)定,而Cr則變化較大,因此在存儲(chǔ)時(shí)分開存儲(chǔ),用指針相連。使用鄰接表對(duì)模糊圖進(jìn)行表示。模糊圖=(V,E,W,Cr)的鄰接表表示由一個(gè)包含|V|個(gè)列表的數(shù)組所組成,其中每個(gè)列表對(duì)應(yīng)于V中的一個(gè)頂點(diǎn)。對(duì)于每一個(gè)vi∈V,鄰接表li包含所有滿足條件vivj∈V的結(jié)點(diǎn)vj。鄰接表形式為li:＜vj,w(vivj),pt1,pt2,next＞。其中,li表示結(jié)點(diǎn)vi的鄰接表;vj表示vi的鄰接點(diǎn);w(vivj)表示vivj的權(quán)重,在圖中簡(jiǎn)記為wij;pt1為指向vivj具體抽象數(shù)據(jù)類型所在頁(yè)指針,而抽象數(shù)據(jù)類型的前后分別設(shè)置指針指向結(jié)點(diǎn)鄰接表所在頁(yè);pt2為指向鄰接表中動(dòng)態(tài)部分存儲(chǔ)位置的指針,其存儲(chǔ)格式為三元數(shù)組,數(shù)組第一個(gè)位置表示樣本圖號(hào),數(shù)組第2個(gè)位置表示vj和vi在樣本圖中是否鄰接的邏輯值,若在樣本圖中兩結(jié)點(diǎn)鄰接,則邏輯值為1,否則邏輯值為0,數(shù)組第3個(gè)位置表示vivj在樣本圖中的可信度。next[vj]為指向vj的后繼元素指針,若next[vj]指向null,則vj沒有后繼元素,它是尾。

圖1、圖2所示的模糊圖的樣本圖的表示形式如圖3所示。

圖3 模糊圖的表示形式

以結(jié)點(diǎn)v1為例。v1有3個(gè)鄰接點(diǎn)v2,v3和v4,則其鄰接表l1包括形式相同的3項(xiàng)。以第一項(xiàng)為例,其形式為＜v2,w12,p5,p7,next＞,其中,v2是v1的鄰接點(diǎn);w12表示v1v2的權(quán)重;p5為邊v1v2的具體抽象數(shù)據(jù)類型所在頁(yè),而v1v2的具體抽象數(shù)據(jù)類型的前后的p1和p2分別為結(jié)點(diǎn)v1和v2的鄰接表所在頁(yè);p7為邊v1v2的動(dòng)態(tài)信息所在頁(yè),next[v2]指向后繼元素v3。p7中第一行＜1,1,0.3＞為樣本圖G1中v1v2的動(dòng)態(tài)信息,第一位置的1表示樣本圖為G1,第二位置的1表示在樣本圖G1中v1v2連接,第三位置的0.3表示在樣本圖G1中v1v2連接的可信度,其他行同理,分別表示樣本圖G2,G3和G4中v1v2的動(dòng)態(tài)信息。

給定一個(gè)新的結(jié)點(diǎn)vk,不妨設(shè)其鄰接點(diǎn)為vi…vj,過程Adjacent-insert將vk加入到鄰接表中。

Adjacent-insert(L,vk):

(1)建立vk鄰接表lk,包含項(xiàng)＜vi,wki,p?,p?,next＞…＜vj,wkj,p?,p?,next＞;

(2)對(duì)鄰接表li…li,增加項(xiàng) ＜vk,wk?,p?,p?,next＞,原尾部指針指向新加項(xiàng),而next[vk]指向null;

給定一個(gè)已有結(jié)點(diǎn)vk,不妨設(shè)其鄰接點(diǎn)為vi…vj,過程Adjacent-delete將從鄰接表中刪除vk。

Adjacent-delete(L,vk):

(1)刪除vk鄰接表lk;

(2)在鄰接表li…li中,若項(xiàng)＜vk,wk?,p?,p?,next＞位于鄰接表頭部,則直接刪除;若其位于鄰接表中部,則將其前序結(jié)點(diǎn)的next指針指向其后繼結(jié)點(diǎn),刪除此項(xiàng);若其位于鄰接表尾部,則將其前序結(jié)點(diǎn)的next指針指向null,刪除此項(xiàng)。

4 可信距離計(jì)算

模糊圖中可信距離的精確計(jì)算代價(jià)較高,需在所有可能樣本圖中計(jì)算點(diǎn)間的最短路徑距離和點(diǎn)間路徑存在的可信度,復(fù)雜度達(dá)到指數(shù)級(jí)。這里使用對(duì)模糊系統(tǒng)進(jìn)行抽樣實(shí)驗(yàn)的模糊模擬技術(shù)進(jìn)行近似計(jì)算。模糊模擬技術(shù)沒有隨機(jī)模擬技術(shù)成熟,沒有大數(shù)定理來保證抽樣結(jié)果的精確度,但可將模糊理論與模糊模擬結(jié)合使用來得到滿意的近似值。

定義8設(shè)ξ1,ξ2,…,ξr是獨(dú)立同分布的模糊變量,有相同有限期望值。若ε}=0,則稱模糊變量序列{ξi}依可信性收斂到 ξ[16]。

定義9設(shè)ξ1,ξ2,…,ξr是獨(dú)立同分布的模糊變量,有相同有限期望值。若,則稱模糊變量序列{ξi}依均值收斂到ξ[16]。

4.1 可信最短路徑距離計(jì)算

根據(jù)定義8可通過過程Compute-dC(q,v)得到可信最短路徑距離的近似值。

Compute-dC(q,v):

(1)在模糊圖中均勻抽取r個(gè)樣本,計(jì)算每個(gè)樣本圖中vi,vj兩點(diǎn)間最短路徑距離d及其可信度,得到模糊圖中vi,vj兩點(diǎn)間最短路徑距離為d的近似可信度:

(2)在模糊圖中均勻抽取r+Δr個(gè)樣本,計(jì)算每個(gè)樣本圖中vi,vj兩點(diǎn)間最短路徑距離d及其可信度,得到模糊圖中vi,vj兩點(diǎn)間最短路徑距離為d的近似可信度:

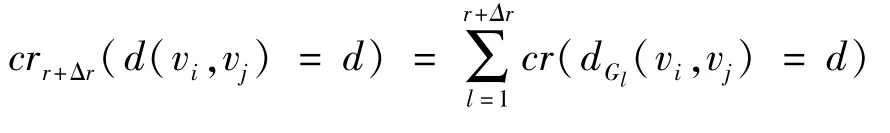
(3)若對(duì)精度ε＞0

|crr+Δr(d(vi,vj)=d)-crr(d(vi,vj)=d)|≤ε

則crr+Δr(d(vi,vj)=d)即作為模糊圖中vi,vj兩點(diǎn)間最短路徑距離為d的近似可信度。否則令r=r+Δr,轉(zhuǎn)(2)。

(4)比較vi,vj兩點(diǎn)間最短路徑距離的近似可信度,其中使近似可信度最大的d值即為vi,vj兩點(diǎn)間可信最短路徑距離dC(q,v)的近似值。

定理1設(shè)模糊圖中兩點(diǎn)間最短路徑距離的可信度是收斂的,則對(duì)任意ε＞0,當(dāng)r→∞時(shí),有:

在模糊模擬理論中,因模糊變量收斂,所以模擬結(jié)果應(yīng)與其極限值接近,但其極限值無法實(shí)際得到,因此使用兩次模擬結(jié)果的差值來作為模擬結(jié)束的條件。

根據(jù)定理1和模糊模擬理論可知,若對(duì)任意ε＞0,|crr+Δr(d(vi,vj)=d)-crr(d(vi,vj)=d)|≤ε,則crr+Δr(d(vi,vj)=d)即可作為模糊圖中vi,vj兩點(diǎn)間最短路徑距離為d的精度為ε的近似可信度。

假設(shè)模糊圖的基圖結(jié)點(diǎn)數(shù)為n,邊數(shù)為e。抽取r個(gè)樣本,每個(gè)樣本圖中,vi,vj兩點(diǎn)間最短路徑距離的計(jì)算使用 Dijkstra算法,時(shí)間復(fù)雜度為O(e+nlgn),計(jì)算模糊圖中vi,vj兩點(diǎn)間最短路徑距離為d的近似可信度的時(shí)間復(fù)雜度為r,即第一步的時(shí)間復(fù)雜度為O(r(e+nlgn)),第2步同理,時(shí)間復(fù)雜度為O((r+Δr)(e+nlgn)),第3步時(shí)間復(fù)雜度為常數(shù),第4步若設(shè)vi,vj兩點(diǎn)間最短路徑距離的可能值有h個(gè),則其時(shí)間復(fù)雜度O(hlgh)),即可信最短路徑距離計(jì)算的時(shí)間復(fù)雜度為O((2r+Δr)(e+nlgn)+hlgh)。

4.2 可信最短路徑期望距離計(jì)算

根據(jù)定義9可通過過程Compute-dCE(q,v)得到可信最短路徑期望距離的近似值。過程 ComputedCE(q,v)與Compute-dC(q,v)類似。

定理2設(shè)模糊圖中兩點(diǎn)間可信最短路徑期望距離是收斂的,則對(duì)ε＞0,當(dāng)r→∞時(shí),有:

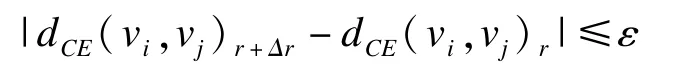
定理2的證明與定理1的證明類似。同理,若對(duì)任意ε＞0,有|dCE(vi,vj)r+Δr-dCE(vi,vj)r|≤ε,則dCE(vi,vj)r+Δr即可作為模糊圖中vi,vj兩點(diǎn)間可信最短路徑期望距離的精度為ε的近似值。

可信最短路徑期望距離計(jì)算的時(shí)間復(fù)雜度也為O((2r+Δr)(e+nlgn)+hlgh)。這個(gè)關(guān)于結(jié)點(diǎn)數(shù)和邊數(shù)的多項(xiàng)式近似解法比精確指數(shù)解法可行,且精度可以根據(jù)需要調(diào)節(jié)。

5 可信近鄰查詢

定義10可信k近鄰查詢:已知模糊圖=(V,E,W,Cr),查詢對(duì)象q∈V,可信k近鄰查詢給出與q的可信最短路徑距離(或可信最短路徑期望距離)最小的V中k個(gè)對(duì)象,即對(duì)?v∈V,有:

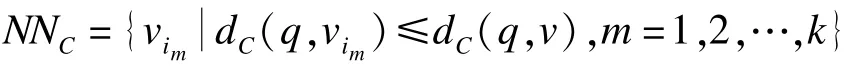
近鄰查詢是要找到與查詢對(duì)象距離較近的目標(biāo)對(duì)象,若結(jié)果與查詢對(duì)象距離較遠(yuǎn),則失去意義,因此這里僅考慮距離受限的近鄰查詢,從而縮小搜索空間。

算法思想:算法中設(shè)置了一結(jié)點(diǎn)集NNC,從查詢點(diǎn)q到NNC中結(jié)點(diǎn)的可信最短路徑距離均已確定。算法反復(fù)計(jì)算訪問結(jié)點(diǎn)v與查詢點(diǎn)q的可信最短路徑距離,若小于NNC中結(jié)點(diǎn)的可信最短路徑距離,則將v加入NNC中。

以可信最短路徑距離為基礎(chǔ)的可信k近鄰查詢算法描述如算法1所示。

算法1可信k近鄰查詢算法

輸入模糊圖=(V,E,W,Cr),查詢點(diǎn)q∈V,樣本數(shù)初值r,樣本數(shù)增量Δr,近鄰數(shù)k,距離約束D,精度ε

輸出k-NN查詢結(jié)果集NNC

定理3模糊圖=(V,E,W,Cr),查詢點(diǎn)q∈V。對(duì)該圖運(yùn)行可信k近鄰查詢算法,則在算法終止時(shí),對(duì)在距離約束D范圍內(nèi)的所有v∈V,有:

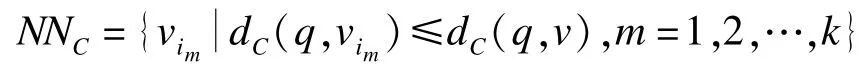
證明:初始化:初始時(shí),NNC為空集,顯然成立。

保持:dC-max為NNC中結(jié)點(diǎn)與q的最大可信最短路徑距離,當(dāng)NNC為空集時(shí),dC-max為無窮大。NNC中元素個(gè)數(shù)未達(dá)到k個(gè)時(shí),則將v直接加入NNC,否則比較v與q的dC(q,v)和dC-max。若小于dC-max,則放入NNC,大于dC-max,則舍去。這就使NNC中結(jié)點(diǎn)是當(dāng)前已訪問結(jié)點(diǎn)中與查詢點(diǎn)q可信最短路徑距離最小的k個(gè)結(jié)點(diǎn)。

終止:在終止時(shí),所有與q的距離小于預(yù)先給定距離D的結(jié)點(diǎn),均已訪問,且與dC-max比較完畢。因此,對(duì)在距離約束D范圍內(nèi)的所有v∈V,有:

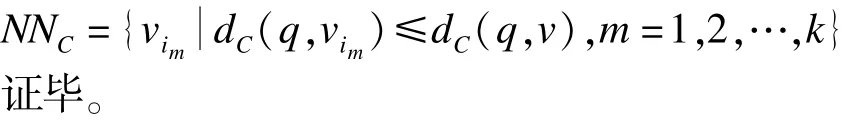
算法分析:算法1中的步驟(4)～步驟(6)是每個(gè)訪問結(jié)點(diǎn)與查詢點(diǎn)p的可信最短路徑距離及其可信度的計(jì)算過程,其復(fù)雜度為O((2r+Δr)(e+nlgn)+hlgh),步驟(7)～步驟(9)是利用優(yōu)先隊(duì)列找到k個(gè)近鄰,其時(shí)間復(fù)雜度最壞為O(lg(n)),即算法1的時(shí)間復(fù)雜度為O((2r+Δr)(e+nlgn)+hlgh+lgn)。

以可信最短路徑期望距離為基礎(chǔ)的近鄰查詢算法,這里稱為算法2(略),與算法1過程相同,只是步驟(6)中可信最短路徑期望距離及其可信度的計(jì)算與算法1不同,其正確性證明與時(shí)間復(fù)雜度也與算法1相同。

在現(xiàn)實(shí)應(yīng)用中,還有即時(shí)可信近鄰的查詢需求,這種需求想知道某時(shí)的可信近鄰情況,而不想知道模糊網(wǎng)絡(luò)的整體情況,針對(duì)這種需求,給出算法3。

算法2即時(shí)可信近鄰查詢算法

輸入模糊圖=(V,E,W,Cr),查詢點(diǎn)q∈V,近鄰數(shù)k,距離約束D

輸出k-NN查詢結(jié)果集NNC

算法3的正確性證明與算法1同理。算法3中步驟(3)～步驟(5)是計(jì)算每個(gè)訪問結(jié)點(diǎn)與查詢點(diǎn)的距離及其可信度,其時(shí)間復(fù)雜度為O(e+nlgn),步驟(6)、步驟(7)行是訪問結(jié)點(diǎn)與當(dāng)前近鄰對(duì)象可信度的比較,其時(shí)間復(fù)雜度為O(lg(n)),即算法3的時(shí)間復(fù)雜度為O(e+(n+1)lgn)。

6 實(shí)驗(yàn)結(jié)果分析

實(shí)驗(yàn)在 2.0 GHz雙核處理器、1 GB內(nèi)存、Windows XP平臺(tái)上用Visual C++6.0實(shí)現(xiàn)。實(shí)驗(yàn)數(shù)據(jù)使用2個(gè)路網(wǎng),一個(gè)是人工合成網(wǎng)N1,使用模擬器產(chǎn)生100 000個(gè)平面點(diǎn),隨機(jī)連接點(diǎn)形成邊,對(duì)邊在[1,10]區(qū)間范圍內(nèi)賦權(quán)重,對(duì)邊在[0,1]區(qū)間范圍內(nèi)賦可信度,點(diǎn)的最大出度設(shè)為10。另一個(gè)是實(shí)際路網(wǎng)N2,從Digital Chart of World(DCW)獲得,包含430 274個(gè)結(jié)點(diǎn)、594 104條邊。將邊的可信度設(shè)為邊的通過時(shí)間的倒數(shù)。使用本文所述的存儲(chǔ)結(jié)構(gòu)對(duì)兩個(gè)網(wǎng)絡(luò)進(jìn)行存儲(chǔ),頁(yè)面大小為4K。

實(shí)驗(yàn)分為2個(gè)部分,第1部分測(cè)試可信距離的特征,第2部分測(cè)試各個(gè)參數(shù)對(duì)基于可信距離的近鄰查詢算法的影響。

實(shí)驗(yàn)1測(cè)試可信距離的分布情況。為估計(jì)可信距離分布,在2個(gè)實(shí)驗(yàn)數(shù)據(jù)網(wǎng)中分別抽取300個(gè)樣本,每個(gè)樣本中遍歷300個(gè)結(jié)點(diǎn)累積距離,距離的分布結(jié)果如圖4所示。從圖4可知,2個(gè)實(shí)驗(yàn)網(wǎng)絡(luò)情況相似,2個(gè)距離函數(shù)有相似分布,且與確定圖中最短路徑距離函數(shù)的分布相似。

圖4 可信距離分布

實(shí)驗(yàn)2測(cè)試可信距離的收斂性與樣本數(shù)的關(guān)系。在2個(gè)網(wǎng)絡(luò)中分別以300個(gè)樣本的結(jié)果為基準(zhǔn),計(jì)算不同樣本數(shù)時(shí)近似距離的均方差。結(jié)果如圖5所示,從圖5可知隨著樣本數(shù)的增加,均方差趨于0,可信距離依樣本數(shù)收斂。

圖5 可信距離與樣本數(shù)關(guān)系

實(shí)驗(yàn)3測(cè)試k值與基于可信距離的近鄰查詢算法性能的關(guān)系。因可能成為近鄰查詢結(jié)果的是近鄰查詢過程中Dijkstra算法訪問的結(jié)點(diǎn),故以訪問結(jié)點(diǎn)數(shù)與圖的總結(jié)點(diǎn)數(shù)的比值為主要衡量標(biāo)準(zhǔn),來評(píng)估近鄰算法的的性能。圖6是樣本數(shù)為200時(shí),訪問結(jié)點(diǎn)數(shù)與k值的關(guān)系結(jié)果圖,從圖6可知隨著k值增加,訪問結(jié)點(diǎn)數(shù)緩慢增加,近鄰查詢算法的性能隨之下降。

圖6 k值與算法性能關(guān)系

實(shí)驗(yàn)4測(cè)試樣本數(shù)與基于可信距離的近鄰查詢算法性能的關(guān)系。圖7是k=20時(shí),訪問結(jié)點(diǎn)數(shù)與樣本數(shù)的關(guān)系結(jié)果,從圖7可知隨著樣本數(shù)增加,訪問結(jié)點(diǎn)數(shù)初期也急劇增加,但樣本數(shù)達(dá)到一定數(shù)值后,訪問結(jié)點(diǎn)數(shù)漸趨平穩(wěn),沒有出現(xiàn)性能極劇惡化的情況。

圖7 樣本數(shù)與基于可信距離的近鄰查詢算法性能關(guān)系

距離約束D和精度ε分別影響訪問結(jié)點(diǎn)數(shù)和樣本數(shù),從而間接影響算法性能。隨著距離約束D的增大和精度ε的提高,算法性能下降。

7 結(jié)束語(yǔ)

針對(duì)不確定網(wǎng)絡(luò)空間近鄰查詢問題,將不確定網(wǎng)絡(luò)建模為模糊圖,給出模糊圖中可信最短路徑距離與可信最短路徑期望距離定義,以可信距離為度量,提出可信近鄰查詢概念,并給出距離受限條件下的可信近鄰查詢算法和即時(shí)可信近鄰查詢算法。算法使用取樣方法進(jìn)行近似計(jì)算,使時(shí)間復(fù)雜度為指數(shù)級(jí)的問題在多項(xiàng)式時(shí)間內(nèi)解決,并可根據(jù)實(shí)際需要進(jìn)行精度調(diào)節(jié)。理論分析與實(shí)驗(yàn)結(jié)果表明算法可行且性能穩(wěn)定。下一步的研究是同時(shí)考慮不確定網(wǎng)絡(luò)的隨機(jī)性與模糊性,提高不確定網(wǎng)絡(luò)的描述能力,使不確定網(wǎng)絡(luò)環(huán)境下的近鄰查詢更有效。

[1] Cheng R,Kalashniko V D V,Prabhakar S.Querying Imprecise Data in Moving Object Environments[J]. IEEE Transactions on Knowledge and Data Engineering, 2004,16(9):1112-1127.

[2] 莊 毅.ISU-Tree:一種支持概率k近鄰查詢的不確定高維索引[J].計(jì)算機(jī)學(xué)報(bào),2010,33(10):1934-1941.

[3] Yi Ke,Li Feiei,Kollios G,et al.Efficient Processing of Top-k Queries in Uncertain Databases with X-relations[J]. IEEE Transactions on Knowledge and Data Engineering, 2008,20(12):1669-1682.

[4] 高 峻,郝忠孝.受限網(wǎng)絡(luò)移動(dòng)對(duì)象的概率最近鄰查詢[J].計(jì)算機(jī)工程,2013,39(7):26-30.

[5] 陳逸菲,秦小麟.NU2RA:一種路網(wǎng)中不確定移動(dòng)對(duì)象范圍查詢分析方法[J].計(jì)算機(jī)研究與發(fā)展,2010, 47(6):1060-106.

[6] Adar E,Re C.Managing Uncertainty in Social Networks[J]. IEEE Data Engineering Bulletin,2007,30(2):15-22.

[7] Ghosh J,Ngo H,Yoon S,et al.On a Routing Problem Within ProbabilisticGraphsand ItsApplication to Intermittently Connected Networks[C]//Proceedings of INFOCOM’07.[S.1.]:IEEE Press,2007:216-222.

[8] Asthana S,King O D,Gibbons F D,et al.Predicting Protein Complex Membership Using Probabilistic Network Reliability[J].Genome Research,2004,14(1): 1170-1175.

[9] Potamias M,Bonchi F,Gionis A,et al.Nearest-neighbor Queries in Probabilistic Graphs[EB/OL].[2009-10-21]. http://www.cs.bu.edu.

[10] Schneider M. Fuzzy Topological Predicates, their Properties,and their Integration into Query Languages[C]//Proceedins of the 9th ACM International Symposium on Advances in Geographic Information Systems.New York,USA:[s.n.],2001:212-221.

[11] Tang X,Kainz W.Analysis of Topological Relations between Fuzzy Regions in a General Fuzzy Topological Space[C]//Proceedings of Canadian Geomatics Conference.Ottawa,Canada:[s.n.],2002:114-129.

[12] Zheng Kai,Fung Pui Cheong,Zhou Xiaofang.K-Nearest Neighbor Search for Fuzzy Objects[C]//Proceedings of 2010 ACM SIGMOD International Conference on Management of Data.Indiana,USA:IEEE Press,2010: 333-345.

[13] Zadeh L A.Fuzzy Sets as a Basis for a Theory of Possibility[J].Fuzzy Sets and Systems,1978,(1): 3-28.

[14] Zadeh L A.Mathematical Frontiers of the Social and Policy Sciences[M].Boulder,USA:Westview Press,1979.

[15] Liu Baoding,Liu Yankui.Expected Value of Fuzzy Variable and Fuzzy Expected Value Models[J].IEEE Transactions on Fuzzy Systems,2002,10(4):445-450.

[16] Liu B.Uncertainty Theory:An Introduction to Its Axiomatic Foundations[M].Berlin,Germany:Springer-Verlag,2004.

編輯 索書志

Credible Nearest Neighbor Query in Constraint Fuzzy Network

GAO Jun1,HAO Zhongxiao1,2
(1.College of Computer Science and Technology,Harbin University of Science and Technology,Harbin 150080,China; 2.College of Computer Science and Technology,Harbin Institute of Technology,Harbin 150001,China)

This paper gives a new method for solving the problem of the nearest neighbor query in uncertain network.The method is that,gives the definition of credible shortest path distance and credible shortest path expectation distance,based on credible distance,puts forward the concept of fuzzy graph credible nearest neighbor query,and proposes fuzzy graph credible nearest neighbor query algorithm and instant credible nearest neighbor query algorithm on the condition of network distance constraint.The algorithm decreases the difficulty of the problem by using fuzzy analog,diminishes search space by using network distance constraint and quickly acquires the result of credible nearest neighbor query according to the precisionε by using the priority queue.The complexity of the algorithm isO((2r+Δr)(e+nlgn)+hlgh+lgn)andO(e+(n+1)lgn). Theory analysis and experimental results show that fuzzy graph credible nearest neighbor query algorithm can solve the problem of the nearest neighbor query in uncertain network at the angle of fuzzy quality.

uncertain network;fuzzy graph;credible distance;credible nearest neighbor;fuzzy analog;distance constraint

1000-3428(2015)01-0054-07

A

TP311.13

10.3969/j.issn.1000-3428.2015.01.010

黑龍江省自然科學(xué)基金資助項(xiàng)目(F200821)。

高 峻(1972-),女,副教授、博士研究生,主研方向:時(shí)空數(shù)據(jù)庫(kù)技術(shù);郝忠孝,教授、博士生導(dǎo)師。

2013-09-24

2013-12-26 E-mail:hustgj@163.com

中文引用格式:高 峻,郝忠孝.受限模糊網(wǎng)絡(luò)可信近鄰查詢[J].計(jì)算機(jī)工程,2015,41(1):54-60.

英文引用格式:Gao Jun,Hao Zhongxiao.Credible Nearest Neighbor Query in Constraint Fuzzy Network[J].Computer Engineering,2015,41(1):54-60.