基于用戶特征遷移的協同過濾推薦

柯良文,王 靖

(華僑大學計算機科學與技術學院,福建廈門361021)

·先進計算與數據處理·

基于用戶特征遷移的協同過濾推薦

柯良文,王 靖

(華僑大學計算機科學與技術學院,福建廈門361021)

為提高推薦系統在數據稀疏情況下的推薦質量,提出一種基于用戶特征遷移的協同過濾推薦模型。利用矩陣分解技術提取輔助領域的用戶特征,通過建立正則項約束的矩陣分解模型,將輔助領域的用戶特征遷移到目標領域中,協助目標領域用戶特征的學習,最終生成目標領域的用戶推薦。設計快速收斂的Wiberg算法得到模型的最優解,并對實際應用中的可行性進行分析。通過對2個公開數據集的實驗結果表明,該模型能夠實現輔助領域用戶特征的遷移,有效提高目標領域的推薦質量。

數據稀疏;用戶特征遷移;協同過濾;矩陣分解;Wiberg算法

1 概述

隨著互聯網的不斷普及和應用,網絡上的信息量正呈指數式的增長。用戶一方面可以方便獲取到豐富信息,另一方面則要面臨過量信息伴隨著的信息過載問題[1]:無法從海量的信息中獲取到對自己有用的部分。個性化推薦系統根據用戶的喜愛和偏好,從海量的信息中發現用戶感興趣和有價值的信息,并將其推薦給用戶。目前,推薦系統已應用到多種領域,如電子商務網站的 Amazon,eBay等,電影網站的MovieLens,Reel.com等,新聞網站的GroupLens等。

協同過濾是推薦系統應用最為成功的技術之一,其基本假設是:如果用戶X和用戶Y對于n個項目有相似的評分或購買行為,那么他們對其他項目也會有類似的評價。根據這一假設,協同過濾技術首先要度量目標用戶和其他用戶的相似度,然后選取與目標用戶相似度最高的前k個用戶作為最近鄰居,最后通過這些最近鄰居的興趣偏好為目標用戶作出推薦。然而在實際的應用中,用戶評分的項目在整個項目集中往往只占其中一小部分,導致整個評分矩陣十分稀疏,從而在計算用戶間的相似度時不夠準確,降低了推薦系統的推薦質量。

針對協同過濾出現的稀疏性問題,研究者提出了多種不同解決辦法,如文獻[2]利用奇異值分解(Singular Value Decomposition,SVD)技術移除沒有代表性或者無關緊要的用戶和項目,以達到用戶-項目評分矩陣降維的目的;文獻[3]提出了一種先聚類再經過非負矩陣分解的兩階段聯合聚類協同過濾算法,通過縮小原始評分矩陣規模以提高非負矩陣分解算法面對稀疏矩陣預測上的準確度;文獻[4]提出了一種變權重相似度計算和自適應局部融合參數的協同過濾算法,來緩解數據稀疏和數據集異構的問題;文獻[5]提出一種基于奇異值分解和增強Pearson相關系數的特征遞增算法(HybridSVD)來克服數據稀疏性的問題。然而,這些方法普遍存在一個問題:只局限在單個領域的學習任務中,而沒有利用其他領域的知識來改善推薦系統的質量。近年來,多領域學習成為推薦系統的一個新的研究方向[6-7],特別是將遷移學習的方法應用到協同過濾算法中已受到學者們的關注。關于遷移學習在協同過濾技術應用的研究現狀,本文將做詳細介紹。

針對數據稀疏的問題,本文在矩陣分解模型的基礎上,基于遷移學習的思想,提出一種用戶特征遷移的協同過濾推薦模型(TUF)。通過學習輔助領域的用戶特征,并將其遷移到目標領域的學習任務中,幫助提高目標領域的推薦精度。同時,采用Wiberg算法對目標模型進行快速求解以獲得最優解。

2 相關研究

2.1 問題定義

推薦系統中普遍采用一個m×n的矩陣R表示所有用戶對項目的評分,R的行列數m和n分別表示用戶數和項目數。R的元素值ri,j∈{「a,b」U}代表用戶對項目的評分,其中,a和b分別代表評分值的上下限;?表示該項未評分。通過一個與評分矩陣R大小相同的標記矩陣W來表示某一項是否被評分,W的元素值wi,j∈{0,1},其中0代表該項未評分,1代表該項已評分。協同過濾的目標就是通過評分矩陣R已知的評分項去預測未知項的評分值。

2.2 基于矩陣分解的協同過濾

基于矩陣分解的協同過濾技術認為用戶-項目評分矩陣R是一個近似逼近低秩的矩陣[8],采用矩陣Z表示無缺失值的評分矩陣,并且用d表示Z的秩,其中,d＜＜min(m,n),那么Z可以分解成如下形式:

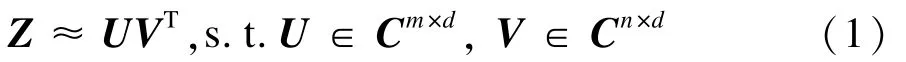
分解后的矩陣U和矩陣V可以分別表示用戶特征矩陣和項目特征矩陣。實際情況下,用戶-項目評分矩陣R是帶有噪聲的矩陣,假設噪聲符合等方向的高斯分布,則對于U和V的最優估計可以通過下面的的損失函數來確定:

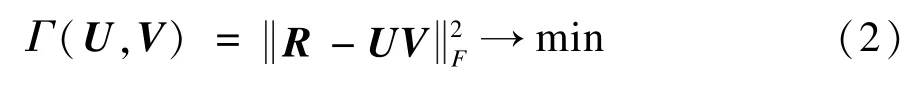
其中,||·||F表示Frobenius范數。

在實際應用中,由于R是一個極度稀疏的矩陣(缺失項用零填充),因此需要對這些零元進行單獨處理。通過引入加權的矩陣分解方法可以在計算損失函數時剔除掉這些零元,而只考慮非零項。修改后的矩陣分解模型可以表示成以下形式:

其中,Γ表示 Hadamard積(Hadamard積定義為: (W☉R)i,j=Wi,jRi,j)。為避免過度擬合,在模型式(3)加入正則項,則進一步修改后的矩陣分解模型如下所示:

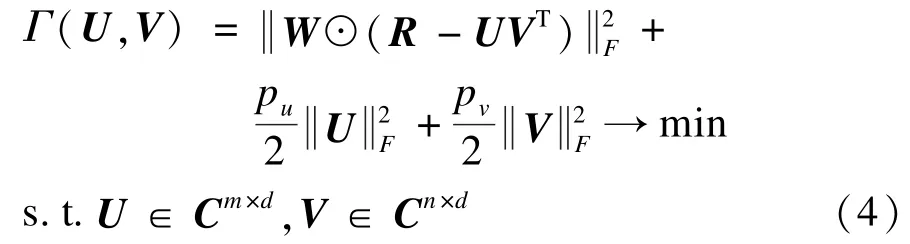
對于模型式(4),pu和pv為正則項的控制參數,用來協調實際用戶評分矩陣和矩陣分解模型學習后的填充矩陣之間的訓練集誤差。

2.3 應用遷移學習的協同過濾推薦算法

遷移學習(又稱多任務學習)是一種新的機器學習框架,它不同于傳統的監督學習、非監督學習和半監督學習。為了描述這種方法,本文引用文獻[9]給出的關于遷移學習的一般性定義:給定一個輔助領域DS及它的學習任務TS和一個目標領域DT及其學習任務TT,遷移學習的目標是利用DS和TS的知識來幫助提高DT的目標預測函數fT(·),其中DS≠DT,或者TS≠TT。

根據不同的遷移知識,遷移學習方法可以分成3種:基于模型的遷移,基于特征的遷移,基于樣本的遷移。目前,研究者針對不同的遷移學習方法提出了各種相應的協同過濾推薦算法,其中基于模型的遷移方法有:評分矩陣生成模型(Rating Matrix Generative Model,RMG-M)[10]等;基于特征的遷移方法有聯合矩陣分解(Collective Matrix Factorization,CMF)[11]、坐標系統遷移(Coordinate System Transfer,CST)[12]等;基于樣本的遷移方法有:集成分解遷移(Transfer by Integrative Factorization,TIF)[13]。從本質上看,本文提出的TUF模型屬于基于特征的遷移方法。

3 基于用戶特征遷移的協同過濾推薦模型

在現實世界中,不同的電子商務網站擁有共同的用戶群,而這些用戶在不同的電子商務網站上對商品的評價有相似的評價模式,例如用戶X在某電影網站對科幻類的電影有較高的評價,則該用戶在某書籍網站上對與科幻相關的書籍應該也有較高的評價。通過挖掘較成熟領域(輔助領域)用戶的潛在評價模式可以用來幫助新領域(目標領域)的相關學習任務。為此,本文提出了一種基于用戶特征遷移的協同過濾推薦模型,基本流程如圖1所示。

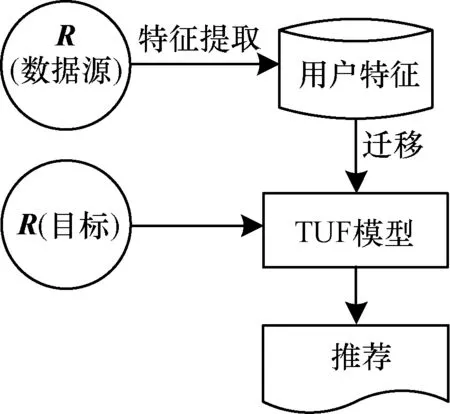
圖1 TUF模型的基本流程

為了將遷移學習應用到協同過濾算法中,首先需要考慮遷移什么樣的知識,即如何從輔助領域中學習用戶特征UL。本文將采用核范數正則化用于從輔助領域的評分矩陣中學習用戶的特征。記RA為輔助領域的用戶-項目評分矩陣,WA為輔助領域的標記矩陣,則核范數正則化最小二乘模型的構造如下:

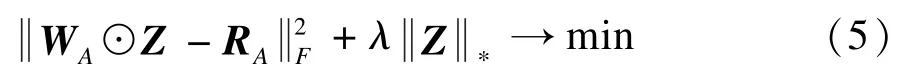
其中,||Z||?表示Z的核范數,即矩陣Z的所有奇異值之和。文獻[14]給出了模型(5)的求解算法SOFT-IMPUTE。令Z=USVT為矩陣Z的奇異值分解,Sd為Z的前d個最大奇異值構造的奇異值矩陣,Ud為前d個最大奇異值對應的左奇異向量。顯然,表示了從輔助領域的評分矩陣中提取的d個用戶特征。本文采用模型(5)提取輔助領域的用戶特征基于下面3個原因:

(1)模型(5)通過多次的SVD分解進行迭代求解,能更準確地提取稀疏矩陣的特征信息;

(2)由于每一層迭代的SVD分解只需要計算前k個最大的奇異值(k＜＜m,n),模型(5)的求解算法可以應用于大規模數據處理。這將有利于有較豐富數據的輔助領域(例如,項目數比較多)的任務學習;

(3)模型(5)不涉及到矩陣的維度,可以減少用戶的參數設置。

下一步將決定如何遷移知識,即如何將從輔助領域中學習到的用戶特征UL,用于幫助學習目標領域的用戶特征U,進一步的再用于幫助目標領域的用戶-項目評分預測。從理論上看,當輔助領域和目標領域的用戶、項目完全一致時,2個領域的用戶特征應具有一致性,即UL=U。然而在實際應用中,由于輔助領域和目標領域的差異,2個領域的用戶特征雖然相似,卻并不會完全相同。因此,本文通過引入正則項來確保UL和U的相似性。將正則項引入模型(3),并引入正則項來避免過擬合,本文構造基于用戶特征遷移的協同過濾推薦模型如下:

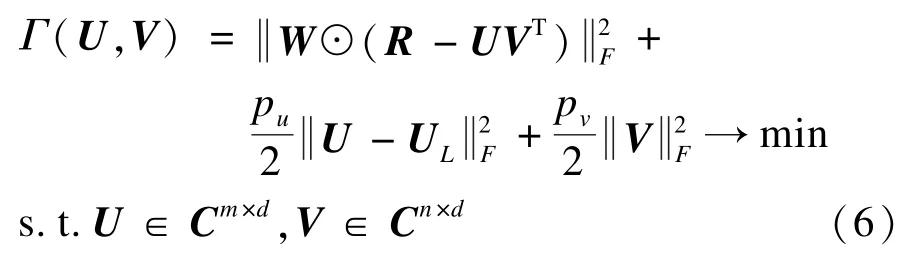
其中,pu和pv是控制參數。pu越大時,表示目標領域的用戶特征矩陣U越接近于輔助領域的用戶特征矩陣UL。顯然,當pu趨近于無窮大時,U將完全等同于UL;當pu趨近于0時,模型對于目標領域的學習任務將沒有利用輔助領域的知識。

與文獻[12]提出的CST模型相比較,本文的TUF模型沒有對用戶特征矩陣和項目特征進行正交性約束,其主要原因有:(1)用戶特征或項目特征不一定表現出正交性;(2)從數學角度看,2個正交矩陣之間的距離表現為其張成的子空間距離,因而用F范數來度量2個正交矩陣的距離并不合理。由于沒有正交性的約束,CST模型的求解方法將不適用于TUF模型,因此在本文第4節中將給出TUF模型的具體求解算法。

4 基于Wiberg算法的TUF模型求解

本文提出的TUF模型核心在于求解目標領域的用戶特征矩陣U和項目特征矩陣V,使模型達到或逼近最優解。文獻[15]提出一種數值算法來解決帶缺失值的矩陣分解模型。此后,研究者提出了多種迭代算法來解決這類最優化問題,例如文獻[8]提出一種Damped-Newton算法來求解式(4)的矩陣分解模型。在這些算法中,Wiberg算法[16]由于對初始值不敏感,并能以快速的迭代速度在全局范圍內到達收斂,具有較好的數值表現效果。近年來,文獻[17]進一步對Wiberg算法進行研究。然而,由于文獻[17]提出的算法主要在于解決沒有帶正則項的式(3)缺失矩陣分解模型,并不適合本文提出的TUF模型。因此,本文將重新討論TUF模型求解方法的具體方案。根據文獻[17]利用Wiberg算法求解缺失矩陣分解模型的基本思想,本文首先對TUF模型進行適當的變型。

令u,ul∈Cmd,v,ul∈Cnd分別是由矩陣U,Ul∈Cm×d,Vl∈Cn×d的各行向量進行向量化得到的新向量,如,v=vec(V)=記s為目標領域用戶-項目評分矩陣R所有已評分項的數目,r=[ri,j]∈Cs是一個只包含已評分項的向量,其中,ri,j表示R的第i行第j列元素。為了消去模型(5)中標記矩陣W,構造一個由v1,v2,…,vn構成的s×md的矩陣P和一個由u1,u2,…,um構成的s×nd的矩陣Q,即:

則模型(6)可以重新構造為:

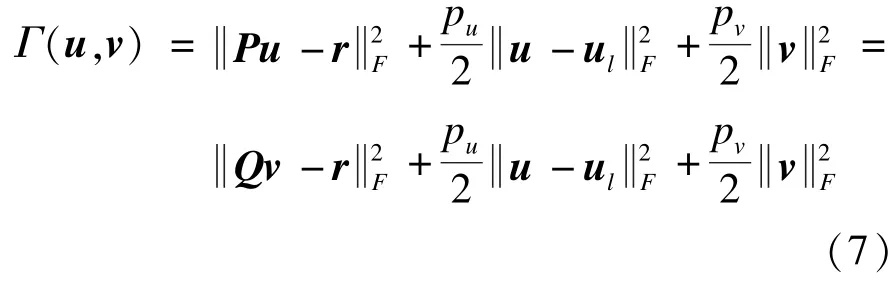
注意到上面的形式只是為了描述方便而表示的矩陣基本結構,由于要處理缺失的項,矩陣P和Q將只保留與已知項相對應的行,例如,如果ri,j是缺失值,則要移除P和Q的((i-1)×n+j)行。因此,P和Q的行向量數等于已知評分項的總個數s。

4.1 Wiberg算法的公式推導

為了求解模型(7)的最優解,傳統的 Gauss-Newton方法定義向量x=[uT,vT]T,并通過尋找dΓ/dx=0迭代更新解向量x。在每次迭代中, Gauss-Newton方法對變量u,v進行同時更新。與傳統的Gauss-Newton方法不同,Wiberg算法分別對變量u,v進行更新[16]。對給定v,可以通過計算 ?Γ/?u=(PTP+puI)u-(PTr+puul)=0對u進行更新,即有:

在對v進行更新時,Wiberg算法將參數u看作是v的函數,即u=(v),則TUF模型中的最優化問題便可以轉化成只有一個參數變量v的損失函數φ(v):

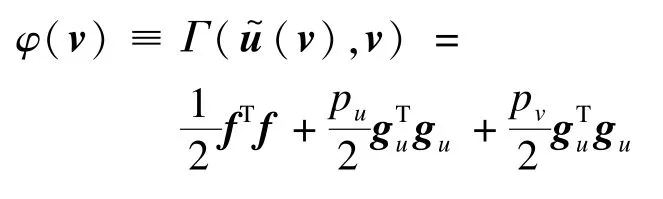
其中,f≡f(v)≡g((v),v)=(v)-r;gu≡gu(v)=(v)-ul;gv≡gv(v)=v。記v+φv為更新后的v變量,對φ(v)二階泰勒展開,可得:

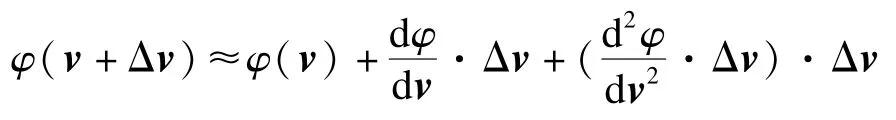
構造φv極小化上式中的泰勒展開式,即可獲得v的更新量

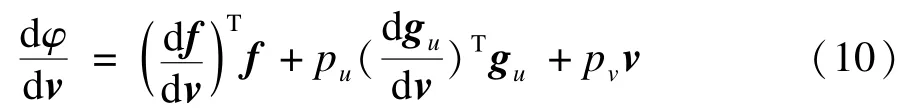
以及:

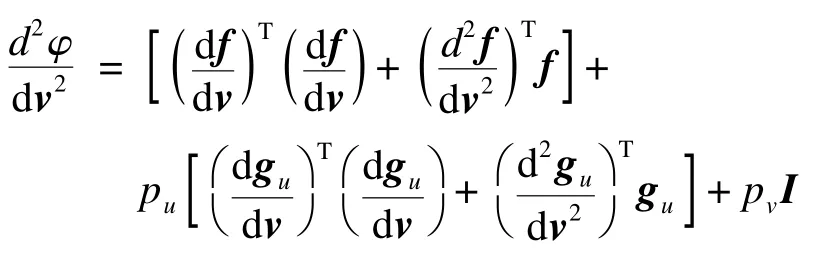
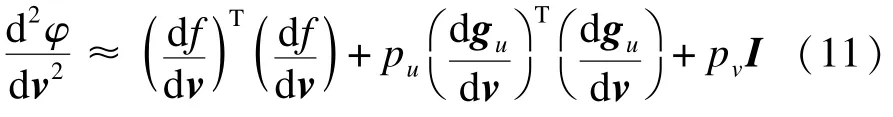
進一步,分別對f(v)和gu(v)進行求導。因為,由復合函數求導法則:

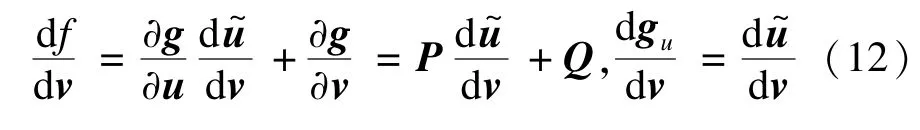
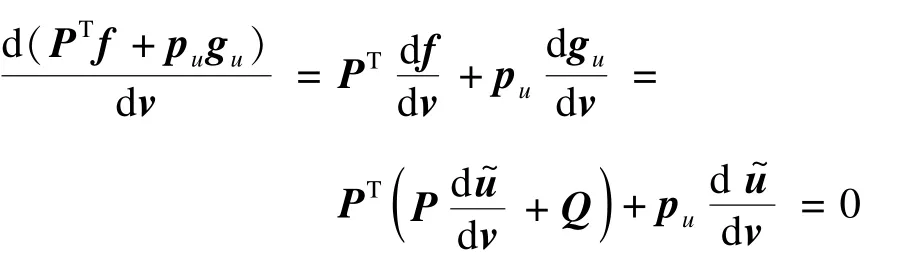
整理上式,即有:

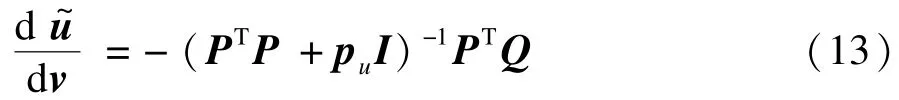
將式(13)代入式(12),可以得到:

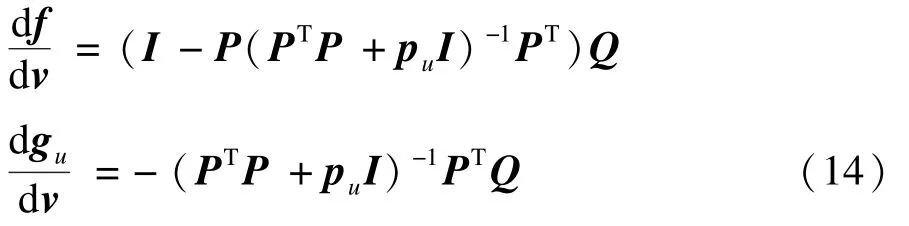
將式(14)分別代入式(10)和式(11),即可獲得Hessian矩陣以及

4.2 算法描述

根據上節的相關公式推導,對于TUF模型的求解方法,有具體如下的Wiberg算法:

算法Wiberg算法

輸入輔助領域的評分矩陣RA和目標領域的評分矩陣R,正則項參數pu和pv。

輸出目標領域的預測評分矩陣Z。

Step1通過SOFT-IMPUTE算法對輔助領域的最優化模(5)進行填充,得到RA的近似低秩逼近矩陣ZA。

Step2對ZA進行奇異值分解,即有ZA=USVT,得到輔助領域的用戶特征

Step3隨機初始化v,并通過UL和R構造出ul和r。

Step4由v構造P矩陣,并根據式(8)對u進行更新。

Step5如果收斂則跳轉至 Step8,否則轉至Step6。

Step6由u構造Q矩陣,計算和,并根據式(9)式求解Δv,更新v←v+Δv。

Step7如果收斂則跳轉至Step8,否則跳轉至Step4。

Step8通過u和v構造出矩陣U和V,并計算Z=UVT。

在Wiberg算法中,計算量主要集中在式(8)和式(9)。在實際應用中,為了減小時間和空間的復雜度,算法并不需要直接生成矩陣的逆,而是通過求解線性方程組以獲取u和v更新向量。例如,式(8)、式(9)等價于求解線性方程組:

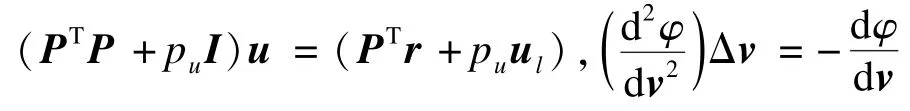
5 實驗與結果分析

5.1 實驗數據集

為了驗證本文模型的有效性,采用互聯網上2個公開的數據集對算法進行測試和驗證。

(1)MovieLens數據集

數據來源:http://www.grouplens.org/node/ 73。該數據集中的評分數據包含943個獨立用戶對1682部電影(共包含19類電影)進行10萬次評分的數據(評分1～5)。隨機選擇500個用戶對所有電影的評分數據,要求每個用戶至少評價過30部以上的電影。在該數據集上進行5組實驗,每組實驗選取一種電影類別的評分數據作為目標領域的數據集,而其余電影類別的評分數據則作為輔助領域的數據集。對目標領域的數據集,按照4∶1的比例將其進一步劃分為訓練集和測試集。數據集的具體描述見表1。這里稀疏度定義為已評分數據占整個領域數據集的比例。

表1 MovieLens評分數據集描述

(2)EachMovie數據集

數據來源:http://research.compaq.com/SRC/ eachmovie。該數據集約有7.2萬個用戶對1 628部電影進行2.8百萬次評分的數據(評分1～6),為了評分數據的統一,實驗時將原來的評分6由評分5來代替。在該數據集上隨機抽取500個用戶,并對電影項目進行隨機劃分:1 000部電影作為輔助領域的項目,500部電影作為目標領域的項目,每個用戶在輔助領域和目標領域里都至少評價過25部以上的電影。進一步地,劃分目標領域的訓練集和測試集,其中訓練集根據目標領域的用戶評價數劃分為4組,每組用戶的評價數依次為10,15,20,25,對應的其余評分數據作為測試集。

5.2 評價指標

本文采用平均絕對誤差(Mean Absolute Error, MAE)作為評價評分預測準確性的標準。平均絕對誤差通過計算預測的用戶評分和實際的用戶評分之間的偏差來度量預測的準確性,具體計算方法如下:

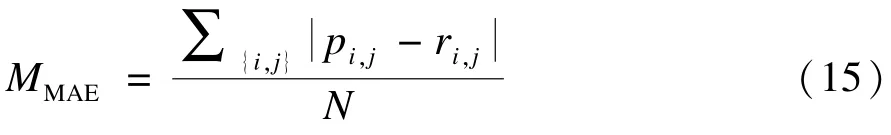
其中,N為測試集的用戶評分數;pi,j表示用戶i對項目j的預測評分值;ri,j表示實際評分值。MAE越小,推薦質量越高。每組實驗均進行5次隨機實驗(即對訓練集進行隨機劃分),并取平均值作為最終的評價結果。

5.3 對比算法和參數設置

為了驗證TUF模型能否有效提高推薦系統的推薦質量,選擇3種非遷移學習算法:PCC、Soft-Impute(SD)和TMF,2種遷移學習算法:CMF和Soft-Impute(MD)作為比較方法。其中,PCC是基于Pearson相關相似性(Pearson Corelation Coefficients, PCC)的最近鄰協同過濾算法[19];Soft-Impute(SD)是單個領域的 Soft-Impute算法(Soft-Impute on Single Domain),即只對目標領域評分矩陣進行預測填充缺失項;TMF是傳統的矩陣分解方法(Traditional Matrix Factorization)[8],即上文的模型(4);CMF為文獻[11]提出的基于多領域數據的聯合矩陣分解模型;Soft-Impute(MD)為多個領域的Soft-Impute算法(Soft-Impute on Multiple Domains),即對目標領域和輔助領域構成的評分矩陣進行預測填充缺失項。而其他的一些遷移學習算法,如CST模型[12]同時應用到了用戶特征和項目特征,TCF模型[20]對輔助領域和目標領域要求有共同的用戶集和項目集。本文實驗的數據集并不符合這些要求,因此對于這些算法本文不進行實驗比較。

在參數設置上,對有利用到用戶特征數的模型(TMF,CMF和TUF)本文嘗試選擇不同的用戶特征數:d∈{3,4,…,10}。在PCC算法中,選擇的最近鄰居數為{5～120}。對于TMF模型,正則項的參數設置如下:pu=pv={0.1,0.5,1,5,10}。對于CMF模型,選擇’Identity’作為目標領域和輔助領域的預測函數(prediction link),其他參數的設置如下:α=0.5,pu=pz={0.1,0.5,1,5,10},pv={0.1,0.5,1, 5,10,20}。在2種不同領域的Soft-Impute算法中,對參數λ的設置范圍為{1,2,…,20}。對于本文的TUF模型,正則項的參數設置如下:pu={1,5,10, 50},pv={1,2,5,10},并且pu≥pv。

5.4 實驗結果

每個算法的實驗結果為在上一小節的參數設定范圍內取得的最優效果。表 2和表 3分別為MovieLens和EachMovie目標領域測試集上的實驗結果。

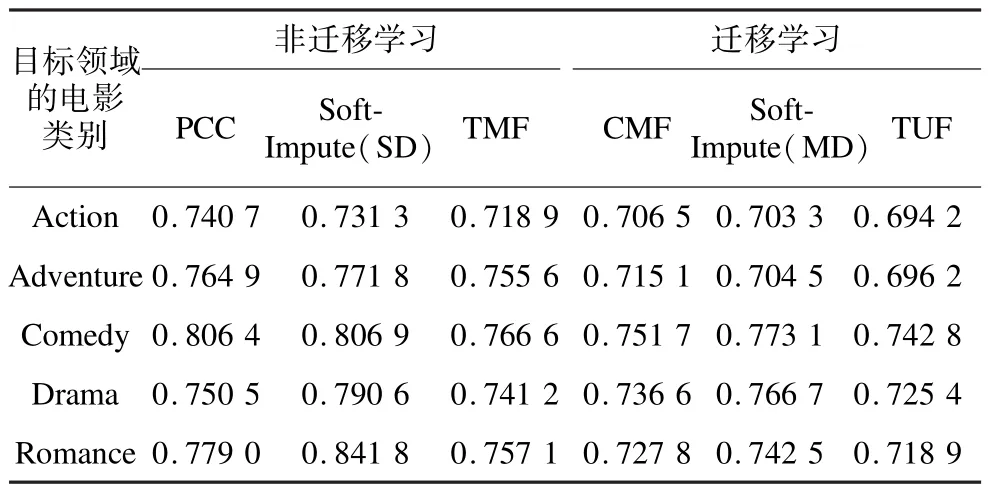
表2 6種算法在不同電影類別下的MAE指標比較

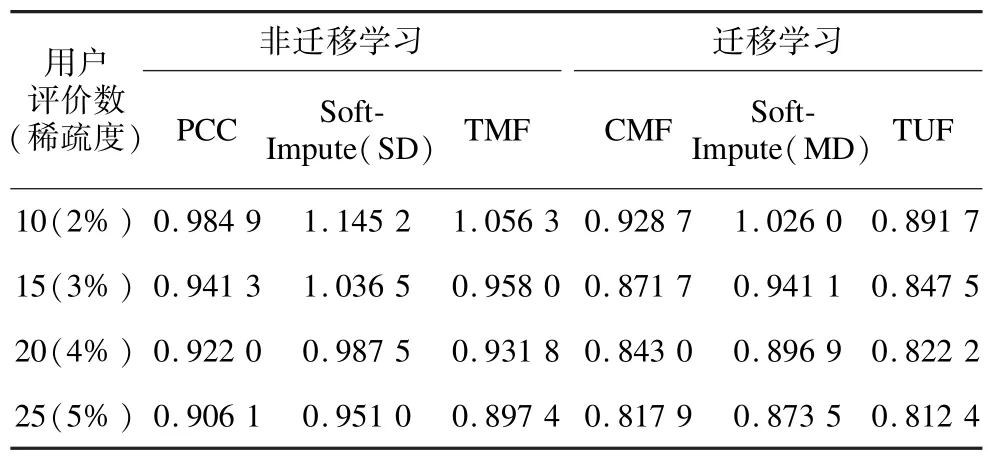
表3 6種算法在不同數據稀疏度下的MAE指標比較

從表2和表3可以看出,幾乎所有遷移學習方法的結果均好于非遷移學習方法的結果。這種對比在Soft-Impute(SD)和Soft-Impute(MD),TMF和TUF上體現的尤為明顯。值得一提的是,Soft-Impute(SD)和TMF可以認為是Soft-Impute(MD)和TUF在無遷移學習下的特例。這表明了遷移學習方法利用了輔助領域的信息,能有效提高目標領域的推薦質量。而在所有的遷移學習方法中,TUF模型均取得了最好的推薦結果。這表明了和CMF, Soft-Impute(MD)方法相比,TUF能更為有效的利用輔助領域的用戶特征信息。

此外,表3的結果還表明,稀疏度越低,TUF取得的優勢越明顯。例如在表3的結果中,與CMF模型相比較,稀疏度為5%的測試結果MAE值減少了0.005,而稀疏度為2%的測試結果MAE值減少了0.037。這說明對評分數據極其稀疏的情形,TUF模型體現了更好的適應性,能有效緩解數據稀疏的問題。

6 結束語

本文在矩陣分解和遷移學習方法的基礎上,提出了一種用戶特征遷移的協同過濾推薦模型(TUF),以緩解數據稀疏的問題。為提取輔助領域的用戶特征信息,本文并沒有簡單地利用SVD方法進行獲取,而是先通過Soft-Impute算法對輔助領域的缺失評分矩陣進行填充,然后對其奇異值分解獲取更為準確的用戶特征。通過TUF模型對輔助領域的用戶特征進行遷移,幫助目標領域的用戶對未評分項目的預測。此外,本文采用能夠快速達到收斂的Wiberg算法對模型進行迭代求解以獲得最優解。實驗結果表明,引入特征遷移的矩陣分解模型相比較于傳統的矩陣分解模型和其他遷移學習算法,能有效緩解評分矩陣數據極端稀疏情況,顯著提高推薦系統的推薦質量。

本文模型雖然只利用輔助領域的用戶特征信息,但也適用于輔助領域和目標領域有共同項目集時對項目特征的遷移,而如何改進模型使其能夠同時對用戶特征和項目特征進行遷移是下一步的研究方向。

[1] 許海玲,吳 瀟,李曉東,等.互聯網推薦系統比較研究[J].軟件學報,2009,20(2):350-362.

[2] Billsus D,Pazzani M J. Learning Collaborative Information Filters[C]//Proceedings of ICML’98. Madison,USA:[s.n.],1998:54-48.

[3] 吳 湖,王永吉,王 哲,等.兩階段聯合聚類協同過濾算法[J].軟件學報,2010,21(5):1042-1054.

[4] 程小林,熊 焰,劉青文,等.一種基于自適應局部融合參數的協同過濾方法[J].計算機工程,2014, 40(1):39-44.

[5] 曾小波,魏祖寬,金在弘.協同過濾系統的矩陣稀疏性問題的研究[J].計算機應用,2010,30(4):1079-1082.

[6] Li Bin.Cross-domain Collaborative Filtering:A Brief Survey[C]//Proceedings of the 23rd International Conference on Tools with Artificial Intelligence. [S.l.]:IEEE Press,2011:1085-1086.

[7] Ning X,Karypis G.Multi-task Learning for Recommender System[C]//Proceedings of the 2nd Asian Conference on Machine Learning.Tokyo,Japan:[s.n.],2010:269-284.

[8] Buchanan A M,Fitzgibbon A W.Damped Newton Algorithms for Matrix Factorization with Missing Data[C]// Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE Press,2005:316-322.

[9] Sinno J P,Yang Qiang.A Survey on Transfer Learning[J].IEEE Transactions on Knowledge and Data Engineering,2010,22(10):1345-1359.

[10] Li Bin,Yang Qiang,Xue Xiangyang.Transfer Learning for Collaborative Filtering via a Rating-matrix Generative Model[C]//Proceedings of the 26th Annual International Conference on Machine Learning.Quebec, Canada:[s.n.],2009:617-624.

[11] Singh A P,Gordon G J.RelationalLearning Via Collective Matrix Factorization[C]//Proceedings of the 14th ACM SIGKDD InternationalConference on Knowledge Discovery and Data Mining.[S.l.]:ACM Press,2008:650-658.

[12] Pan Weike,Evan W X,Lin N,et al.Transfer Learning in Collaborative Filtering for Sparsity Reduction[C]// Proceedings of the 24th AAAI Conference on Artificial Intelligence.[S.l.]:AAAI Press,2010:230-235.

[13] Pan Weike,Evan W X,Yang Qiang.Transfer Learning in Collaborative Filtering with Uncertain Ratings[C]// Proceedings of the 26th AAAI Conference on Artificial Intelligence.Toronto,Canada:AAAIPress,2012: 662-668.

[14] Mazumder R,Hastie T,Tibshirani R.Spectral Regularization Algorithms for Learning Large Incomplete Matrices[J]. Journal of Machine Learning Research,2010,(11):2287-2322.

[15] Golub G H,van Loan C F.Matrix Computations[M]. Baltimore,USA:Johns Hopkins University Press,1996.

[16] Wiberg T.Computation of Principal Components When Data are Missing[C]//Proceedings of the 2nd Symposium on Computational Statistics.Berlin,Germany: [s.n.],1976:229-236.

[17] Okatani T,Deguchi K.On the Wiberg Algorithm for Matrix Factorization in the Presence of Missing Components[J].International Journal of Computer Vision, 2007,72(3):329-337.

[18] 李 改,李 磊.基于矩陣分解的協同過濾算法[J].計算機工程與應用,2011,47(30):4-7.

[19] Resnick P,Iacovou N,Suchak M,et al.GroupLens:An Open Architecture for Collaborative Filtering of Netnews[C]//Proceedings of ACM Conference on Computer Supported Cooperative Work.North Carolina,USA: ACM Press,1994:175-186.

[20] Pan W,Liu N N,Xiang E W,et al.Transfer Learning to Predict Missing Ratings via Heterogeneous User Feedbacks[C]//Proceedings of the 22th International Joint Conference on Artificial Intelligence.[S.l.]:AAAI Press,2011:2318-2323.

編輯 金胡考

Collaborative Filtering Recommendation Based on User Feature Transfer

KE Liangwen,WANG Jing
(School of Computer Science and Technology,Huaqiao University,Xiamen 361021,China)

In order to improve the recommendation quality of recommender system with data sparsity,this paper proposes a user collaborative filtering recommendation model based on feature transfer.Firstly,matrix factorization technology is applied to collect the user feature from the auxiliary domain.Secondly,it constructs a matrix factorization model with the constraint of regularization term,which is used to transfer the user feature learned from the auxiliary domain to the target domain,so as to help the learning of user feature in the target domain.Finally,user recommendation is made for the target domain.A fast convergence Wiberg algorithm is also designed for the model to get the optimal solution,whose feasibility is also discussed for practical application.Through the experiment on two real world data sets, the model can effectively transfer the user feature of source domain,and improve the quality of recommender system for target domain.

data sparsity;user feature transfer;collaborative filtering;matrix factorization;Wiberg algorithm

1000-3428(2015)01-0037-07

A

TP311

10.3969/j.issn.1000-3428.2015.01.007

國家自然科學基金資助項目(61370006);福建省高等學校杰出青年科研人才培育計劃基金資助項目(11FJPY01);福建省高等學校新世紀優秀人才支持計劃基金資助項目(2012-FJ-NCET-ZR01)。

柯良文(1988-),男,碩士研究生,主研方向:數據挖掘,個性化推薦算法;王 靖,副教授、博士。

2014-02-19

2014-03-15 E-mail:lwke1213@163.com

中文引用格式:柯良文,王 靖.基于用戶特征遷移的協同過濾推薦[J].計算機工程,2015,41(1):37-43.

英文引用格式:Ke Liangwen,Wang Jing.Collaborative Filtering Recommendation Based on User Feature Transfer[J]. Computer Engineering,2015,41(1):37-43.