基于自適應陷波濾波器的有源阻尼控制方法

王萍, 蔡蒙蒙, 王尉

(天津大學自動化學院智能電網教育部重點實驗室,天津300072)

基于自適應陷波濾波器的有源阻尼控制方法

王萍, 蔡蒙蒙, 王尉

(天津大學自動化學院智能電網教育部重點實驗室,天津300072)

LCL濾波器因具有良好的高頻衰減特性而被廣泛用作并網逆變器與電網的接口。弱電網情況下,并網模型中電網感杭值不可忽略,電網感杭的存在會影響LCL諧振頻率的大小,對傳統有源阻尼控制方法提出挑戰。在分析基于帶阻濾波器的有源阻尼控制方案基礎上,引入自適應陷波濾波器,提出了一種能夠跟隨系統參數變化自適應調整陷波濾波器負諧振點位置的有源阻尼控制方法。以光伏逆變系統為載體對該算法進行仿真分析,結果驗證了該方法在弱電網情況下的有效性和自適應性:系統諧振頻率發生偏移時該方法能夠實現對其的準確跟蹤,并且顯著降低諧振頻率點及附近頻率段的諧波含量;電網電壓發生±5%以內電壓突變時,該方法的動態響應特性仍能滿足系統的穩定運行要求。

弱電網;并網逆變器;有源阻尼控制;自適應控制;陷波濾波器

0 引 言

分布式發電系統(Distribution Power Generation Systems,DG)包括風力、光伏等新能源發電裝置,由于能夠在緩解能源危機的同時減少傳統化石燃料燃燒帶來的溫室氣體排放而得到大力推廣。分布式發電裝置等電力電子裝置越來越多地接人,向電網添加了大量非線性負載。另外,由于我國風力和光伏能源集中在西北部等較偏遠地區,遠距離的輸電線路不可避免地向電網引人線路阻抗。從而引發了電網諧波污染、電網電壓畸變等問題,嚴重影響電能質量,使電網的條件變得更加復雜。此時電網與電力二次裝置聯系較弱,即稱為弱電網。弱電網情況下的電網仿真模型不再是單純的穩壓交流電源,而應附加一個串聯的RL支路來等效代替［1］。

弱電網反過來也會對分布式電源與電網之間的逆變器裝置產生影響。文獻［2］指出,變化的電網阻抗給逆變器的穩定性、電流控制策略、LCL濾波器的參數設計以及有源阻尼控制方法的適用性等都帶來了挑戰,本文針對其中的有源阻尼控制方法進行了改善。

目前研究較多的有源阻尼控制方法可以分為以下幾類:第一類,單一電流環方案:基于濾波電容電流的有源阻尼反饋［3］、基于濾波電容電壓的有源阻尼反饋［4］以及基于濾波電容電壓的有源阻尼反饋［5］都屬于這一類;第二類,前向通路附加濾波器的方案:例如基于帶通濾波器有源阻尼控制［6］;第三類,基于降階模型的有源阻尼方案:這類方法中典型的應用有分裂電容電流控制法［7-8］;第四類,利用狀態反饋法進行閉環設計的方案:對多個狀態變量組合并進行加權計算,實現了特征方程的完全配置［9］。然而上述方法都是在LCL參數及電網感抗值唯一確定的情況下才能保證其有效性,弱電網情況下將失去其適應性［10］。

本文針對電網感抗變化帶來的諧振點偏移問題,采用自適應陷波濾波器作為突破點,提出了一種能夠自適應地改變控制參數,對電網感抗在一定范圍內變化的電網情況都有效的有源阻尼控制方法。第一部分對電網感抗與LCL諧振點的關系進行了具體闡述,第二部分分析了基于帶阻濾波器有源阻尼控制方法的機理及優缺點,第三部分介紹了自適應陷波濾波器的工作原理,驗證了自適應陷波濾波器取代傳統帶阻濾波器的可行性,第四部分包括系統的整體框圖和參數確認,第五部分仿真實驗。

1 電網阻抗對LCL諧振點的影響

為了說明電網感抗Lg對LCL諧振頻率點的影響,先根據圖1推導兩者關系。

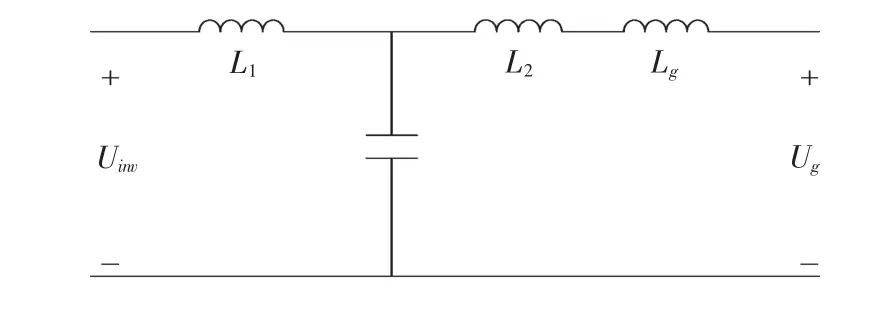
圖1 LCL濾波器拓撲Fig.1 Topology of LCL filter

圖1 所示,電網感抗的加人相當于在LCL網側串人一個附加電感,因此諧振頻率點的推導公式改寫為:

由式(1),Lg的變化將直接影響諧振頻率的大小,當Lg在0 mH到1.5 mH之間變化時,諧振頻率隨Lg變化的曲線如圖2所示。可知fres與Lg成負相關關系,fres隨Lg的增大而逐漸降低。

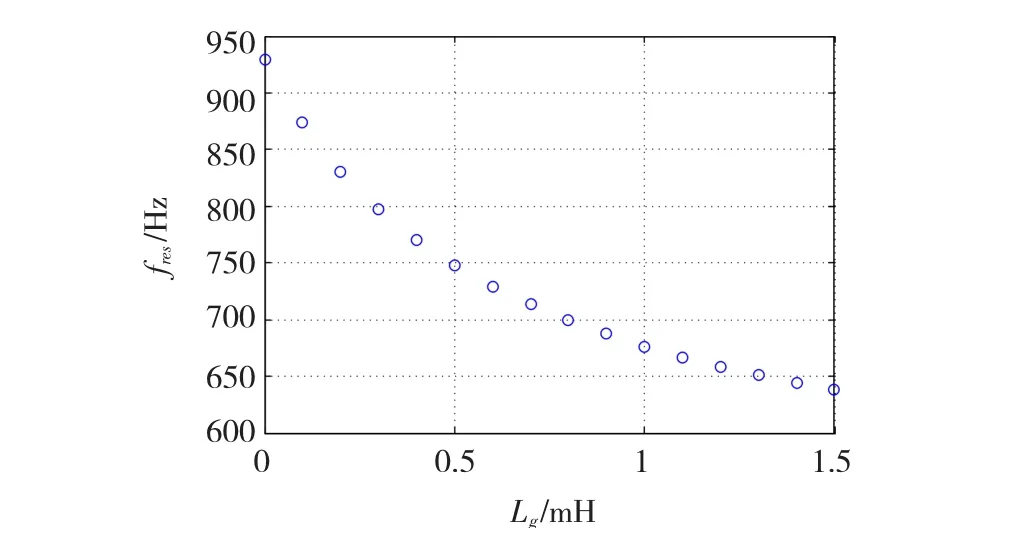
圖2 Lg與fres的關系曲線Fig.2 Relation curve between Lgand fres

2 基于帶阻濾波器的有源阻尼控制方法

LCL濾波器因對開關頻率以上高次諧波具有很好的抑制效果而被廣泛用作光伏并網逆變器與電網的接口,但它的存在同時增加了系統階數,帶來了諧振尖峰問題,對系統的控制策略提出了更加嚴格的要求。常用的抑制諧振增加系統阻尼的方法分為兩類:無源阻尼和有源阻尼控制方法。前者較為簡單,但會產生不必要的損耗,降低系統效率［11］,因此大功率光伏并網系統中通常采用有源阻尼控制方法。

常用的有源阻尼控制方法通過對含有諧振尖峰的環節G(s)添加一個H(s)反饋環節進行反饋校正實現［11］。

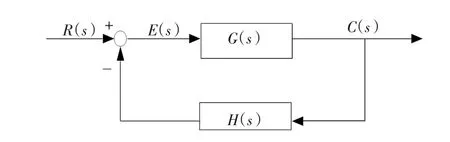
圖3 典型的反饋系統Fig.3 Typical feedback system

圖3 所示為典型反饋系統的控制原理,當反饋環節滿足諧振頻率附近處1+G(jωres)H(jωres)實部大于零,即可實現諧振尖峰的抑制。由于諧振頻率處網側電感、逆變器側電感以及濾波電容處的電流電壓信號相位變化范圍各不相同［12］,反饋信號所取不同時需采用的反饋環節也相應發生改變,以實現相位的超前滯后,最終使得1+G(jωres) H(jωres)在一、四象限范圍內。

然而,實際應用中通常需要考慮采樣延時和計算延時的影響(相當于在反饋環節中附加了慣性延遲環節),這些非理想因素雖然不會導致系統的失穩,但卻會影響有源阻尼控制的有效性。為避免此影響,本文考慮在前向通道G(s)中直接加人校正環節的有源阻尼控制方法。

具體控制框圖如圖4所示,參照文獻［6］所提出的基于帶通濾波器的有源阻尼控制方法,用帶阻濾波器來替代帶通濾波器實現同樣功能,在不額外增加傳感器的前提下,將帶阻濾波環節添加在調制波發生環節之前,實現一種基于帶阻濾波器的有源阻尼控制方法。

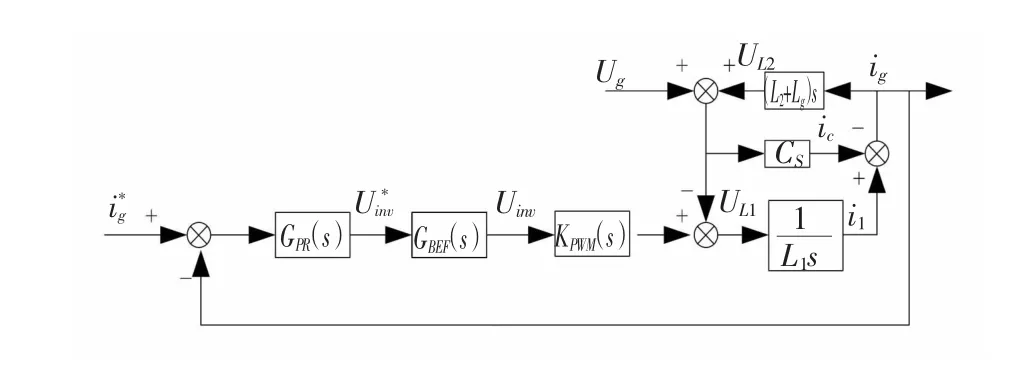
圖4 基于帶阻濾波器的有源阻尼方案Fig.4 Band-reject filter based active dam ping control strategy

從圖中可以看出,前向通道中原本經由PR電流調節器輸出的調制波U*inv,再通過帶阻濾波器的調節輸出最終的調制波Uinv,送給PWM波發生模塊。對電網側的電流進行采樣,再通過一個單位反饋構成閉環,就形成了整個控制策略。

由此可以推導出整個系統的開環傳遞函數:

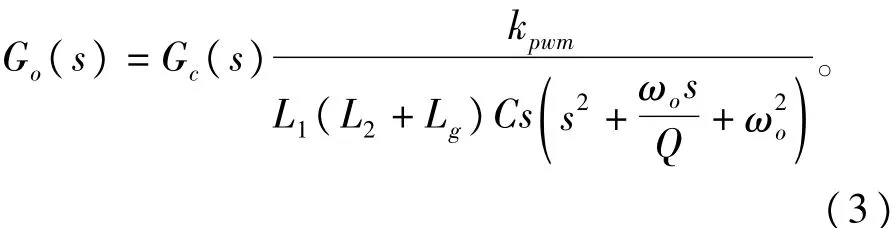
根據式(2)、式(3)繪制帶阻濾波器加人前后的系統開環波特圖,用作對比分析,如圖5所示。

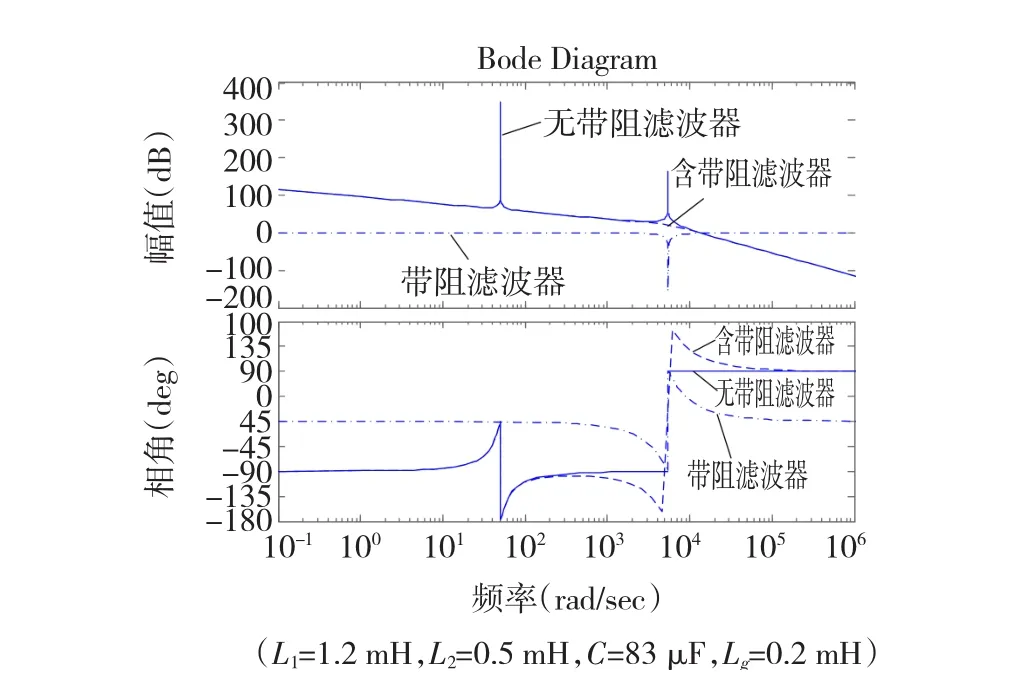
圖5 系統波特圖Fig.5 System bode plot

對比圖中三條曲線,可以看出,直線代表的沒有加人帶阻濾波環節的原系統波特圖中存在一個十分明顯的諧振尖峰,點劃線所示帶阻濾波器環節在同一頻率處產生了一個負的諧振尖峰,與之疊加使得原系統中的諧振尖峰得到抵消,由此,虛線所示加人帶阻濾波環節后的控制策略下的系統不再存在尖峰等不穩定因素。另外,如圖直線和點劃線所示,系統低頻和高頻開環增益受到帶阻濾波器的影響很微弱,可以忽略不計,說明了其引人并不會破壞LCL濾波環節對高頻信號的抑制效果,同時也保持了PR控制器對基頻信號的良好跟蹤效果。最后,從相位特性上看,原系統中由LCL環節引人的共軛極點所引發的諧振頻率處180°相位突變也得到了改善。

圖6為帶阻濾波器加人前后的系統閉環零極點分布圖。圖6(a)所示加人有源阻尼控制前系統具有分布在正半實軸的極點,說明此時系統是不能穩定的。加人帶阻濾波器后系統零極點分布如圖6(b)所示,原本給系統帶來不穩定因素的共軛極點進人負半軸區域,并且,從距離虛軸的位置可以看出,與主導極點相比,該極點的影響可以忽略不計。系統的主導極點在加人帶阻濾波器環節后沒有發生偏移,說明帶阻濾波器環節不會改變系統的動態響應速度以及阻尼特性。由此,本方法的有效性得到了理論上的支持。

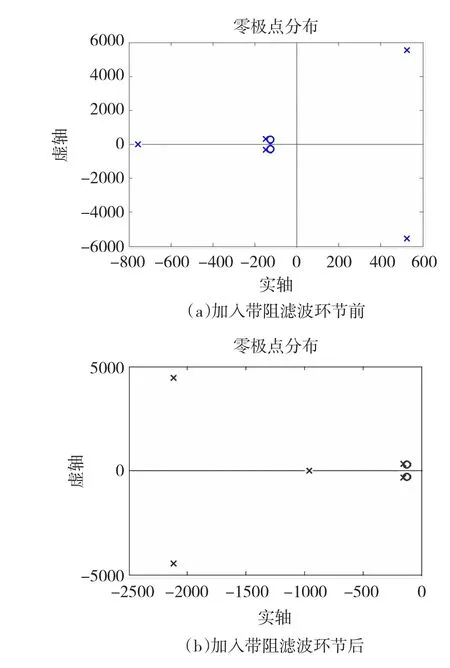
圖6 系統閉環零極點分布Fig.6 System zero-pole distribution

保持PR控制器參數以及GBEF參數不變,Lg取值變化為0.3mH,系統波特圖有所改變,如圖7所示。

圖7 Lg參數發生改變時的系統波特圖Fig.7 System bode p lot w ith a changed Lgvalue

圖中原系統中的諧振尖峰發生偏移,不能被帶阻濾波器產生的負諧振尖峰抵消,有源阻尼控制失效。因此傳統基于帶阻濾波器的有源阻尼控制方法存在其局限性。

光伏逆變器接人點的改變必然會引起等效電網感抗值的變化,并且,隨著分布式發電系統越來越多的接人到電網當中,同一接人點的電網感抗值也不是一成不變的,因此,構建一種能夠適應一定范圍內電網感抗變化的有源阻尼控制方法十分重要。

3 自適應陷波濾波器

上節提到電網感抗發生改變時,傳統基于帶阻濾波器的有源阻尼控制方法失去適應性,因而這里考慮引人在聲學去噪領域應用廣泛的自適應陷波濾波器,用它來代替傳統帶阻濾波環節,實現隨諧振點偏移而自適應調節參數的有源阻尼控制方法。

下面介紹自適應陷波濾波器的基本工作原理,參照圖8進行分析［13］。

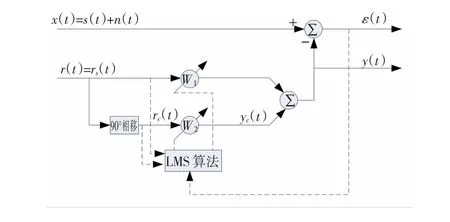
圖8 自適應陷波濾波器原理Fig.8 W orking princip le for adaptive notch filter

圖中x(t)為輸人信號,即疊加有干擾信號的原始信號,s(t)為目標信號,n(t)為需要濾除的干擾信號,rs(t)=A sinωot為參考信號,是一個同干擾信號相關的純正弦信號,參考信號90°相移后得到rc(t),rc(t)與rs(t)進行加權運算得到y(t),ε(t)為自適應陷波濾波器的輸出信號,也就是對原始信號特定頻率諧波濾除后的信號,其值等于原始信號x(t)與加權值y(t)的差。

LMS模塊的作用是對加權值W1、W2進行迭代更新,其中rs(t)、rc(t)、ε(t)作為輸人信號輸人到LMS算法模塊中,W1(t)、W2(t)作為模塊的輸出,內部采用最小均方的迭代算法(LMS算法),目的是使誤差信號ε(t)的功率ε2(t) 趨于極小值,套用文獻［14］中的公式,權函數迭代方法如下:

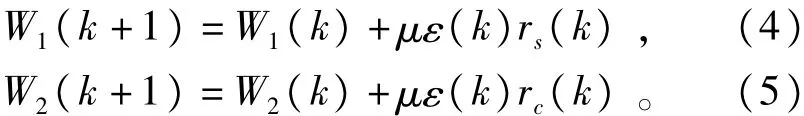
其中μ代表自適應迭代步長,k為與時間相關的迭代序列,并有t=kτ,τ為采樣時間間隔。

文獻［14］同時推導出了自適應陷波濾波器的等效傳遞函數,表達式如下:

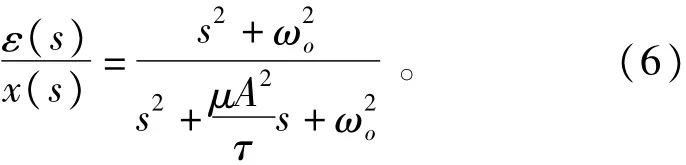
對比發現式(6)與前文所介紹帶阻濾波器的傳遞函數具有相同形式,對頻率為ωo/2πHz的信號同樣具有無窮大衰減功能,令μA2/τ=ωo/Q,則自適應陷波濾波器可以完全等效為中心頻率ωo的帶阻濾波器。與帶阻濾波器類似,μA2取值越大,相應的品質因數就越小,系統的帶寬就越大。因此可以通過優化μA2的取值來改善陷波濾波器的響應特性。由于自適應陷波濾波器的中心頻率即參考信號頻率易于更改,改變參考信號頻率可靈活地對陷波濾波器的中心頻率進行調整,實現濾波器在干擾信號頻率改變時的自適應性,因此能夠滿足一定變化范圍電網感抗條件下的有源阻尼控制要求。

4 總體系統框圖及參數設置

4.1 總系統框圖

上文給出了一種基于帶阻濾波器的有源阻尼控制方法,同時證明了采用自適應陷波濾波器代替帶阻濾波器可以實現有源阻尼控制的自適應性。

在此基礎上,可以得出本文的最終控制策略——基于自適應陷波濾波器的有源阻尼控制方法。總體控制框圖如圖9所示,這里電流環采用準PR控制方法。

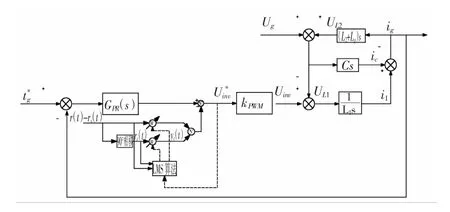
圖9 基于自適應陷波濾波器的有源阻尼控制方案Fig.9 Adaptive notch filter based active damping control system fram ework

4.2 自適應濾波器參數設置

為了更好地實現并網電流跟蹤及有源阻尼控制的效果,下面對控制器參數的選取方法進行簡要分析。由于本文主要研究對象為自適應陷波控制器,因而準PR控制器參數的選取在這里不作為重點,下文針對自適應陷波濾波器的主要參數:收斂因子μ、迭代步長τ進行說明。

首先分析迭代步長τ對系統動態響應速度的影響。為觀察方便,我們可以將目標信號設置為諧波成分較為簡單的:s(t)=sin(2πt)+sin(2π×2t)+ sin(2π×5t),疊加上n(t)=0.1cos(2π×50t)的干擾信號后作為原始信號輸人到自適應陷波濾波器中,改變τ值,觀察不同步長τ下系統的響應結果,如圖10和圖11所示,分別對應了τ=3×10-4s(圖10)以及τ=3×10-3s(圖11)時的系統。仔細觀察可以發現圖11中的輸出信號比圖10中的收斂要慢,收斂時間更長。由此可以得出步長越短,收斂速度越快的結論。然而為減小自適應迭代權噪聲,步長的選取又不能過分小,本實驗選取τ=1×10-5s。

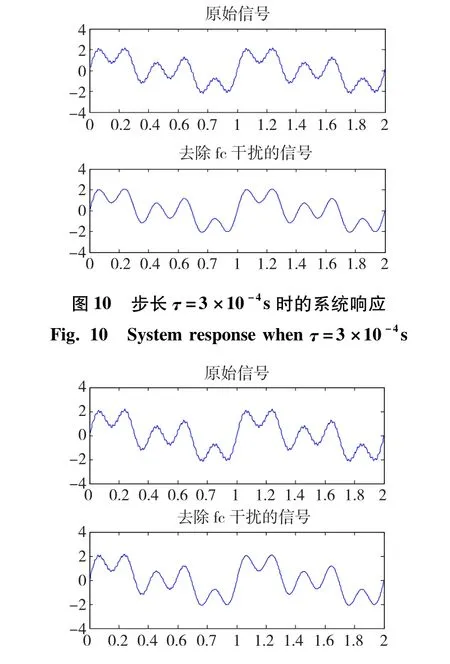
圖11 步長τ=3×10-3s時的系統響應Fig.11 System response whenτ=3×10-3s

確定了τ的取值后,下面分析迭代因子μ的選取原則,圖12、圖13分別給出了不同μ值下的系統開環波特圖及階躍響應曲線,反映了μ值的選取對系統動靜態特性的影響。圖12所示,各μ值下的系統低頻段和高頻段開環幅相曲線基本重合,只在諧振頻率附近存在差異。并且μ值越大,開環增益越小,帶寬越寬,對諧振頻率點及附近諧波含量的抑制效果也越明顯,因此可以推斷出μ值越大,諧振頻率點發生微小偏移時的有源阻尼控制效果就越能得到保證。然而,如圖13所示,當μ=0.01或0.008時,系統的單位階躍響應雖能收斂,但卻出現了疊加的新低次諧波,這個現象說明μ的取值也并非越大越好。當μ分別取為0.02、0.03、0.05、0.08時,系統單位階躍響應的超調量逐漸增大,收斂速度卻沒有太大的差別。因此,這里選取超調量較小且不會給系統引人新諧波的0.02作為收斂因子μ的取值。

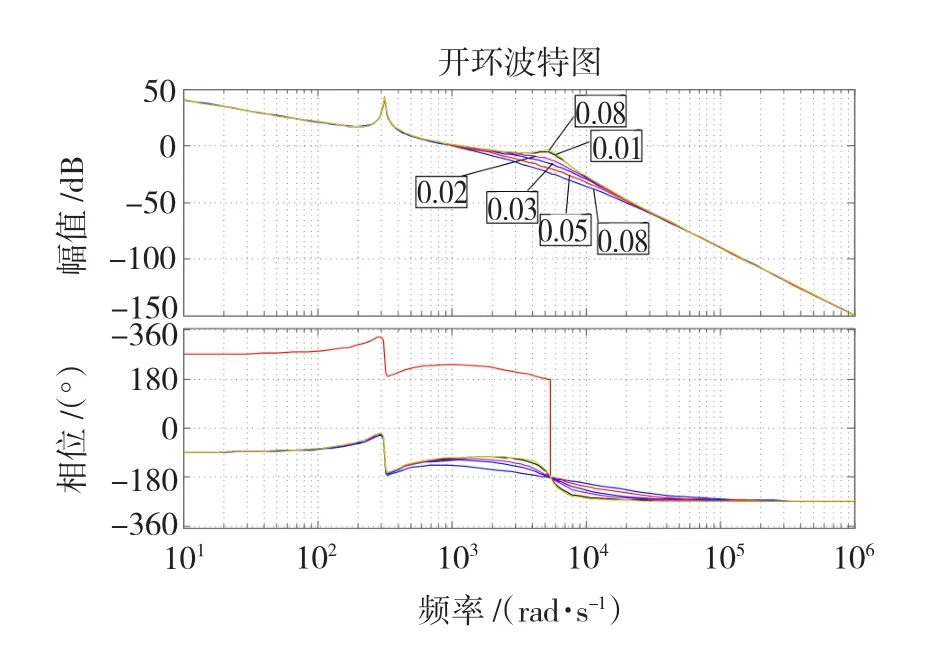
圖12 不同μ值下的系統開環波特圖Fig.12 System open loop bode plot under differentμvalue

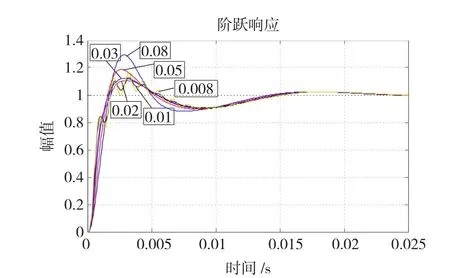
圖13 不同μ值下的系統階躍響應Fig.13 System step respond under differentμvalue

這樣τ,μ,A的取值都得到了唯一的確定,但是回過頭再來考慮該等式μA2/τ=ωo/Q時,卻會發現一個問題:若保持τ,μ,A的取值不變,當ωo因為弱電網特性下等效電網感抗的改變而發生偏移時,為保證系統的Q值不變,τ,μ,A的取值也應該做同比例放大或縮小。因此選擇上述仿真中對應的ωref= 133作為基準頻率,令kω=ωo/ωref,仍然忽略τ,A對系統動靜態特性的影響,在自適應調整陷波濾波器中心頻率ωo的同時調整μ的取值為kωμ。由此附加有參數自適應校正環節的總系統有源阻尼控制方案唯一確定,具體的參數校正實現由LMS算法的軟件編程完成。

5 仿真驗證

上文確定了系統的整體控制框圖及參數,下面通過Matlab/SIMULINK平臺搭建7kVA光伏逆變系統仿真模型以驗證本文所提方法的有效性。圖14給出了系統拓撲結構。

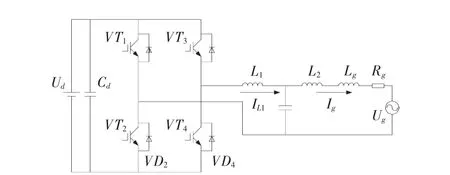
圖14 光伏并網逆變器拓撲Fig.14 PV grid-connected inverter system topology

系統參數設置參照表1,其中PWM波形的發生采用雙極性調制方法,自適應陷波濾波器中的LMS算法模塊通過自定義編寫S-function模塊實現。按照表1的參數進行仿真設置,得出如圖15所示的仿真結果。

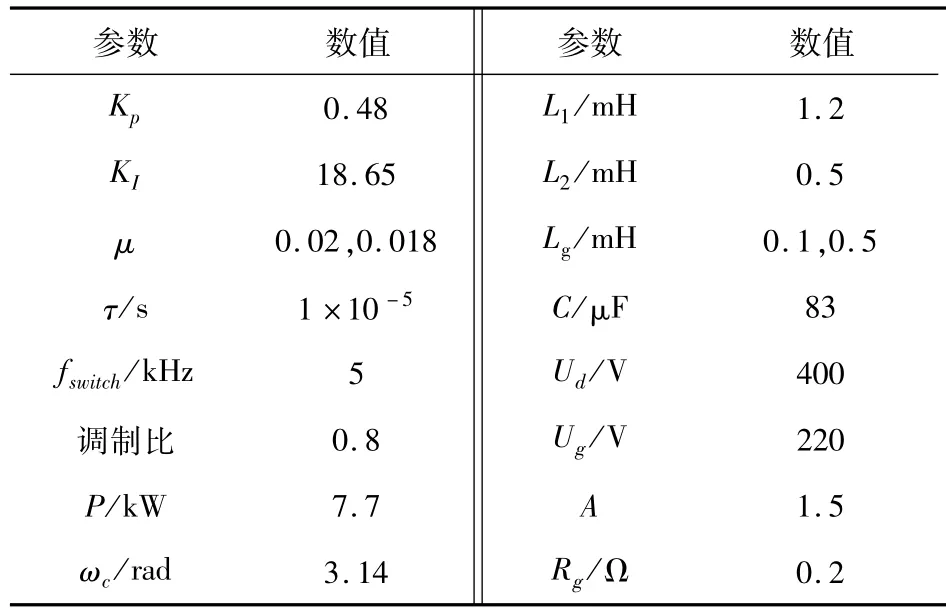
表1 系統參數Table 1 System parameters

圖15(a)中并網電流在3/4個基波周期后跟蹤上電網電壓相位,并一直保持了對電網相位的跟隨,滿足了逆變器并網單位功率因數運行的要求。圖15(b)為逆變器直接輸出的逆變器側電感電流,其波形相較于圖15(a)明顯多出大量開關頻率次諧波,對比兩圖,又可以驗證LCL濾波器對高次諧波的優良的抑制效果。

為充分驗證該方法的有效性及自適應性,本文選取了兩組不同控制條件下的并網電流FFT數據結果,并進行對比分析:第一組通過對比自適應陷波濾波器加人前后系統并網電流中諧振頻率諧波含量的大小,驗證了其有效性;第二組則通過對比電網感抗發生改變情況下傳統基于帶阻濾波器的有源阻尼控制方法及基于自適應陷波濾波器的有源阻尼控制方法的有效性,驗證了其自適應性。

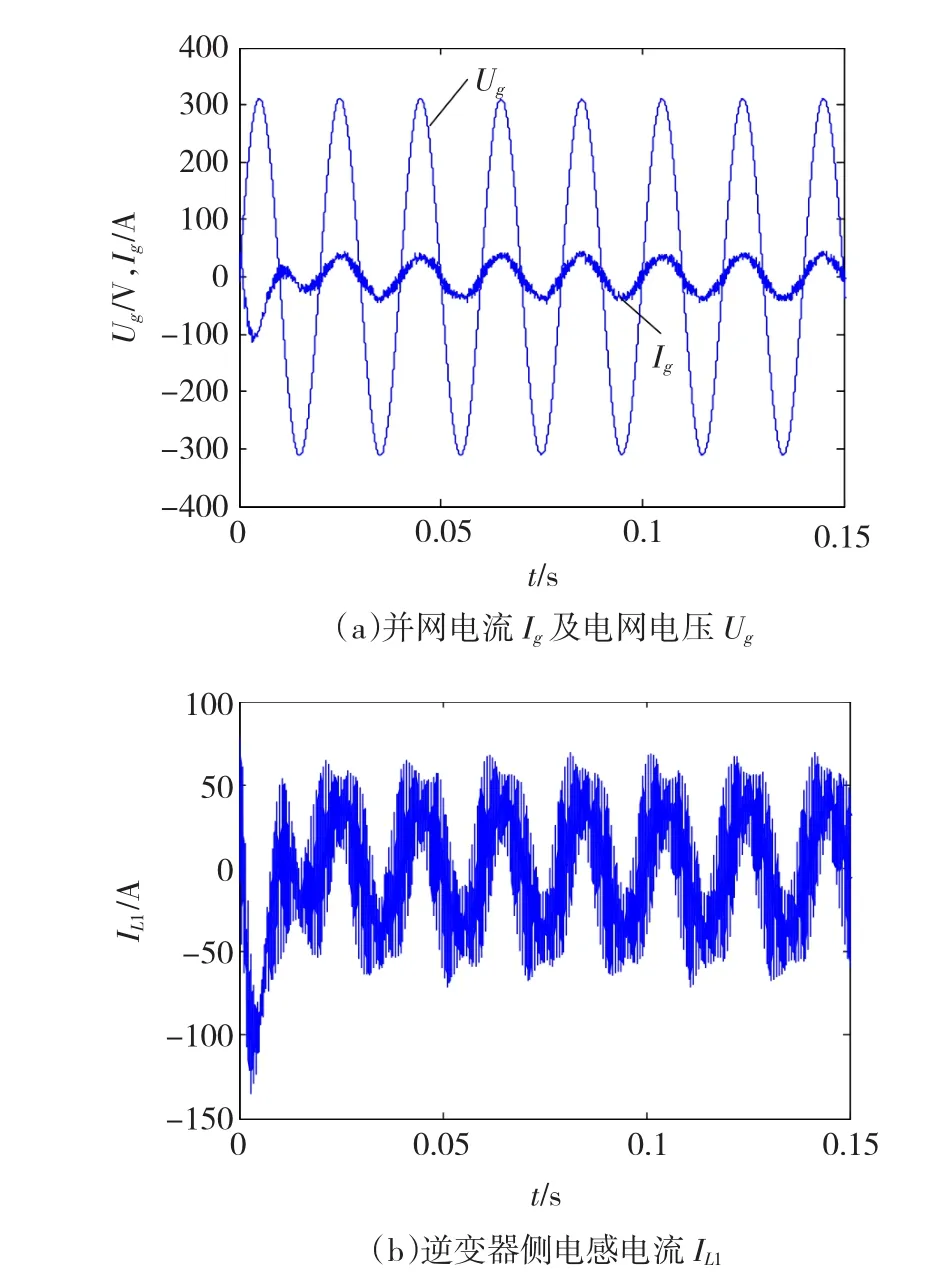
圖15 并網電流Ig的跟蹤效果以及LCL濾波器濾波效果Fig.15 Tracking accuracy of the current Igand LCL filter filtering effect IL1

5.1 有效性驗證

圖16、圖17分別為加人自適應陷波濾波器有源阻尼控制模塊前后的系統并網電流頻譜分析圖,對比可知,系統諧振頻率(873.48 Hz)處以及附近頻率的諧波含量在采用該有源阻尼控制方法后大幅下降。同時表2列出了兩種情況下的具體諧波含量值,對比也可以看出該方法對諧振頻率附近的諧波具有明顯抑制效果,從而驗證了該方法的有效性。

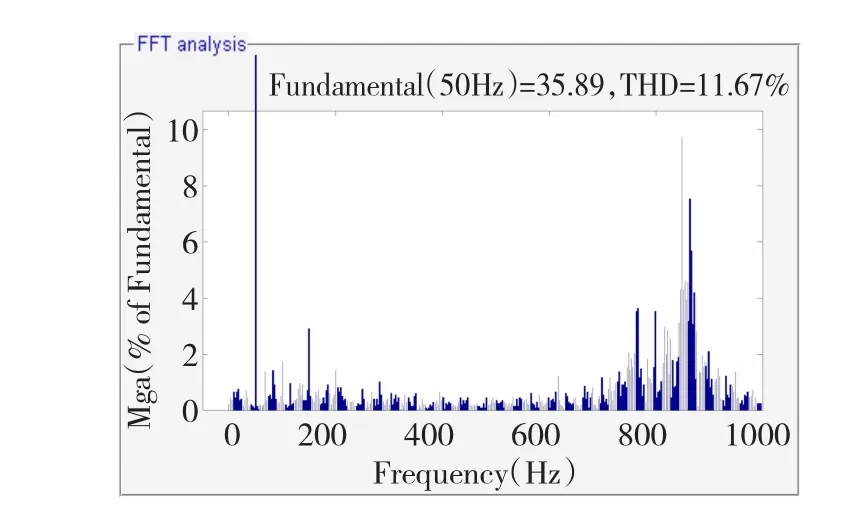
圖16 并網電流IgFFT(無有源阻尼)Fig.16 Grid-connected current IgFFT(w ithout adopting active dam ping control)

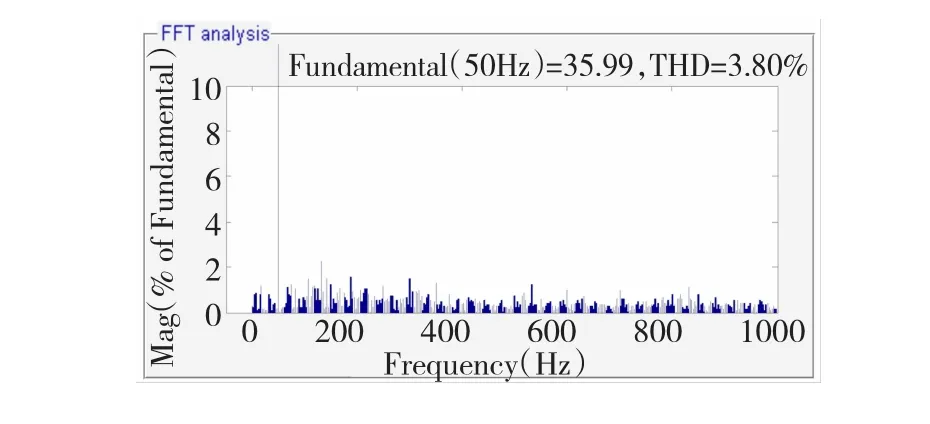
圖17 并網電流IgFFT(含自適應有源阻尼)Fig.17 G rid-connected current IgFFT(adopting active damping control)

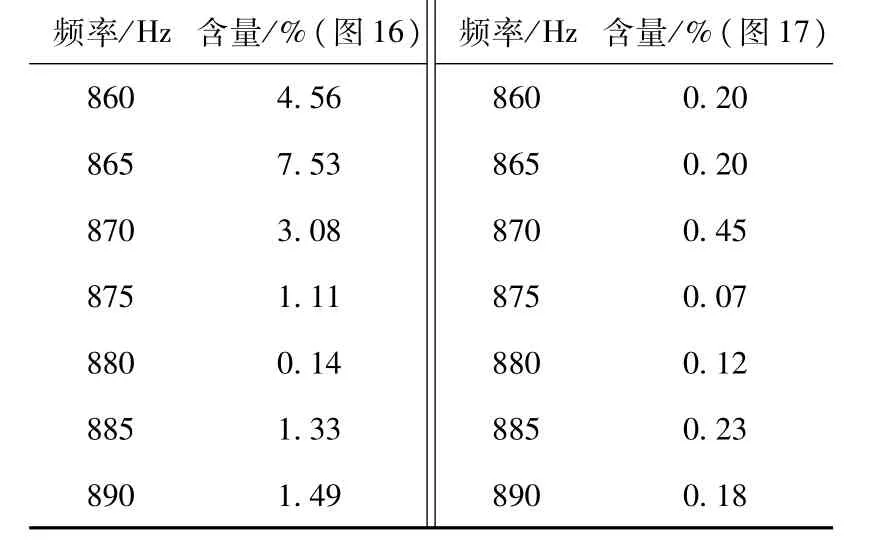
表2 諧波含量對比Table 2 Harm onic contents com parison

5.2 自適應性驗證

改變系統參數,使Lg從0.1 mH變化為0.5 mH,理論推導得出此時的系統諧振尖峰應偏移到748 Hz處。分別觀察無有源阻尼控制方法,傳統有源阻尼控制方法以及自適應陷波濾波器有源阻尼控制方法的控制效果。仍采用對并網電流諧振頻率附近含量的抑制效果來衡量控制方法的有效性,得出圖18～圖20所示結果,分別表示無阻尼控制,傳統阻尼控制,以及自適應有源阻尼控制結果。為更清晰地對比圖19、圖20的仿真效果,將圖19與圖20所對應具體諧波含量的數值表示列于表3中。

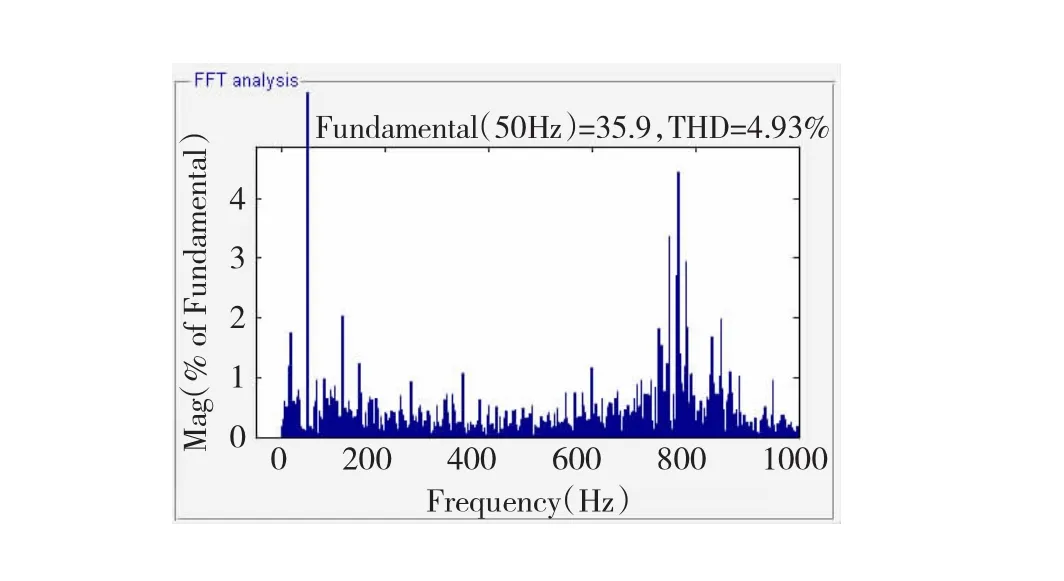
圖18 無有源阻尼控制仿真結果Fig.18 Control result w ithout adopting active damping

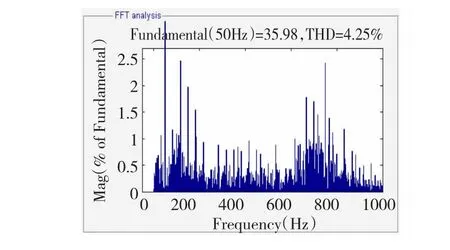
圖19 傳統有源阻尼控制仿真結果Fig.19 Control resu lt w ith traditional active dam ping

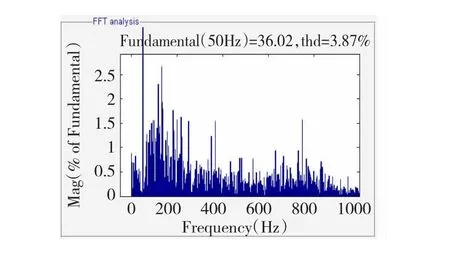
圖20 自適應有源阻尼控制仿真結果Fig.20 Control result w ith adaptive active dam ping

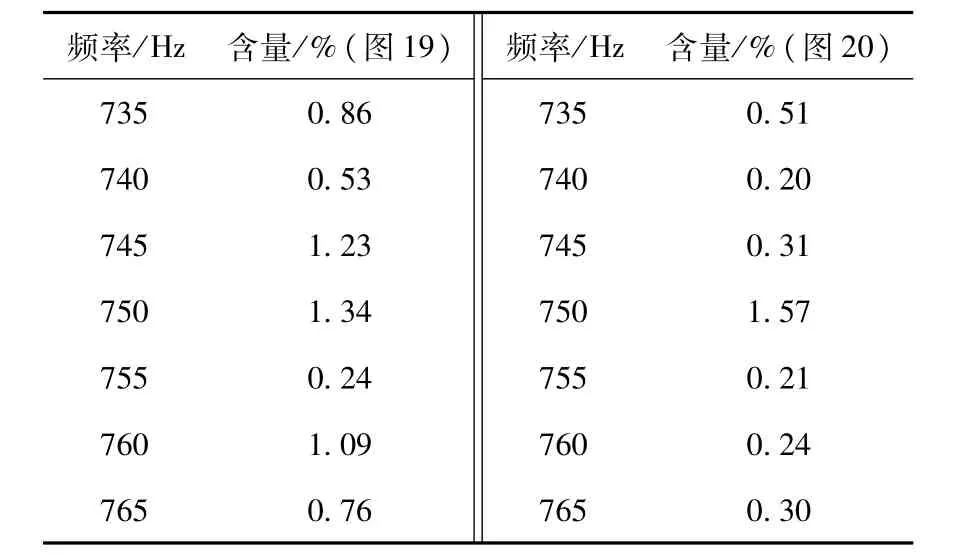
表3 諧波含量對比Table 3 Harmonic contents comparison

對比圖18與圖16不難發現,電網電感值的波動導致了系統諧振尖峰的偏移,新的諧振被顯示于748 Hz附近頻率段,呼應了前文電網感抗對電網電流高頻段影響的分析。

縱向對比完圖18、圖16對應兩組電網感抗值下的系統響應后,再來對比分析電網感抗發生變動時兩種控制方法的諧振抑制效果,即驗證傳統有源阻尼控制方法及自適應有源阻尼控制方法的自適應性。

首先可以肯定的是,圖19及圖20中748 Hz附近的諧波含量相較圖18都存在明顯下降,而圖19中748 Hz附近的諧振含量仍然高于其他頻率,呈現出較弱的諧振現象。相較之下,圖20中748 Hz附近頻率段的諧波含量下降趨勢更為突出,下降后基本與其他頻率段持平,諧振尖峰完全消除。表3中的實驗數據也再次支持了這一實驗結果,佐證了自適應有源阻尼控制方法較傳統有源阻尼控制方法具備對新諧振尖峰更突出的抑制效果。

綜上所述自適應控制算法能夠在電網參數發生變化時及時調整自身參數從而表現出更為優越的性能,而傳統阻尼控制方法則不具備這一自適應特性。

5.3 電網條件突變時的系統動態響應特性

驗證完基于自適應陷波濾波器有源阻尼控制方法的有效性和自適應性能之后,分兩種情況來考察自適應控制方法的動態響應特性:第一種是電網電感發生瞬時突變的情況,第二種是理想電網負載突變的情況。設置0.1 s時刻,電網電感由0.1mH變化為0.5mH,得出相對應輸出并網電流的波形如圖21所示。

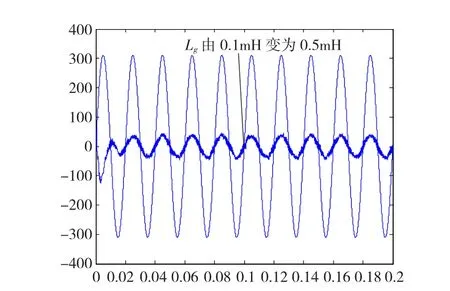
圖21 電網感抗突變下的動態響應Fig.21 Dynam ic response w ith a sudden im pedance change

由圖21可知,系統參數突變時,自適應有源阻尼控制可以迅速做出調整并達到穩定收斂的結果,調整過程當中并不會導致失穩或超調現象,證明了自適應有源阻尼控制方法良好的動態響應特性。

下面再來考慮電網負載突變的情況,實際電網電壓運行的最大變動范圍為±5%,因此這里將電網電壓做如下設置:0.1 s時由220 V跳變成231 V,0.2 s時由231 V越變為209 V。如果系統能夠滿足該條件下的電網負載波動,則電網的正常運行要求也能得以滿足,仿真結果如圖22所示。

如圖22所示,隨著電網電壓的波動,并網電流整體保持穩定,僅在0.1 s及0.2 s時刻后的半個周期內存在小幅波動,但是波動范圍很小,動態響應過程較短,能夠滿足系統穩定性的要求,對電網造成的不良影響基本可以忽略。

綜上所述,在電網參數發生突變時,本文提出的基于自適應陷波濾波器的有源阻尼控制方法能夠同時滿足系統的動穩態特性要求。

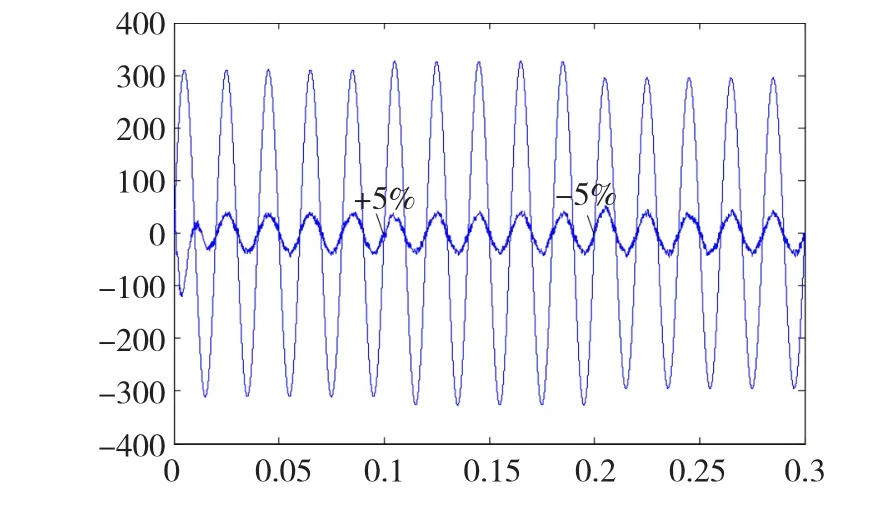
圖22 電網負載波動下的動態響應Fig.22 Dynam ic response w ith a sudden grid-voltage change

6 結 論

本文分析了光伏逆變系統中電網感抗對于LCL諧振點的影響,在基于帶阻濾波器的有源阻尼控制方法基礎上,引人自適應陷波濾波器,提出了一種能夠跟隨電網感抗值變化自適應調整控制參數的有源阻尼控制方法,分析了其控制機理,并通過7kVA的光伏逆變系統仿真模型驗證了該方法的有效性及自適應性,得出了如下結論:

1)隨著電網感抗值的波動,LCL諧振頻率呈負相關變化;

2)自適應陷波濾波器能夠代替帶阻濾波器實現衰減特定頻譜段波形的作用;

3)自適應陷波濾波器的參數τ與收斂速度相關,參數μ與系統帶寬以及動態響應的收斂性相關;

4)該基于自適應陷波濾波器的有源阻尼控制方法能夠很好的滿足弱電網情況下的動穩態響應要求。

該有源阻尼控制方法原理簡單,但是需要以對電網感抗值的準確測量為前提,額外增加了電網感抗在線測量的技術成本。但其控制結構簡單,容易實現,并且提高了電網的適應性,具有一定的應用前景和發展空間。

［1］ 魯力,劉芳,張興,等.弱電網條件下單相光伏并網逆變器的控制研究［J］.電力電子技術,2012,46(5):36-38. LU Li,LIU Fang,ZHANG Xing,etal.Study of controlling a single-phase photovoltaic grid-connected inverter operating in a weak grid［J］.Power Electronics,2012,46(5):36-38.

［2］ LISERRE M,TEODORESCU R,BLAABJERG F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set ofgrid impedance values［J］.IEEE Transactionson Power E-lectronics,2006,21(1):263-272.

［3］ 王斯然,呂征宇.LCL型并網逆變器中重復控制方法研究［J］.中國電機工程學報,2010,30(27):69-75. WANG Siran,LüZhengyu.Research on repetitive controlmethod applied to grid-connected inverterwith LCL filter［J］.Proceedings of the CSEE,2010,30(27):69-75.

［4］ TWINING E,HOLMESD G.Grid current regulation of a threephase voltage source inverter with an input LCL filter［J］.IEEE Transactions on Power Electronics,2003,18(3):888-895.

［5］ MALINOWSKIM,BERNET S.A simple voltage sensorless active damping scheme for three-phase PWM converters with an LCL filter［J］.IEEE Transactions on Industrial Electronics,2008,55 (4):1876-1880.

［6］ 尹靖元,金新民,吳學智,等.基于帶通濾波器的LCL型濾波器有源阻尼控制［J］.電網技術,2013,37(8):2376-2382. YIN Jingyuan,JIN Xinmin,WU Xuezhi,et al.Active damping control strategy for LCL filter based on band pass filter［J］.Power System Technology,2013,37(8):2376-2382.

［7］ SHEN Guoqiao,XU Dehong,CAO Luping,et al.An improved control strategy for grid-connected voltage source inverters with an LCL filter［J］.IEEE Transactions on Power Electronics,2008,23(4):1899-1906.

［8］ 沈國橋,徐德鴻.LCL濾波并網逆變器的分裂電容法電流控制［J］.中國電機工程學報,2008,28(18):36-41. SHEN Guoqiao,XU Dehong.Current control for grid-connected inverters by splitting the capacitor of LCL filter［J］.Proceedings of the CSEE,2008,28(18):36-41.

［9］ GABE IJ,MONTAGNER V F,PINHEIROH.Design and implementation of a robust current controller for VSI connected to the grid through an LCL filter［J］.IEEE Transactions on Power Electronics,2009,24(6):1444-1452.

［10］ YANG Shuitao,LEIQin,PENG F Z,et al.A robust control scheme for grid-connected voltage-source inverters［J］.IEEE Transactions on Industrial Electronics,2011,58(1):202-212.

［11］ 郭小強,鄒偉揚,顧和榮,等.并網逆變器LCL接口直接輸出電流控制建模及穩定性分析［J］.電工技術學報,2010,25 (3):102-109. GUO Xiaoqiang,WU Weiyang,GU Herong,et al.Modelling and stability analysis of direct output current control for LCL interfaced grid-connected inverters［J］.Transactions of China Electrotechnical Society,2010,25(3):102-109.

［12］ 許津銘,謝少軍,肖華鋒.LCL濾波器有源阻尼控制機制研究［J］.中國電機工程學報,2012,32(9):27-33. XU Jinming,XIE Shaojun,XIAO Huafeng.Research on control mechanism of active damping for LCL filters［J］.Proceedings of the CSEE,2012,32(9):27-33.

［13］ 惠俊英,蔡平,馬曉民.自適應陷波濾波器的應用研究［J］.聲學學報,1991,16(1):19-24. HUIJunying,CAI Ping,MA Xiaomin.Applied study of active notch filter［J］.Acta Acustica,1991,16(1):19-24.

［14］ 常建華,全書海.自適應濾波器的原理、應用及其算法仿真［J］.武漢汽車工業大學學報,1998,20(3):46-49. CHANG Jianhua,QUAN Shuhai.Algorithm,principle and computer simulation of the adaptive filter wave trap［J］.Journal of Wuhan Automotive Polytechnic University,1998,20(3):46 -49.

(編輯:張詩閣)

Adaptive notch filter based active damping controlmethod

WANG Ping, CAIMeng-meng, WANGWei
(Smart Grid Key Laboratory of Education Ministry,Electrical Engineering and Automation Department,Tianjin University,Tianjin 300072,China)

The LCL filter iswidely applied as interface between grid-connected inverter and grid due to a preferable high frequency attenuation characteristic.In the condition of weak grid,impedance value of grid model cannot be ignored,and the existence of grid impedance results in different LCL resonant frequencies,which challenges traditional active damping control.Based on the analysis of band pass filter based active damping control strategy,an adaptive active damping control was proposed by introducing the application of active notch filter,which can adjust the position of negative resonance point adaptively so as tomanage sudden grid changes.Theoretical analysis and simulation results presented on the platform of grid-connected PV inverter system indicate the effectiveness and adaptability of this active damping strategy:deviation of system resonance point is correctly traced,besides,harmonic contents of the resonance point and nearby frequency bands is significantly reduced.In addition,system stability can be ensured by the rapid dynamic response characteristic when there is a voltage leap within±5%.

weak grid;grid-connected inverter;active damping control;self-adaptation control;notch filter

10.15938/j.emc.2015.09.016

TP 13

A

1007-449X(2015)09-0108-09

2014-04-03

高等學校博士學科點專項科研基金(20120032110070)

王 萍(1959—),女,教授,博士生導師,研究方向為電力電子變換術及其控制、智能檢測與控制、電子電路與系統;蔡蒙蒙(1990—),女,碩士研究生,研究方向為光伏并網逆變器及其控制;王 尉(1990—),男,碩士研究生,研究方向為電力電子變換技術。

蔡蒙蒙