高超聲速數(shù)值模擬平臺轉(zhuǎn)捩模型的標定

張毅鋒，雷凈，張益榮，毛枚良，陳堅強

高超聲速數(shù)值模擬平臺轉(zhuǎn)捩模型的標定

張毅鋒1，雷凈2，張益榮1，毛枚良1，陳堅強1

(1.中國空氣動力研究與發(fā)展中心計算空氣動力研究所，四川綿陽621000; 2.北京臨近空間飛行器系統(tǒng)工程研究所，北京100076)

基于CARDC的高超聲速流動數(shù)值模擬軟件平臺Chant-2.0，以典型低速平板轉(zhuǎn)捩算例為參考，對γ-Reθ轉(zhuǎn)捩模型的經(jīng)驗關(guān)系式進行了標定，并且對壓力梯度函數(shù)進行了高馬赫數(shù)修正，在高超平板和尖錐的轉(zhuǎn)捩算例中進行了初步檢驗，計算結(jié)果表明:在高超計算平臺上標定的轉(zhuǎn)捩模型，較好地模擬了低速平板流動的轉(zhuǎn)捩起始位置和轉(zhuǎn)捩區(qū)長度，經(jīng)過高馬赫數(shù)修正后在高超流動轉(zhuǎn)捩模擬中表現(xiàn)出較大的潛力。

高超聲速流動;數(shù)值模擬;轉(zhuǎn)捩模型;標定

0 引言

Menter等根據(jù)低速平板轉(zhuǎn)捩風(fēng)洞試驗，在2002年提出了一種可避免非局部信息的γ-Reθ轉(zhuǎn)捩模型［1-4］，該模型沒有考慮轉(zhuǎn)捩過程的物理機理，而是依據(jù)風(fēng)洞實驗數(shù)據(jù)將局部湍流度和壓力梯度等物理量與轉(zhuǎn)捩動量厚度雷諾數(shù)相關(guān)聯(lián)，根據(jù)局部渦量雷諾數(shù)和臨界動量厚度雷諾數(shù)的比值判斷轉(zhuǎn)捩，在流場中任意一個渦量雷諾數(shù)超過局部轉(zhuǎn)捩雷諾數(shù)的地方，間歇方程源項被激活并產(chǎn)生湍流。該模型優(yōu)點是:嚴格意義上基于局部變量的轉(zhuǎn)捩模型，與現(xiàn)代CFD方法兼容，如非結(jié)構(gòu)網(wǎng)格和大規(guī)模并行計算，可以方便地融于一般數(shù)值模擬軟件中。目前，γ-Reθ模型已經(jīng)被成功地用于低速翼型、航空器和渦輪流動的轉(zhuǎn)捩數(shù)值模擬中［1-5］。

γ-Reθ轉(zhuǎn)捩模型包含三個關(guān)鍵的經(jīng)驗關(guān)系式:轉(zhuǎn)捩動量厚度雷諾數(shù)Reθt、轉(zhuǎn)捩區(qū)長度Flength、臨界動量厚度雷諾數(shù)Reθc。Reθt關(guān)系式是通過低速平板試驗得到的Reθt和局部湍流度、壓力梯度參數(shù)的關(guān)系建立的。Menter和Langtry等最初僅給出了Reθt經(jīng)驗關(guān)系式，而Flength和Reθc的具體形式則被作為商業(yè)秘密直到2009年才在文獻［2］中公開。實際上，由于各種CFD計算平臺的數(shù)值特性不同，F(xiàn)length和Reθc的具體形式和參數(shù)會有所不同，例如Srensen［6］、Suluksna［7］、Martin［8］、張玉倫［9］、牟斌［10］等分別采用不同的經(jīng)驗關(guān)系式也都較好地模擬了T3系列低速平板轉(zhuǎn)捩，而為了得到理想的計算結(jié)果通常需要在所用計算平臺上進行細致的數(shù)值標定。

鑒于γ-Reθ模型在低速流動轉(zhuǎn)捩模擬中的成功，如何將該模型用于高超聲速流動的轉(zhuǎn)捩模擬正在吸引眾多學(xué)者研究，例如，Martin等(2008)［8］考慮來流湍流度構(gòu)造了Flength和Reθc關(guān)系式，較好地模擬了M∞=8.3的雙楔壁面壓力分布。Gray等(2009)［11］對壓力梯度和轉(zhuǎn)捩長度關(guān)系式進行修正，對M∞=8的尖錐進行了軸對稱計算，研究了來流湍流度和網(wǎng)格間距對轉(zhuǎn)捩模擬結(jié)果的影響。Khalil等(2012)［12］模擬了軸對稱高超圓錐轉(zhuǎn)捩流動，轉(zhuǎn)捩區(qū)熱流和實驗值符合較好。國內(nèi)，張曉東(2010)［13］、顏培剛(2011)［14］等也進行了類似的數(shù)值模擬。

本文以CARDC自主研發(fā)的高超聲速數(shù)值模擬軟件平臺Chant-2.0為基礎(chǔ)，采用γ-Reθ轉(zhuǎn)捩模型和kω SST湍流模型，通過T3系列低速平板數(shù)值試驗標定了γ-Reθ模型的Reθc和Flength經(jīng)驗關(guān)系式，并對轉(zhuǎn)捩模型了進行壓力梯度函數(shù)的高馬赫數(shù)修正，在M∞= 4.5平板和M∞=7.93的尖錐轉(zhuǎn)捩流動模擬中進行了初步驗證，計算結(jié)果表明，高馬赫數(shù)修正后的轉(zhuǎn)捩模型較好地預(yù)測了高速邊界層轉(zhuǎn)捩位置，適合高超聲速邊界層流動轉(zhuǎn)捩的模擬，值得進一步探討γ-Reθ模型在工程實際中的應(yīng)用。

1 模型簡介

γ-Reθ轉(zhuǎn)捩模型由兩個變量輸運方程構(gòu)成:間歇因子γ方程和當?shù)剞D(zhuǎn)捩起點動量厚度雷諾數(shù)珘Reθt方程。γ表示流動處于湍流和層流的時間比例，γ方程用來觸發(fā)當?shù)剞D(zhuǎn)捩，珘Reθt方程用來捕捉湍流強度的非局部影響和避免經(jīng)驗關(guān)系式中所用物理量帶來的非局部計算。珘Reθt方程是γ-Reθ模型的核心，它起到將經(jīng)驗公式和間歇方程中轉(zhuǎn)捩起點標準相聯(lián)接的作用。輸運方程的無量綱形式如下:

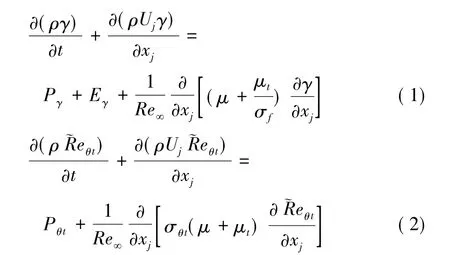
其源項及系數(shù)具體見文獻［2］。

γ-Reθ模型包含三個關(guān)鍵的經(jīng)驗關(guān)系式:轉(zhuǎn)捩動量厚度雷諾數(shù)Reθt、轉(zhuǎn)捩區(qū)長度Flength、臨界動量厚度雷諾數(shù)Reθc。Reθt是湍流度Tu和壓力梯度參數(shù)λθ的函數(shù)，本文采用Menter等［2］給出的Reθt經(jīng)驗關(guān)系式。Flength和Reθc對數(shù)值計算平臺的依賴性很強，特別是計算格式，它們通過數(shù)值試驗標定獲得，下一節(jié)詳細介紹標定過程。

γ-Reθ模型和k-ω SST湍流模型的結(jié)合，是通過有效間隙因子對湍動能k方程生成項和耗散項的作用來實現(xiàn)，轉(zhuǎn)捩模型效果最終由渦粘系數(shù)來實現(xiàn)。

計算邊界條件為，物面:γ和珘Reθt的法向通量為零;自由流入口:γ=1，珘Reθt通過Reθt經(jīng)驗公式計算，取λθ=0;出口外插。

2 經(jīng)驗關(guān)系式的標定

γ-Reθ模型經(jīng)驗關(guān)系式標定是依靠數(shù)值計算和風(fēng)洞試驗結(jié)果的比對來進行的。Menter等建立γ-Reθ模型時的應(yīng)用對象主要是低速流動，例如渦輪葉片、機翼等，模型經(jīng)驗關(guān)系式標定算例是T3系列不可壓低速平板試驗，來流湍流度涵蓋了自然轉(zhuǎn)捩和Bypass轉(zhuǎn)捩。本文將γ-Reθ轉(zhuǎn)捩模型應(yīng)用到Chant-2.0軟件中的目的是實現(xiàn)高超聲速邊界層轉(zhuǎn)捩的數(shù)值模擬，模型標定理應(yīng)選用高超風(fēng)洞試驗結(jié)果，但由于高超聲速靜音風(fēng)洞的試驗數(shù)據(jù)比較少，尤其缺乏包含馬赫數(shù)、湍流度等系列變化的試驗結(jié)果，所以直接通過高超風(fēng)洞試驗數(shù)據(jù)進行模型標定是不現(xiàn)實的。因此，本文首先以低速平板試驗為參考標定出Reθc和Flength關(guān)系式，然后對轉(zhuǎn)捩模型進行高馬赫數(shù)修正，最終建立高超聲速邊界層轉(zhuǎn)捩模型。本節(jié)首先介紹低速試驗的標定過程，參考Menter等提供的平板試驗數(shù)據(jù)，試驗條件見表1，S-K和T3A-試驗為低湍流度自然轉(zhuǎn)捩，T3A和T3B為高湍流度Bypass轉(zhuǎn)捩。

表1 平板轉(zhuǎn)捩試驗的入口條件Table 1Inlet condition for flat plate test case

計算網(wǎng)格見圖1，來流入口邊界距離平板前緣0.3m，法向遠場邊界距離平板0.3m，網(wǎng)格規(guī)模為291× 121(流向×法向)，平板上分布251個點，流向最小間距Δxmin=1.0×10-3m，法向最小間距Δymin=1.0×10-5m，網(wǎng)格y+min＜0.1。

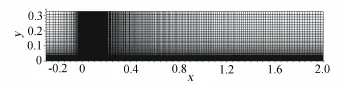
圖1 平板計算網(wǎng)格Fig.1Computational grid for flat plate

來流湍流度會隨流動而衰減，渦粘性比(μt/μ)∞越小湍流度衰減越快，為保證平板前緣處的湍流度(表1)，按照Langtry給出的自由流湍流衰減率計算入口處的湍流度，見下式:

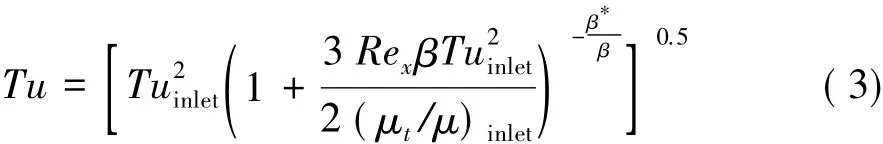
Reθc和Flength是通過數(shù)值試驗得到的，其形式并不唯一，不同學(xué)者出發(fā)點不同所采用的函數(shù)變量和系數(shù)也不相同，比如，Langtry等［2］采用的Reθc為:

本文采用Langtry等的多項式函數(shù)形式，認為Reθc和Flength僅是珘Reθt的函數(shù)，標定過程如下:1)將Reθc和Flength作為常數(shù)，指定一系列的數(shù)值對4個平板算例進行初步試算，觀察計算結(jié)果的變化規(guī)律，當計算摩阻和試驗值匹配較好時確定轉(zhuǎn)捩位置處珘Reθt的值，對應(yīng)的Reθc和Flength就作為這個珘Reθt的函數(shù)值，見表2; 2)以珘Reθt為自變量，將4個平板算例最優(yōu)的Reθc和Flength值擬合成多項式，建立Reθc(珘Reθt)和Flength(珘Reθt)的函數(shù)關(guān)系式;3)將函數(shù)關(guān)系式代入模型中進行測試，適當調(diào)整系數(shù)使得4個平板算例都能給出較好的計算結(jié)果。最后標定出的關(guān)系式見曲線圖2。

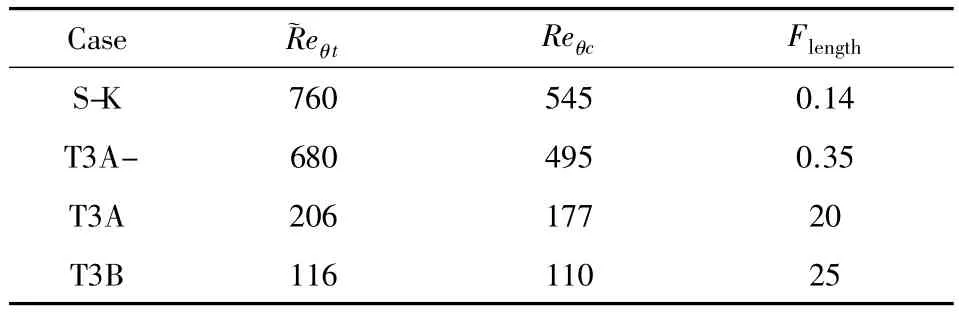
表2Reθc和Flength的數(shù)值試驗優(yōu)化參數(shù)Table 2Numerical test results for Reθcand Flength

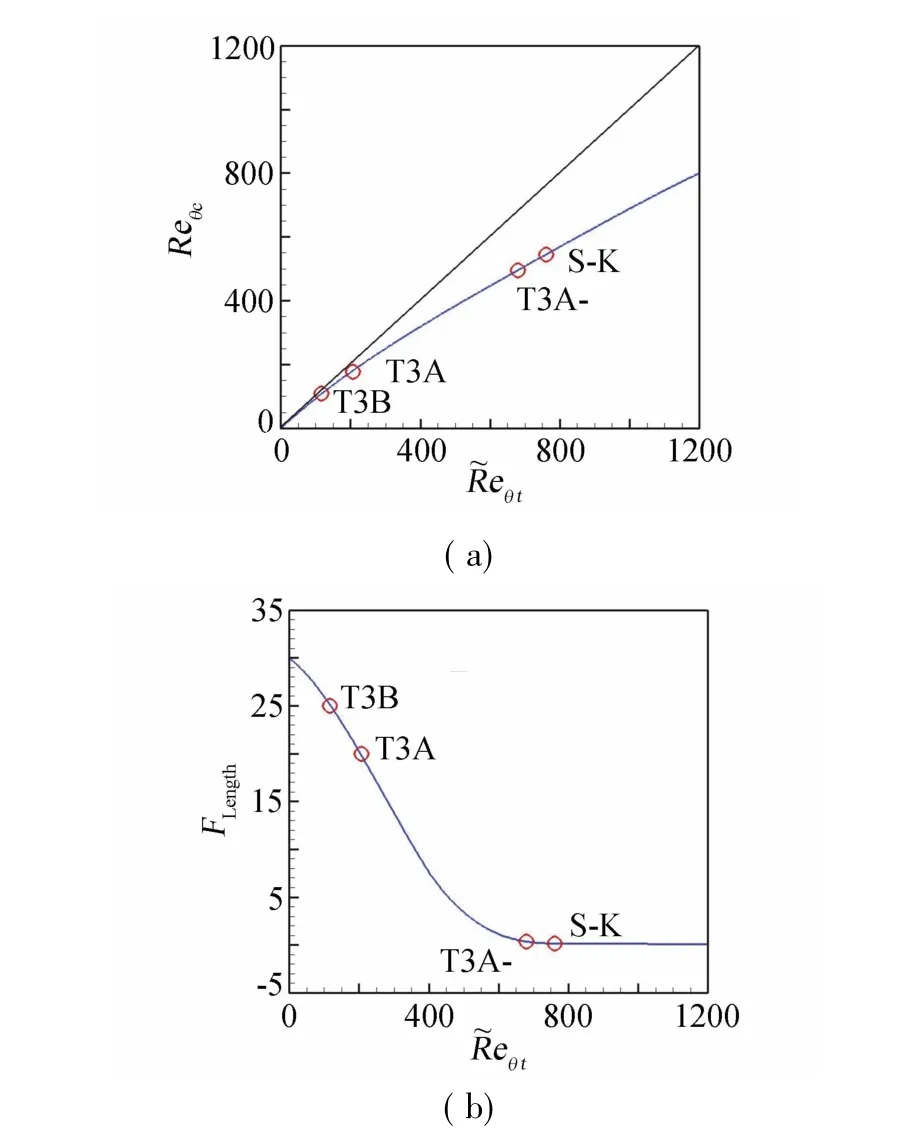
圖2擬合后的Reθc～珟Reθt、Flength～珟Reθt函數(shù)曲線圖Fig.2Reθc～珟Reθt，F(xiàn)length～珟Reθtfunction curve

圖3 為S-K算例邊界層中轉(zhuǎn)捩起點動量厚度雷諾數(shù)珘Reθt和間歇因子γ的分布圖。可以看到，珘Reθt從自由流中逐漸擴散到邊界層中，并且沿流向逐漸減小，間歇因子γ在邊界層中逐漸增長直到轉(zhuǎn)捩，γ值的分布圖與張玉倫等［9］低速軟件平臺Trip的計算結(jié)果相類似。

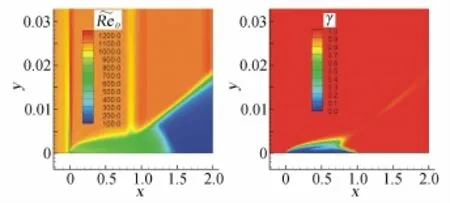
圖3S-K算例的珟Reθt和γ的分布圖Fig.3珟Reθtand γ distribution for S-K case

經(jīng)驗關(guān)系式標定后的平板計算結(jié)果見圖4，摩阻與風(fēng)洞試驗值和Menter的計算結(jié)果進行了比較，同時給出了全層流和全湍流的計算值。本文計算的轉(zhuǎn)捩起點位置和轉(zhuǎn)捩區(qū)長度都與試驗結(jié)果吻合得很好，說明經(jīng)驗關(guān)系式的標定很成功。T3B算例轉(zhuǎn)捩前摩阻比試驗值高，這可能和來流渦粘性較高有關(guān)。

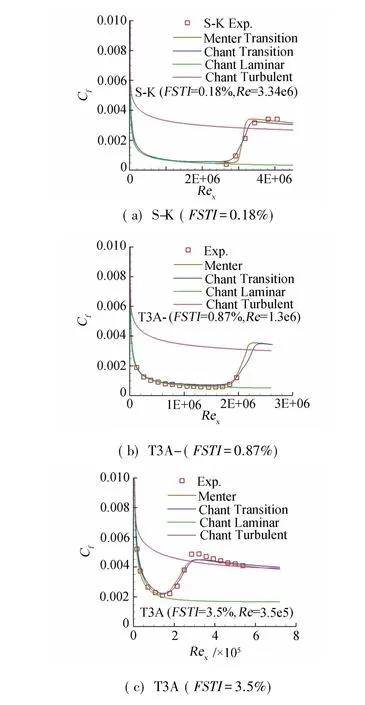
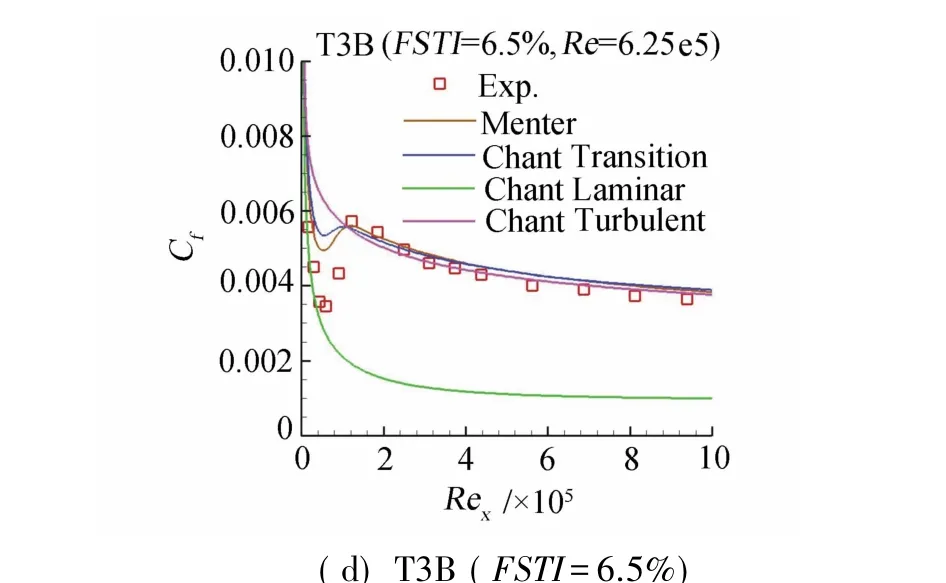
圖4 平板摩阻分布的比較Fig.4Distribution of skin friction coefficient

3 高馬赫數(shù)修正

高超聲速流動和低速流動相比，一個顯著特征是流動馬赫數(shù)很高，由此帶來高超聲速流動所特有的激波、熵層、邊界層增厚等一系列物理問題，其中由于邊界層變化帶來的粘性干擾對壓力梯度的影響較大，而邊界層轉(zhuǎn)捩對壓梯度十分敏感，逆壓梯度促發(fā)轉(zhuǎn)捩，順壓梯度延緩轉(zhuǎn)捩。

前面進行的經(jīng)驗關(guān)系式標定是基于低速風(fēng)洞試驗數(shù)據(jù)，如果直接用于高超流動轉(zhuǎn)捩模擬是不合適的，比如，轉(zhuǎn)捩模型中的Reθt經(jīng)驗關(guān)系式包含了壓力梯度的信息，在高馬赫數(shù)條件下壓力梯度參數(shù)λθ會受到馬赫數(shù)的影響，因此γ-Reθ模型在用于高超轉(zhuǎn)捩模擬中應(yīng)該適當考慮高馬赫數(shù)效應(yīng)。Gray等［11］在高超轉(zhuǎn)捩計算中對壓力梯度函數(shù)F(λθ)進行了馬赫數(shù)修正，計算表明馬赫數(shù)修正對高超尖錐轉(zhuǎn)捩位置的正確預(yù)測很關(guān)鍵。我們根據(jù)可壓縮流動邊界層理論，分析了壓力梯度參數(shù)λθ與速度梯度、動量厚度以及馬赫數(shù)的關(guān)系，近似得到了與Gray類似的壓力梯度參數(shù)的馬赫數(shù)修正:

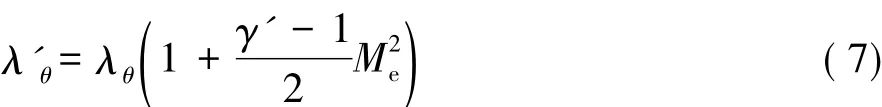
其中:γ＇為比熱比，Me為邊界層外緣馬赫數(shù)，實際使用中Me取M∞，該方法在下面計算中進行了初步檢驗。

4 算例驗證

算例一為文獻［15］中的高超平板流動，來流馬赫數(shù)M∞=4.5，來流雷諾數(shù)Re∞=6.433×106/m，來流溫度T∞=61.1K，來流湍流度0.1%。計算網(wǎng)格221× 201，壁面上分布200個點，絕熱壁條件。圖5為壓力梯度參數(shù)馬赫數(shù)修正后的γ和μt分布，與低速平板的分布相似。圖6給出了馬赫數(shù)修正前、后的摩阻分布，并與文獻中k-ω-γ轉(zhuǎn)捩模型和DNS結(jié)果［15］進行了比較。馬赫數(shù)修正前預(yù)測的轉(zhuǎn)捩位置比較靠后，與k-ω-γ和DNS的結(jié)果相差很大，修正后轉(zhuǎn)捩位置前移，轉(zhuǎn)捩起始位置接近于DNS的結(jié)果，但轉(zhuǎn)捩后的摩阻與參考值相比偏小，轉(zhuǎn)捩區(qū)略長。

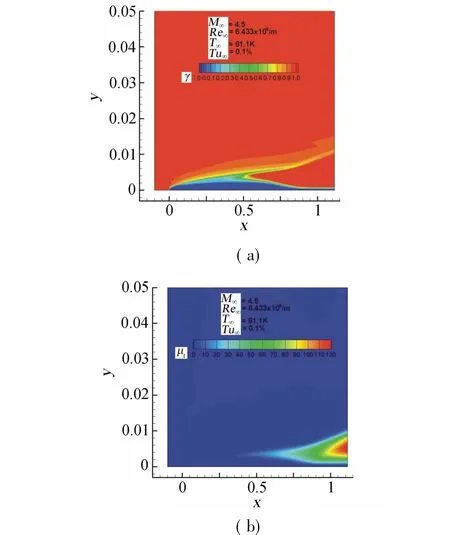
圖5 高超聲速平板γ和μt的分布Fig.5γ and μtdistribution for hypersonic flate plate

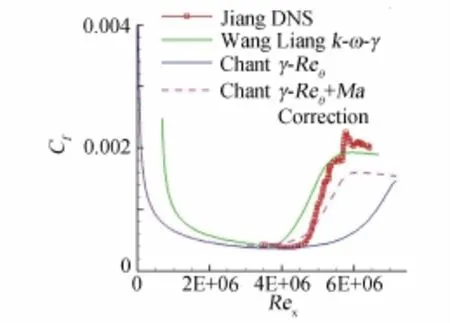
圖6 高超聲速平板摩阻分布Fig.6Skin friction distribution for hypersonic flate plate

算例二為Kimmel在AEDC B常規(guī)風(fēng)洞中進行的高超尖錐轉(zhuǎn)捩實驗［16］，模型為半錐角7°的尖頭直錐(straight cone，名義壓力梯度DPDX=0)和裙錐(flared cone，DPDX=4)，來流馬赫數(shù)M∞=7.93，來流雷諾數(shù)Re∞=6.6×106/m，來流溫度T∞=53.18K，壁面溫度Twall=303.24K，來流湍流度取Tu∞=1%，攻角0°。計算網(wǎng)格:145×201×31。圖7和圖8分別為直錐和裙錐的壁面壓力和熱流分布。裙錐在x＞0.5以后出現(xiàn)較大逆壓梯度。通過與實驗［16］、計算［11-12］的St數(shù)比較，可以看到，馬赫數(shù)修正前直錐和裙錐的模擬都沒有出現(xiàn)轉(zhuǎn)捩，修正后才能模擬出轉(zhuǎn)捩過程，轉(zhuǎn)捩起始位置和轉(zhuǎn)捩區(qū)大小與實驗比較接近。

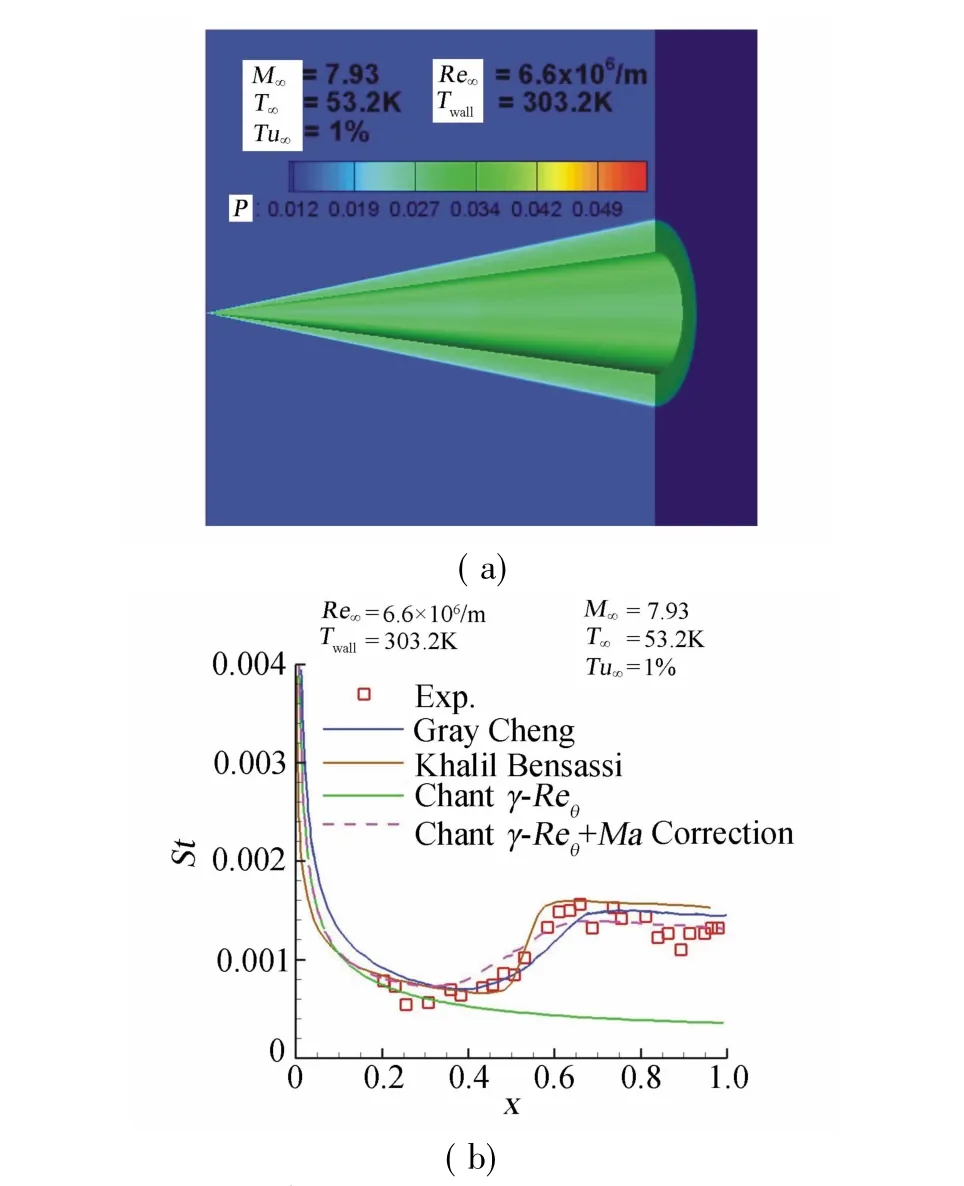
圖7 高超聲速直錐壁面壓力和熱流分布Fig.7Pressure and heat transfer distribution for hypersonic straight cone(DPDX=0)

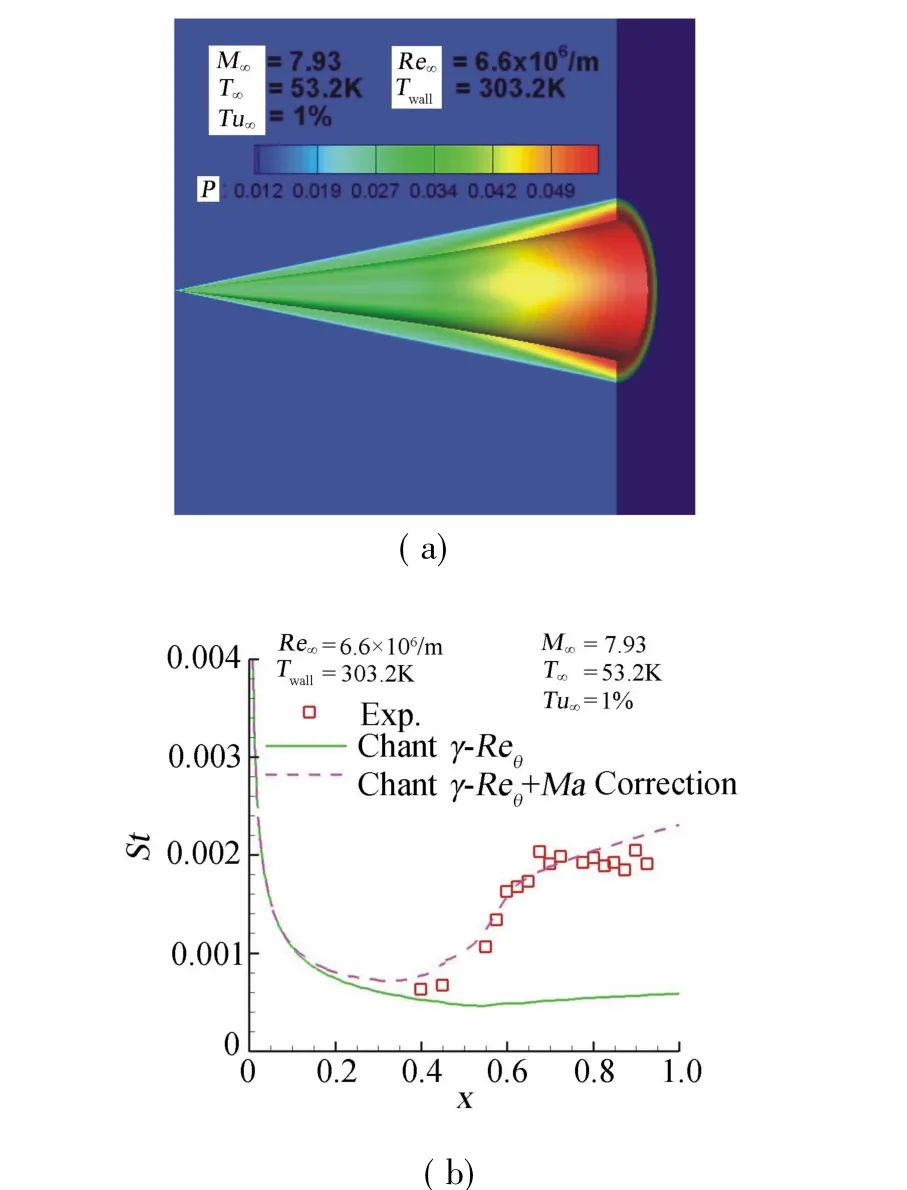
圖8 高超聲速裙錐壁面壓力和熱流分布Fig.8Pressure and heat transfer distribution for hypersonic flare cone(DPDX=4)

5 結(jié)論

通過不同來流條件下低速平板算例的大量數(shù)值試驗，我們以高超聲速數(shù)值模擬軟件平臺Chant-2.0為基礎(chǔ)，對γ-Reθ轉(zhuǎn)捩模型的經(jīng)驗關(guān)系式Reθc和Flength進行了成功的標定，取得了與試驗數(shù)據(jù)符合較好的計算結(jié)果，并且針對高超聲速轉(zhuǎn)捩問題，對原有模型進行了高馬赫數(shù)修正，在M∞=4.5平板和M∞=7.93的尖錐上進行了初步驗證，較好地模擬了轉(zhuǎn)捩位置，說明修正后的γ-Reθ模型具有模擬高超聲速轉(zhuǎn)捩的能力，值得進一步深入研究。下一步，我們將在三維高超流動轉(zhuǎn)捩上繼續(xù)開展轉(zhuǎn)捩模型的修正研究，希望能夠使γ-Reθ模型在復(fù)雜高超聲速轉(zhuǎn)捩模擬中具有工程實用價值。

［1］Menter F R，Langtry R B，Likki S R，et al.A correlation-based transition model using local variables—part I:model formulation［J］.Journal of Turbomachinery，2006，128:413-422.

［2］Langtry R B，Menter F R.Correlation-based transition modeling for unstructured parallelized computational fluid dynamic codes［J］.AIAA Journal，2009，47(12):2894-2906.

［3］Langtry R B，Menter F R.Transition modeling for general CFD application in aeronautics［R］.AIAA 2005-522.

［4］Langtry R B，Menter F R，Volker S.Transition modeling for general purpose CFD codes［J］.Flow Turbulence Combust，2006，77:277-303.

［5］Atsushi Toyoda，Takashi Misaka，Shigeru Obayashi.An application of local correlation-based transition model to JAXA high-lift configuration model［R］.AIAA 2007-4286.

［6］Niels N Srensen.CFD modeling of laminar-turbulent transition for airfoils and rotors using the γ-Reθmodel［R］.AIAA 2008-7323.

［7］Keerati Suluksna，Pramote Dechaumphai，Ekachai Juntasaro.Correlations for modeling transitional boundary layers under influences of freestream turbulence and pressure gradient［J］.International Journal of Heat and Fluid Flow，2009，30:66-75.

［8］Martin Krause，Marek Behr，Josef Ballmann.Modeling of transition effects in hypersonic intake flows using a correlation-based intermittency model［R］.AIAA 2008-2598.

［9］張玉倫，王光學(xué)，孟德虹，等.γ-Reθ轉(zhuǎn)捩模型的標定研究［J］，空氣動力學(xué)學(xué)報，2011，29(3):295-301.

［10］牟斌，江雄，肖中云，等.γ-Reθ轉(zhuǎn)捩模型的標定與應(yīng)用［J］.空氣動力學(xué)學(xué)報，2012，31(1):103-109.

［11］Gary Cheng，Robert Nichols，Kshitij D Neroorkar，et al.Validation and assessment of turbulence transition models［R］.AIAA 2009-1141.

［12］Khalil Bensassi，Andrea Lani，Patrick Rambaud.Numerical investigations of local correlation-based transition model in hypersonic flows［R］.AIAA 2012-3151.

［13］張曉東，高正紅.關(guān)于補充Langtry的轉(zhuǎn)捩模型經(jīng)驗修正式的數(shù)值探討［J］.應(yīng)用數(shù)學(xué)和力學(xué)，2010，31(5):544-552.

［14］顏培剛，韓萬金，嚴紅明.應(yīng)用γ-Reθ湍流模型模擬超聲速進氣道流動［J］.哈爾濱工業(yè)大學(xué)學(xué)報，2011，43(1):95-98.

［15］Wang L，Song Fu.Development of an intermittency equation for the modeling of the supersonic/hypersonic boundary layer flow transition［J］.Flow Turbulence Combust，2011，87:165-187.

Calibration of transition model for hypersonic numerical simulation platform

Zhang Yifeng1，Lei Jing2，Zhang Yirong1，Mao Meiliang1，Chen Jianqiang1
(1.Computational Aerodynamics Institute of China Aerodynamics Research and Development Center，Mianyang621000，China; 2.Beijing Institute of Nearspace Vehicle’s Systems Engineering，Beijing100076，China)

Based on CARDC hypersonic numerical simulation platform Chant-2.0，applications of γ-Reθmodel to hypersonic boundary layer transition are investigated preliminarily.The transition onset and length are predicted by solving two transport equations for turbulence intermittency factor and momentum thickness Reynolds number.Firstly，γ-Reθtransition model using local correlation functions is calibrated through four cases of low speed flat flows，and in the process freestream turbulence intensities have a wide range from low level natural transition to high level bypass transition.Then，taking account of flow properties of hypersonic boundary layer，the pressure gradient function used in the transition model's Reθtcorrelation is properly modified for high Mach number flows.Finally，by adopting the new model functions，hypersonic boundary layer transitions of flat and sharp cone are calculated and compared with referrence data.The simulation results indicate that the specially calibrated correlations for hypersonic platform software can accurately predict the onset and length of transition region in low speed cases，and high Mach number correction shows good performance in hypersonic simulations.

hypersonic flow;numerical simulation;transition model;calibration

V211.3

Adoi:10.7638/kqdlxxb-2014.0110

0258-1825(2015)01-0042-06

2014-09-18;

2014-09-30

張毅鋒(1975-)，男，副研究員，研究方向:高超聲速流動數(shù)值模擬、高精度數(shù)值方法.E-mail:zyf63867@163.com

張毅鋒，雷凈，張益榮，等.高超聲速數(shù)值模擬平臺轉(zhuǎn)捩模型的標定［J］.空氣動力學(xué)學(xué)報，2015，33(1):42-47.

10.7638/kqdlxxb-2014.0110.Zhang Y F，Lei J，Zhang Y R，et al.Calibration of transition model for hypersonic numerical simulation platform［J］.Acta Aerodynamica Sinica，2015，33(1):42-47.