基于非結(jié)構(gòu)動網(wǎng)格的非定常激波裝配法

劉君，鄒東陽，徐春光

基于非結(jié)構(gòu)動網(wǎng)格的非定常激波裝配法

劉君，鄒東陽，徐春光

(大連理工大學航空航天學院，遼寧大連116024)

從ALE方程出發(fā)，通過修正體積的新思路構(gòu)建離散幾何守恒律，基于非結(jié)構(gòu)動網(wǎng)格的信息傳遞方法得到網(wǎng)格重構(gòu)以后新網(wǎng)格的流場參數(shù)，采用一階格式捕捉法得到的流場確定裝配法的初始激波位置，成功地把激波裝配法應用到非定常流動的模擬。模擬超聲速飛行環(huán)境下整流罩分離的非定常流固耦合過程，在馬赫數(shù)6條件下裝配法和捕捉法的計算結(jié)果完全一致，隨著馬赫數(shù)增加，二階精度格式的捕捉法需要進行調(diào)整限制器參數(shù)、時間步長等人工干預，但是裝配法直到馬赫數(shù)20計算過程沒有出現(xiàn)異常。該基于非結(jié)構(gòu)動網(wǎng)格技術(shù)的激波裝配方法，與傳統(tǒng)的激波裝配方法相比，能夠用于復雜外形產(chǎn)生的非規(guī)則形狀激波和非定常流動產(chǎn)生的運動激波，解決二階精度有限體積法用于高馬赫數(shù)飛行條件下多體分離過程的流動模擬時遇到的穩(wěn)定性問題。

激波裝配;非結(jié)構(gòu)動網(wǎng)格;非定常流動;高超聲速

激波是可壓縮流體動力學中最重要的物理現(xiàn)象，模擬激波自然也構(gòu)成計算流體力學(CFD)主要的研究內(nèi)容。激波的模擬方法分為捕捉和裝配兩種。1953年，Lax提出自動捕捉雙曲型守恒率方程間斷解的一階格式，在應用中發(fā)現(xiàn)數(shù)值解存在非物理波動; 1959年，Godunov基于弱解理論，利用間斷滿足的Riemann分解的特性，構(gòu)造出物理背景清晰計算穩(wěn)定的一階格式［1］。由于這兩種格式都只有一階精度，計算得到的激波需要若干網(wǎng)格點過渡(所謂激波較寬)。直到1983年Harten提出TVD格式才實現(xiàn)二階精度，使得激波分辨率得以提高。其后發(fā)展了許多高精度格式，如NND、ENO、WENO等［2］，近幾年三階乃至更高階的WCNS也得到實際應用［3-5］。1966年，Moretti根據(jù)激波上下游流動參數(shù)滿足R-H關(guān)系式的特點提出激波裝配法［1］，高精度高效率地模擬出鈍體頭部脫體激波，二維情況下裝配法使用10×16個網(wǎng)格得到的壓力分布的精度不遜于當代捕捉法使用385×513個網(wǎng)格的精度［6］，極大地推動了當時超聲速流動的應用研究，直到上世紀80年代后期依然是主流算法［7］。然而，這種算法需要事先確定激波位置，應用受到極大限制，隨著高精度捕捉法的發(fā)展，裝配法的研究熱情逐漸消退。

激波空間尺度只有幾個分子的平均自由程［8］。在海平面標準狀況下，馬赫數(shù)M1=2.95的正激波厚度大約為6.6×10-8m，而常見的飛行器在10m量級，目前航天航空領(lǐng)域CFD應用中10-3m量級網(wǎng)格很少見，因此采用捕捉方法模擬出來的激波寬度要比實際的激波厚度大得多。激波內(nèi)部處于熱力學非平衡狀態(tài)，而建立Euler或NS方程時采取了熱力學局部平衡假設、密度不存在劇烈變化的Stokes假設以及采用了忽略松弛時間的狀態(tài)方程等，從理論角度看，從Euler或NS方程出發(fā)捕捉激波，即使未來幾十年后計算機發(fā)展使得激波厚度內(nèi)布置若干網(wǎng)格成為常態(tài)，只要過度區(qū)有1個網(wǎng)格點，也會產(chǎn)生非物理波動。描述激波最完善的數(shù)學理論是雙曲型守恒率方程的弱解理論。它把激波看作無厚度的間斷，流動參數(shù)在此發(fā)生突躍。

由于捕捉法計算激波存在諸多理論缺陷，文獻［6］中認為捕捉法經(jīng)過36年(1966-2001)的發(fā)展依然無法超越裝配法。近幾年國外一些學者重新審視裝配法，解決了高精度格式應用于高馬赫數(shù)流動時在激波附近出現(xiàn)波動的問題［9-10］。Paciorri等人采用在捕捉法得到的流場基礎(chǔ)上裝配浮動激波的新思路突

0 引言

破傳統(tǒng)裝配法的限制，極大推動了應用領(lǐng)域拓展［11-13］。浮動激波裝配法通過局部網(wǎng)格重構(gòu)來形成內(nèi)部激波邊界，由于激波運動以后需要在背景網(wǎng)格上重新定位和插值，流場信息傳遞使其難以用于非定常流動［11-13］。

本文利用文獻［14］建立在ALE(Arbitrary Lagrangian-Eulerian)方程基礎(chǔ)上的非結(jié)構(gòu)動網(wǎng)格技術(shù)發(fā)展能夠用于非定常流動的裝配法。

1ALE形式控制方程及其計算方法

采用ALE描述的三維可壓縮非定常N-S方程的積分形式:

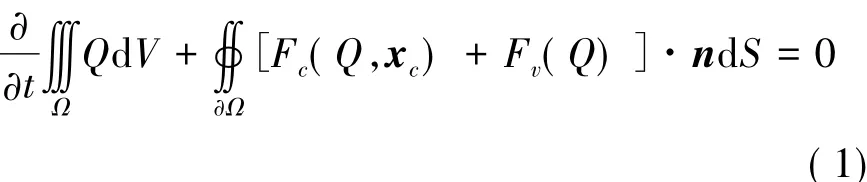
其中，Ω為控制體，Ω為控制邊界，n為控制體邊界外法向向量，dV為體積微元，dS為面積微元，xc為網(wǎng)格運動速度。

計算方法采用文獻［14］中介紹的基于混合網(wǎng)格的有限體積方法，對于守恒變量存貯在單元中心的格心格式，空間離散第i個控制體:

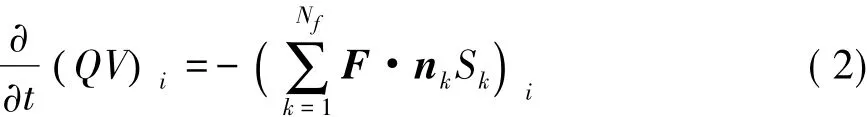
其中，F(xiàn)k、nk、Sk分別為第k個面元的通量、外法向單位矢量和面積，Nf為控制體表面?zhèn)€數(shù)。假設物理量在單元內(nèi)線性分布得到空間二階精度的有限體積法格式，第i個控制體的第k個表面中心點的變量值:

Qik=Qi+ik!Qi·rik(3)其中，!Qi是單元內(nèi)物理量梯度，采用Green公式計算梯度，rik是單元中心到表面中心的矢徑，ik是為了抑制激波附近可能出現(xiàn)的非物理振蕩而引入的限制器，本文采用Venkatakrishman限制器。兩側(cè)單元在表面k處的重建值形成物理量的間斷，將其視為近似的一維Riemann問題，可以利用Riemann問題的各種求解方法計算單元k處的無粘通量。在本文軟件中包含有Van Leer、Roe、AUSM、HLLC等多種分裂格式。時間離散采用二階時間精度的四步Runge-Kutta方法。計算中穩(wěn)定性要求時間步長滿足CFL條件:

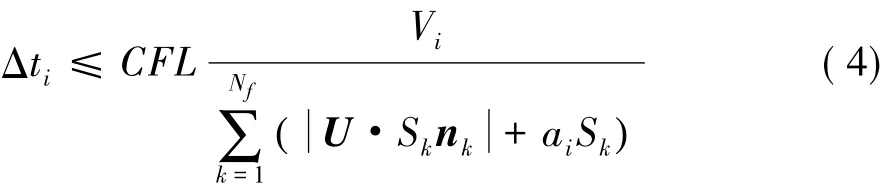
式中，U為流體速度，ai是當?shù)芈曀伲琕i是單元i的體積。對四步Runge-Kutta格式，CFL≤2槡2。全場時間步長是所有當?shù)貢r間步長的最小值，即Δt= min(Δti)。

鋼渣砂可以作為砂漿集料，選擇大粒徑鋼渣可提高砂漿的抗壓強度[28]。用鋼渣等體積替代石英砂配制干混砂漿，粒徑小于1.18 mm的鋼渣砂配制的干混砂漿可滿足力學性能和膨脹性能的要求[29]。在鋼渣摻量較小時，用鋼渣代砂制備砂漿后對其干縮性能和抗凍性能進行試驗研究表明，鋼渣砂漿與普通砂漿的自然養(yǎng)護干燥收縮值比較接近[30]。

計算時還需要考慮離散幾何守恒律(Discrete Geometric Conservation Law—DGCL);很多時候網(wǎng)格變形算法需要結(jié)合網(wǎng)格重構(gòu)實現(xiàn)大變形或大位移，這又涉及到新舊網(wǎng)格之間的信息傳遞。

1.1 離散幾何守恒律

對于均勻流場，NS方程的質(zhì)量方程:在離散空間，從n推進到n+1時刻，微元體積從Vn變化為Vn+1，對于顯式算法，第i個面Sni以速度xci運動形成的體積增量記為ΔVni=xci·niSni，對于全隱算法，第i個以速度xci運動形成的體積增量記為ΔVni+1=xci·niSni+1，顯然有:

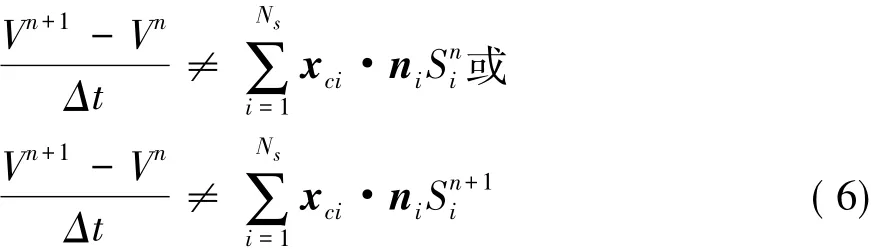
其中，Ns表示單元所含面元個數(shù)。這種幾何計算誤差必然影響流場計算，因此需要構(gòu)建DGCL來消除。

根據(jù)所修正的參數(shù)把國內(nèi)外文獻構(gòu)造的DGCL分為三類算法:第一類修正網(wǎng)格面積，采用平均面積:1，這種算法最早和幾何守恒律概念［15］一起提出，難以應用于涉及2個以上時間層的高階隱格式;第二類修正網(wǎng)格運動速度，如果時間二階格式離散左端項:

采用如下速度ugi來代替實際的網(wǎng)格運動速度xci計算［16］:

這種算法進行流固耦合模擬時，流體界面不能按照給定速度運動，無法滿足速度相等條件;第三類同時修改網(wǎng)格面積和網(wǎng)格速度［17-18］，部分改進了以上不足。

既保證流固界面速度，也不受空間離散格式限制，完全解決了DGCL問題，文獻［20-21］中給出驗證算例，效果很好。

1.2 信息傳遞

網(wǎng)格重構(gòu)以后，采用插值傳遞新舊網(wǎng)格之間流場信息，線形插值導致激波分辨率降低，ENO插值引起非物理波動，很難構(gòu)造適合激波的3階插值。為了避免新舊網(wǎng)格之間流場信息傳遞過程產(chǎn)生新誤差，文獻［22］提出一種基于動網(wǎng)格的信息傳遞方法，下面以二維問題為例對其基本原理進行介紹。

問題如圖1(a)所示，已知n時刻舊網(wǎng)格中O點的流場參數(shù)，需要得到n+1時刻新網(wǎng)格的P點和Q點流場參數(shù)。如圖1(b)所示，在舊網(wǎng)格的基礎(chǔ)上時間方向推進Δt，計算得到n+1時刻流場參數(shù)的同時，采用動網(wǎng)格技術(shù)保持O點及周圍所涉及的網(wǎng)格不變形但是同一速度運動，使得O點平移到P點;同樣，在舊網(wǎng)格基礎(chǔ)上時間方向推進Δt，將O點平移到Q點。由于P和Q所在的空間位置正好是新網(wǎng)格的點，如圖1(c)所示，因此通過動網(wǎng)格技術(shù)得到n+1時刻的流場參數(shù)，在此基礎(chǔ)上放棄舊網(wǎng)格，采用新網(wǎng)格繼續(xù)計算。可以證明，對于以上時間空間二階精度的有限體積法格式，這種方法不引入誤差，因此稱為高精度信息傳遞算法［14］。時間顯式格式的穩(wěn)定性限制網(wǎng)格運動速度，在多維條件下少量網(wǎng)格需要多步時間推進才能實現(xiàn)統(tǒng)一時間Δt流場，為此文獻［21］提出了一些改進措施。

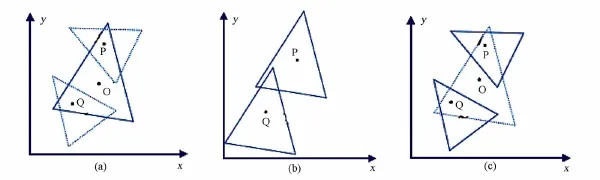
圖1 信息傳遞原理圖Fig.1Schematic of information transfer

1.3 非結(jié)構(gòu)動網(wǎng)格技術(shù)

1990年Batina首次將彈簧比擬法用于三角形網(wǎng)格的變形［23］。它的原理是將連接網(wǎng)格邊視為彈簧，整個計算區(qū)域網(wǎng)格構(gòu)成彈簧系統(tǒng)，在彈簧系統(tǒng)內(nèi)部節(jié)點(網(wǎng)格點)列出力的平衡方程組，邊界發(fā)生運動或變形后使彈簧網(wǎng)絡受到拉伸和擠壓，整個彈簧系統(tǒng)受力發(fā)生變化，通過求解彈簧網(wǎng)絡的平衡方程來更新網(wǎng)格節(jié)點的位置。這種方法只考慮了彈簧拉壓，扭轉(zhuǎn)變形易出現(xiàn)網(wǎng)格折穿(snap-through)。1998年Farhat等人在二維網(wǎng)格頂點處施加扭轉(zhuǎn)彈簧增加抗扭轉(zhuǎn)能力取得實效，但在推廣到三維網(wǎng)格遇到困難［24-25］。2000年Blom等人根據(jù)三角形單元邊對應的頂角來修正線彈簧剛度系數(shù)，提出半扭轉(zhuǎn)彈簧方法［26］，2003年郭正和劉君針對四面體，采用不包含該邊的二面角作為頂角，把這種方法推廣到了三維情形，同時通過求解固體導熱方程得到的內(nèi)部節(jié)點溫度作為參數(shù)來增加動邊界附近網(wǎng)格層的彈簧剛度系數(shù)，提高了網(wǎng)格變形能力［27］。本文采用［27］發(fā)展的彈簧比擬法，所求解的力平衡方程組對角占優(yōu)，采用Jacobia迭代能較快收斂。

2 基于非結(jié)構(gòu)動網(wǎng)格的激波裝配法

半圓柱前形成脫體激波結(jié)構(gòu)的無粘流場，計算網(wǎng)格如圖2所示。為了加快收斂速度和提高非定常流場計算的初值精度，本文借鑒文獻［11-13］的新思路，在捕捉法流場基礎(chǔ)上按照如下算法確定裝配法的初始激波位置:(1)尋找全場密度梯度最大單元，記為E0，然后找出該單元頂點周圍密度梯度最大的單元，記為E1;(2)增加排除標記過的單元、到Ei-1格心大于Ei與Ei-1格心距離約束，找出與Ei單元共點的

密度梯度最大的單元，記為Ei+1，直到邊界;(3)采用Bézier方法進行擬合單元格心坐標，得到的初始激波位置如圖2中曲線所示，用作裝配法生成網(wǎng)格的邊界。

對于裝配法重新生成的新網(wǎng)格，除了激波邊界網(wǎng)格外，按照上面介紹的信息傳遞方法給出流動參數(shù)。對于激波邊界處新網(wǎng)格的流場參數(shù)，先在舊網(wǎng)格中定位，然后取舊網(wǎng)格中對應單元的相鄰單元中最大壓力作為激波后壓力p2，結(jié)合激波前壓力p1可以計算激波在靜止環(huán)境中的運動速度:

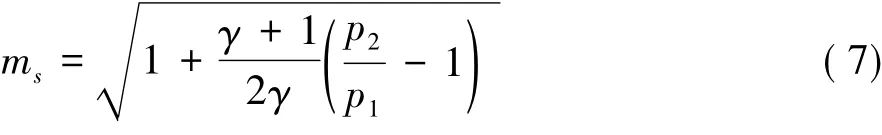
在均勻來流速度為v1的風軸系下，激波相對運動速度:

其中，vn1=μ·v1·n，μ=sign v1·n ()。

本文采用基于非結(jié)構(gòu)動網(wǎng)格的激波裝配法，不需要像文獻［11-13］那樣處理浮動激波，網(wǎng)格按照以上激波速度進行運動，即xc=vs。為使激波邊界新網(wǎng)格的流場參數(shù)相容，引入相對激波馬赫數(shù)M1=vn1+xc· n，根據(jù)R-H關(guān)系式確定波后密度和速度:

圖2 計算網(wǎng)格Fig.2Computational grids

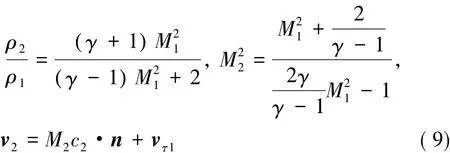
其中vτ1為均勻來流在界面上切向分量。

按照以上捕捉法方法編制程序模擬馬赫數(shù)大于6的鈍體無粘繞流場。如果初場取自由來流參數(shù)，先用一階迎風格式得到收斂流場，然后用二階精度格式進一步提高分辨率。對于如圖2所示較稀疏的計算網(wǎng)格，隨著馬赫數(shù)增大激波增強，采用二階格式后需要探索調(diào)整限制器參數(shù)、計算時間步長等才能避免發(fā)散或振蕩，到了馬赫數(shù)20時，采用Roe、AUSM、HLLC等空間格式很難收斂到穩(wěn)定解，基于非結(jié)構(gòu)動網(wǎng)格的激波裝配法沒有出現(xiàn)不收斂現(xiàn)象。圖3為馬赫數(shù)等于20時采用二階Vanleer分裂格式捕捉和裝配得到的馬赫數(shù)等值線圖的比較。物面壓力和Lyubimov的經(jīng)典文獻［28］、文獻［7］進行比較，符合很好，由于篇幅有限，這里不再贅述。

本文采用基于非結(jié)構(gòu)動網(wǎng)格的激波裝配法成功地計算出超高馬赫數(shù)下的定常流場。下面對如圖4所示的整流罩分離動態(tài)過程進行模擬。整流罩初始開啟角度為5°，在氣動力作用下整流罩繞法蘭旋轉(zhuǎn)動現(xiàn)象。在計算過程兩種方法均需要多次網(wǎng)格重構(gòu)，重構(gòu)生成新網(wǎng)格在激波后區(qū)域尺度接近和數(shù)目相當，采用前面介紹的新舊網(wǎng)格之間信息傳遞方法給出新網(wǎng)格上參數(shù)。文獻［14］提供了采用捕捉法模擬超聲速多體分離干擾流場的大量驗證算例，本文以捕捉法的結(jié)果作為考核標準，模擬飛行馬赫數(shù)6條件下整流罩動態(tài)分離過程。對比整流罩分離過程中捕捉法和裝配法得到的不同時刻的馬赫云圖，如圖5所示，以及質(zhì)心和姿態(tài)角隨時間變化曲線，如圖6、7所示。可以看出，采用裝配法得到的流場結(jié)構(gòu)、氣動力驅(qū)動運動特性與捕捉法符合較好。對比表明本文采用的基于非結(jié)構(gòu)動網(wǎng)格的激波裝配法可以很好地模擬非定常激波。

比較了捕捉法一階迎風和二階格式的收斂解得到的初始激波位置，幾乎沒有區(qū)別，這一現(xiàn)象定性合理，因為不同精度格式對于已經(jīng)分辨出來的激波主要差異在于寬度(網(wǎng)格點數(shù))，最大梯度的位置差異較小。如果格式在激波區(qū)光滑過渡，盡管寬度不同，但是若干網(wǎng)點后必然恢復到激波后參數(shù)，基于這樣的認識，提出采用舊網(wǎng)格的相鄰網(wǎng)格單元中最大壓力作為激波邊界網(wǎng)格壓力的計算方法來消除不同精度格式對初場的影響。通過圖6和圖7的對比發(fā)現(xiàn)，采用兩種方法得到的計算結(jié)果基本一致。由于激波裝配法無法消除捕捉法提供初場帶來的誤差，可以得出結(jié)論:采用激波裝配方法的計算過程沒有引入新的誤差。

隨著馬赫數(shù)增加，二階格式的捕捉法難以正常運行，需要不斷在計算發(fā)散以后進行人工干預，基于一階迎風格式捕捉到激波位置作為初始邊界的裝配法計算沒有任何問題，圖8給出馬赫數(shù)20時分離過程中不同時刻的壓力云圖。打開，達到30°時整流罩分離進行六自由度自由運動。該流場存在激波、膨脹波等諸多復雜的非定常流

圖3 馬赫數(shù)等值線圖Fig.3Mach iso-contours

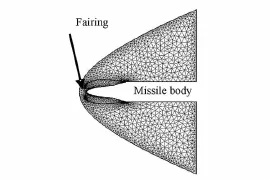
圖4 激波裝配計算初始網(wǎng)格Fig.4Initial computational grids for shock-fitting

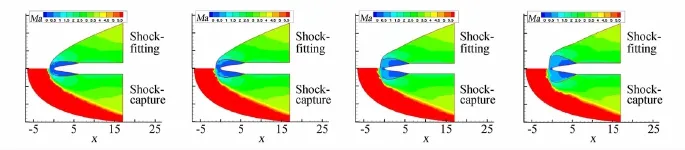
圖5Ma=6整流罩分離過程中不同時刻馬赫云圖Fig.5Mach contours change versus time in the process of fairing separation at Ma=6

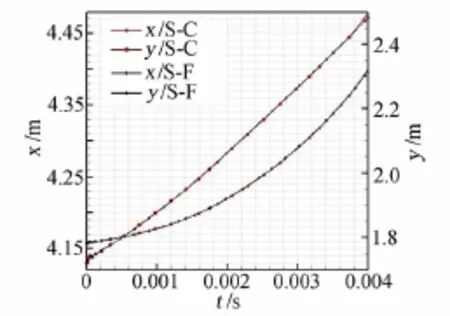
圖6 整流罩質(zhì)心運動(S-C:捕捉法;S-F:裝配法)Fig.6Fairing's barycenter movement versus time (S-C:shock-capturing;S-F:shock-fitting)

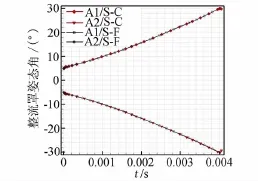
圖7 整流罩姿態(tài)角變化(A1:上片角度;A2:下片角度)Fig.7Fairing'angle of pitch change versus time (A1:angular of upper panel A2:angular of lower panel)

圖8Ma=20整流罩分離過程中不同時刻壓力云圖Fig.8Pressure contours change versus time in the process of fairing separation at Ma=20

3 結(jié)論

本文提出了以一種新的基于非結(jié)構(gòu)動網(wǎng)格技術(shù)的激波裝配方法，采用一階格式捕捉法得到的流場確定裝配法所需的初始激波位置，將激波裝配法成功地應用到非定常流動產(chǎn)生的運動激波的模擬，復雜外形產(chǎn)生的非規(guī)則形狀激波的模擬，解決了高精度格式捕捉強激波遇到的穩(wěn)定性問題。

［1］Li S B.Theory of dissipative conservation scheme［M］.Beijing: Higher Education Press，1997.(in Chinese)李松波.耗散守恒格式理論［M］.北京:高等教育出版社，1997.

［2］Zhang H X，Shen M Y.Computational fluid dynamics-theory and application of difference scheme［M］.Beijing:National Defense Industry Press，2003.(in Chinese)張涵信，沈孟育.計算流體力學—差分格式原理和應用［M］.北京:國防工業(yè)出版社，2003.

［3］DENG X G，ZHANG H X.Developing high-order weighted compact nonlinear schemes［J］.Journal of Computational Physics，2000，165(1):22-24.

［4］Li Q，Sun D，Zheng Y K，Zhang H X.On a class of center-typed third order difference scheme orienting to engineering utilizations［J］.Acta Aerodynamics Sinica，2013，31(4):466-493.(in Chinese)李沁，孫東，鄭永康，張涵信.一類中心型三階格式及其應用［J］.空氣動力學學報，2013，31(4):466-493.

［5］Zhang S H，Li H，Liu X L.A direct numerical simulation of the complex multi-scale flow with shock，vortex and sound wave［J］.Computer Engineering＆Science，2012，34(8):99-107.(in Chinese)張樹海，李虎，劉旭亮.含激波、旋渦和聲波的復雜多尺度流動的直接數(shù)值模擬［J］.計算機工程與科學，2012，34(8):99-107.

［6］Moretti G.Thirty-six years of shock fitting［J］.Computers＆Fluids，2002，31:719-723.

［7］Ye Y D.Numerical simulation of the modified space shuttle orbiterinviscid flowfield［D］.Changsha:National University of Defence Technology，1991.(in Chinese)葉友達.航天飛機簡化外形無粘流場的數(shù)值模擬［D］.長沙:國防科技大學，1991.

［8］Tong B G，Kong X Y，Deng G H.The gas dynamics［M］.Beijing: Higher Education Press，2012.(in Chinese)童秉綱，孔祥言，鄧國華.氣體動力學［M］.北京:高等教育出版社，2012.

［9］Prakash A，Parsons N，Wang X，Zhong X.High-order shock-fitting methods for direct numerical simulation of hypersonic flow with chemical and thermal nonequilibrium［J］.Journal of Computational Physics，2011，230:8474-8507.

［10］Najafi M，Hejranfar K，Esfahanian V.Application of a shock-fitted spectral collocation method for computing transient high-speed inviscid flows over a blunt nose［J］.Journal of Computational Physics，2014，257:954-980.

［11］Paciorri R，Bonfiglioli A.A shock-fitting technique for 2D unstructured grids［J］.Computers＆Fluids，2009，38:715-726.

［12］Paciorri R，Bonfiglioli A.Shock interaction computations on unstructured，two-dimensional grids using a shock-fitting technique［J］.Journal of Computational Physics，2011，230:3155-3177.

［13］Bonfiglioli A，Grottadaurea M，Paciorri R，Sabetta F.An unstructured，three-dimensional，shock-fitting solver for hypersonic flows［J］.Computers＆Fluids，2013，73:162-174.

［14］Liu J，Bai X Z，Guo Z.The computational method of unstructured moving grids［M］.Changsha:National University of Defence Technology Press，2009.(in Chinese)劉君，白曉征，郭正.非結(jié)構(gòu)動網(wǎng)格計算方法［M］.長沙:國防科技大學出版社，2009.

［15］Thomas P D，Lombard C K.The geometric conservation law-a link beween finite-difference and finite-volume methods of flow computation on moving grids［R］.AIAA 1978-1208.

［16］Mavriplis D J，Yang Z.Construction of the discrete geometric conservationa law for high-order time-accurate simulations on dynamic meshes［J］.Journal of Computational Physics，2006，213:557-573.

［17］Farhat C，Geuzaine P.Design and analysis of robust ALE time-integrators for the solution of unsteady flow problems on moving grids［J］.Computer Methods in Applied Mechanics and Engineering，2004，193:4073-4095.

［18］Zhang L P，Wang Z J.A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes［J］.Computers＆Fluids，2004，33:891-916.

［19］Liu J，Bai X Z，Zhang H X，Guo Z.Discussion about GCL for diforming grids［J］.Aeronautical Computing Technique，2009，39 (4):1-5.(in Chinese)劉君，白曉征，張涵信，郭正.關(guān)于變形網(wǎng)格“幾何守恒律”概念的討論［J］.航空計算技術(shù)，2009，39(4):1-5.

［20］Liu J，Xu C G，Liu Y.New scheme for interface boundary of fluid/ structure interaction problems［C］//2012 National conference of CFD，2012:247-253.(in Chinese).劉君，徐春光，劉瑜.數(shù)值模擬流固耦合的界面新算法［C］//2012全國計算流體力學會，2012:247-253.

［21］Xu C G.Research on numerical simulation and application of complicated jet flow field［D］.Changsha:National University of Defence Technology，2002.(in Chinese)徐春光.復雜噴流流場數(shù)值模擬及應用研究［D］.長沙:國防科技大學，2002.

［22］Liu J，Bai X Z，Guo Z，et al.A new method for transferring flow information among meshes［J］.Computational Fluid Dynamics Journal，2007，15(4):509-514.

［23］Batina J T.Unsteady Euler airfoil solutions using unstructured dynamic meshes［J］.AIAA Journal，1990，28(8):1381-1388.

［24］Farhat C，Degand C，Koobus B，et al.Torsional springs for two-dimensional dynamic unstructured fluid meshes［J］.Computer Methods in Applied Mechanics and Engineering，1998，163:231-245.

［25］Degand C，F(xiàn)arhat C.A three-dimensional torsional spring analogy method for unstructured dynamic meshes［J］.Computers＆Structures，2002，80:305-316.

［26］Blom F J.Considerations on the spring analogy［J］.International Journal for Numerical Methods in Fluids，2000，32:647-668.

［27］Guo Z，Liu J，Qu Z H.Dynamic unstructured grid method with applications to 3D unsteady flows involving moving boundaries［J］.Acta Mechanics Sinica，2003，35(2):140-146.(in Chinese)郭正，劉君，瞿章華.非結(jié)構(gòu)動網(wǎng)格在三維可動邊界問題中的應用［J］.力學學報，2003，35(2):140-146.

［28］Lyubimov A N，Rusanov V V.Gas flows past blunt bodies，PART II:Tables of the gas dynamic functions［R］.NASA TT-F-715，197.

An unsteady shock-fitting technique based on unstructured moving grids

Liu Jun，Zou Dongyang，Xu Chunguang
(School of Aeronautics and Astronautics，Dalian University of Technology，Dalian116024，China)

A shock-fitting technique based on unstructured moving grids is developed.Based on Arbitrary Lagrangian-Eulerian(ALE)equations，Discrete Geometric Conservation Law(DGCL)is constructed by adopting a new idea for modifying the volume;the field variables of new re-meshing grids are obtained by the information transfer method based on the unstructured moving grids technique;the initial shock position is determined by the flow field captured by the first-order spatial scheme and the unsteady flow is successfully simulated using shock-fitting technique.The fluid-structure coupled process of hypersonic fairing separation when Mach number reaches 6.0 is simulated using the shock-fitting and shockcapturing methods respectively，and the simulation results are good in agreement.With Mach number increased，the accuracy is hard to reach second-order unless by adjusting the limiter parameters or time step artificially.However，there is no abnormal occurring even if the Mach number reaches to 20.0 when the shock-fitting method is adopted.Comparing with the traditional shock-fitting technique，the unsteady shock-fitting technique can be used to simulate the irregular shock produced by complex shapes and the moving shock wave produced by the unsteady flow，it can also solve the stability problem which may generally occurred in the process of simulating the multi-body separation by the finite volume method(FVM ).

shock-fitting;unstructured moving grids;unsteady flow;hypersonic

V211.3

Adoi:10.7638/kqdlxxb-2014.0109

0258-1825(2015)01-0010-07

2014-09-18;

2014-10-12

劉君(1965-)，男，教授，博士，從事空氣動力學教學和計算流體力學研究。E-mail:liujun65@dlut.edu.cn

劉君，鄒東陽，徐春光.基于非結(jié)構(gòu)動網(wǎng)格的非定常激波裝配法［J］.空氣動力學學報，2015，33(1):10-16.

10.7638/kqdlxxb-2014.0109.Liu J，Zou D Y，Xu C G.An unsteady shock-fitting technique based on unstructured moving grids［J］.Acta Aerodynamica Sinica，2015，33(1):10-16.