SOLO分類理論在高中數學作業批改中的應用*

劉綠芹

近年來，隨著高考競爭壓力的增大，很多學校都非常重視數學訓練，通過大量的作業練習來訓練學生，但教師對學生作業的批改卻成為被忽略的環節。當前作業批改的主要方式是給學生打分數，對學生解答過程的深層次分析和研究很少。因此，我們需要在作業批改中引入一種新方法，不僅要對學生作業進行量化評價，更重要的是進行質性評價，并對學生的思維層次進行劃分，同時展開相應的分析和研究，為學生訂正作業、教師針對性地評講作業打下基礎。

一、什么是SOLO分類理論

SOLO分類理論是一種學生學業評價方法。“SOLO”是英文“Structure of the Observed Learning Outcome”的縮寫，其意為可觀察的學習結果的結構[1]，該理論是一種以等級描述為特征的質性評價方法。香港大學教育心理學教授Biggs，J.B在1982年與Collis，K.F合作出版的《Evaluating the Quality of learning——the SOLO taxonomy》一書中及他在1986年的《The SOLO taxonomy》一文對該理論做了詳細的應用介紹[1]。從國內外的研究發現，SOLO分類理論可以應用到多種學科領域中，包括數學、語文、英語、歷史、生物、化學、地理等，這是SOLO分類理論的優勢所在。

二、SOLO分類理論在高中數學作業批改中的應用舉例

根據SOLO分類理論，我們將學生作業劃分為五個認知水平：前結構水平（P）、單一結構水平（U）、多元結構水平（M）、關聯水平（R）、擴展抽象水平（E）。因此，在作業批改時，我們可以在學生作業的每一道試題上，打上“P、U、M、R、E”這樣的字母符號，對學生的每一道作業做出思維層次水平評價。

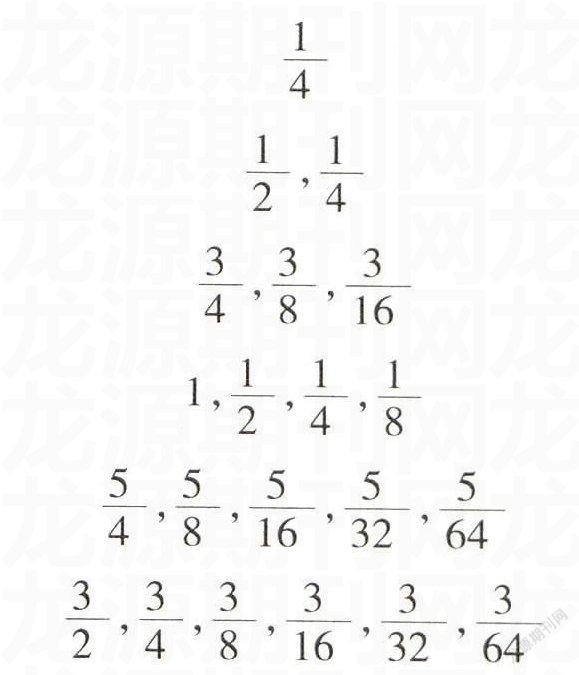
【例】已知一個“三角形數陣”，記第i行第j列的數為aij（i≥j；i，j∈N*）

（1）求a86；

（2）寫出aij關于i，j的表達式；

（3）記第n行的各數和為An，求數列{An}的前m項和Sm的表達式

■

■，■

■，■，■

1，■，■，■

■，■，■，■，■

■，■，■，■，■，■

1.試題分析

上題是筆者在教學實踐過程中布置給學生的一道作業，該題把“三角數陣”當作問題情境和背景，需要學生從中尋找有效信息和規律，并將其抽象建模為數學問題。從題設中“第i行第j列的數為aij”可以看出，需要學生對n與an的關系有深刻的認識，否則無法理解aij。從題中給出的三小問可以看出，題目是在步步引導學生，從求a86這一特殊值，到“寫出aij關于i，j的表達式”這樣的通式，再到第（3）問的Sm，層層遞進，難度也逐步加大。如何從數陣中捕捉出重要信息是解決本題的關鍵，我們從每一行給出的數可以知道，從第3行起，每一行都是一個等比數列，并且公比都為■，因此，想要求出數陣中的數，只需要再觀察每一行的第一個數組成的數列即可，即{ail}具有什么性質，當我們將這些數放在一起觀察時，我們就會發現，每一行第一個數組成的數列是{■，■，■，■，■…}，即{ai1}是首項為■，公差為■的等差數列。因此，觀察出“等比數列”和“等差數列”是解決本題的關鍵，這需要學生具有對數列的敏銳觀察能力和數據的抽象能力，同時還需要對等差數列、等比數列的概念有比較深刻的認識。接下來，需要學生對抽象出來的數學知識進行加工和分析，解決相應的問題。

第（1）問中，學生首先需要利用{ai1}是等差數列求出a81，并將其當作等比數列的第一項，求出第6項，即a86。該問只要學生抽象出數表中的核心即可解決。對于第（2）問，學生可以在第（1）問的基礎上，同樣是先利用等差數列求出ai1=■+（i-1）■=■，并將其當做第i行數列的首項，接著利用等比數列的通項公式求出aij。第（1）問是第（2）問的臺階，學生只要將第（1）問理解深刻，第（2）問就水到渠成。

對于第（3）問，則需要學生對“求和”有深刻的認識，An是求和，Sm也是求和，但An加上“{}”后則意義發生一定的改變，變成所謂的“通項公式”了。因此，求出“通項公式An”尤為重要，因為每一行都是等比數列，An的本質又是等比數列的求和，即An=■，又an1=■，故An=■-■·■，則Sm=A1+A2+…Am。我們通過觀察，An由兩部分組成，一部分是“■”，另一部分是“■·■”，那么在求Sm時，我們可以將其拆分為兩部分，即Sm=■（1+2+…+m）-■（■+■+■+…■），不難看出，第一個括號內是等差數列求和，比較容易解決。而第二個括號內比較復雜，我們令Tm=■+■+■…+■■，此時我們發現，分子可以組成一列等差數列，分母則可以組成等比數列，由此我們使用“錯位相減法”求和，即在Tm=■+■+■+…+■兩邊分別乘以■得■Tm=■+■+…+■+■，再用Tm-■Tm得■Tm=■+■+■+…+■-■=1-■，最后將其帶入Sm即可得出最后結果Sm=■+■-1。從第（3）問的解題思路來看，即有等差數列的求和，又有等比數列的求和，而且運用到“等差乘等比型數列（設{an}為等差數列，{bn}為等比數列，則數列{an·bn}可稱為等差乘等比型數列）”的求和方法“錯位相減法”，解題所用知識幾乎覆蓋到數列的每一個知識點，思維方法也要求較高，這對學生來說，是個不小的挑戰。

2.學生作業分析

（1）前結構水平

下面是某位學生的解答過程，從解答來看，他判斷出了i=8，j=6但a86究竟是什么含義，未能看懂，只是將8與6相加得a86。因此，類似于下面的答案被劃分為前結構水平（P）。

解：i=8，j=6，則a86=14

（2）單一結構水平

從下面學生的解答過程來看，該生能夠判斷出aij的含義，并且觀察出一些數成等差數列，一些數成等比數列，也求出d=■，q=■。但學生卻就此收斂，未能進一步研究下去，只解決了簡單的單一問題。因此，下面的答案可以劃分為單一結構水平（U）。

解：各行第一個數組成等差數列，a11=■，a21=■故d=■，各行數組成等比數列，a31=■，a32=■，故q=■

（3）多元結構水平

該題第（1）問中，要求第8行第6列的數是多少，在學生答案中，有很多學生是通過續寫出第7行、第8行，然后觀察a86是多少。這不失為一個好辦法，但這樣的辦法對解決第（2）問、第（3）問卻沒有大的幫助。我們需要從中找出規律，再利用數列的知識計算出相應的項。下面是某同學的解答過程，他首先判斷出ai1為等差數列，故能求出a81，又發現從第三行起，每一行又成等比數列，故求出了q=■，從而a86得解。從過程來看，該生具有一定的觀察能力，能夠從數陣中找出等差數列、等比數列，并且同時利用等差數列和等比數列的知識求解出a86。故下列答案被劃分為多元結構水平（M）。

解：數列{ai1}為等差數列

a11=■，a21=■，d=a21-a11=■，a81=■+7×■=2

又從第三行起分別成等比數列，公比都相等

q=■=■，∴a86=2×（■）5=■

（4）關聯結構水平

該題中的等差數列與等比數列在三角形數陣中看似一個橫向、一個斜向，但如何將等差數列與等比數列相關聯是本題的難點。而題目中的第一小問求a86，則相當于臺階，幫助學生理解問題。一旦學生理解了ai1為等比數列的首項功能后，求解aij則不再是難點。從下面學生的解答來看，該生顯然理解了問題的本質，首先利用等差數列求出了ai1，再以ai1為首項，■為公比，求出了aij。在解題過程中，該生很好地把等差數列、等比數列相融合，并成功解決了問題。因此，下面的答案我們劃分為關聯結構水平（R）。

解：（1）由數陣知，數列{ai1}為等差數列

∵a11=■，a21=■，∴公差d=a21-a11=■

∴a81=■+7×■=2，

又∵第三行起各行分別成等比數列，公比都相等

∴公比q=■=■，∴a86=2×（■）5=■

（2）由（1）知，ai1=■+（i-1）■=■，

∴aij=ai1·（■）j-1=■·（■）j-1=i·（■）j+1

（5）擴展抽象水平

對于第（3）問，該題要求較高，Am其實是第n行各數的和，但加上{}后，則變為新數列，題目中的Sm卻是{Am}的前m項和。從下面學生的解答來看，該生先求出An，提取■后，構成等比數列求和，并且最后化簡為■+■·■備用。接著把Sm表示成（■+■+…+■）-■（1×■+2×■+…+m×■），從中我們可以發現，前一個括號提取后，構成等差數列求和，而后一個括號內卻“既有等差數列又有等比數列”，于是該生采用的方法是將該括號內的內容提取出來，記為Tm，然后利用兩邊同時乘以所謂公比■，再與原式相減得出■Tm，進而求出最終的Sm。從該生的整個解題過程來了，首先在求解An時，通過提取■的方法，擴展出一個等比數列求和，在求解Sm時，該生又將Am裂項，擴展為兩部分，其中前一部分為等差數列，后一部分為“等差乘等比型數列”。對于后一部分，該生將等比數列求和公式的推導過程抽象至此，從而致使問題得到解決。因此，下面的解答過程，可以將其劃分為擴展抽象水平（E）。

解：（1）a81=■+7×■=2，a86=2×（■）5=■

（2）aij=[■+（i-1）×■]×（■）j-1=■·（■）j-1

（3）An=■[1+（■）1+（■）2+…+（■）n-1]

=■·■=■·[1-（■）n]

=■-■·■

則Sm=A1+A2+…+Am =（■+■+…+■）

-■（1×■+2×■…+m×■）

=■

-■（1×■+2×■…+m×■）

記Tm=1×■+2×■…+m×■） ①

則■Tm=1×■+2×■+…+m×■②

②-①得■Tm=■+■+■+…+■+■

=■-m×■

=1-（■）m-■

故Sm=■-■Tm=■[1-（■）m-■]

=■+■-1

通過上述的實踐應用發現，在數學作業批改中，我們只需在傳統的打分模式上，對學生的每一道作業試題再深入分析研究，并對照SOLO分類理論的五個層次水平（P、U、M、R、E），給學生打出相應的等級水平。當學生看到自己的等級水平時，就會思考怎樣達成更高等級水平，由此激發學生深入學習的欲望，促進學生認知水平的不斷提高。教師也可以通過班級的整體認知水平，決定作業講評的側重點，從而提高課堂教學的有效性、針對性。

參考文獻

[1] Biggs，J.B， Collis，K.F.Evaluating the Quality of Learning： The SOLO Taxonomy [M]. New York： Academic Press，1982.

【責任編輯 郭振玲】