一種改進的周期長碼擴頻序列盲估計方法研究*

熊 剛，彭 勃

(中國電子科技集團第三十研究所，四川 成都 610041)

一種改進的周期長碼擴頻序列盲估計方法研究*

熊 剛，彭 勃

(中國電子科技集團第三十研究所，四川 成都 610041)

提出了一種周期長碼DSSS信號擴頻序列盲估計改進方法。首先把周期長碼DSSS信號建模為虛擬多用戶分段系統，周期長碼序列可轉化為多個都含有模糊矩陣的短碼結構；然后采用基于二階統計量的思路，從矩陣中提取信息去除模糊的影響，并估計得到原始的擴頻碼序列。通過對該思路的進一步改進，成功應用到多徑環境盲估計方法中；最后通過計算機仿真結果驗證了該算法的有效性，其性能優于以前的方法。

直接序列擴頻 周期長碼 盲估計 多徑信道

0 引 言

直接序列擴頻(DSSS， Direct Sequence Spread-Spectrum)信號在安全保密通信系統、低軌衛星系統、全球定位系統、碼分多址CDMA系統等軍用和民用領域中都有廣泛應用[1]。擴頻通信發射機在發送數據之前先采用偽隨機(pseudo-noise，PN)序列對基帶信號進行調制，直接序列擴頻信號的帶寬遠大于基帶帶寬，并且信號的功率譜密度通常很低。擴頻碼序列是直接序列擴頻信號重要參數。一般來說，可以分為短碼調制擴頻和長碼調制擴頻兩種，短碼調制是指一個周期的擴頻碼序列只調制一位信息碼；而長碼擴頻信號的擴頻周期大于信息碼周期，即一個周期擴頻碼調制多位信息碼。長碼調制DSSS信號不僅可以抑制部分符號間干擾，也具有更好的保密性能；另一方面，使得在通信對抗和網絡安全監控系統中對DSSS信號進行分析的難度增大。此外，對于多徑信道環境和多用戶情況，因為信道衰落和多址干擾對信號有較大影響[2]，所以這也是擴頻碼序列盲估計研究中的一個難點。

目前，對于DSSS信號擴頻碼序列的盲估計，已經提出了一些基于子空間的分析方法，但多數只適用于短碼調制，不能直接應用在周期長碼DSSS序列盲估計中。為解決上述問題，本文基于將周期長碼DSSS信號模型進行轉化和二階統計量的計算優化等思路，提出了一種改進的周期長碼擴頻序列的盲估計方法，并將該方法擴展到了多徑信道環境下。

1 信號模型分析

接收信號的基帶模型如圖1所示：

如前所述，DSSS周期長碼不同于短碼，每個周期由多個符號組成。設c(t)表示擴頻碼序列，擴頻序列含G個數據符號，符號持續時間為Ts。設信息碼序列{[s(k)]}獨立同分布，w(t)表示高斯白噪聲。周期長碼DSSS信號的表達式如下

(1)

此處cu(t)定義為

(2)

su[k]s[Gk+u-1]u=1,…,G.

(3)

在式(1)中，周期長碼DSSS信號與虛擬多用戶系統模型是等效的，如圖2所示。

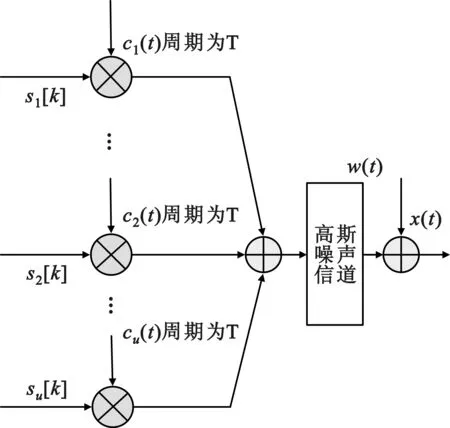
圖2 周期長碼擴頻信號等效多用戶模型

設第u個用戶(u=1,2,…,G)擴頻碼表示為cu(t)，數據速率為1/T。設信號采樣周期為T/p。信號的離散形式可表示為

x[n]x(nΔ),c[n]c(nΔ),cu[n]cu(nΔ),w[n]w(nΔ).

(3)

還可表示為信號的過采樣形式，如下

(4)

其中

(5)

且

(6)

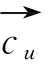
(9)

其中，設m為整數，且m=p/G。在上式中，C是一個塊對角滿秩矩陣。下面將利用該特征進行擴頻碼估計，設信號和噪聲序列是零均值的，因此相關矩陣分別為

(10)

(11)

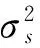
(12)

2 改進的周期長碼序列估計方法

將式(12)中的Rx進行特征值分解，可表示為

(13)

其中，U是特征向量矩陣，Λ是特征值矩陣，由此得到：

(14)

上式中，信號子空間的維數是G，因此，信號子空間是由前面的G列特征向量構成的，噪聲子空間則由剩余的p-G個特征向量構成。矩陣U即可表示為

(15)

其中，U(s)是代表信號子空間特征向量的矩陣，U(n)是代表噪聲特征向量的矩陣。假如信號子空間對應的特征值是各不相同的，則U(s)等價于C。在這里，考慮到Cu在{1,-1}集合中取值以及式 (9)中的碼序列結構，則有

‖c1‖=‖c2‖=…‖cn‖

(16)

因此，前面G個特征值是相等的，并且可得出以下關系式

(17)

其中，Q是歸一化的模糊矩陣。

對于以前一些方法而言，由于存在模糊矩陣，如果沒有先驗信息是不可能從二階統計量(SOS)中估計出C的。但改進后的新方法可以通過等價為各用戶短碼信號和一些推導運算估計得到周期長碼DSSS擴頻序列的結果C，算法思路如下。

從式(16)中可得出

C=U(s)Q

(18)

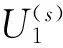
(19)

顯然有C1的秩為G-1，即rank(C1)=G-1。因此還可得出

(20)

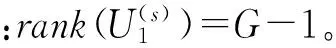
(21)

因此，qG的表達式為

(22)

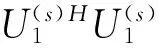
(23)

從而可得到

(24)

(25)

因此

(26)

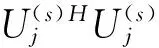
(27)

其中Vj表示特征向量矩陣，Λj表示特征值矩陣。Vj還可表示成

(28)

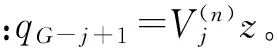
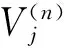
Qj[qG-j+2,q2,…,qG]

(29)

由于Q是歸一化矩陣，故有

(30)

將式(28)代入式(30)，可得

(31)

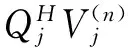
(32)

通過將z代入式(28)并推導，可得到向量qG-j+1。繼續采用該思路，還可估計出矩陣Q全部G-1列。為求出Q的第一列，可通過下式得到

(33)

按照這種方法，q1可通過下式得到

(34)

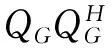
下面分析將該算法應用于多徑信道環境。在圖3中，可得到一個等效多用戶模型。

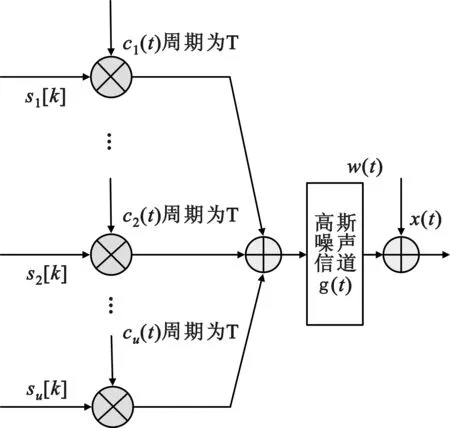
圖3 多徑信道周期長碼信號等效模型

但與一般的多用戶系統不同，各用戶占用一個信道且它們都是同步的。因此，該模型類似于CDMA下行鏈路。由此，信號表達式可表示為

(35)

其中，g(t)是信道的響應，對于各虛擬用戶而言都是相同的。設

(36)

其中hu(t)是cu(t)和信道響應g(t)的卷積。目的是為了估計出hu(t)，u=1,2,…,G，從而能進行信道均衡同時對擴頻信號解擴。考慮到信道響應的持續時間有限，并假設

hu(t)=0，t>(M+1)T,t<0

(37)

信道的離散模型可表示為如下

(38)

還可以簡化表示為

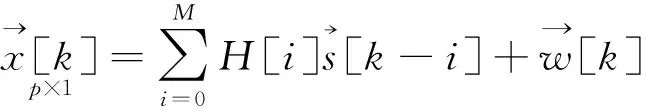
(39)

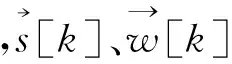
(40)

為方便，可將接收信號的連續窗看作為一個長為L的塊矩陣，并定義下列向量為

(41)

(42)

(43)

通過以上定義式，接收信號中的Lp×1向量可以表示為

(44)

其中ΓL(H)是一個Toeplitz塊矩陣，可定義為

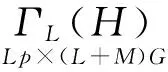
(45)

(46)

過去有一些可應用于多徑信道的估計算法，例如線性預測的方法等，但它們的性能還需進一步改進[3]。下面引入一種通過矩陣結構特征能夠很好實現消除模糊關系和特征值分解的思路，即酉矩陣方法，可以從Rx中估計出Ψ，并去除模糊矩陣Q。該思路首先需構造一個酉矩陣的形式，如下

(47)

其中，Ψ可定義如下

Ψ(H[0]T,H[1]T,…,H[M]T)T

(48)

矩陣Ψ各列是各虛擬用戶的擴頻碼與其共用的多徑信道之間的卷積。在這種情況下，根據式(2)和(37)，Ψ能表示成如下形式

(49)

其中，符號0m×1表示維數m×1的全零矩陣。

Ψ可表示成如下：

Ψ=[φ1,φ2,…,φG]

(50)

然后可得出如下特征表達式

φu[n]=0 n<(u-1)m,u=1,2,…,G

通過利用矩陣Ψ的特征，可以估計出Q。因此，Ψ也可由下式估計得

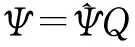
(51)

(52)

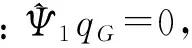
(53)

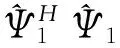
(54)

(55)

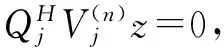
3 性能仿真和分析

首先對根據前面所述的周期長碼DSSS信號虛擬多用戶模型推導出的公式(2)～(9)進行仿真，驗證算法對周期長碼序列的各分段用戶擴頻碼的估計結果。

圖4第一行表示原始各分段虛擬用戶擴頻碼序列，圖4第二行表示通過本文的改進后的算法得到的結果，該分段序列從圖中可以看出估計是正確的。

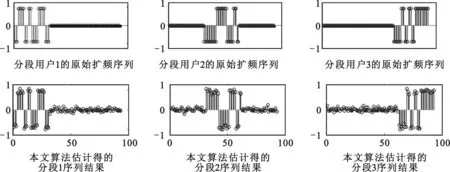
圖4 信噪比0 dB時各分段原始序列及估計結果

下面對多徑信道環境中采用本文算法與傳統子空間方法進行性能仿真。這里引入序列的互相關系數作為衡量算法估計性能的指標。互相關系數是指兩個碼序列之間相似性的量度。具體是指算法估計得到的碼序列與原始擴頻碼序列逐比特比較時，一致的數目減去不一致的數目。可用下式表示

(56)

其中，A是估計擴頻碼序列結果x和原始擴頻序列y里面碼元相同數目，D是碼元不同數目，p是擴頻序列碼元總數。Rxy數值越大，估計擴頻序列準確度越好。圖5表示本文算法與傳統算法性能仿真曲線。橫軸表示信噪比，縱軸表示擴頻序列估計結果與原始序列互相關系數，其余參數如前所述。

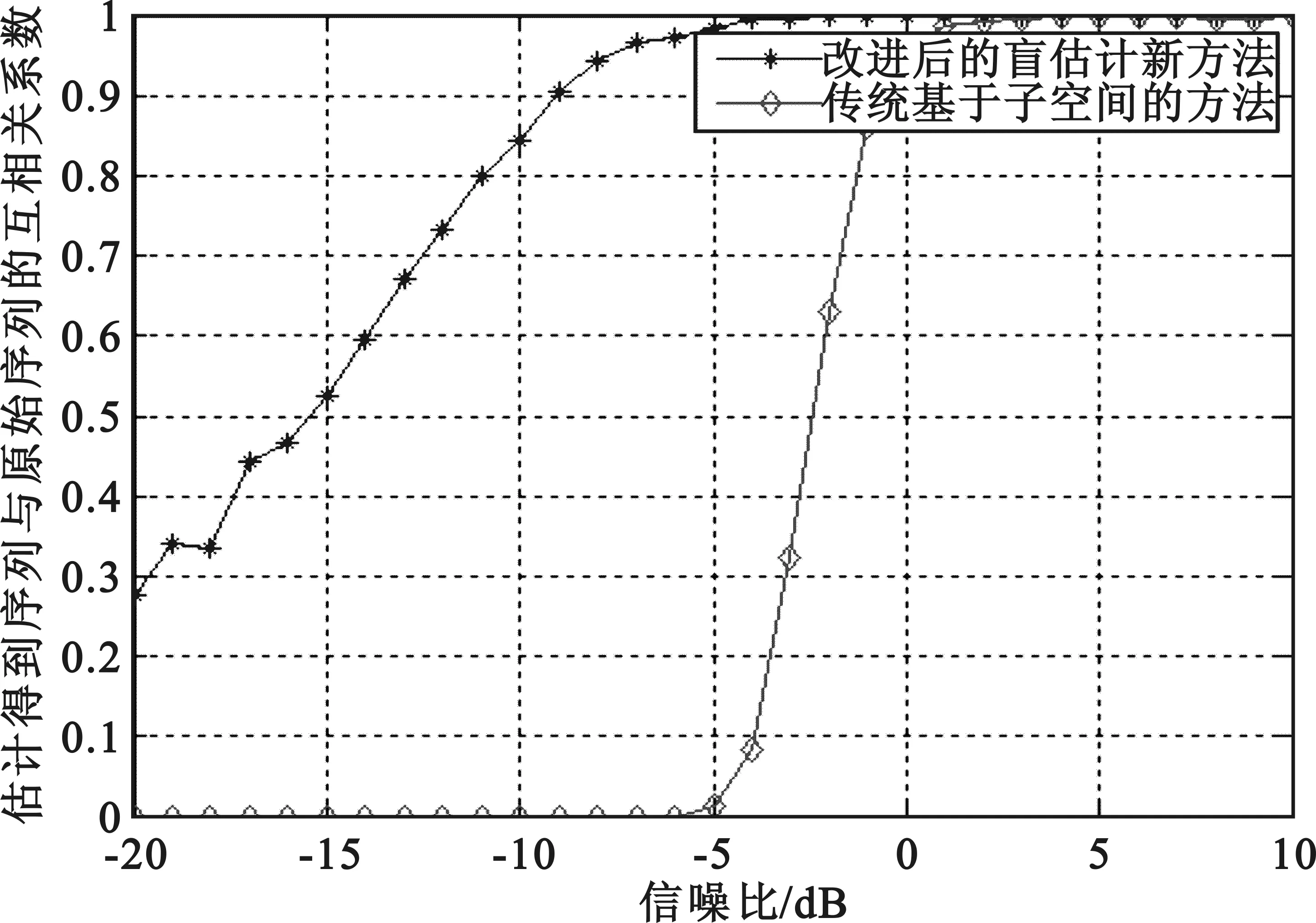
圖5 本文方法與傳統方法的性能對比曲線

從上圖中可以看出，在信噪比較低的情況下，新算法的性能要優于傳統的基于子空間的算法，而且新算法在信噪比為-2dB左右時，估計結果與原始序列的互相關系數為1。

4 結 語

本文利用虛擬多用戶分段模型與二階累積量等思路，提出了一種改進的周期長碼擴頻序列盲估計方法，并將該算法進一步擴展應用到多徑信道環境中。該方法還增強了對噪聲抑制能力，通過計算機仿真驗證了該算法的性能，在信噪比達到-2 dB以上時可正確進行DSSS信號周期長碼擴頻序列的估計。今后將進一步優化，為解決低信噪比下DSSS信號擴頻序列估計以及盲解擴問題提供一種更有效的手段，也使直接序列擴頻通信的監測和對抗技術發展發揮更重要的作用。

[1] 曾璐,謝曉堯. 基于MATLAB擴頻通信系統誤碼率的研究[J].通信技術,2011,44(11):25-29. ZENG Lu, XIE Xiao-yao . Study on Bit Error Rate of Spread Spectrum Communication by MATLAB.[J] Communications Technology. 2011, 44(11):25-29.

[2] J. Ma, “Blind Equalization and Multiuser Detection of DSCDMA signals In Multipath Channel,” Ph.D. dissertation, Auburn University, Alabama, December , 2002.

[3] C. Nsiala Nzeza, R. Gautier, and G. Burel, “Blind synchronization and sequences identification in CDMA transmissions,” in IEEE-AFCEA MILCOM, California, USA, November 2004.

[4] 林智慧,陳綏陽,王元一. m序列及其在通信中的應用[J].現代電子技術,2009,44(08):49-55. LIN Zhi-hui, CHEN Sui-yang. M-Sequence and Its Application in Communication [J].Modern Electrical Technology, 2009, 44(08):49-55.

XIONG Gang(1982.5-), male，M.Sci.，engineer, mainly working at wireless network security and signal processing technology.

彭 勃(1977.8-)，男，碩士，高級工程師，研究方向：無線網絡安全技術與信號處理技術。

PENG Bo (1977.8—), male， M.Sci.，senior engineer, mainly working at wireless network security and signal processing technology.

A Modified Blind Estimation in PLC DSSS Communications

XIONG Gang, PENG Bo

(No.30 Institute of CETC, Chengdu Sichuan 610041, China)

This paper proposes a method of blind estimation for PLC (Periodic Long Code) DSSS (direct sequence spread spectrum) signal. Firstly, PLC DSSS signal is modeled as a virtual multi-user system,and PLC sequence can be converted to several short-code structures with ambiguity matrix. Then, based on the idea of SOS (second-order statistics), influence of ambiguity matrix is removed and the original spreading codes sequence also estimated.The modified algorithm is successfully applied to blind estimation in multipath environment. Finally, computer simulation verifies the efficiency of this modified algorithm and indicates that its performance is better than that of original one.

DSSS; periodic long-code; blind estimation; multipath channel

S接收信號模型示意圖Fig.1 Model of

DSSS signal

10.3969/j.issn.1002-0802.2015.03.006

2014-09-10；

2014-12-25 Received date:2014-09-10；Revised date：2014-12-25

TN918.91

A

1002-0802(2015)03-0272-06

熊 剛(1982.5-)，男，碩士，工程師，主要研究方向：無線網絡安全技術與信號處理技術；