傅里葉變換的行波型中空超聲電機的系統效率*

牛子杰，孫志峻，吳金濤，張 軍，張激揚，梁大志

(1.南京航空航天大學機械結構力學及控制國家重點實驗室 南京，210016) (2.北京控制工程研究所 北京，100190)

?

傅里葉變換的行波型中空超聲電機的系統效率*

牛子杰1，孫志峻1，吳金濤2，張 軍1，張激揚2，梁大志1

(1.南京航空航天大學機械結構力學及控制國家重點實驗室 南京，210016) (2.北京控制工程研究所 北京，100190)

由于行波型中空超聲電機的驅動信號為高壓、高頻信號，因此，由行波型中空超聲電機及其驅動器組成的系統的各級功率與效率不容易獲取，這些因素均影響到后續對行波型中空超聲電機性能的研究。針對此問題，首先，通過傅里葉變換的方法對超聲電機驅動信號進行處理，構建了電機及其驅動系統各級效率的計算方法；然后，通過實驗獲取了行波型中空超聲電機及其驅動器組成的系統的效率，并進一步研究了驅動頻率、驅動電壓及諧振匹配點對系統效率的影響。實驗表明：驅動頻率越靠近諧振頻率，系統總效率越高；驅動電壓越大，系統總效率越高；驅動電路匹配的諧振點遠遠高于電機機械諧振頻率，使得驅動信號頻率介于電路諧振頻率和機械諧振頻率之間時系統的效率最高。

傅里葉變換； 超聲電機； 系統效率； 諧振頻率； 匹配電路

引 言

與電磁電機相比，超聲電機具有大力矩、低轉速、能量密度大、響應速度快、定位精度高、無電磁干擾、斷電自鎖等優點。隨著光學工程、航空航天和精密制造等技術的快速發展，超聲電機這些優點越來越突出，這使得對超聲電機的需求更加迫切[1-2]。行波型中空超聲電機(簡稱中空電機)作為一種特殊的微特電機，在繼承了常見超聲電機的特點以外，中空的結構更拓寬了其使用范疇[3]。行波型中空超聲電機與其驅動器組成的是一個機電系統。由于此種電機與普通的電磁電機原理及結構差異較大，所以該種電機的驅動器與普通電磁電機驅動器的差異也比較大。

國內外很多學者都對行波超聲電機驅動功率進行了研究。上羽貞行等[4]對佳能環狀超聲電機進行了研究，總結出該種電機的等效電學模型。祖家奎等[5]研究了定子的電學特性、驅動方式及其振動性能之間的關系，提出應根據電機的輸出功率選擇合適的工作頻帶和驅動方式。史敬灼等[6]研究了行波電機驅動電路的匹配方式，給出了超聲電機串聯電感匹配電路的設計原則。然而，這些研究大部分著眼于超聲電機的某些局部，如電機本體或電機的驅動器，而對超聲電機及其驅動器組成的機電一體化系統整體的研究較少，從功率傳遞及機電一體化系統效率角度對超聲電機系統研究的更少。其主要存在如下問題：a.超聲電機驅動信號為高頻，是高壓信號，因此獲取系統各級相關功率及效率目前尚無成熟方法；b.驅動頻率、驅動電壓及電路諧振匹配點對電機系統效率的影響目前研究較少。

針對筆者在文獻[7]中提出的一種中空式行波超聲電機和文獻[8]提出的一種并聯電容式超聲電機驅動器的基礎上進行研究。首先，分析了超聲電機能量傳遞機理；其次，對超聲電機驅動信號進行實驗和數據采集；接著，在Matlab環境下對數據進行傅里葉變換處理；最后,分析數據得到此種中空電機及其驅動系統相關部分功率隨著負載變化的變化情況。

1 中空電機及其驅動器拓撲結構

1.1 中空電機結構

本研究的超聲電機是一種中空式的超聲電機，其結構如圖1所示。

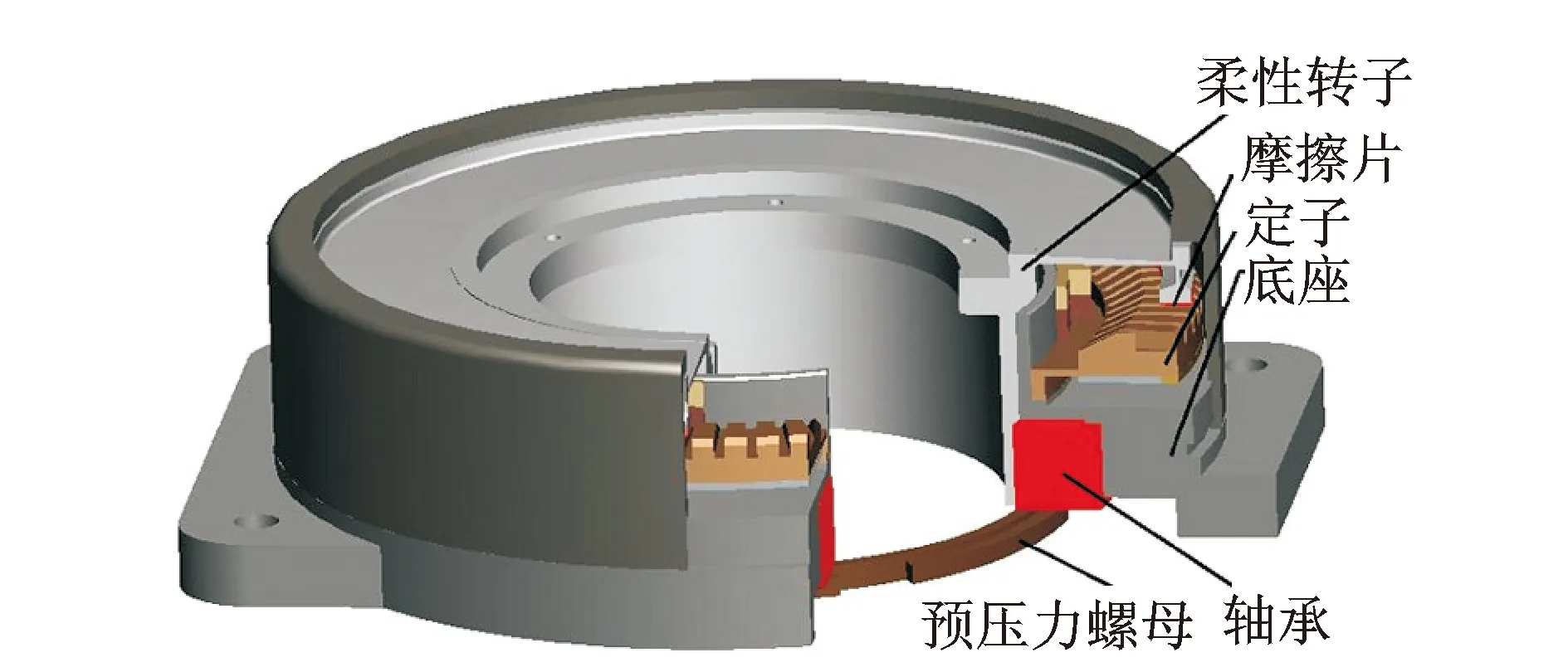
圖1 電機結構

根據圖1所示的電機結構可以看出:柔性轉子通過貼在表面的摩擦片與定子接觸；而柔性轉子下方通過螺紋與預壓力螺母連接；預壓力螺母通過軸承給柔性轉子施加拉力[9]。

1.2 并聯電容電路拓撲結構

筆者使用的驅動器為文獻[8]中所描述的驅動器，其拓撲結構如圖2所示。中空電機與驅動器之間通過4根電源線連接，其中2根驅動信號分別為sin信號和cos信號，另外兩路為地信號和孤極電壓信號。圖2所示為sin信號或者cos信號中的某一路電源信號，中空電機陶瓷片中的一項并聯于OUT和COM之間。

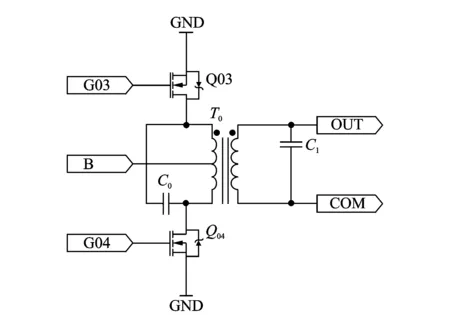
圖2 并聯電容驅動器拓撲結構

圖3所示的是中空電機與驅動器之間連接的簡圖。其中：L1和L2分別為驅動器A相和B相的變壓器副邊電感；C1和C2分別為驅動器A相和B相的并聯匹配電容；CA和CB分別為中空電機A相和B相的靜態電容。一般情況下L1=L2，C1=C2，CA=CB。

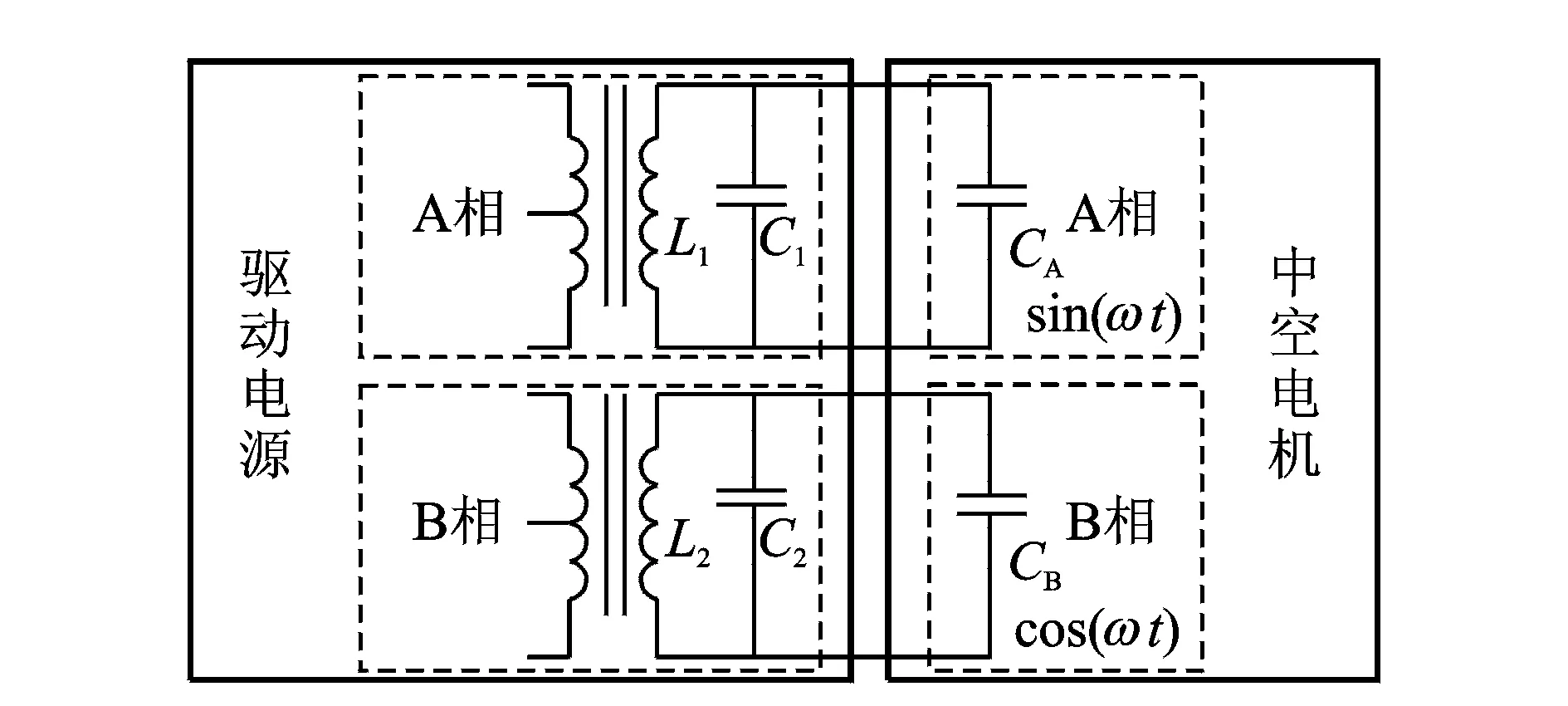
圖3 中空電機與驅動器連接簡圖

2 中空電機運行機理

2.1 定子行波的產生

筆者論述的中空行波超聲電機的振動主體(即定子)為一帶支撐板的圓環，上面有齒狀結構，其振動方程沒有解析表達式。為便于原理性分析，可把它簡化成一圓板狀結構，如圖4所示。

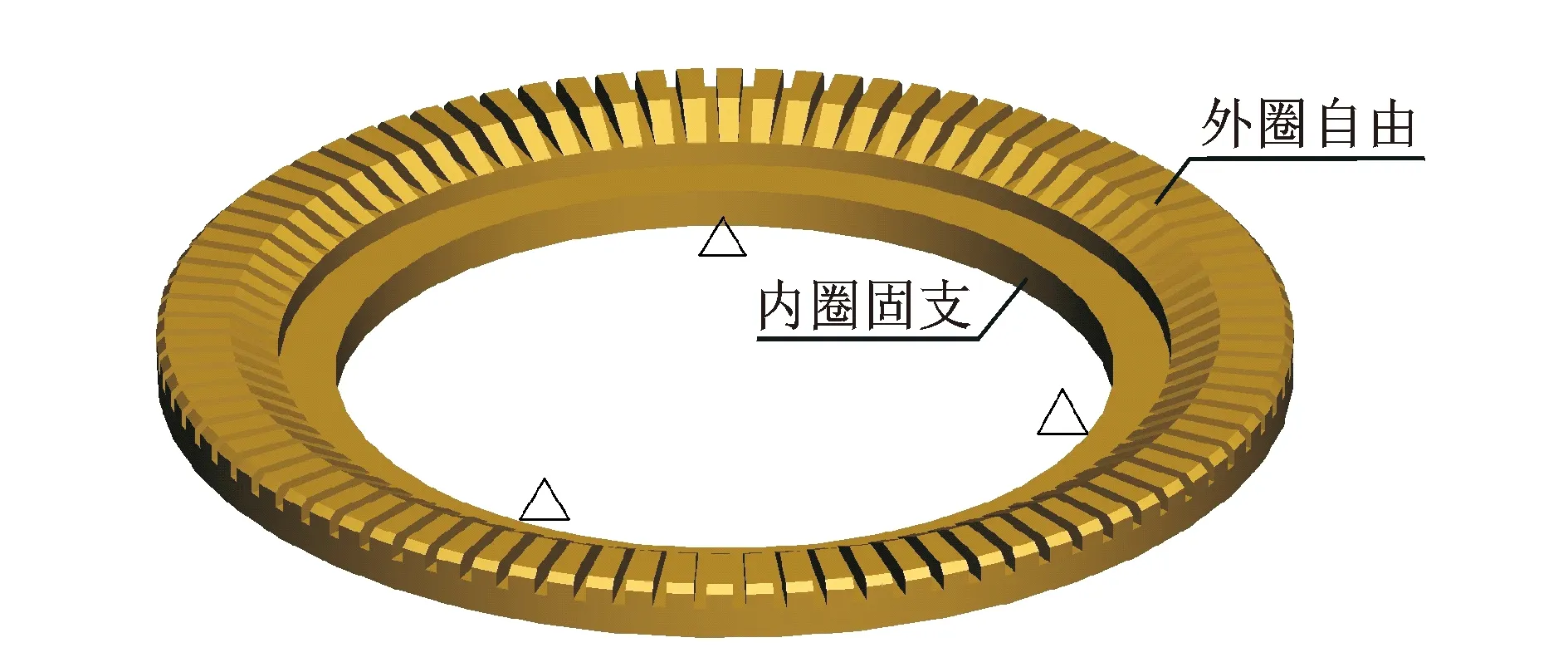
圖4 定子形狀

根據彈性動力學理論可知，對于一個平面圓板，存在如圖5所示的彎曲振動模態，其振型一般稱之為B0n，其中n為彎曲振動的波數[10-13](此例圖中波數為11)。

圖5 定子模態

用某振型函數φA(r,θ)來對該振型加以描述，稱之為A相振型

φA(r,θ)=R(r)cos(nθ)

(1)

其中：R(r)為歸一化的不同半徑處的垂向振幅函數。

在圓板最外緣R(r)值取為1，即

R(rmax)=1

(2)

設該振型的模態坐標為

qA(t)=WAcos(ωnt)

(3)

其中：ωn為對應該振型的固有頻率。

A相的駐波振動方程為

wA(r,θ,t)=φA(r,θ)qA(t)=WAR(r)cos(nθ)cos(ωnt)

(4)

由于圓板是軸對稱的，與A相振型在空間上相差任意角度的振型都是該模態的主振型[14]，取與其相差π/2的正交振型，該振型稱之為B相振型

φB(r,θ)=R(r)sin(nθ)

(5)

當B相振動的模態坐標取為

qB(t)=WBsin(ωnt+α)

(6)

則B相的駐波振動方程為

wB(r,θ,t)=φB(r,θ)qB(t)=WBR(r)sin(nθ)sin(ωnt+α)

(7)

由線性波的疊加原理，A和B兩相駐波可疊加成如下振動[15]

(8)

根據式(8)可知，圓板此時的振動由正向行波cos(nθ-ωt)、反向行波cos(nθ+ωt)和駐波cosωt組成。

1) 當α=0，WA=WB=W0時，即B相與A相同頻、等幅、空間及時間上都超前π/2時，此二駐波可疊加為一個正向(逆時針)行波

w(r,θ,t)=ξ0R(r)cos(nθ-ωt)

(9)

2) 當α=π,WA=WB=W0時，即B相與A相同頻、等幅、空間超前π/2、時間滯后π/2時，此二駐波可疊加為一個反向(順時針)行波

w(r,θ,t)=ξ0R(r)cos(nθ+ωt)

(10)

3) 當α=π/2時，圓環板中只有駐波，不形成行波。

2.2 壓電陶瓷片的極化配置

上面討論了行波產生的條件，為了滿足這些條件，以便在超聲電機定子中激發出所期望的理想行波，在定子的結構設計、壓電陶瓷的極化、配置以及施加交變電壓等方面也必須滿足特定的條件。壓電陶瓷片極化[16]如圖6所示。

1) 為產生A,B兩相駐波并滿足空間相位差π/2，通常按照圖6方式進行壓電陶瓷的極化和配置，即在A,B兩相極化了的壓電陶瓷間留有λ/4和3λ/4的空間。圖6中孤極雖然極化，但不是用來激勵定子的，其上不施加交變電壓。當其隨定子振動時由于逆壓電效應在孤極上會產生交變電壓，通過該電壓可判斷超聲電機的工作狀態，因此該電壓可供驅動和控制電路用作反饋信號，通常稱之為孤極反饋。圖7,8分別為A相和B相激勵駐波。

2) 為保證時間的相位差，需對A，B兩相壓電陶瓷分別激振，一個施加sin相交變電壓的同時，另一個施加cos相交變電壓。

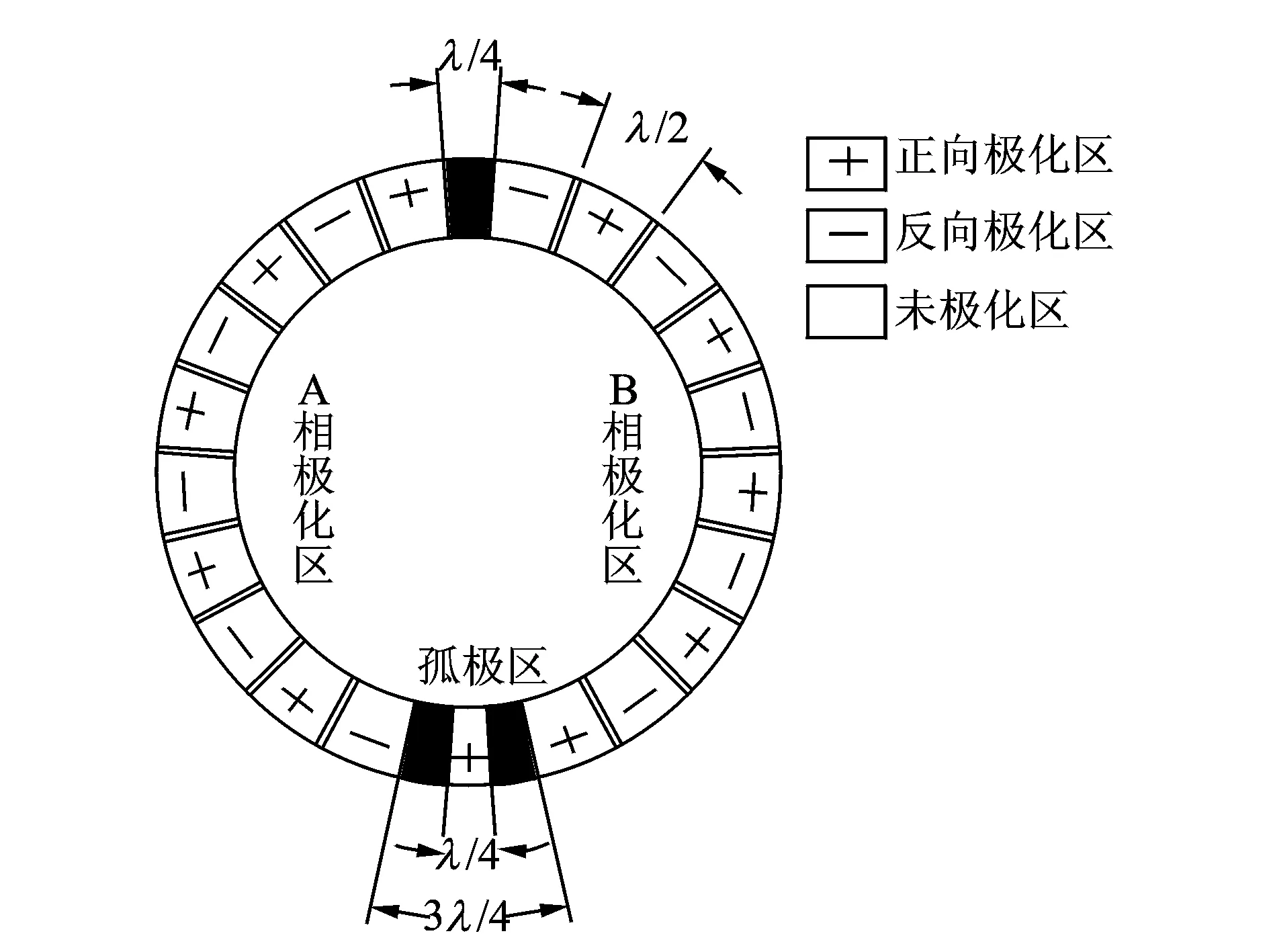
圖6 壓電陶瓷片極化

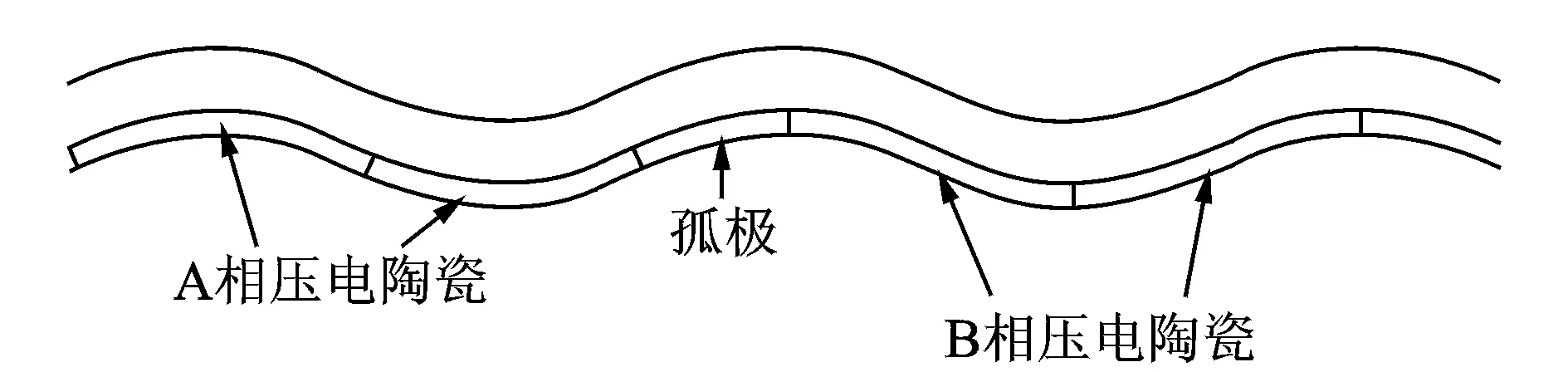
圖7 A相激勵駐波

圖8 B相激勵駐波

3 傅里葉變換

傅里葉變換將滿足一定條件的某個函數表示成三角函數(正弦、余弦函數)或者它們積分的線性組合。傅里葉變換是數字信號處理領域一種很重要的算法，其原理表明，任何連續測量的時序或信號都可以表示為不同頻率的正弦波信號的無限疊加。根據該原理創立的傅里葉變換算法利用直接測量到的原始信號，以累加方式來計算該信號中不同正弦波信號的頻率、振幅和相位。

3.1 傅里葉變換公式

由上面分析可知，中空電機的輸入信號為高頻信號，由于壓電陶瓷片需要的驅動電壓較高，因此高頻驅動信號在經過變壓、濾波之后變成了高頻、高壓信號。由于超聲電機為容性負載，電路無法做到完美匹配，因此最后得到的電機驅動信號為含有較多雜波的非正弦高頻、高壓信號，如圖9所示。該種信號如果不經過傅里葉變換，將其分解為諧振頻率的多次諧波信號，要計算得到電路中各級的功率及效率比較困難。因此,對于電機驅動信號進行傅里葉變換是后續電路效率及功率研究的基礎。

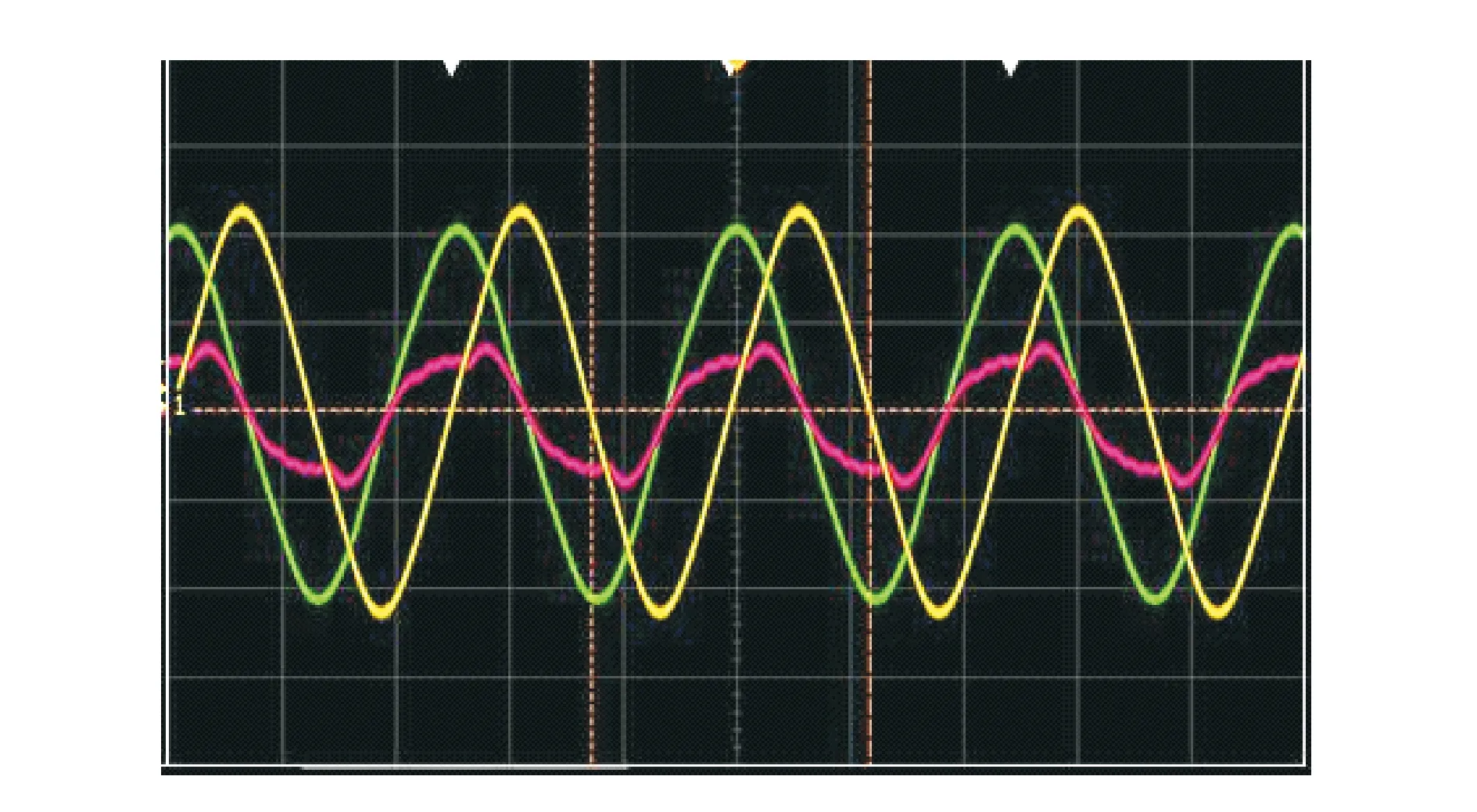
圖9 示波器顯示的電壓與電流信號

中空電機A，B兩項陶瓷片分別施加激振電壓，一個施加正弦相交變電壓信號(圖9中綠色曲線)的同時，另一個必須施加余弦相交變電壓信號(圖9中黃色曲線)。圖9中的紅色曲線為與黃色曲線對應的電流信號。筆者將中空電機A，B兩項的電壓和電流信號分別進行傅里葉變換，用到的傅里葉級數為

(11)

其中：x(t)為電壓或者電流實時信號；a0為直流分量；an和bn為n次諧波的系數；ω0為基頻。

參數a0，an和bn為

(12)

利用輔角公式將式(11)中的cos諧波和sin諧波進行合并，可得

(13)

其中：a0為信號均值，是直流分量；An為N次諧波的幅值；nω0為N次諧波的頻率；φn為N次諧波的相角。

其中，參數An和φn為

(14)

3.2 中空電機及其驅動系統各級效率的獲取

中空電機及其驅動器組成的機電系統，在負載條件下工作框圖如圖10所示。

圖10 系統能量傳遞框圖

由圖10可知，中空電機及其驅動器組成的機電系統在工作過程中涉及到的效率分別包括驅動器效率、中空電機效率和機電系統總效率，涉及到的功率分別為系統輸入功率、電機輸入功率和系統輸出功率。下面分別給出相關功率及效率的計算方法。

系統輸入功率主要通過直流電源獲取電壓和電流得到，具體如下

Pin=UinIin

(15)

電機輸入功率與驅動器輸出功率相同。如上所述，通過傅里葉變換，得到電壓和電流信號的各頻率點的分量，然后計算每個頻率點的有功功率，再將這些功率相加，最后獲得電機輸入功率。筆者在數據分析過程中獲取了傅里葉變換得到的電壓和電流信號的直流分量、一次諧波分量、二次諧波分量和三次諧波分量。分別針對每種信號求得相關的功率，具體如下

(16)

其中：P0，P1，P2，P3分別為直流分量功率、一次諧波分量功率、二次諧波分量功率和三次諧波分量功率；φU為電壓相位角；φI為電流相位角。

在獲得各諧波分量的功率之后，可獲得電機輸入功率Pdin。由于超聲電機驅動信號為兩路，因此輸入功率要乘以2

Pdin=2(P0+P1+P2+P3)

(17)

系統輸出功率主要通過輸出扭矩與轉速獲得，本系統輸出功率為

Pout=2πToutnout/60

(18)

其中：Pout為系統輸出功率；Tout為電機輸出扭矩；nout為電機輸出轉速。

在獲得相關功率之后，機電系統各模塊的效率計算相對比較簡單。式(19)為驅動器效率，式(20)為電機效率，式(21)為電機及其驅動系統總效率

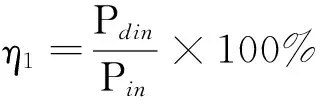
(19)

(20)

(21)

4 實驗及數據分析

4.1 實驗環境

實驗需要測試的數據包括直流電源的電壓和電流、電機輸入的兩路驅動電壓和電流、電機輸出轉速和扭矩、孤極反饋電壓。實驗裝置如圖11所示。為了消除溫度對電機性能的影響，保證數據的可靠性，本實驗在潔凈房進行，室溫為25℃。在電機進行實驗測試之前,先讓電機空轉10 min左右,以保證電機溫度達到平衡。

圖11 實驗設備

實驗裝置中：直流電源用于提供能量及測量輸入電壓和電流；測功機用于提供負載扭矩和測量電機輸出扭矩和轉速；示波器用于測量電機輸入電壓、電流計孤極電壓；電流探頭用于輔助示波器測量電機輸入電流。

4.2 數據處理

為了獲得較真實的結果，本實驗在每一個負載扭矩下采集2 000組電機輸入的電壓和電流信號,然后利用三次傅里葉變換將每個扭矩點的電壓和電流分別分解為直流分量、一次諧波分量、二次諧波分量和三次諧波分量，再分別計算功率，將計算得到電機輸入總功率。相關數據處理流程如圖12所示。

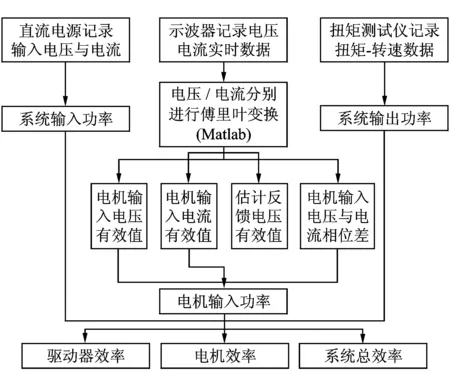
圖12 數據處理流程

數據處理包括單點處理和批量處理。單點處理是指獲得電機在某一個扭矩負載下分解得到電機輸入信號的各諧波分量，軟件界面如圖13所示。

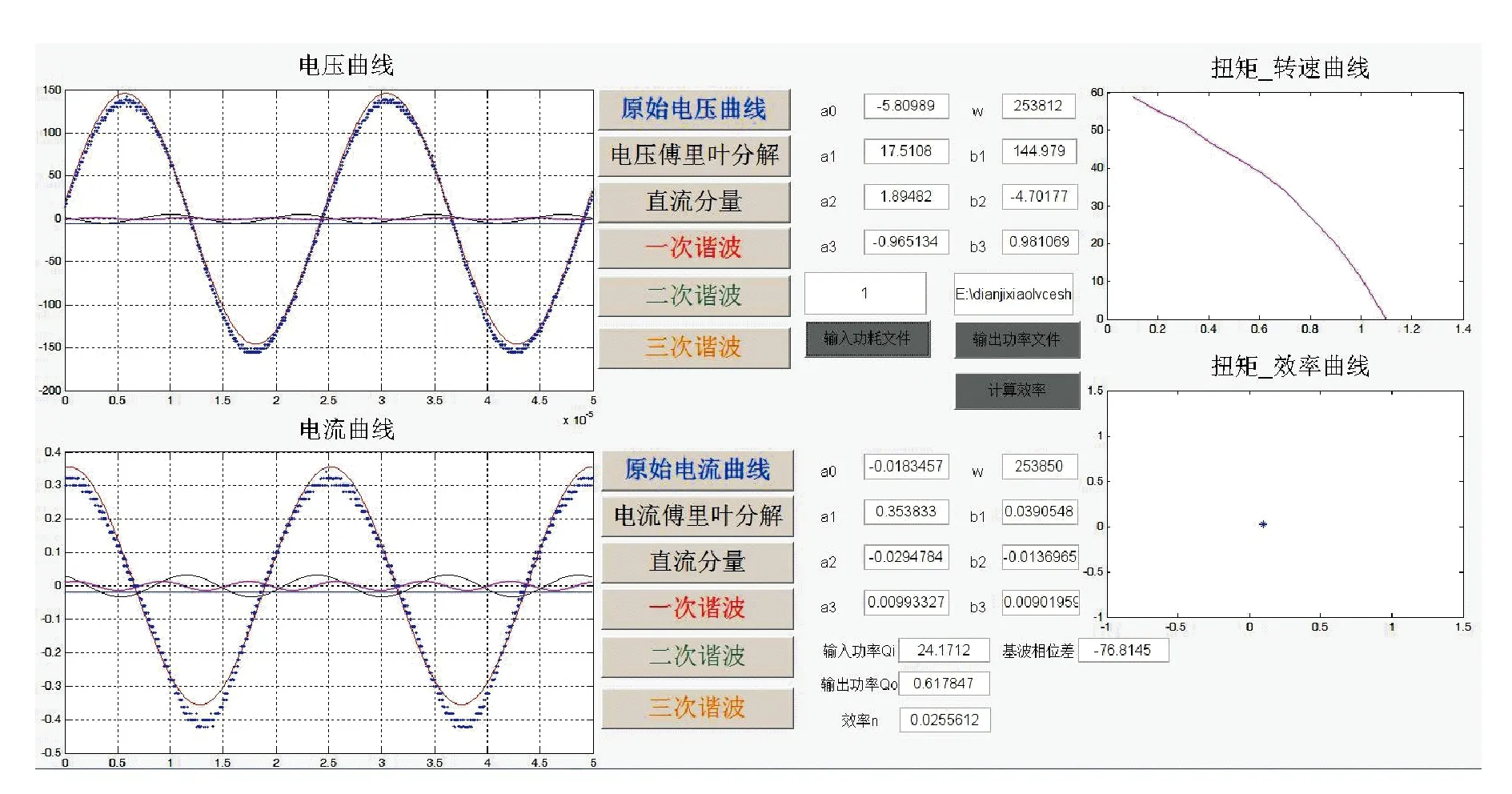
圖13 單點數據處理界面

由于每個扭矩點均記錄了2 000組數據，在整個電機性能測試實驗中數據量非常大，因此筆者通過批量數據處理軟件將電機的扭矩實驗數據批量處理為一個個表單的形式。

4.3 數據分析

筆者主要通過傅里葉變換的方法獲取了普通實驗方法較難獲取的超聲電機輸入功率，然后通過效率計算公式獲得了中空電機及其驅動系統各級效率及整體效率，同時還對驅動頻率、驅動電壓、諧振匹配點對中空電機及其驅動系統的效率影響進行了研究。本實驗所用的電機為70中空電機，其諧振頻率為39 500 Hz，正常驅動電壓峰峰值為400 V。

4.3.1 驅動頻率對系統效率的影響

行波超聲電機調頻調速是最常見的一種形式，電機及其驅動系統在不同驅動頻率下效率如何變化也成為關注的焦點。實驗獲取了70中空電機及其驅動器在不同的驅動頻率下的系統總效率，實驗結果如圖14所示。由圖可知,中空電機及其驅動系統總效率受到驅動頻率的影響較大，驅動頻率越靠近諧振頻率，電路總效率越高，電機輸出扭矩越大。

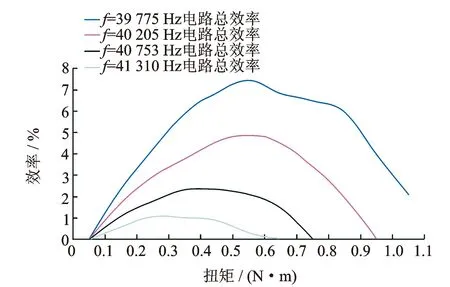
圖14 驅動頻率對系統效率的影響

4.3.2 驅動電壓對系統效率的影響

行波型超聲電機調壓調速也是一種常見的調速形式。筆者研究了70中空電機在40 500 Hz的固定頻率下驅動電壓峰-峰值在250～400 V變化時系統的輸出功率的變化情況,實驗結果見圖15。

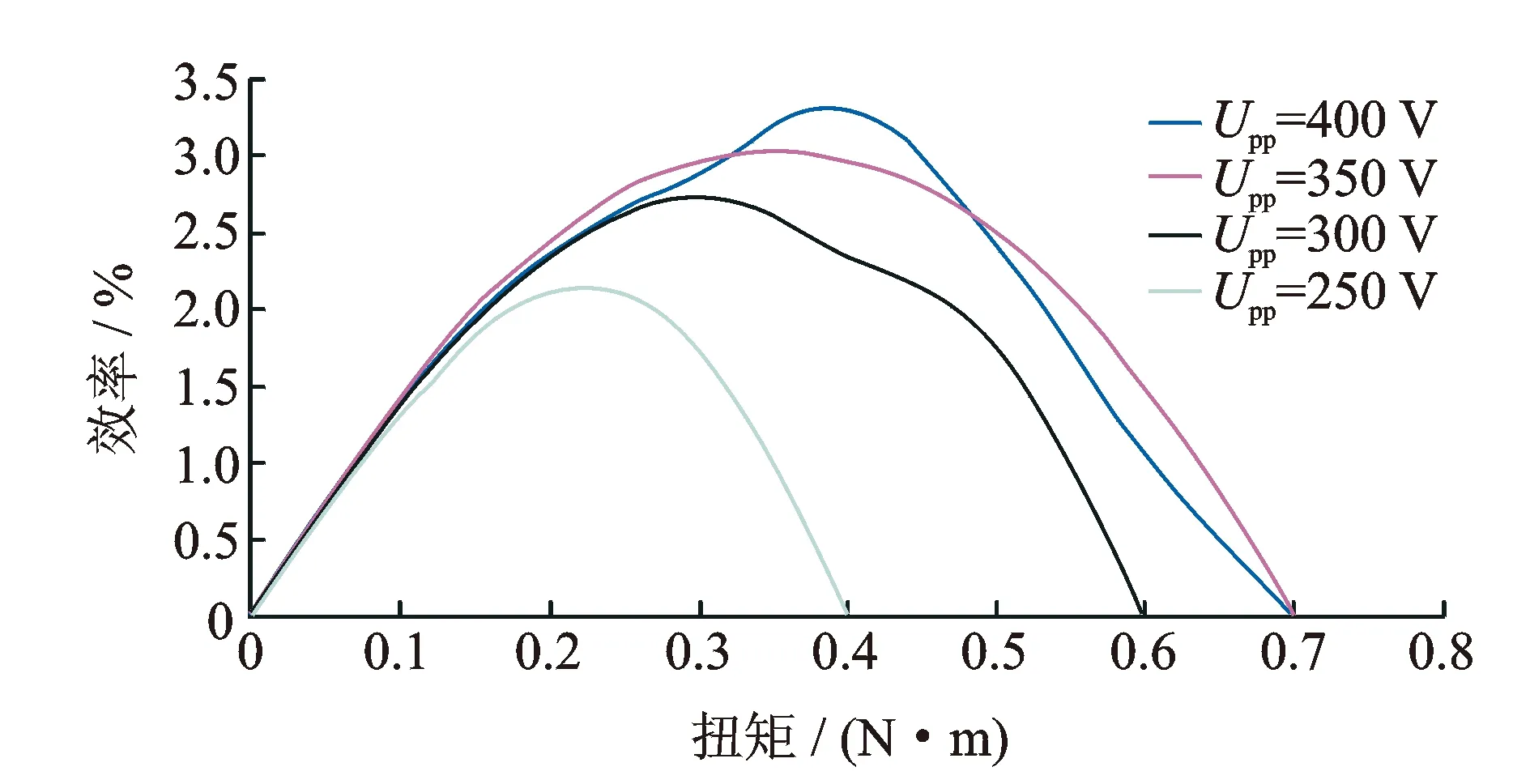
圖15 驅動電壓對系統效率的影響

由圖15可知，中空電機及其驅動系統總效率受到驅動電壓的影響較大，驅動電壓越大，電路總效率越高，電機輸出扭矩越大。驅動電壓往往受到壓電陶瓷片的耐壓閥值限制，不能太大。

4.3.3 諧振匹配點對系統效率的影響

根據參考文獻[16-17],行波超聲電機機電系統理想的匹配條件是匹配后電路的電納值為零。對于本研究的70中空超聲電機及其驅動系統，結合圖3可知電路匹配應滿足

(22)

筆者針對70中空電機及并聯電感匹配的驅動器做了諧振匹配點對系統效率的影響研究。其中變壓器副邊電感、壓電陶瓷片靜態電容為常量，Lp=576 μH，Ca=11 nF。

電機機械諧振頻率為39 500 Hz，分別匹配電容C1,代入式(22)可得到諧振電路的諧頻率,如表1所示。同時在驅動電壓峰-峰值為400 V、驅動頻率為40 200 Hz下分別測試3種系統的效率,可得到圖16所示曲線。

表1 匹配電容與諧振頻率

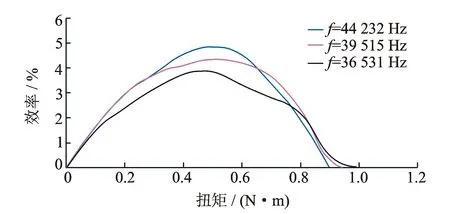
圖16 3種匹配點系統效率

由圖16可知,驅動電路匹配的諧振點遠遠高于電機機械諧振頻率，使得驅動信號頻率介于電路諧振頻率和機械諧振頻率之間時系統的效率最高。

5 結 論

1) 驅動頻率越靠近諧振頻率，電路總效率越高，電機輸出扭矩越大。

2) 驅動電壓越大，電路總效率越高，電機輸出扭矩越大。

3) 驅動電路匹配的諧振點遠遠高于電機機械諧振頻率，使得驅動信號頻率介于電路諧振頻率和機械諧振頻率之間時系統的效率最高。

[1] 周麗平，孫志峻，張泉，等．一種應用正態分布理論的直線超聲電機精密定位控制方法[J]．中國電機工程學報，2012，32(27)：60-65．

Zhou Liping， Sun Zhijun， Zhang Quan， et al． A precision alignment control method of linear ultrasonic motors using the normal distribution theory[J]． Proceedings of the CSEE，2012，32(27)：60-65． (in Chinese)

[2] 趙淳生．超聲電機技術與應用[M]．北京：科學出版社，2007：1-19．

[3] 趙淳生．世界超聲電機技術的新進展[J]．振動、測試與診斷，2004，24(1)：1-5．

Zhao Chunsheng． Recent propress in ultrasonic motor techniques[J]． Journal of Vibration， Measurement & Diagnosis，2004，24(1)：1-5. (in Chinese)

[4] 上羽貞行，富川義郎．超聲波馬達理論與應用[M]．上海：上海科學技術出版社，1998：55-58．

[5] 祖家奎，趙淳生．超聲電機定子的驅動方式及其振動響應特性[J].壓電與聲光，2006，28(1)：93-95．

Zu Jiakui， Zhao Chunsheng． Drive modes of stator of traveling wave ultrasonic motors and its vibration responses [J]． Piezoelect Rics & Acoustooptics，2006,28(1)：93-95． (in Chinese)

[6] 史敬灼，肖雋亞．超聲波電動機串聯電感匹配電路研究[J]．電機控制與保護，2008，27(12)：31-34．

Shi Jinzhuo， Xiao Juanya． The research of the ultrasonic motor series inductance matching circuit[J]． Motor Control and Protection，2008，27(12)：31-34． (in Chinese)

[7] 牛子杰，孫志峻，丁慶軍，等．定子完全固定的中空式超聲電機：中國，201320014338．3 [P]．2013-09-11．

[8] 梁大志，張軍，趙淳生，等．一種超聲電機雙PWM功率驅動拓撲結構：中國，201210451717.9 [P]．2012-11-13．

[9] 牛子杰，孫志峻，陳超，等．基于響應面模型與自適應遺傳算法的中空型行波超聲電機柔性轉子結構優化[J]．中國電機工程學報，2014，19(35)：62-64．

Niu Zijie， Sun Zhijun， Chen Chao, et al． Optimization of the rotor structure of a hollow traveling wave ultrasonic motor based on response surface methodology and self-adaptive genetic algorithm[J]． Proceedings of the CSEE，2014，19(35)：62-64. (in Chinese)

[10]李東旭．高等結構動力學[M]．長沙：國防科技大學出版社，1997:47-52.

[11]徐芝綸．彈性力學[M]．北京：高等教育出版社，1990:25-28.

[12]曹志遠．板殼振動理論[M]．北京：中國鐵道出版社，1989:34-36.

[13]Nesbitt W I, Andrew J. Modeling of a piezoelectric rotary ultrasonic motor[J]. IEEE Transactions Ultrasonics Ferroelectrics & Frequency Control, 1995,42(2):210-224.

[14]Jorg W. Contact mechanics of piezoelecctric ultrasonic motors[J]． Smart Materials and Structures, 1998(7):369-381.

[15]Zeng Jinsong， Chen Chao， Zhao Chunsheng. An effective technique for modifying modal frequencies of stator[C]∥The 2nd International Workshop on Piezoelectric Materials and Applications in Actuators. Paderborn,Germany: [s.n.],2005:456-466.

[16]林書玉.超聲換能器的原理及設計[M].北京：科學出版社，2004:35-38.

[17]陳永校，郭吉豐.超聲波電動機[M].杭州：浙江大學出版社，1994:22-25.

10.16450/j.cnki.issn.1004-6801.2015.06.002

*國家自然科學基金資助項目(51175264)；高校基本科研業務費科研基地創新基金資助項目(NJ20140026)

2014-11-25；

2014-12-28

TM359.4； TP273； TH113.1

牛子杰,男，1985年10月生，博士研究生。主要研究方向為行波超聲電機及其驅動控制系統。 E-mail：328920539@qq．com