芳綸/聚四氟乙烯纖維織物襯墊力學建模與性能計算

陳繼剛， 薛亞紅, 邱紅亮,3

(1. 燕山大學 機械工程學院， 河北 秦皇島 066004； 2. 燕山大學 國防重點學科實驗室， 河北 秦皇島 066004；3. 長治清華機械廠， 山西 長治 046000)

?

芳綸/聚四氟乙烯纖維織物襯墊力學建模與性能計算

陳繼剛1,2， 薛亞紅1,2, 邱紅亮1,2,3

(1. 燕山大學 機械工程學院， 河北 秦皇島 066004； 2. 燕山大學 國防重點學科實驗室， 河北 秦皇島 066004；3. 長治清華機械廠， 山西 長治 046000)

芳綸/聚四氟乙烯織物自潤滑襯墊是航空自潤滑關節軸承的功能件，在相關研究與分析的計算中，需要精確設置其材料的宏觀力學性能參數。為此，通過細觀構型計算獲得芳綸/聚四氟乙烯纖維織物宏觀力學性能參數。依據斜紋織物結構，給出了修正的RVE細觀模型，并建立了相應的彈性性能分析模型。應用數值模擬方法和解析法，分別計算了織物襯墊的力學性能參數，通過試驗數據比較，對模型與計算獲得的力學性能參數的有效性進行了驗證。結果表明，給出的參數化細觀結構模型可以用于織物襯墊力學性能計算，獲得宏觀的力學性能參數。

織物襯墊； 力學性能； 細觀建模； 數值計算； 自潤滑關節軸承

織物自潤滑襯墊是航空自潤滑關節軸承的重要功能件，其力學性能直接關系到軸承的應用及可靠性[1]。織物襯墊宏觀上屬于正交各向異性材料，在相關研究與計算中，依據不同的編織結構，常常需要設置其綜合力學性能的基礎數據，如果都應用物理試驗獲取這些參數，成本很高。研究結果表明，可以基于對織物構型數據、纖維束基礎數據，通過解析方法和數值模擬方法計算織物襯墊的力學性能參數[2]。現在對二維織物襯墊試驗的研究，大都局限在特定平紋結構，關于斜紋結構研究相對較少，缺乏通用性。文獻[3-4]提出的有限元法可以預測織物彈性性能，具有較好的精度。但是，關于自潤滑關節軸承自潤滑斜紋織物，目前還沒有能夠較全面地反映襯墊受拉壓變形與損傷，以及磨損的有限元彈性性能分析模型；在解析計算方面，劉召磊等[5]通過研究玻璃纖維和碳-50基體編織織物襯墊，在剛度平均基礎上結合結構幾何模型，提出了斜紋織物襯墊彈性性能計算的解析模型，但此模型與實際模型有一定差距。本文提出了一種修正模型，并且建立了參數化模型，用理論計算和數值模擬2種方法預測了自潤滑關節軸承斜紋襯墊力學性能，最后驗證了模型正確性，為自潤滑關節軸承研究的相關計算提供了襯墊力學性能參數。

1 織物襯墊細觀模型的提出

圖1為自潤滑斜紋織物細觀結構示意圖[6]。圖中所示襯墊經向纖維束由聚四氟乙烯(PTFE)纖維組成，緯向纖維束由芳綸纖維組成。基體將經向和緯向纖維固化在一起，使襯墊既能滿足強度要求，又能滿足自潤滑摩擦要求[7]。正常工況下，2個方向纖維相交處的相互擠壓和摩擦作用導致了纖維束截面向著接觸面積變大的方向發生變化。在顯微鏡下觀察織物截面，纖維束呈雙凸透鏡形(2個彎曲圓弧的對扣)[5]。

圖1 斜紋織物細觀結構示意圖Fig.1 Twill fabrics mesoscopic structure diagram

自潤滑織物襯墊編織結構呈現周期性，取其最小重復單元(圖1中虛線框部分)，即特征體積單元(RVE)來研究，RVE性能可反映其整體性能。基于文獻[1]，本文研究給出了其修正的細觀模型，考慮了2個纖維束之間的間隙，且間隙之間是一段與兩端圓弧相切的斜直線。圖2示出斜紋織物第1根經向紗線切分后的橫截面。 圖中bf、hf、rf分別為緯向纖維束寬度、厚度及截面圓弧半徑；Lsf、Lfg、Lfs分別為緯向纖維束節距、間隙及斜直線長度；θfc為半圓弧對應的圓心角；H為織物襯墊厚度；Lw為REV徑向長度。

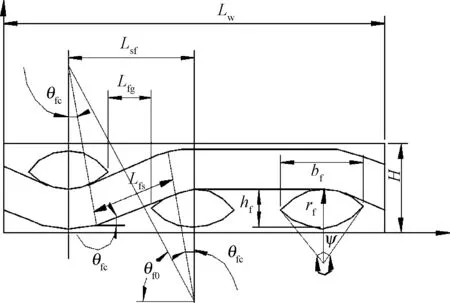
圖2 修正模型的RVE纖維束中間橫截面Fig.2 Intermediate cross section of REV fiber bundles of modification model

2 織物襯墊細觀模型的參數化建模

參數化建模思想是把模型中的幾何尺寸參數化，通過幾個特征基本變量來實現對模型的全約束，織物襯墊的基本參數為：b(纖維束寬度)、h(纖維束厚度)、H(織物襯墊厚度)、Ls(纖維束之間的間隙)。本文研究中，基于參數化CAD軟件，應用表達式與草圖約束工具，完成了參數化建模，圖3示出斜紋織物襯墊纖維束的參數化模型；圖4示出包括基體的整個RAE參數化模型。可以根據不同尺寸參數，來方便地自動生成織物襯墊三維幾何模型。

圖3 斜紋織物襯墊纖維束的參數化模型Fig.3 Twill fabric liner parameterized model of fiber bundles

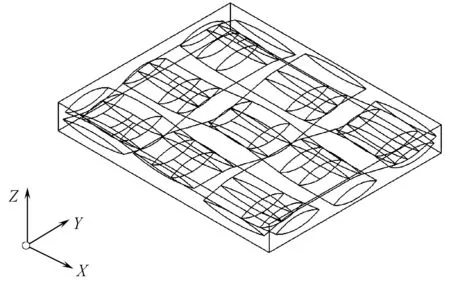
圖4 織物襯墊的樹脂模型與RVE三維模型Fig.4 Fabric liner resin model of RVE with 3-D model

3 織物襯墊有限元仿真

基于ANSYS系統，對織物襯墊RVE模型的彈性性能進行數值分析。分析選用Solid92單元。該單元具有二次位移型函數，能承受大變形，并且保持很高的計算精度[8-9]，對于不規則幾何模型非常適合，可以很好地劃分網格。表1示出芳綸/聚四氟乙烯纖維織物的幾何參數。采用Chamis模型計算得到纖維束彈性常數，從而代入有限元模型的材料屬性中。表2示出得到纖維束的細觀參數。其中：E11、E22表示X、Y方向的彈性模量；G12、G23表示剪切彈性模量；μ12、μ23表示對應泊松比。

表1 芳綸/聚四氟乙烯纖維織物的幾何參數

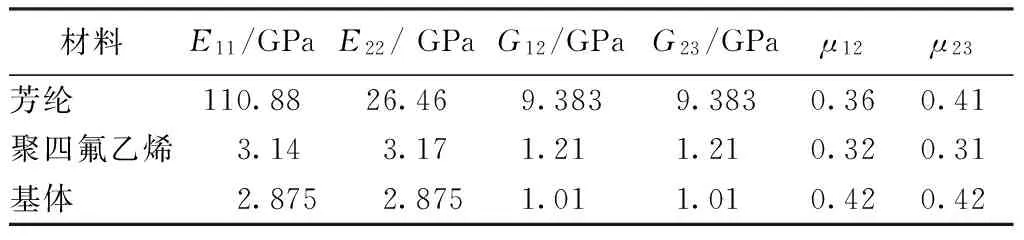
表2 芳綸/聚四氟乙烯纖維束的性能參數

織物襯墊屬于纖維復合材料，纖維束是單向(橫觀)同性材料，具有明顯的方向性，所以，在有限元模型中，根據纖維束走向確定單元坐標系，使單元坐標轉化到局部坐標系中。圖5(a)示出纖維束實際方向的坐標系，為了簡化模型設置圖5(b)局部坐標系。

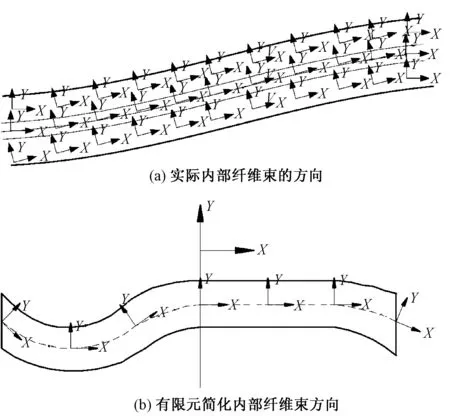
圖5 纖維束內部纖維方向定義Fig.5 Definition of fiber direction inside fiber bundle.(a) Actual fiber beam direction; (b) Finite element simplified fiber beam direction

3.1 拉伸彈性性能的有限元模擬

將有限元模型一側端面進行固定，對另一側端面所有節點進行耦合(保證拉伸時在同一平面內)，進行4組位移量L(2%、4%、6%、8%體積單元的長度LX)的拉伸、壓縮。圖6示出纖維束2個方向上的載荷形式簡圖。

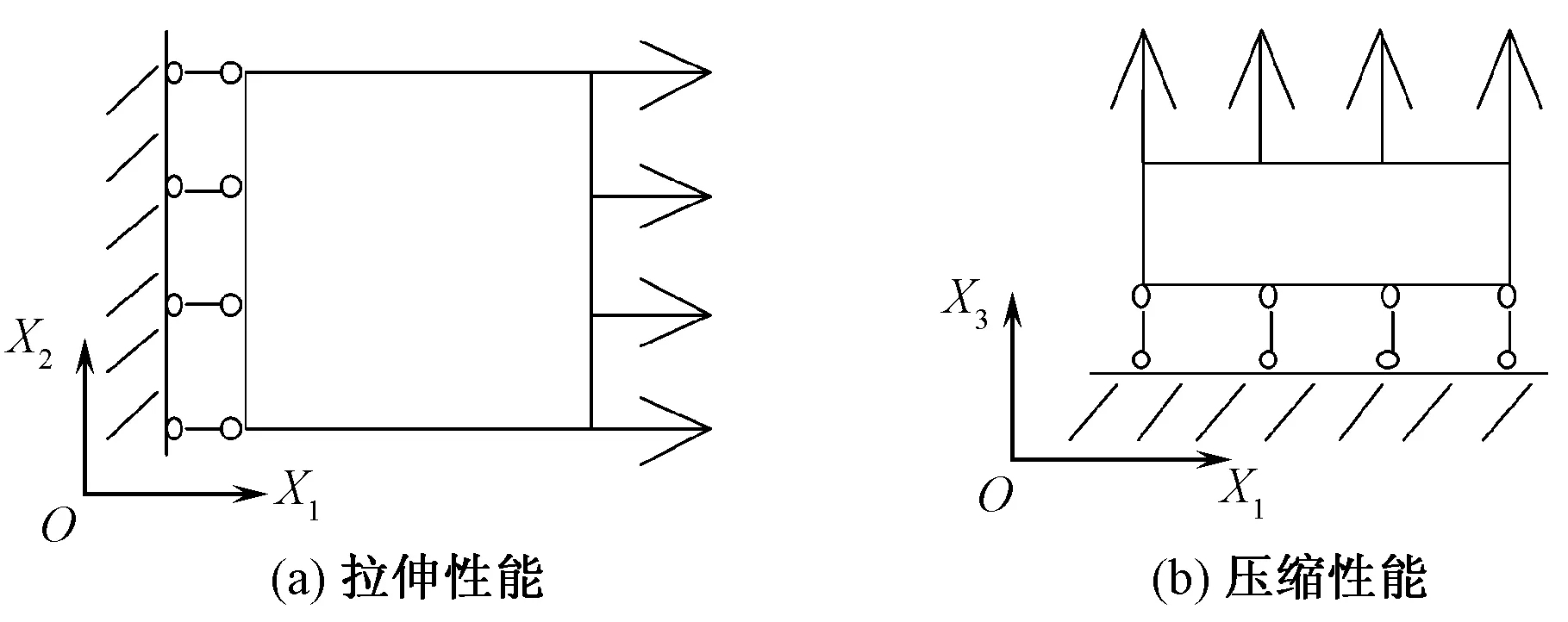
圖6 拉伸與壓縮性能加載示意圖Fig.6 Tensile(a) and compression (b) load performance diagram

受力面的等效拉伸應力是通過固定節點的支反力求面內積分得到，有應力平均法

(1)

式中S為應力的面積。

3.2 剪切模量有限元模擬

圖7示出計算剪切模量時的加載方式。

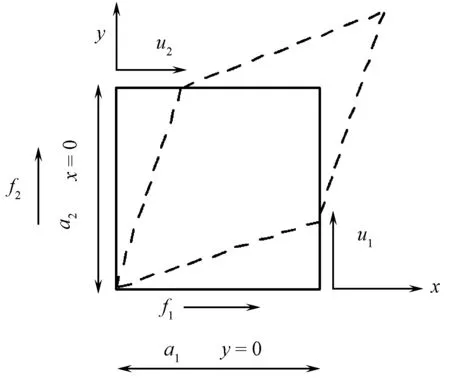
圖7 剪切性能加載示意圖Fig.7 Shear load performance diagram

在計算面內剪切模量時，如圖7所示施加載荷，把u1、u2作用在2個面上，則平均剪切應變為

(2)

平均剪切應力是在X面、Y面內節點合力f1、f2除以這2個面的面積。

(3)

由應力與應變之間的關系，可得彈性剪切模量，表3示出求得的織物性能參數。

表3 芳綸/聚四氟乙烯纖維織物性能

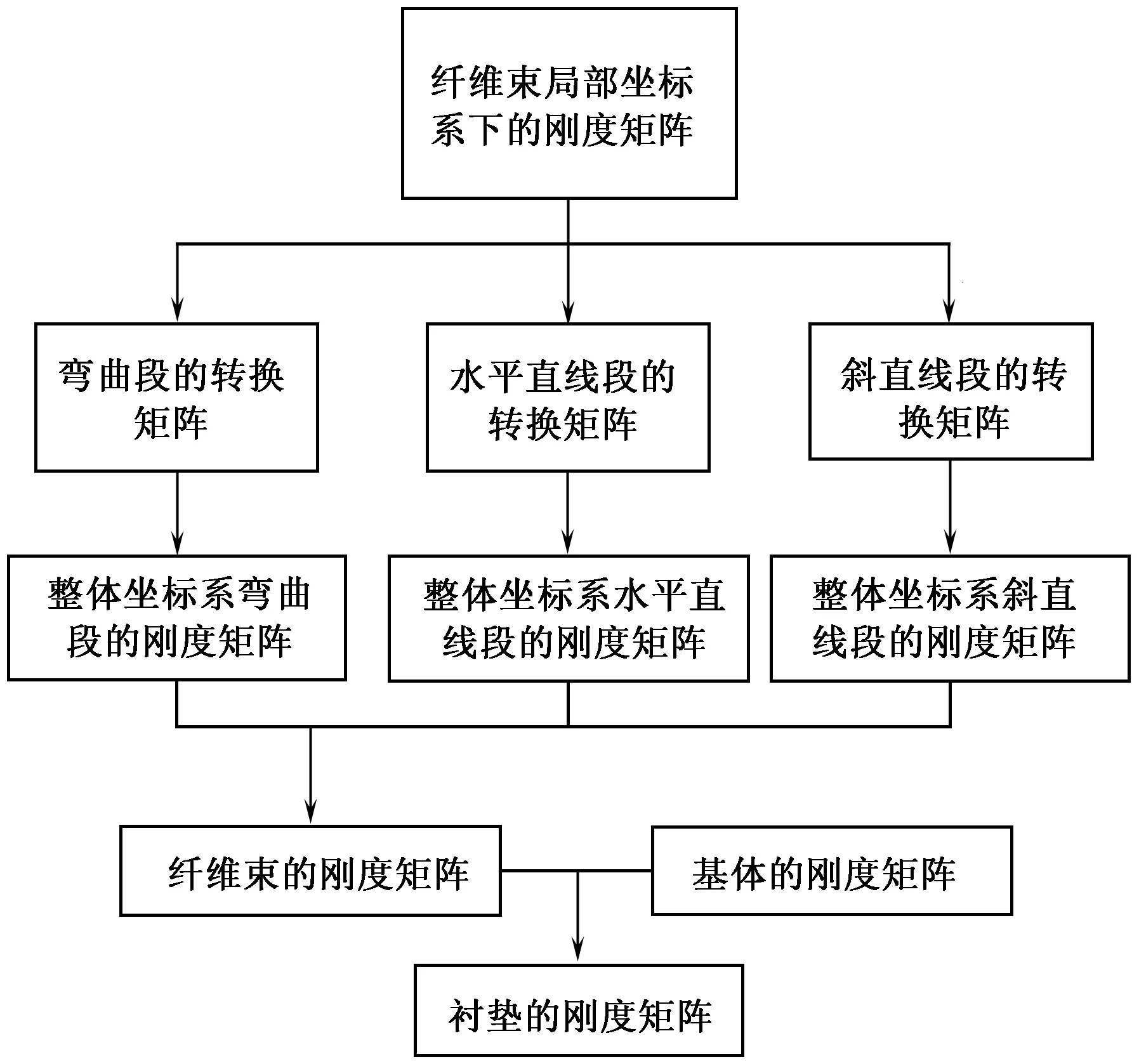
圖8 襯墊剛度的預測流程圖Fig.8 Liner stiffness prediction of flow chart

4 織物襯墊性能參數的解析計算

應用提出的細觀模型，通過纖維基體性質和纖維束中各組分比例，求出水平直線段、斜直線段和彎曲部分的剛度矩陣及橫縱纖維束在整個纖維束的比例，利用剛度平均法，計算整個襯墊的剛度矩陣，進而應用復合材料力學理論，解得襯墊各個方向上的彈性常數，襯墊剛度的預測流程如圖8所示。

4.1 纖維束性能參數計算

纖維束可以看成橫觀各向同性材料。實驗結果表明在計算纖維束性能參數時混合律公式仍然適用。可以應用纖維常數和基體常數，通過混合律計算，得出纖維束的性能參數，最為常用的是chamis模型。

(4)

式中：Ef1、Ef2分別為纖維方向和垂直纖維方向的彈性模量；Gf1、Gf2分別為纖維方向和垂直纖維方向的剪切模量；μf12、νf分別為纖維方向泊松比和紗線填充系數；Em、Gm、μm分別為基體彈性模量、 剪切模量和泊松比。

在局部坐標系下，橫觀各向同性材料的剛度矩陣為

(5)

其中k*=1-2v12v21(1+v23)-v232

纖維束的方向對襯墊的力學性質有很大影響，如果在襯墊中纖維某一部分是直線，則很容易用角度函數來表示，如果是曲線，可看成由無限個小斜直線段組成，斜直線段剛度矩陣可通過水平直線的剛度矩陣轉換得到。

(6)

纖維彎曲弧段可以看成是無數的微型直線段，則襯墊中彎曲纖維束的平均剛度矩陣Cij可用下式表示：

(7)

式中，θ為經緯向纖維束彎曲角。

應用經向和緯向彎曲部分的纖維束剛度矩陣，由彎曲部分、水平直線、斜直線部分在整個襯墊中的比例，利用式(8)可計算織物襯墊的等效剛度矩陣。

(8)

式中:λzw、λxw、λsw分別為水平直線段、圓弧段、斜直線段纖維的體積分數；Czw、Cxw、Csw分別為水平直線段、圓弧段、斜直線段纖維的剛度矩陣。

4.2 織物襯墊性能參數計算

基于前面的纖維束的等效剛度矩陣，再利用平均法，可以求得單胞模型的剛度矩陣。

(9)

式中:Cp、Cw、Cf、Cm分別指織物襯墊整體、經向纖維束、緯向纖維束和基體的剛度矩陣；λw、λf、λm分別為經向纖維束、緯向纖維束、基體的體積分數。

對式(9)求逆，便得到織物襯墊的柔度矩陣：

(10)

基于織物襯墊的柔度矩陣，根據織物襯墊的彈性常數與柔度矩陣中各向的關系，得到所需要的彈性常數。

(11)

根據文獻[7,10-11]，芳綸/聚四氟乙烯纖維織物襯墊的纖維性能數據見表4。

將表4中的數據代入有限元模型和解析模型，得到芳綸/聚四氟乙烯纖維織物性能參數，見表5。在通過數值分析方法研究自潤滑關節軸承的外形尺寸、制造過程和模擬各種工況時，這些性能參數可以為數值分析過程提供基礎材料性能數據。

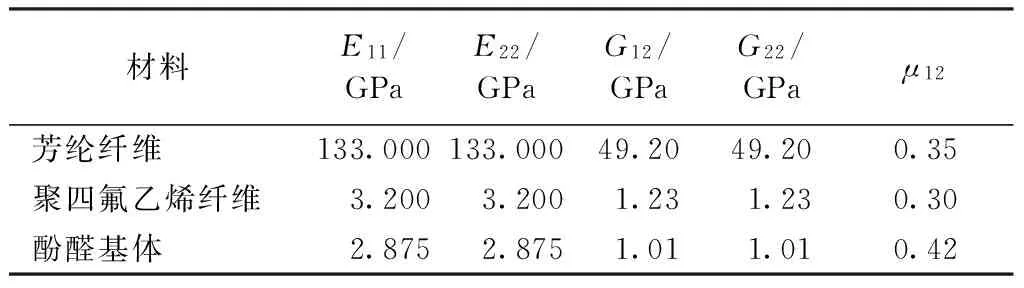
表4 芳綸、聚四氟乙烯、酚醛基體的性能參數

表5 芳綸/聚四氟乙烯纖維織物性能

5 織物襯墊性能測試實驗與驗證

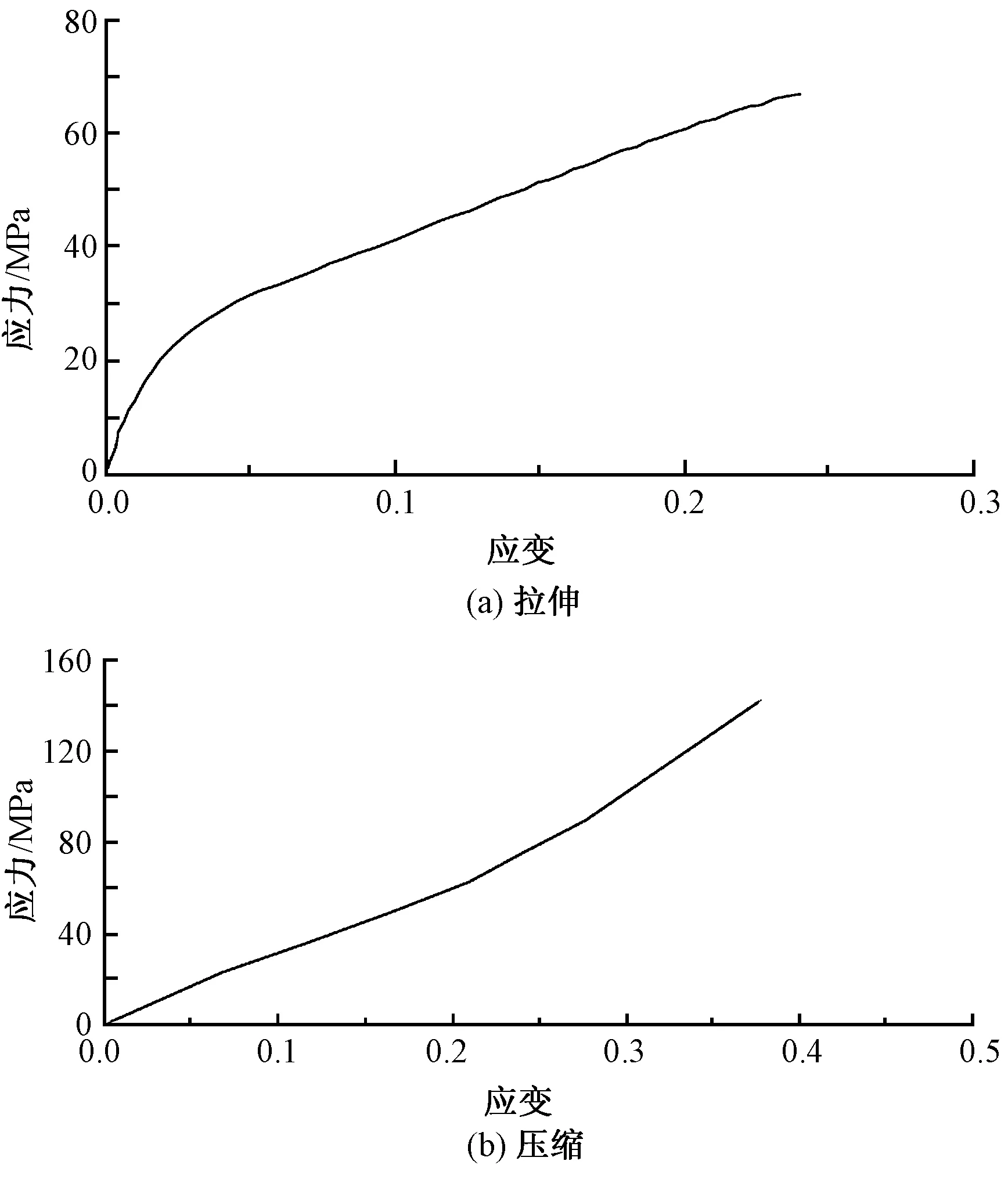
圖9 襯墊應力應變圖Fig.9 Liner stress-strain diagram.(a) Liner tensile; (b) Liner compression

為驗證上述計算獲得的力學性能參數的有效性，進行了織物襯墊的拉壓測試實驗。取有效寬度為50 mm，有效長度為100 mm的織物，在Y511B型電子織物強力機上以恒定的速度20 mm/min進行拉伸強度測試，記錄相應力與變形數據；在自制的試驗機上于織物襯墊的布面方向進行壓縮實驗，記錄壓縮力與變形數據。經數據處理，獲得織物襯墊纖維束方向的應力應變曲線和垂直纖維束方向的應力應變圖，見圖9。

依據實驗數據可獲得彈性模量，X方向為29.9 GPa，Y方向為9.50 GPa。與表3、5的數據進行比較，X方向的彈性模量解析值為30.207 GPa，有限元分析值為30.01 GPa；Y方向的彈性模量解析值為9.83 GPa，有限元分析值為9.811 GPa。可以看出基于細觀模型的計算值與實測值的偏差不大，說明提出的修正細觀模型在預測織物襯墊的力學性能參數方面有很好的吻合性。

6 結 論

[1] 楊育林, 祖大磊, 黃世軍. 自潤滑關節軸承現狀及發展[J].軸承, 2009(1): 58-61. YANG Yulin,ZU Dalei,HUANG Shijun. Status and development of self-lubricating spherical plain bearings[J]. Bearing, 2009(1): 58-61.

[2] 張文毅,姚振漢,姚學鋒,等. 編織復合材料的一種數值模型[J]. 工程力學, 2004(6): 56-60. ZHANG Wenyi, YAO Zhenhan, YAO Xuefeng, et al. A numerical model of woven fabric composites[J]. Engineering Mechanics, 2004(6): 56-60.

[3] BARBERO E J, TROVILLION J, MAYUGO J A,et al. Finite element modeling of plain weave fabrics from photomicrograph measurements [J]. Composite Structures, 2006,73(1): 41-52.

[4] CHAPHALKARP P, KELKAR A D. Analytical and experimental elastic behavior of twill woven laminate [C]//ICCM-12. Paris: Aviation Industry Press, 1999:41-43.

[5] 劉召磊,沈雪瑾. 自潤滑關節軸承斜紋織物襯墊彈性性能的分析模型[J]. 機械工程材料, 2011, 35(5): 96-100. LIU Zhaolei, SHEN Xuejin. Lubrication bearing liner elastic twill fabric performance analysis model[J]. Materials for Mechanical Engineering,2011, 35(5): 96-100.

[6] LI K W, SHEN X J, CHEN Y G, et al. Numerical analysis of woven fabric composites lubricated spherical plain bearings[C]//Proceedings of the XIth International Congress and Exposition. Shanghai: [s.n.], 2008: 2-5.

[7] 李如琰. 聚四氟乙烯纖維織物在關節軸承上的應用[J]. 功能材料, 2004(35): 2221-2223. LI Ruyan. The application of poly tetra fluoro ethylene fabrics to spherical plain bearings[J].Functional Materials,2004(35): 2221-2223.

[8] 張朝暉. ANSYS 12.0結構分析工程應用實例解析[M]. 北京:機械工業出版社, 2010: 400-450. ZHANG Chaohui. Structure Analysis of the Engineering Application Examples by ANSYS 12.0[M]. Beijing: China Machine Press,2010: 400-450.

[9] 王新敏,李義強,許宏偉.Ansys結構分析單元與應用[M].北京：人民交通出版社,2011:200. WANG Xinmin, LI Yiqiang, XU Hongwei. ANSYS of Structural Analysis Unit and Application[M]. Beijing: People Transport Press,2011:200.

[10] 溫建萍, 曾敏, 甄明輝, 等. TC4-PTFE復合材料的結構設計與摩擦磨損性能[J]. 中國機械工程, 2005(11): 2064-2067. WEN Jianping, ZENG Min, ZHEN Minghui, et al. Structure design and tribological properties for TC4-PTFE composites [J]. China Mechanical Engineering, 2005(11): 2064-2067.

[11] 周玉璽, 曾金芳, 王斌. 芳綸與Kevlar-49纖維組成結構與力學性能的對比[J]. 宇航材料工藝, 2007(3): 71-73. ZHOU Yuxi, ZENG Jinfang, WANG Bin. Comparision of aramid: Ⅲ: fibre′s component, structure and mechanical properties with Kevlar-49 fibre[J]. Aerospace Materials & Technology, 2007(3): 71-73.

Mechanics modeling and performance calculation of aramid/polytetrafluoroethene fabric liner

CHEN Jigang1,2, XUE Yahong1,2, QIU Hongliang1,2,3

(1.SchoolofMechanicalEngineering,YanshanUniversity,Qinhuangdao,Hebei066004,China； 2.KeyLaboratoryofFundamentalScienceforNationalDefence,YanshanUniversity,Qinhuangdao,Hebei066004,China；3.ChangzhiQinghuaMachineryFactory,Changzhi,Shanxi046000,China)

Aramid/polytetrafluoroethene fabric self-lubricating liner is one of function parts of self-lubricating spherical plain bearing, and its macroscopic mechanical properties parameters should be set up accurately in the calculation of relevant research and analysis. The research purpose is to acquire macro mechanics performance parameters of the aramid/ polytetrafluoroethene fabric by the calculation of mesoscopic configuration. Based on the twill structure, the fixed RVE mesoscopic model and elastic performance analysis model had been built. The mechanics properties parameters had been calculated by numerical simulation method and analytic method. And then, comparing with experimental data, the effectiveness of the given model and the mechanics performance parameters had been verified. The study shows that the given parameterized mesoscopic structure model can be used to calculate the macro mechanical performances. Thus, the fabric liner mechanics performance can be achieved accurately.

fabric liner; mechanical property; mesoscopic model; numerical calculation; self-lubricating spherical plain bearing

10.13475/j.fzxb.201501008206

2013-11-18

2014-05-26

國防基礎重大項目(JPPT-ZCGX-*)

陳繼剛(1970—)，男，副教授。研究方向為自潤滑材料、精密成形、航空軸承技術等。E-mail：24000082@qq.com。

TH 161

A