雙樹(shù)復(fù)小波包和ICA用于滾動(dòng)軸承復(fù)合故障診斷*

胥永剛, 孟志鵬, 陸 明

(北京工業(yè)大學(xué)北京市精密測(cè)控技術(shù)與儀器工程技術(shù)研究中心 北京， 100124)

雙樹(shù)復(fù)小波包和ICA用于滾動(dòng)軸承復(fù)合故障診斷*

胥永剛, 孟志鵬, 陸 明

(北京工業(yè)大學(xué)北京市精密測(cè)控技術(shù)與儀器工程技術(shù)研究中心 北京， 100124)

針對(duì)滾動(dòng)軸承復(fù)合故障信號(hào)特征難以分離的問(wèn)題，提出將雙樹(shù)復(fù)小波包變換和獨(dú)立分量分析(independent component analysis，簡(jiǎn)稱ICA)結(jié)合的方法應(yīng)用到滾動(dòng)軸承復(fù)合故障診斷中。首先，利用雙樹(shù)復(fù)小波包變換將復(fù)雜的、非平穩(wěn)的復(fù)合故障信號(hào)分解為若干不同頻帶的分量；其次，引入ICA對(duì)各個(gè)分量所組成的混合信號(hào)進(jìn)行盲源分離，從而盡可能消除頻率混疊；最后，對(duì)從混合信號(hào)中分離出來(lái)的獨(dú)立信號(hào)分量進(jìn)行希爾伯特解調(diào)，即可實(shí)現(xiàn)對(duì)復(fù)合故障特征信息的分離和故障識(shí)別。試驗(yàn)結(jié)果表明，該方法可以有效地分離和提取軸承復(fù)合故障的特征頻率，驗(yàn)證了方法的可行性和有效性。

雙樹(shù)復(fù)小波包變換； 獨(dú)立分量分析； 盲源分離； 頻率混疊； 復(fù)合故障

引 言

滾動(dòng)軸承作為旋轉(zhuǎn)機(jī)械最關(guān)鍵的零部件之一，其運(yùn)行狀態(tài)直接影響到整臺(tái)機(jī)器的精度、可靠性及壽命等。滾動(dòng)軸承故障是導(dǎo)致機(jī)械設(shè)備運(yùn)行過(guò)程中產(chǎn)生故障的主要原因之一,對(duì)滾動(dòng)軸承故障診斷技術(shù)進(jìn)行研究具有十分重要的意義。目前，滾動(dòng)軸承故障診斷方法大多只對(duì)單一故障進(jìn)行了相關(guān)研究，而在實(shí)際工程應(yīng)用中，故障往往不是單獨(dú)出現(xiàn)的，而是同時(shí)發(fā)生幾種故障形成復(fù)合故障。當(dāng)機(jī)械設(shè)備出現(xiàn)復(fù)合故障時(shí)，針對(duì)非平穩(wěn)的并且故障源數(shù)未知的混合信號(hào)，有效地從混合信號(hào)中分離出單一故障信號(hào)對(duì)于準(zhǔn)確判斷軸承故障十分重要。

雙樹(shù)復(fù)小波變換(dual-tree complex wavelet transform,簡(jiǎn)稱 DTCWT)[1-2]是近幾年發(fā)展起來(lái)的一種具有諸多優(yōu)良特性的新型小波變換方法，具有近似平移不變性、良好的方向選擇性、完全重構(gòu)性、有限的數(shù)據(jù)冗余性和高效的計(jì)算效率等優(yōu)良性質(zhì)。但是雙樹(shù)復(fù)小波變換同傳統(tǒng)小波變換一樣，對(duì)高頻部分沒(méi)有繼續(xù)進(jìn)行細(xì)分。故提出雙樹(shù)復(fù)小波包變換[3]，對(duì)雙樹(shù)復(fù)小波變換中沒(méi)有細(xì)分的高頻部分作進(jìn)一步的分解，從而提高信號(hào)整個(gè)頻段的頻率分辨率，減少信息的丟失。目前，雙樹(shù)復(fù)小波包變換在圖像處理[4]、語(yǔ)音處理[5]和故障診斷[6-7]等領(lǐng)域已有相關(guān)應(yīng)用。

獨(dú)立分量分析(ICA)是盲源分離的一種特殊方法[8-9],其處理的對(duì)象是相互統(tǒng)計(jì)獨(dú)立的信號(hào)源經(jīng)線性組合而產(chǎn)生的一組混合信號(hào),最終目的是從混合信號(hào)中分離出各自獨(dú)立的信號(hào)分量。ICA在機(jī)械故障診斷、通信技術(shù)、生物醫(yī)學(xué)等領(lǐng)域都有廣泛的運(yùn)用[8-11]。

雙樹(shù)復(fù)小波包變換相對(duì)傳統(tǒng)離散小波包變換，頻率混疊現(xiàn)象得到明顯的抑制，但是仍然存在微小的頻率混疊。筆者提出了基于雙樹(shù)復(fù)小波包變換和ICA的故障診斷方法，利用ICA消除雙樹(shù)復(fù)小波包變換的頻率混疊問(wèn)題，并將其應(yīng)用于滾動(dòng)軸承復(fù)合故障診斷中。試驗(yàn)結(jié)果表明，該方法可以有效地分離和提取滾動(dòng)軸承復(fù)合故障的特征頻率。

1 雙樹(shù)復(fù)小波包變換

雙樹(shù)復(fù)小波變換具有諸多優(yōu)良的特性，但是同傳統(tǒng)離散小波變換一樣，對(duì)高頻部分沒(méi)有進(jìn)行進(jìn)一步細(xì)分。

傳統(tǒng)的離散小波包變換(discrete wavelet packet transform ,簡(jiǎn)稱DWPT)在分解時(shí)，由于每次分解都采用下抽樣操作，這樣使每次分解后信號(hào)的采樣頻率降低一半，時(shí)間分辨率也降低一半。所以一旦分解層數(shù)確定，頻帶的頻率分辨率也就確定，分解的層數(shù)越多，頻率分辨率越高，但是時(shí)間分辨率越低。同時(shí)，下抽樣的操作不具有平移不變性，還會(huì)引起較大的頻率混疊問(wèn)題。此外，對(duì)信號(hào)的奇異點(diǎn)敏感，難以有效地提取信號(hào)的特征頻率[7]。

針對(duì)傳統(tǒng)小波包變換的缺陷和雙樹(shù)復(fù)小波變換的優(yōu)良特性和不足之處，提出雙樹(shù)復(fù)小波包變換(dual-tree complex wavelet packet transform, 簡(jiǎn)稱DT-CWPT)[3]。

雙樹(shù)復(fù)小波包變換的分解和重構(gòu)實(shí)現(xiàn)非常簡(jiǎn)單，它由兩個(gè)平行且使用不同的低通和高通濾波器的離散小波包變換構(gòu)成，其兩層分解和重構(gòu)過(guò)程如圖1所示。兩個(gè)并行離散小波包變換，一個(gè)離散小波包變換可以看做實(shí)樹(shù)，另一個(gè)小波包變換看做虛樹(shù)，在信號(hào)的分解過(guò)程中可以形成互補(bǔ)，也能獲得近似平移不變性。對(duì)雙樹(shù)復(fù)小波分解沒(méi)有細(xì)分的高頻部分也進(jìn)行了分解，減少了信息的丟失。其中第1層分解，經(jīng)過(guò)first_1濾波器組的為實(shí)樹(shù)小波包分解。first_1濾波器有兩行，第1行f1-0為低通濾波器，第1行f1-1為高通濾波器。經(jīng)過(guò)first_2濾波器組的是虛部小波包分解。對(duì)于第2層以上的分解，為了保證兩樹(shù)在該層和所有前層上產(chǎn)生的延遲差的總和相對(duì)于原信號(hào)輸入為一個(gè)采樣周期，即兩樹(shù)對(duì)應(yīng)濾波器的相頻響應(yīng)之間應(yīng)有半個(gè)采樣周期的群延遲, 且兩濾波器的幅頻響應(yīng)相等，實(shí)樹(shù)小波包分解交替使用Q_shift濾波器組h，同樣虛部樹(shù)分解交替使用Q_shift濾波器組g。在各層分解過(guò)程中采用了系數(shù)二分去除了多余的計(jì)算，提高了信號(hào)處理效率。雙樹(shù)復(fù)小波包變換的重構(gòu)過(guò)程為分解的逆過(guò)程[3,6-7]。

圖1 雙樹(shù)復(fù)小波包變換的分解和重構(gòu)過(guò)程Fig.1 Decomposition and reconstruction process using dual-tree complex wavelet packet transform

同傳統(tǒng)的離散小波包變換一樣，由于在分解過(guò)程中隔點(diǎn)采樣導(dǎo)致采樣頻率減半，而高頻部分不滿足采樣定理而發(fā)生頻率折疊，對(duì)高頻部分繼續(xù)分解就會(huì)產(chǎn)生頻帶交錯(cuò)。雙樹(shù)復(fù)小波包變換利用兩樹(shù)的信息互補(bǔ)，在一定程度抑制了頻率混疊的程度，但還是存在微小的頻率混疊的問(wèn)題。

2 獨(dú)立分量分析

獨(dú)立分量分析的實(shí)質(zhì)是在統(tǒng)計(jì)獨(dú)立性的假設(shè)下，對(duì)多路觀測(cè)信號(hào)進(jìn)行盲分離，挖掘出隱含在觀測(cè)信號(hào)中的獨(dú)立源成分。

設(shè)N個(gè)觀測(cè)信號(hào)X=[x1,x2,…,xN]T是由M個(gè)獨(dú)立的信號(hào)源S=[s1,s2,…,sM]T的線性混合

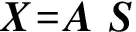
(1)

其中：A為N×M的未知混合矩陣。

盲源分離通過(guò)從觀測(cè)信號(hào)中恢復(fù)出源信號(hào)矢量，即要找到一個(gè)分離矩陣W從混合信號(hào)中分離出相互獨(dú)立的源信號(hào)，即

(2)

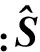
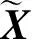
1) 對(duì)混合信號(hào)去除均值并白化處理；

2) 隨機(jī)選擇具有單位方差的初始分離矩陣W；

5) 如果分離矩陣收斂, 則迭代逼近過(guò)程結(jié)束, 否則返回步驟3。

得到分離矩陣W后，很容易求出源信號(hào)的估計(jì)

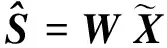
(3)

3 仿真分析

本方法的算法流程如圖2所示。首先，利用DT-CWPT將原始信號(hào)分解為不同頻帶的分量；然后，由于分解后的分量存在一定的頻率混疊，故將分解后不同分量和原始信號(hào)作為混合信號(hào)利用FastICA進(jìn)行盲源分離得到各個(gè)獨(dú)立的信號(hào)分量；最后，利用希爾伯特包絡(luò)解調(diào)，即可有效地分離故障特征頻率。

圖2 基于DT-CWPT和ICA的診斷方法
Fig.2 The diagnosis method based on DT-CWPT and ICA

為了揭示雙樹(shù)復(fù)小波包變換在抑制頻率混疊方面較傳統(tǒng)離散小波包變換的優(yōu)越性，構(gòu)造如下信號(hào)

(4)

其中：x1(t)=sin(110πt)；x2(t)=sin(260πt)；

x3(t)=sin(580πt)；x4(t)=sin(640πt)。

該仿真信號(hào)的采樣頻率為800 Hz,采樣點(diǎn)數(shù)為512點(diǎn)，分別進(jìn)行2層分解。圖3為傳統(tǒng)離散小波包分解(db3小波)的波形及頻譜，可以看出頻率混疊較為嚴(yán)重，同時(shí)出現(xiàn)了70，270 Hz等虛假頻率。圖4為雙樹(shù)復(fù)小波包分解的波形及頻譜，與圖3相比較，頻率混疊現(xiàn)象得到明顯抑制，但仍然存在一定的頻率混疊問(wèn)題。

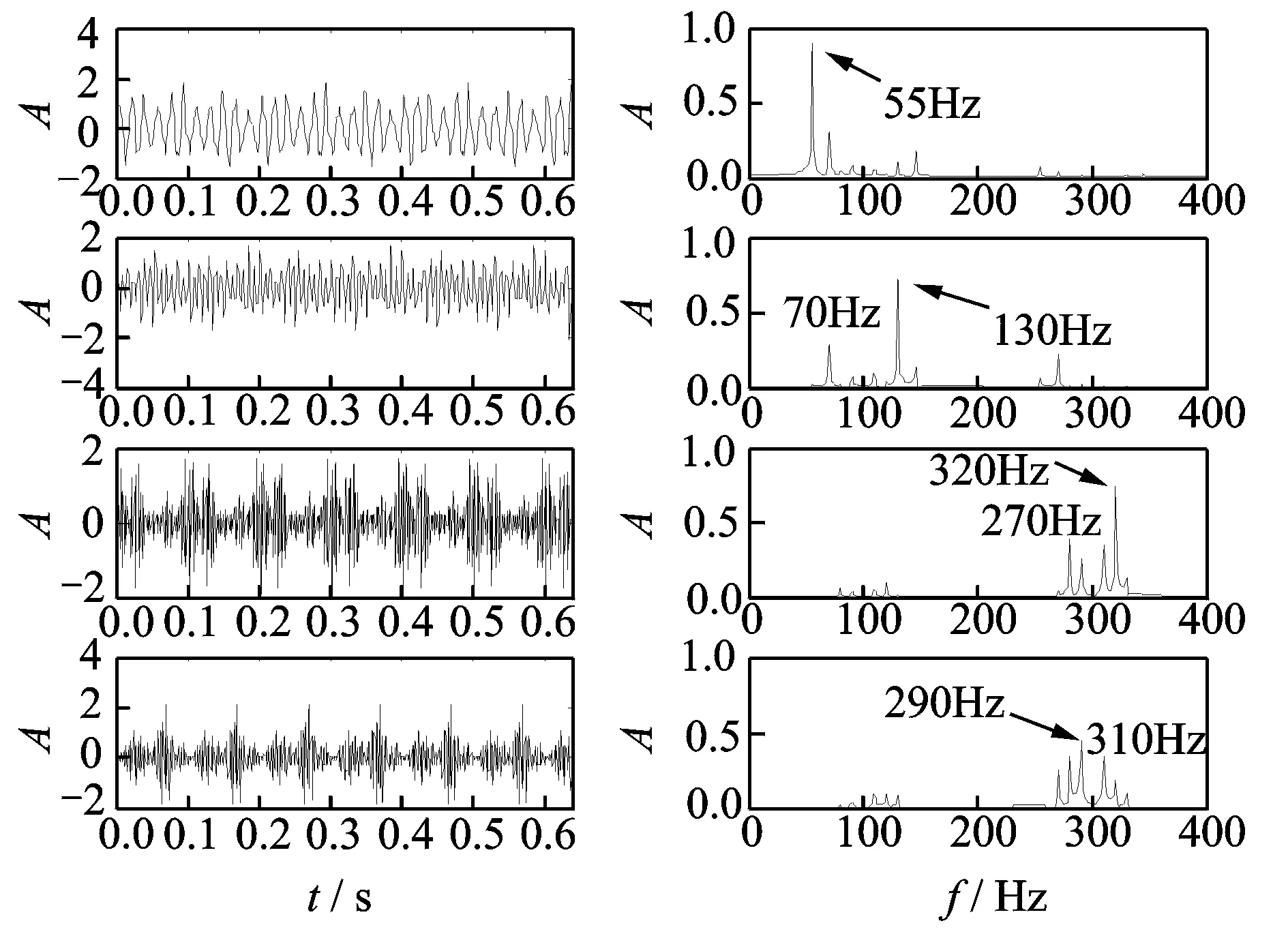
圖3 2層傳統(tǒng)離散小波包分解后的波形及頻譜Fig.3 Waveforms and spectrums of 2 level CWPT decomposition

將雙樹(shù)復(fù)小波包分解后的4個(gè)分量和原始信號(hào)作為混合信號(hào)，利用FastICA進(jìn)行盲源分離，得到的獨(dú)立分量的波形及其頻譜如圖5所示。從盲源分離后的各個(gè)獨(dú)立分量的波形和頻譜圖中可以看出，波形的周期性和光滑性更為理想，頻率成分更為獨(dú)立，已基本消除了頻率混疊的現(xiàn)象。

圖4 2層雙樹(shù)復(fù)小波包分解后的波形及頻譜Fig.4 Waveforms and spectrums of 2 level DT-CWPT decomposition

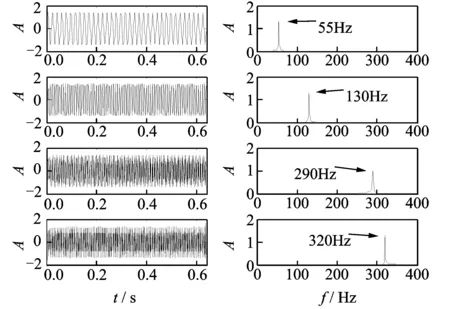
圖5 FastICA 處理后波形及頻譜Fig.5 Waveforms and spectrums of ICA

4 試驗(yàn)分析

滾動(dòng)軸承故障模擬試驗(yàn)系統(tǒng)如圖6所示，試驗(yàn)系統(tǒng)由軸承試驗(yàn)臺(tái)、壓電式加速度傳感器、數(shù)據(jù)采集儀、筆記本電腦組成。將正常和有故障軸承依次安裝在軸承試驗(yàn)臺(tái)上，進(jìn)行試驗(yàn)數(shù)據(jù)的采集，數(shù)據(jù)采集儀將采集數(shù)據(jù)傳到電腦中，進(jìn)行數(shù)據(jù)處理分析。

圖6 滾動(dòng)軸承故障模擬試驗(yàn)系統(tǒng)Fig.6 Bearing fault simulate experiment system

該試驗(yàn)的滾動(dòng)軸承型號(hào)為6307，電機(jī)轉(zhuǎn)速為1 496r/min，采樣頻率為15 360 Hz，模擬了試驗(yàn)臺(tái)末端軸承外圈裂紋和內(nèi)圈裂紋的復(fù)合故障，以及軸承外圈裂紋和滾動(dòng)體點(diǎn)蝕的復(fù)合故障試驗(yàn)。其中，內(nèi)外圈裂紋故障是利用線切割技術(shù)分別在軸承內(nèi)圈和外圈加工了一條寬為0.5 mm、深為0.5 mm的槽來(lái)模擬。滾動(dòng)體點(diǎn)蝕故障是采用電火花加工技術(shù)在軸承滾動(dòng)體上加工了1個(gè)直徑2 mm、深0.1 mm的小凹坑來(lái)模擬。

在滾動(dòng)軸承運(yùn)行過(guò)程中，一旦軸承部件出現(xiàn)裂紋、點(diǎn)蝕等缺陷，會(huì)產(chǎn)生沖擊性振動(dòng)，其振動(dòng)頻率即為軸承各部件的特征頻率。在滾動(dòng)軸承故障診斷過(guò)程中，利用信號(hào)處理方法檢測(cè)出軸承零部件的特征頻率，即可判斷該零部件已產(chǎn)生故障。

經(jīng)查詢機(jī)械手冊(cè)，6307軸承的滾動(dòng)體直徑d=13.64 mm，軸承節(jié)徑D=57.5 mm，滾動(dòng)體個(gè)數(shù)z=8，接觸角α=0°，同時(shí)軸承內(nèi)圈旋轉(zhuǎn)頻率fr=1 496/60=24.933 Hz，則外圈的特征為

(5)

內(nèi)圈的特征頻率為

(6)

滾動(dòng)體的特征頻率為

(7)

圖7為滾動(dòng)軸承同時(shí)存在內(nèi)圈裂紋和外圈裂紋復(fù)合故障的原始時(shí)域波形及幅值譜，從波形和幅值譜中基本看不出故障特征信息，同時(shí)有明顯的干擾成分。利用DT-CWPT對(duì)原始信號(hào)進(jìn)行3層分解，得到8個(gè)頻帶分量a31～a38的波形如圖8所示。

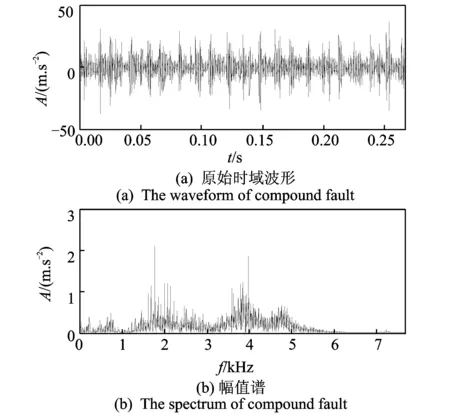
圖7 內(nèi)外圈裂紋復(fù)合故障波形和頻譜Fig.7 Waveform and spectrum of inner and outer crack compound fault

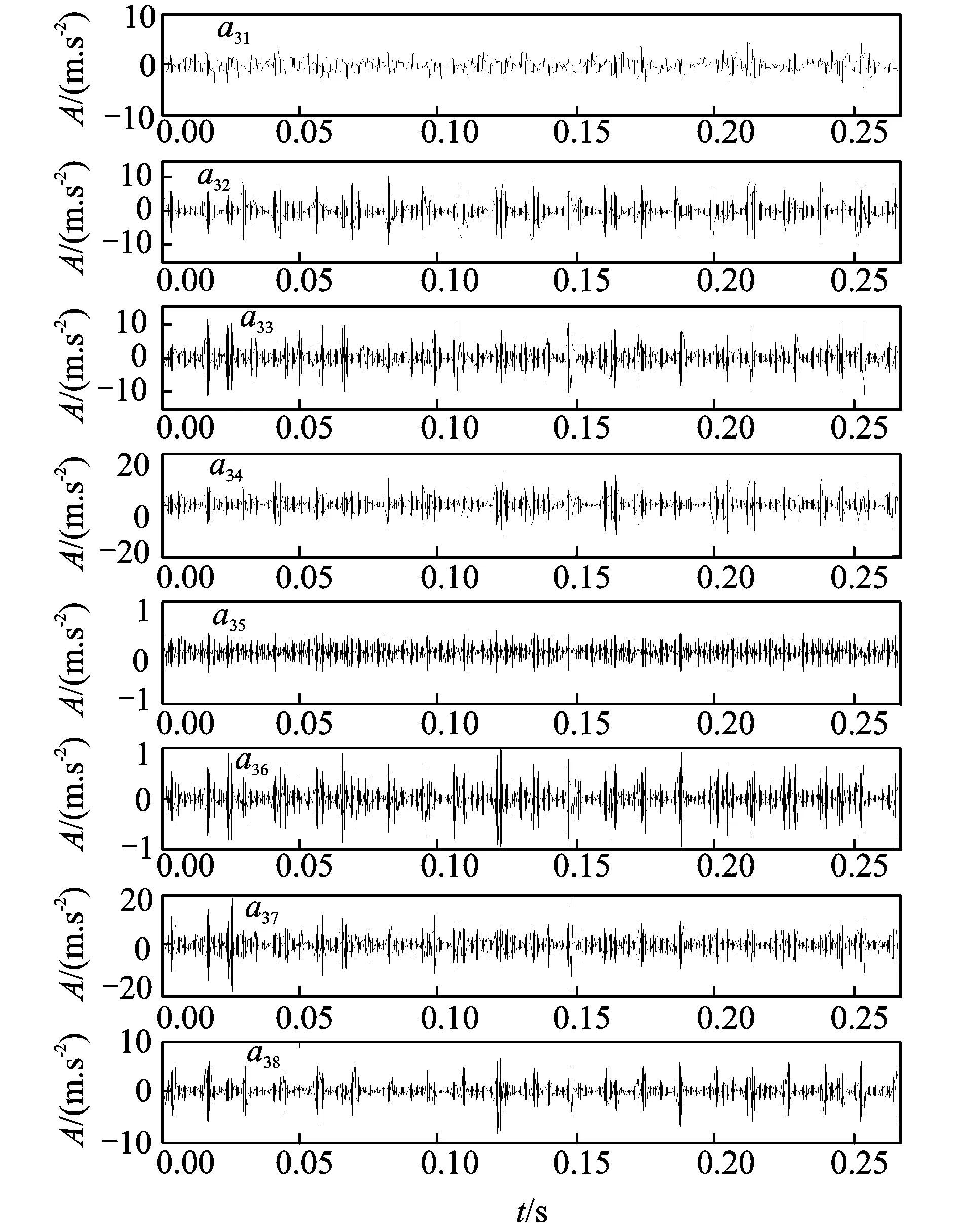
圖8 雙樹(shù)復(fù)小波包分解結(jié)果Fig.8 Waveforms of DT-CWPT decomposition

將雙樹(shù)復(fù)小波包分解后的分量a32，a33，a34，a36，a37，a38以及原始信號(hào)作為混合信號(hào)(a31，a35明顯為干擾成分，故去除)，利用FastICA進(jìn)行盲源分離去除頻率混疊得到各個(gè)獨(dú)立的分量。圖9所示為包含故障特征的兩個(gè)獨(dú)立分量的波形及其對(duì)應(yīng)的希爾伯特包絡(luò)解調(diào)譜。由圖(b)中可以清楚地看到123.8，243.8，367.5 Hz的頻率成分，與軸承內(nèi)圈的特征頻率122.738 Hz及其倍頻非常接近，故可判斷該軸承內(nèi)圈存在故障。同樣由圖(d)中可以清楚地看到75，153.8，228.8 Hz…等頻率成分，與軸承外圈的特征頻率76.728 Hz及其倍頻非常接近，故可判斷該軸承外圈存在故障。

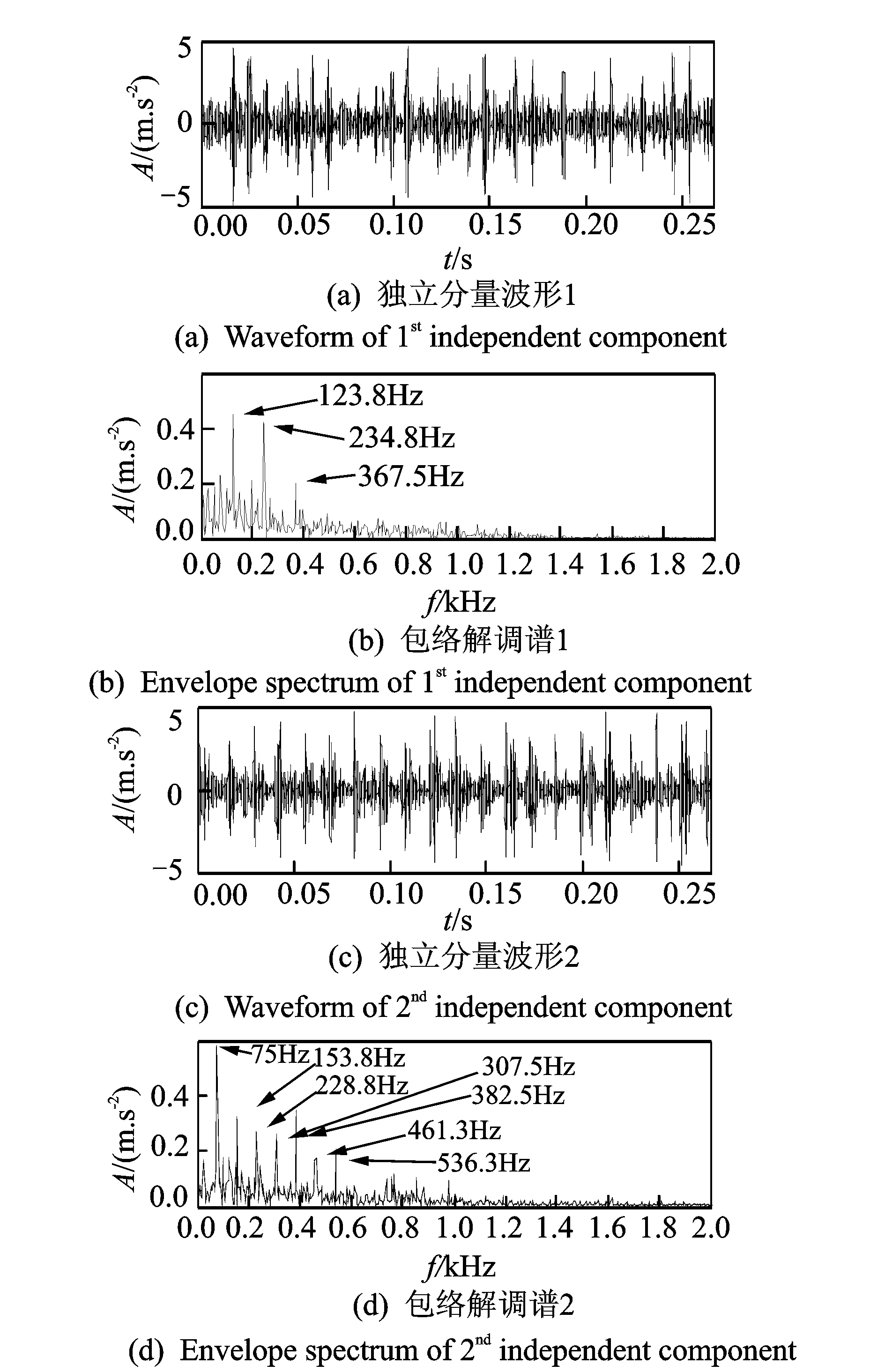
圖9 內(nèi)外圈復(fù)合故障FastICA分離后的波形及包絡(luò)解調(diào)譜Fig.9 Waveform and envelope spectrums of inner and outer compound fault after FastICA

圖10為軸承外圈裂紋和滾動(dòng)體點(diǎn)蝕復(fù)合故障的信號(hào)時(shí)域波形和頻譜。同樣利用本方法進(jìn)行分析，得到處理后的結(jié)果如圖11所示。由圖(b)中可以清楚地看到75 Hz的頻率成分，與軸承外圈的特征頻率76.728 Hz非常接近，故可判斷該軸承外圈存在故障。同樣由圖(d)中可以清楚地看到52.5和105 Hz的頻率成分，與軸承滾動(dòng)體的特征頻率51.171 Hz及其二倍頻非常接近，故可判斷該軸承滾動(dòng)體存在故障，這與試驗(yàn)?zāi)M外圈裂紋和滾動(dòng)體點(diǎn)蝕復(fù)合故障事實(shí)相符。上述結(jié)果表明，本研究方法可以有效地分離和提取滾動(dòng)軸承復(fù)合故障的特征信息。

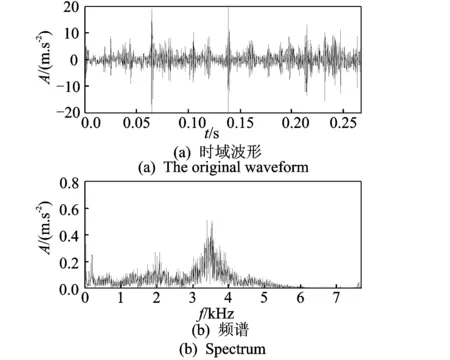
圖10 外圈裂紋和滾動(dòng)體點(diǎn)蝕復(fù)合故障波形和頻譜Fig.10 Waveform and spectrum of outer crack and rolling element pitting compound fault

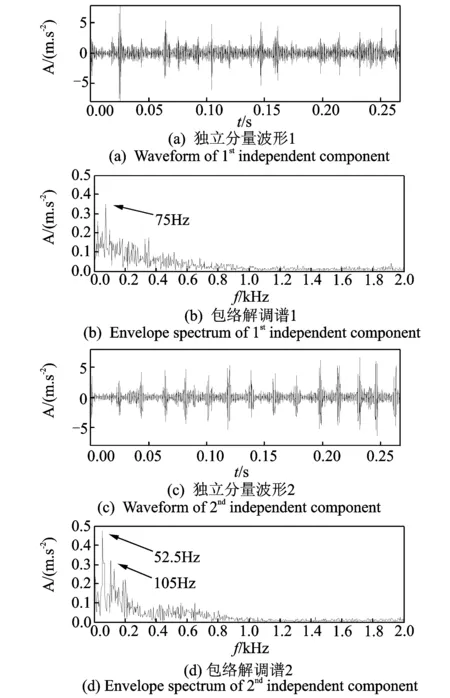
圖11 外圈滾動(dòng)體復(fù)合故障FastICA分離后的波形及包絡(luò)解調(diào)譜Fig.11 Waveform and envelope spectrums of outer and rolling element compound fault after FastICA

5 結(jié) 論

1) 利用雙樹(shù)復(fù)小波包變換具有近似平移不變性、較小的頻率混疊和有效降噪的優(yōu)點(diǎn)，對(duì)復(fù)合故障信號(hào)進(jìn)行分解，得到不同頻段的分量，對(duì)比傳統(tǒng)離散小波變換，雙樹(shù)復(fù)小波包分解效果更為理想。

2) 利用ICA對(duì)雙樹(shù)復(fù)小波包分解后的分量可以去除頻率混疊。

3) 將雙樹(shù)復(fù)小波包變換與ICA結(jié)合的方法應(yīng)用于復(fù)合故障診斷中，可以有效地的分離故障特征信息。

[1] Kingsbury N G. The dual-tree complex wavelet transform: a new technique for shift invariance and directional filters[J]. IEEE Digital Signal Processing Workshop,1998,98(1):2-5．

[2] Selesnick I W, Baraniuk R G, Kingsbury N G. The dual-tree complex wavelet transform[J]. IEEE Digital Signal Processing Magazine, 2005, 22(6): 123-151.

[3] Bayram I, Ivan W S. On the dual-tree complex wavelet packet and M-band transforms[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2298-2310.

[4] 翟振興. 基于小波變換的信號(hào)去噪研究[D]. 重慶：重慶大學(xué)，2010.

[5] 王娜,鄭德忠,劉永紅.雙樹(shù)復(fù)小波包變換語(yǔ)音增強(qiáng)新算法[J].傳感技術(shù)學(xué)報(bào)，2009,22(7):983-987.

Wang Na, Zheng Dezhong, Liu Yonghong. New method for speech enhancement based on dual tree complex wavelet packet transform[J]. Journal of Sensors and Actuators, 2009,22(7):983-987.(in Chinese)

[6] 吳定海,張培林,任國(guó)全，等.基于雙樹(shù)復(fù)小波包的發(fā)動(dòng)機(jī)振動(dòng)信號(hào)特征提取研究[J].振動(dòng)與沖擊,2010,29(4):160-164.

Wu Dinghai, Zhang Peilin, Ren Guoquan, et al. Feature extraction of an engine vibration signal based on dual tree wavelet package transformation[J]. Journal of Vibration and Shock, 2010, 29(4): 160-164. (in Chinese)

[7] 吳定海,張培林,張英堂，等.基于時(shí)頻奇異譜和RVM的柴油機(jī)故障診斷研究[J].機(jī)械強(qiáng)度,2011,33(3):317-323.

Wu Dinghai, Zhang Peilin, Zhang Yingtang, et al. Study on diesel engine faults diagnosis based on time frequency singular value spectrum and RVM[J]. Journal of Mechanical Strength, 2011,33(3):317-323. (in Chinese)

[8] 胥永剛,張發(fā)啟,何正嘉.獨(dú)立分量分析及其在故障診斷中的應(yīng)用[J].振動(dòng)與沖擊,2004,23(2):104-108.

Xu Yonggang, Zhang Faqi, He Zhengjia. Independent component analysis and its application to fault diagnosis [J].Journal of Vibration and Shock, 2004, 23(2):104-108. (in Chinese)

[9] 周曉峰, 楊世錫, 甘春標(biāo).一種旋轉(zhuǎn)機(jī)械振動(dòng)信號(hào)的盲源分離消噪方法[J].振動(dòng)、測(cè)試與診斷,2012,32(5):714-717.

Zhou Xiaofeng, Yang Shixi, Gan Chunbiao. De-noising vibration signal of rotating machinery with blind sources separation[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(5):714-717. (in Chinese)

[10]艾延廷,費(fèi)成巍,張鳳玲,等.ICA在航空發(fā)動(dòng)機(jī)振動(dòng)信號(hào)盲源分離中的應(yīng)用[J].振動(dòng)、測(cè)試與診斷,2010,30(6):671-674.

Ai Yanting, Fei Chengwei, Zhang Fengling, et al. Blind source separation for aero-engines vibration signal by independent component analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(6):671-674. (in Chinese)

[11]Hyvbrinen A, Oja E. Independent component analysis[J]. Neural Computing Surveys, 1999, 2: 94-128.

10.16450/j.cnki.issn.1004-6801.2015.03.018

*國(guó)家自然科學(xué)基金資助項(xiàng)目(51075009)；北京市優(yōu)秀人才培養(yǎng)資助計(jì)劃項(xiàng)目(2011D005015000006)

2013-02-24；

2013-04-09

TH133.3； TH165

胥永剛，男，1975年10月生，博士、副教授。主要研究方向?yàn)闄C(jī)械故障診斷、現(xiàn)代信號(hào)處理等。曾發(fā)表《雙樹(shù)復(fù)小波和奇異差分譜在滾動(dòng)軸承故障診斷中的應(yīng)用》(《振動(dòng)工程學(xué)報(bào)》2013年第26卷第6期)等論文。 E-mail: xyg@bjut.edu.cn