非均衡市場下房地產寡頭產量競爭研究
陳迅++賴純見
摘要:在非均衡市場下建立房地產寡頭產量競爭動態博弈模型,并分別用理論和數值模擬的方法對其演化加以分析。研究表明,在區域市場非均衡條件下,房地產寡頭可以通過重復博弈達成產量競爭均衡;在房地產開發生產技術、管理水平的特定階段和穩定的稅賦政策下,市場供需的非均衡狀態和地價房價比決定區域房地產寡頭產量博弈的均衡解、均衡穩定性和均衡演化路徑,從而決定房地產供給市場的類型。政府宜采取地價房價比控制、市場供需結構調節和稅收調整同步的方式調控房地產市場,政策效果相得益彰。
關鍵詞: 非均衡市場;房地產寡頭;博弈;納什均衡;混沌
中圖分類號:F224.32文獻標識碼:A文章編號:1003-7217(2015)03-0099-08
一、引言
區域房地產寡頭面臨共同的區域需求市場,其產量競爭更接近古諾博弈,是信息不對稱、有限理性下的動態行為博弈,且其所處市場環境可能是供需非均衡的。Jing Peng(2011)等研究了具有不變線性成本的延遲有限理性三寡頭博弈,發現合適的延遲參數能夠擴大系統的穩定區域[1] 。Lu(2011)等研究表明,決策狀態延遲能夠擴大均衡穩定域并延緩分岔[2]。易余胤(2004)等的研究發現溢出效應能增加博弈達到Nash均衡的可能性[3]。Fabio(2010)研究發現寡頭的類型影響均衡的穩定性和其失穩后的復雜動力學演化,但并不影響均衡解本身[4]。Leonard(2009)研究表明,在異質混合雙寡頭框架下,由于環境稅收與減排的影響,私有化將導致社會福利降低[5]。姚洪興(2005)等研究發現企業加快廣告投入量的調整速度,會導致博弈系統的不穩定[6]。Tnu(2006)的研究表明靜態古諾博弈均衡解的存在性與參與博弈的寡頭數量無關[7]。牟玲玲(2010)等分析了寡頭博弈模型演化的復雜性態[8]。童光毅(2008)等針對房地產市場的非均衡狀態, 以半參數(拓展)回歸模型解釋了我國房地產價格持續大幅上漲的原因[9]。闕彬(2011)等在聚合方程下實證分析了房地產市場非均衡狀態[10]。姚洪興(2008)等研究了均衡市場下房地產投資決策博弈模型的復雜性[11]。現有市場模型側重于宏觀方面,缺乏對其區域特性、地區差別和市場主體行為(微觀)等因素的考慮;沒有反映出均衡與非均衡市場共存的現狀及其內在聯系。本文擬從區域房產商的產量競爭決策行為及區域市場供求的微觀視角,研究區域房地產市場(非)均衡狀態、管控政策等與產量分配機制關系的經濟規律,期望能為行業運營實踐、管控政策制定提供理論參考。
二、模型建立
假設:(1)宏觀經濟政策、經濟形勢相對穩定,經濟系統運行勿受突變擾動;(2)房地產市場可能呈現非均衡;(3)寡頭均以贏利為目的,公益性房產供給不進入市場;(4)寡頭是有限理性的,即普遍存在的“短視預期”和“羊群效應”[12]傳導所致。我們定義“短視預期”為一期即項目運營平均周期上的有限理性預期,能夠根據現有的信息如當期邊際利潤、價格預期下一期的價格水平,或者至少二者差異的方差很小,可以通過線性的決策系數加以矯正,從而決定下期產量,謂之“一階理性”;(5)寡頭間不存在合謀,產品同質或具有等價替代性,即符合古諾模型的市場結構特點[11,13] 。
從土地使用權買賣行為至房地產產品售罄(或留下一定量的尾盤,不同房地產生產者各異),有一個較長的產銷期(如2~5年),但出讓土地時,地方政府和房產商均不能確切知道土地未來物化至商品房中的真實價值,一般是根據當期(如t期)對未來建成商品房的預期價格pe(t+1)來決策。根據假設(4),pe(t+1)等于或近似于t+1期實際交易價格p(t+1)①。從土地交易雙方關于房地產行業的知識和信息面來看,這也是切合實際的。t期交易的土地價格是t+1期房地產的重要成本,會影響到t+1期房產實際交易價格,進而影響房地產供應量。
若某區域t期房地產市場需求曲線為p(t)=a-bD(t)②,其中a>0,b>0為常系數,a表示區域房地產的最高價格;D(t)>0為t期市場需求。該區域市場上n個寡頭生產可代替房地產產品,進行產量競爭。第i個房地產寡頭t-1期決策生產t期面市供給量為qi(t),i=1,2,…,n,則t期房地產市場供給S(t)=∑ni=1qi(t)。若區域市場非均衡,第i個寡頭t期面臨的需求量為qi(t)(1+σi),其中σi≥-1,i=1,2,…,n。σi>0表示超額需求率;-1≤σi<0表示超額供給率,則1+σi反映房地產銷售去化率;σi=0時表示供需均衡。因此,該區域t期市場需求D(t)=∑ni=1qi(t)(1+σi),那么,市場需求曲線為:
p(t)=a-b∑ni=1qi(t)(1+σi) (1)
財經理論與實踐(雙月刊)2015年第3期2015年第3期(總第195期)陳迅.賴純見:非均衡市場下房地產寡頭產量競爭研究
區域t期(t-1期決策的)樓面地價為cpe(t)=cp(t),其中0 πi(t)=(I′i-γ)(a-b∑ni=1qi(t)(1+σi))qi(t)
i=1,2,…,n (2)
令Ii=I′i-γ=1-γ-c1-ri,則Ii為第i個寡頭的銷售凈利率。第i個寡頭第t期邊際利潤函數為:
π′i(t)=πi(t)qi(t)=Ii(a-b∑nj=1qj(t)(1+
σj)-bqi(t)(1+σi))i=1,2,…,n(3)
在非對稱需求信息、一階理性下,多寡頭進行動態古諾博弈。寡頭們依據其當期產量及邊際利潤情況來決策下一期產量的調整。第i個寡頭t期邊際利潤π'i(t)>0,則t+1期產量qi(t+1)在qi(t)基礎上調整增加,反之則調整降低[14]。
此外,寡頭還會根據t期供求狀況,對t+1期產量作修正:當t期存在超額供給即-1≤σi<0,則t+1期產量調整σiqi(t);當第t期存在超額需求即σi>0,則超額需求自動積蓄形成下期需求,對t+1期產量不作額外修正。從而,第i個寡頭參與古諾重復博弈的產量動態調整機制:
qi(t+1)=qi(t)+αi(qi(t))π'i(t)+Δqi(t)
i=1,2,…,n (4)
其中αi(qi(t))>0,表示第i個寡頭產量動態調整速率;Δqi(t)=σiqi(t)σi<00σi≥0,是對t期超額供給的產量修正。假設動態調整速率αi(qi(t))=αiqi(t),i=1,2,…,n。由式(3)和式(4)可以得到多個寡頭產量決策重復博弈模型:
qi(t+1)=qi(t)+αiqi(t)Ii(a-
b∑nj=1qj(t)(1+σj)-bqi(t)(1+σi))+Δqi(t)
Δqi(t)=σiqi(t)σi<00σi≥0
Ii=1-γ-c1-rii=1,2,…,n
D(t)=∑ni=1qi(t)(1+σi)
S(t)=∑ni=1qi(t)(5)
三、模型分析
為了簡化計算過程,重點討論雙寡頭的情形:
q1(t+1)=q1(t)+α1q1(t)I1(a-2bq1(t)
(1+σ1)-bq2(t)(1+σ2))+Δq1(t)
q2(t+1)=q2(t)+α2q2(t)I2(a-2bq2(t)(1+
σ2)-bq1(t)(1+σ1))+Δq2(t)
Δqi(t)=σiqi(t)σi<00σi≥0,i=1,2
Ii=1-γ-c1-ri,i=1,2
D(t)=q1(t)(1+σ1)+q2(t)(1+σ2)
S(t)=q1(t)+q2(t)(6)
對于系統(6)令qi(t+1)=qi(t),i=1,2。(1)若σi≥0,i=1,2,可求得其四個均衡點:E1=0,0,E2=a2b(1+σ1),0,E3=0,a2b(1+σ2),E4=a3b(1+σ1),a3b(1+σ2);(2)若σi<0,i=1,2,系統均衡點:E1=0,0,E2=a+σ1α1I12b(1+σ1),0,E3=0,a+σ2α2I22b(1+σ2),E4=a+2σ1α1I1-σ2α2I23b(1+σ1),a+2σ2α2I2-σ1α1I13b(1+σ2);(3)若σi≥0而σj<0,i≠j,i,j=1,2,如σ1≥0,σ2<0,則系統均衡點:E1=0,0,E2=a2b(1+σ1),0,E3=0,a+σ2α2I22b(1+σ2),E4=a-σ2α2I23b(1+σ1),a+2σ2α2I23b(1+σ2),由對稱性,當σ2≥0,σ1<0時,系統(6)有近似均衡點(略);其中Ii=1-γ-c1-ri,i=1,2。下面按以上三種均衡情形,分析博弈系統的特性。博弈系統(6)的Jacobi矩陣為:
J=1+α1I1(a-4bq1(t)(1+σ1)-bq2(t)(1+σ2))+sgn (σ1)σ1-α1I1bq1(t)(1+σ2)-α2I2bq2(t)(1+σ1)1+α2I2(a-4bq2(t)(1+σ2)-bq1(t)(1+σ1))+sgn (σ2)σ2
其中:
Ii=1-γ-c1-ri
sgn (σi)=0σi≥0
1σi<0i=1,2 (7)
命題1當σi≥0,i=1,2時,即在均衡情形(1)下③,區域房地產寡頭產量競爭博弈均衡和供給市場類型取決于地方政府土地價格參數c,而與市場供需非均衡程度σi無關;存在Nash均衡解且其穩定性條件與均衡市場下相似[15]。
命題2 當σi<0,i=1,2時,即在均衡情形(2)下④,區域房地產寡頭產量競爭博弈均衡和供給市場類型取決于市場的非均衡程度σi和地方政府土地價格參數c的匹配性;產量決策博弈出現零產量、壟斷和寡頭壟斷幾種形式的局部穩定均衡;不存在Nash均衡解。
命題3 當σ1≥0,σ2<0時,即在均衡情形(3)下⑤,區域房地產寡頭產量競爭博弈均衡和供給市場類型取決于寡頭2的市場非均衡程度σ2和地方政府土地價格參數c的匹配性;產量決策博弈出現零產量、壟斷(由寡頭1)和寡頭壟斷幾種形式的局部穩定均衡;不存在Nash均衡解。
四、數值模擬分析
(一)命題1情形博弈系統分析
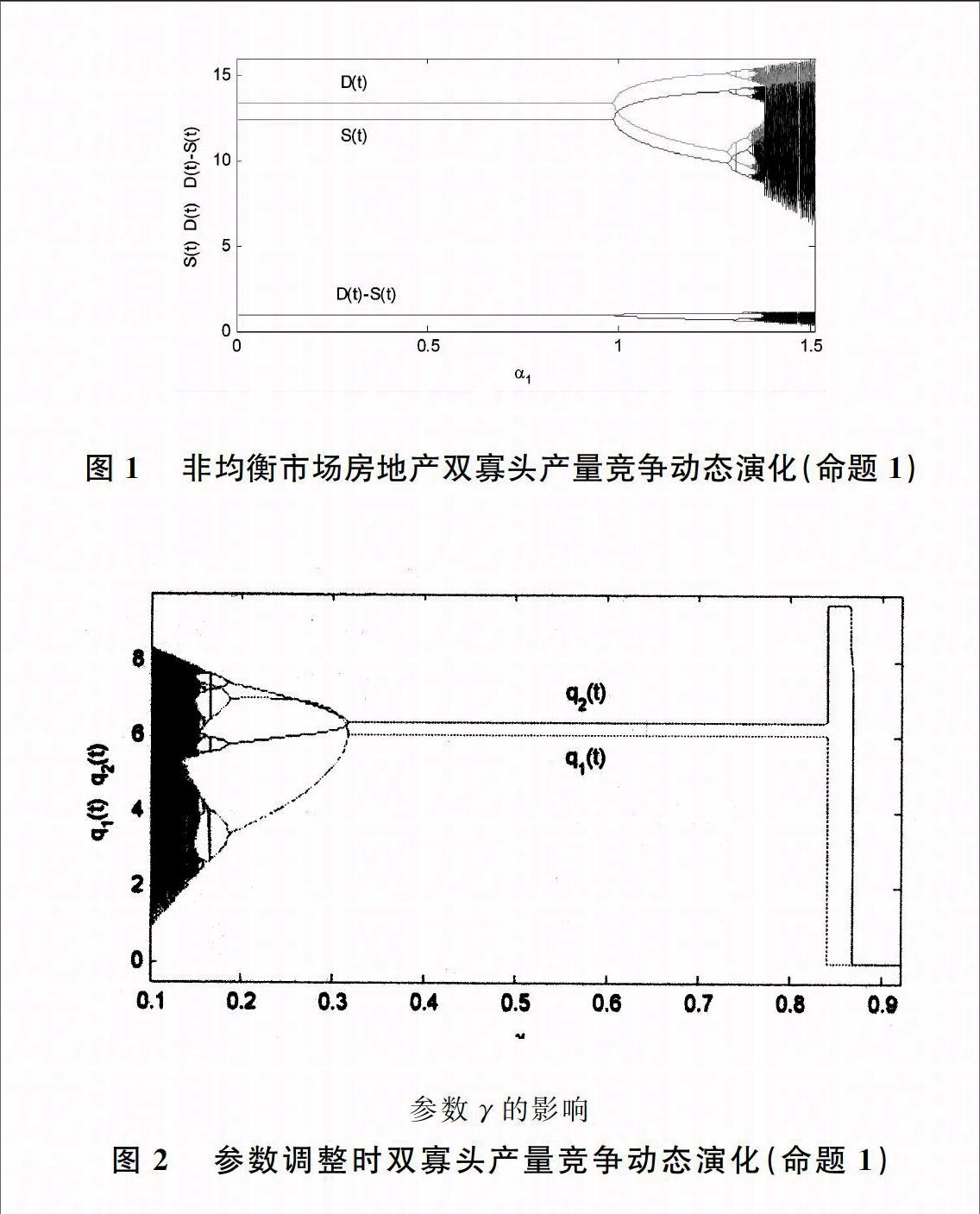
1.博弈系統演化。取參數值a=10,b=0.5,c=0.3,α2=0.2,r1=0.5,r2=0.4,σ1=0.1,σ2=0.05,初值q10=3.5,q20=8.6,雙寡頭博弈系統動態演化過程參見賴純見、陳迅的研究[15]。圖1表明市場均衡并不是房地產寡頭博弈Nash均衡的前
圖1非均衡市場房地產雙寡頭產量競爭動態演化(命題1)
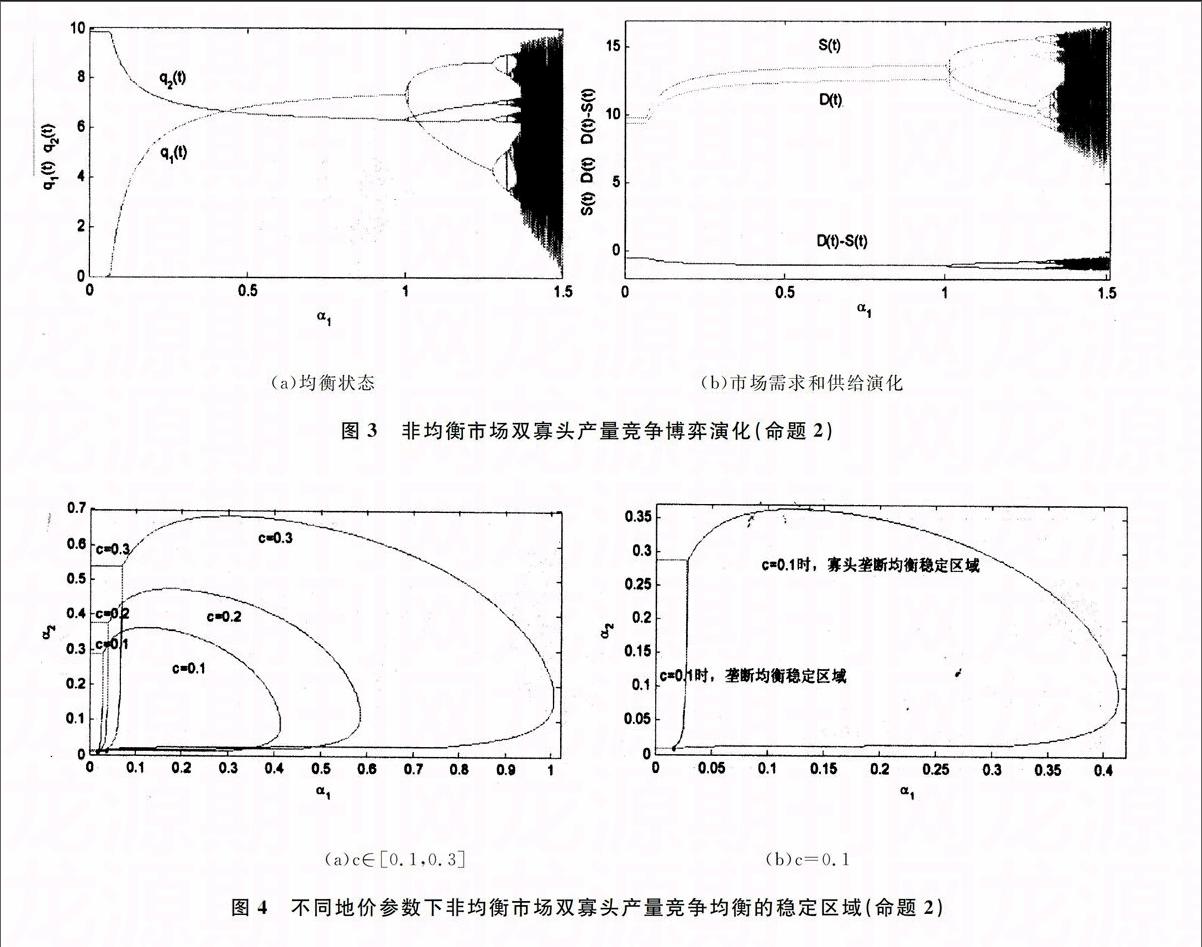
參數γ的影響
圖2參數調整時雙寡頭產量競爭動態演化(命題1)
提條件,在市場超額需求下可以形成穩定Nash均衡產量分配。
2.博弈均衡的穩定域。根據命題1,均衡的穩定性僅取決于政府地價參數c(證明詳見附錄A),取參數值c∈[0.1,0.4],繪出產量博弈寡頭壟斷和壟斷情形Nash均衡解的穩定區域[15]。
3.地價房價比、稅收和供求非均衡對博弈的影響。取參數值 a=10,b=0.5,α1=0.5,α2=0.2,r1=0.5,r2=0.4,σ1=0.1,σ2=0.05恒定,地價參數c調整時,雙寡頭博弈動態演化呈現倒分岔形態過程[16]。圖2表明稅收γ和地價參數c對博弈系統的影響是相似的,所以,政府采用這兩方面的調控政策的效果具有替代性。(二)命題2情形博弈系統分析
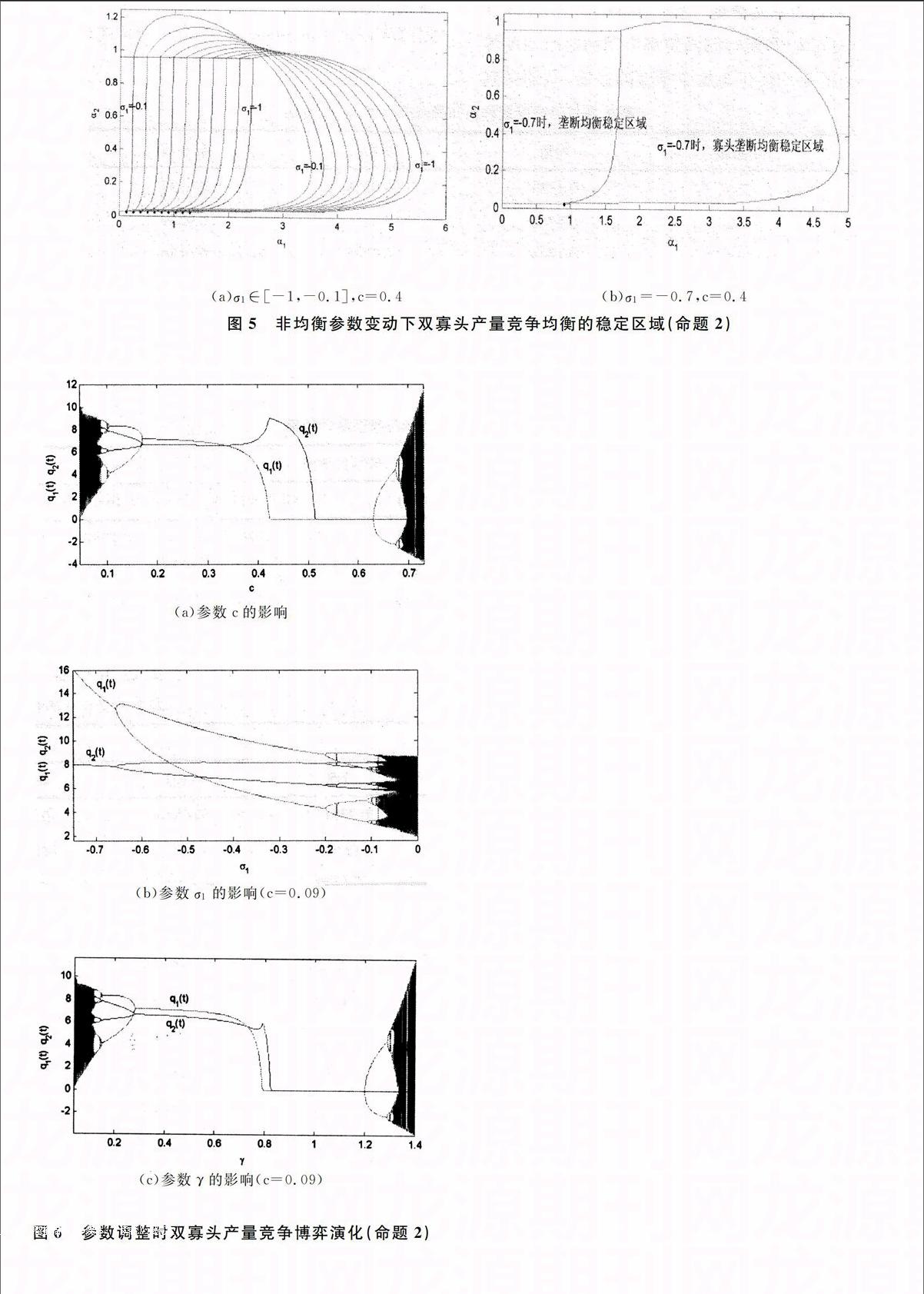
1.博弈系統演化。取參數值a=10,b=0.5,c=0.3,α2=0.2,r1=0.5,r2=0.4,σ1=-0.1,σ2=-0.05,初值為q10=3.5,q20=8.6,得到均衡解隨α1的變動形態,見圖3(a)。這與理論分析的情形(2)均衡解E3寡頭2壟斷(0<α1≤0.067)、E4寡頭壟斷均衡(0.067<α1≤1.003)相符,然后通過倍周期分岔進入混沌區域(α1>1.003)。圖3(b)反映寡頭產量博弈均衡是在市場非均衡下達成的。由圖3看到,在同一地價參數c=0.3下,系統可以呈現壟斷均衡或寡頭壟斷均衡,這與命題1的情況是完全不同的。政府已經不能單靠地價房價比的控制來實現市場類型管控和調節。
2.博弈均衡的穩定域。根據均衡穩定性條件④,固定參數a=10,b=0.5, r1=0.5,r2=0.4,σ1=-0.1,σ2=-0.05,初值為q10=3.5,q20=8.6,變動c、α1、α2可用數值分析更直觀地描述,見圖4。
(a)均衡狀態 (b)市場需求和供給演化
圖3非均衡市場雙寡頭產量競爭博弈演化(命題2)
(a)c∈[0.1,0.3] (b)c=0.1
圖4不同地價參數下非均衡市場雙寡頭產量競爭均衡的穩定區域(命題2)
圖4(a)是不同的地價參數c下的均衡穩定域,隨地價參數c遞增而擴大;但當c≥0.4時,穩定的均衡類型是壟斷還是寡頭壟斷還要取決于市場非均衡參數σ1,σ2。取c=0.4,間隔0.1變動市場參數σ1繪制博弈均衡穩定域,見圖5(a)、(b)。
3.地價房價比、稅收和供求非均衡對博弈的影響。取參數α1=0.5、α2=0.2不變,只調節參數c、σi、γ的情形,見圖6。圖6表明參數c、σi、γ均能在不同程度上改變系統的混沌態,而圖6(a)和(c)演化過程近似,表明土地價格和稅負管理政策效果具有替代性。
(a)σ1∈[-1,-0.1],c=0.4 (b)σ1=-0.7,c=0.4
圖5非均衡參數變動下雙寡頭產量競爭均衡的穩定區域(命題2)
(a)參數c的影響
(b)參數σ1的影響(c=0.09)
(c)參數γ的影響(c=0.09)
圖6參數調整時雙寡頭產量競爭博弈演化(命題2)
(三)命題3情形博弈系統分析
1.博弈系統演化。取a=10,b=0.5,c=0.3,α2=0.2,r1=0.5,r2=0.4,σ1=0.1,σ2=-0.05,初值為q10=3.5,q20=8.6,得到寡頭壟斷穩定均衡解隨α1調整的演化形態,見圖7(a);其他參數不變,若取α1=0.5,可得該系統均衡隨α2調整的演化形態,大致經歷以下過程:壟斷(由寡頭1)E2(0<α2≤0.026)、寡頭壟斷E4(0.026<α2≤0.669),然后通過倍周期分岔進入混沌區域(α2>0.669),見圖7(b)。寡頭2在全局最優選擇下作依賴于市場狀況的存量調整,從而該均衡結果是次優的,不存在Nash均衡。圖7(c)、(d)表明,在總需求大于總供給下,房地產寡頭博弈也可以達成穩定均衡。
2.博弈均衡的穩定域。根據穩定性條件⑤,固定參數a=10,b=0.5, r1=0.5,r2=0.4,σ1=0.1,σ2=-0.05,初值為q10=3.5,q20=8.6,變動c、α1、α2繪制出壟斷(由寡頭1)均衡E2和寡頭壟斷均衡點E4的穩定性域,見圖8(a)、(b)。
調整市場非均衡參數σ1、σ2繪制出系統的均衡穩定域,見圖9。圖9(a)表明,超額需求σ1變動不會改變系統均衡穩定區域;而圖9(b)則反映出超額供給參數σ2的變動會改變系統的均衡穩定性,而且這種影響并不獨立于地價參數c,如圖9(b)和圖8(a)形態近似,但穩定域空間隨市場波動較大。所以,同步采取限制地價房價比和調整稅負水平政策的同時,還應加強市場供需結構的管理,避免各項調控政策的施行效果將呈蹺蹺板現象。
3.地價房價比、稅收和供求非均衡對博弈的影響。取σ1=0.1、σ2=-0.05、α1=0.5、α2=0.2,其他參數不變,調整地價參數c,發現系統呈現與命題2下類似的演化過程,見圖10(a)。市場非均衡因素σ2的變動并不能使系統在均衡狀態和混沌狀態間轉換,見圖10(b)。
圖10(c)與圖10(a)演化形態類似,說明房地產業承擔的綜合稅負與地價參數c對房地產系統的影響是近似的。
(a)迭代均衡( 0<α1<1.44) (b)迭代均衡(0<α2<1.06)
(c)市場需求和供給演化(0<α1<1.44) (d)市場需求和供給演化(0<α2<1.06)
圖7非均衡市場雙寡頭產量競爭博弈演化(命題3)
(a) E2、E4,c∈[0.1,0.4] (b)E2、E4,c=0.1
圖8地價參數變動下非均衡市場雙寡頭產量競爭均衡的穩定區域(命題3)
(a)E2、E4,c=0.3,σ1∈(0,1) (b) c=0.3,σ2∈[-1,-0.1]
圖9非均衡參數變動下雙寡頭產量競爭均衡的穩定區域(命題3)
(a)參數c的影響
(b) 參數σ2的影響(c=0.08)
(c)參數γ的影響(c=0.3)
圖10參數調整時雙寡頭產量競爭博弈演化(命題3)
五、結語
本文建立的模型是對經典的靜態完美Cournot模型進行特定的動力學改良,更符合房地產行業產量分配動態演化的實際情況。以二寡頭產量競爭為例,研究區域房地產非均衡市場下動態博弈混沌態、壟斷均衡、寡頭壟斷均衡、滯漲均衡的均衡解及其漸進穩定區域特性。研究結果論與建議:(1)房地產寡頭產量競爭博弈可達成均衡,但市場的非均衡性會影響產量競爭博弈Nash均衡的存在性及穩定性;該博弈在市場均衡下的情形僅是其在非均衡市場下的一個特例;(2)區域房地產供給市場類型主要取決于市場供需非均衡程度、行業稅負率和地方政府對土地價格管理,政府的行業管控措施適宜從這三方面著手;(3)地價房價比控制、稅負水平管理兩方面調控政策具有替代性,但均受制于市場供需結構關系。同步采用供需結構管理、地價房價比控制和稅負管理的組合調控政策,效果更佳,且能夠有效杜絕調控政策實施中的蹺蹺板效應;(4)房地產市場宏觀管控政策不宜通過直接作用于供給量或需求量以實現全民普惠,謹防市場在全面超額需求和全面超額供給間來回轉換,如限購等直接行政干預手段可能將市場引向更加難以掌控的反向局面。
注釋:
①理論上的綜合平均價格,忽略房地產類別、方位和銷售時間先后等因素形成的復雜的、持續變化的銷售價格差異。
② 將需求函數改變成形式為p(t)=a-bD(t)-b1D(t)2…-bn-1D(t)n的多項式,模型相關研究結論與本文一致,為簡化計算,本文僅研究線性需求函數的情形。
③篇幅所限,證明過程參見文獻[16],其結論完全一致,即當寡頭普遍存在超額需求時,區域房地產產量競爭均衡穩定性和供給市場類型取決于地方政府地價管控參數c,而與市場供需非均衡程度σi無關,原因在于商品房供給時滯效應和運營成本中土地成本的占比差異。這也表明市場均衡條件下的該產量競爭博弈均衡僅是非均衡市場下情形的一個特例。
④證明:(1)E1處的Jacobi矩陣為JE1=1+aα1I1+σ1001+aα2I2+σ2。它的兩個特征值λi=1+aαiIi+σi,其中a>0,αi>0,-1≤σi<0, i=1,2。E1的穩定條件λi<1,解不等式可以得出-2-aαiIi<σi<0且-2aαi
(3)由對稱性,可以相應得出E3的穩定條件。
(4)E4的Jacobi矩陣為JE4=1-23aα1I1-43σ1+2α1I13α2I2σ2-1+σ23(1+σ1)(aα1I1+2σ1-α1I1α2I2σ2)-1+σ13(1+σ2)(aα2I2+2σ2-α2I2α1I1σ1)1-23aα2I2-43σ2+2α2I23α1I1σ1,其特征多項式D(λ)=D0+D1λ+D2λ2, 其中D2=1,D1=-2+23aα1I1+23aα2I2+43σ1-2α2I23α1I1σ1-2α1I13α2I2σ2+43σ2,D0=1-23αα1I1-23αα2I2+13α2α1I1α2I2-43σ1+13αα2I2σ1+2α2I23α1I1σ1-2α2I23α1I1σ21-43σ2+13αα1I1σ2+2α1I13α2I2σ2+53σ1σ2-2α2I12α1I2σ22。根據Jury離散系統穩定性的充要條件,均衡點E4穩定性條件為D(1)=D0+D1+D2>0
D(-1)=D0-D1+D2>0
|D0| ⑤證明:(1)E1的穩定條件-2aα1
D(-1)=D0-D1+D2>0
|D0| 參考文獻: [1]Jing Peng,Zehua Miao,Fang Peng.Study on a 3-dimensional game model with delayed bounded rationality[J].Applied Mathematics and Computation, 2011,218(5):1568-1576. [2]Lu Yali.Dynamics of a delayed duopoly game with increasing marginal costs and bounded rationality strategy[J].Procedia Engineering,2011,15(4):4392-4396. [3]易余胤,盛昭瀚,肖條軍.具有溢出效應的有限理性雙寡頭博弈的動態演化[J].系統工程學報,2004,19(3):244-250. [4]Fabio Tramontana. Heterogeneous duopoly with isoelastic demand function[J].Economic Modelling, 2010,27(1):350-357. [5]Leonard F.S.Wang,Jean Wang.Environmental taxes in a differentiated mixed duopoly[J].Economic Systems,2009,33(4):389-396. [6]姚洪興,徐峰.雙寡頭有限理性廣告博弈模型的復雜性分析[J].系統工程理論與實踐,2005,25(12):32-37. [7]Tnu Puu. On the stability of cournot equilibrium when the number of competitors increases[J]. Economic Behavior & Organization,2006,16(3-4):1606-1618. [8]牟玲玲,陳立文,張俊玲. 非均衡房地產市場博弈行為復雜性研究[J].系統工程學報,2010,25(6):824-828. [9]童光毅,劉星.我國房地產價格的非均衡性[J].管理世界,2008,(1):175-177. [10]闕彬.房地產市場供求非均衡[M].成都:西南交通大學出版社,2011. [11]姚洪興,王國棟.一類房地產投資模型的復雜性分析[J].統計與決策,2008,253(1):56-57. [12]陳林,朱衛平.基于二手市場與理性預期的房地產市場機制研究[J].管理科學學報,2011,14(2):61-70. [13]侯文宇.古諾線性模型與中國房地產[J].首都師范大學學報(自然科學版),2008,29(5):1-6 [14]馬軍海,彭靖. 延遲決策對一類寡頭博弈模型的影響分析[J].系統工程學報,2010,25(6):812-817. [15]賴純見,陳迅.房地產寡頭有限理性博弈模型的復雜性分析[J].系統工程學報,2013,28(3):285-296. (責任編輯:漆玲瓊)

