基于蟻群算法的LFM信號參數估計

關曉謙，劉東平，李東濤

(中國洛陽電子裝備試驗中心，河南濟源454650)

1 引 言

線性調頻(Linear Frequency Modulation，LFM)信號是在脈沖持續期間內信號頻率連續線性變化的信號，是一類非常重要的非平穩信號，被廣泛應用于雷達、聲納和通信等信息系統［1－2］。調頻斜率和起始頻率作為線性調頻信號的2個重要參數，其估計問題一直是LFM信號處理領域的研究熱點和難點。目前，已經出現了很多比較成熟的算法，比如Radon－Wigner變換、分數階傅里葉變換(fractional Fourier transform，FRFT)和最大似然估計(ML)等方法［3－7］。其中基于 FRFT 的LFM信號參數估計方法最受關注。但是，該方法每檢測一個信號都要對信號分別求所有旋轉角α∈［0，π］的 FRFT，再進行二維搜索、濾波以及FRFT逆變換，計算量大。而且對信號反復進行FRFT、濾波和FRFT逆變換也會給弱信號帶來誤差。

文獻［8］提出利用LFM信號能量一定時，在相同的時寬范圍內，其頻譜幅度平方與調頻斜率呈反比的特性，通過在固定區間上改變解線調參考信號的調頻斜率，逐步進行搜索估計信號參數的算法。該算法在一定程度上解決了分數階Fourier變換法的大運算量問題，但決定該算法估計精度的搜索步長這一參數，卻受算法運算量的制約，步長太大估計誤差變大，步長太小則運算量急劇上升，算法無法平衡估計精度和運算量之間的矛盾。針對此問題，本文提出了基于蟻群算法優化的參數估計算法。

2 LFM信號參數估計原理

當時寬帶寬積遠遠大于1時，LFM信號的幅譜近似為無菲涅爾起伏的矩形譜，其頻譜寬度近似等于信號帶寬B［9］。設LFM信號為:

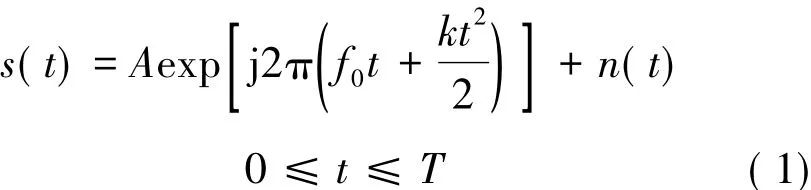
式中:A為信號幅度;f0為載頻;k為調頻斜率;n(t)零均值的高斯白噪聲;T為信號的時寬。

根據帕斯瓦爾定理可知，s(t)的功率P可表示為:

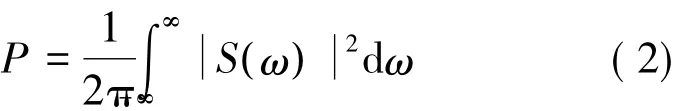
式中:S(ω)是信號s(t)的頻譜。

當BT＞＞1時，式(2)可近似化簡為:

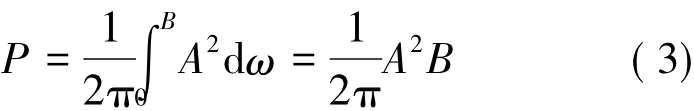
將調頻斜率k與帶寬B和時寬T之間的關系B=kT代入式(3)可得:

對于一定時寬的LFM信號，其信號能量總是可測的，即信號能量是一定的，由式(4)可知，在相同時寬范圍內，其頻譜幅度平方與調頻斜率成反比。調頻斜率越小，對應的頻譜幅值就越大，其頻譜最大幅值對應譜線處的頻率即為起始頻率的真值。

根據LFM信號的以上性質，對LFM信號的調頻斜率和起始頻率的估計的步驟如下:

(1)將調頻斜率的變化范圍［kmin，kmax］以Δk為步長劃分為一系列離散值，記為ki(i=1，2，…，N)，N為離散值的總數。

(2) 分別用 exp［－jπkit2］(i=1，2，…，N)和 s(t)相乘，得到N組解調后的信號:

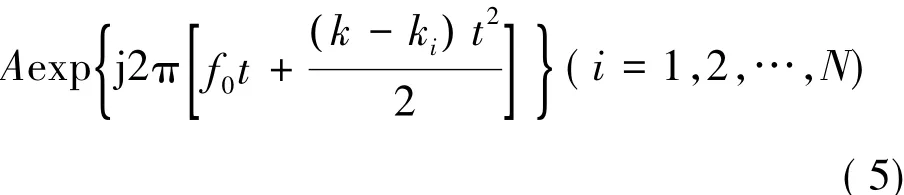
(3)分別對式(5)做傅里葉變換，得到N組頻譜對應的 N 個最大幅值，記為 A1，A2，…，AN，與此N個最大幅值對應的頻率值記為f1，f2，…，fN。

(4)對 A1，A2，…，AN進行比較，找出其中的最大值Amax，設Amax=Al，則得到調頻斜率的估計值ke=kl，起始頻率的估計值為fe=fl。

3 基于蟻群算法的參數估計算法

蟻群算法［10］(Ant Colony Optimization，ACO)是近年來才提出的一種基于種群尋優的啟發式搜索算法，由意大利學者M．Dorigo等于1991年首先提出。該算法受到自然界中真實蟻群集體行為的啟發，利用真實蟻群通過個體間的信息傳遞、搜索從蟻穴到食物間的最短路徑的集體尋優特征，來解決一些離散系統中優化的困難問題。本文將蟻群算法的全局優化和啟發式尋優的特點應用于LFM信號參數估計，將LFM信號參數估計問題轉化為函數求極值問題，利用蟻群算法對函數尋優，提出了基于蟻群算法的LFM信號參數估計算法，算法步驟如下:

Step 1 初始化變量:設定調頻斜率k的變化范圍［kmin，kmax］，并以 Δk為步長對其離散化，如下式:

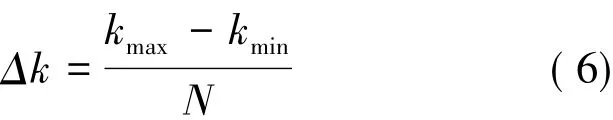
令調頻斜率離散化后各結點初始信息素為τ1×N=U，螞蟻數目 M。

Step 2 計算各結點的選擇概率:

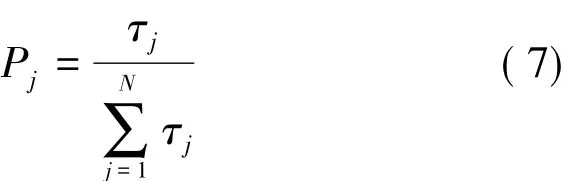
節點選擇采用輪盤賭的算法進行選擇，確保信息素濃度高的節點被選擇的概率高，輪盤賭算法在實際應用中如式A(n)=表示前 n個不同節點的選擇概率和。釋放蟻群中所有的M只螞蟻，同時在區間［0，1］上隨機生成M個小數，與M只螞蟻一一對應，判斷每個隨機數位于區間［A(n－1)，A(n)］時所對應的n值，則認為M個n值所對應的kn就是被這群螞蟻選擇的調頻斜率，這樣既保證了信息素濃度高的節點被選擇的概率高，又避免了每只螞蟻均按照同一概率選擇kn。

Step 3 構造目標函數:

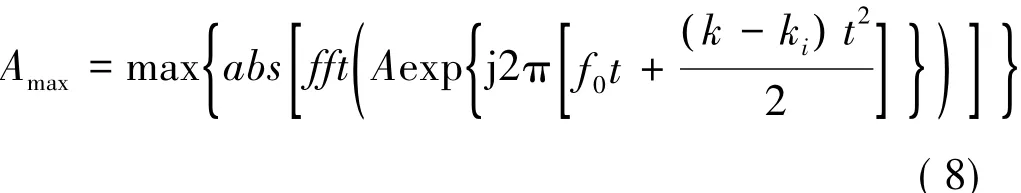
式中:abs(· )表示對信號去模運算;fft(· )表示對信號進行傅里葉變換。

Step 4 設置算法終止條件:若最近五次迭代搜索到的最優值之間相差小于某一設定值，則認為算法已搜索到最優值，算法終止;否則，完成所設定迭代次數，算法終止。

將式(7)選擇的kn代入式(8)，計算目標函數值，若滿足算法終止條件，則算法終止，設Amax取最大值時kn=k0，則k0即為信號調頻斜率的最優估計值。若不滿足算法終止條件，則更新信息素，并返回Step2，滿足算法終止條件。

Step 5 把kn=k0代入式(5)中，求其傅里葉變換，找出對應于頻譜最大的頻率f，即為起始頻率的最優估計值。

4 仿真結果分析

4.1 參數估計結果分析

為了驗證算法的可靠性，取一個單分量LFM信號進行仿真驗證。設接收到的LFM信號模型如式(1)所示，為了便于計算取幅度值A=1，信號起始頻率為350 Hz，調頻斜率k=60 Hz/s，其估計范圍為［40 Hz/s，80Hz/s］，信號觀測長度 T=5 s，采樣頻率為fs=2 kHz，信號信噪比為－20 dB;螞蟻個數為100，初始信息素U=15，信息素的揮發度為0．1。分別用本文算法、文獻［8］算法和FRFT算法對此信號模型參數進行估計，經過14次迭代(更新了14次信息素)得到參數估計結果，估計結果見表1。

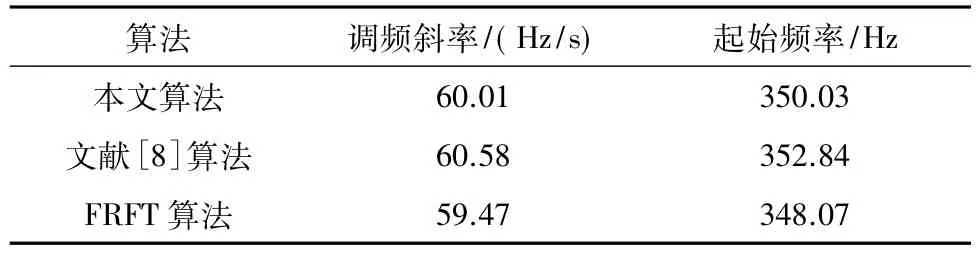
表1 信號參數估計結果Tab．1 Result of signal parameter estimate

分析參數估計結果可知:首先，由于算法參數都是在低信噪比條件先得到的，因此這三種算法都能較好地估計出信號的參數，且本文算法的參數估計精度高于文獻［8］算法和FRFT算法;其次，起始頻率的估計精度低于調頻斜率的估計精度，且文獻［8］算法和FRFT算法更差，其主要原因是:首先對信號調頻斜率進行估計，然后利用估計結果進而估計出起始頻率，導致了誤差的積累和放大，尤其是文獻［8］算法和FRFT算法要經過多次變換和逆變換，所以對信號的起始頻率估計精度就更差。

在信號參數不變的情況下，改變噪聲的強度，分別采用本文算法、文獻［8］算法和FRFT算法進行參數估計。重復進行30次Monte－Carle仿真，計算參數估計的均方誤差(Mean Square Error，MSE)，圖1和圖2分別給出了調頻斜率和起始頻率的參數估計均方誤差隨信噪比(SNR)的變化曲線。

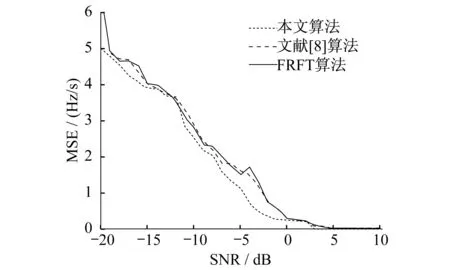
圖1 調頻斜率MSE隨信噪比變化曲線Fig．1 Changing curve of chirp rate MSE followed with the SNR

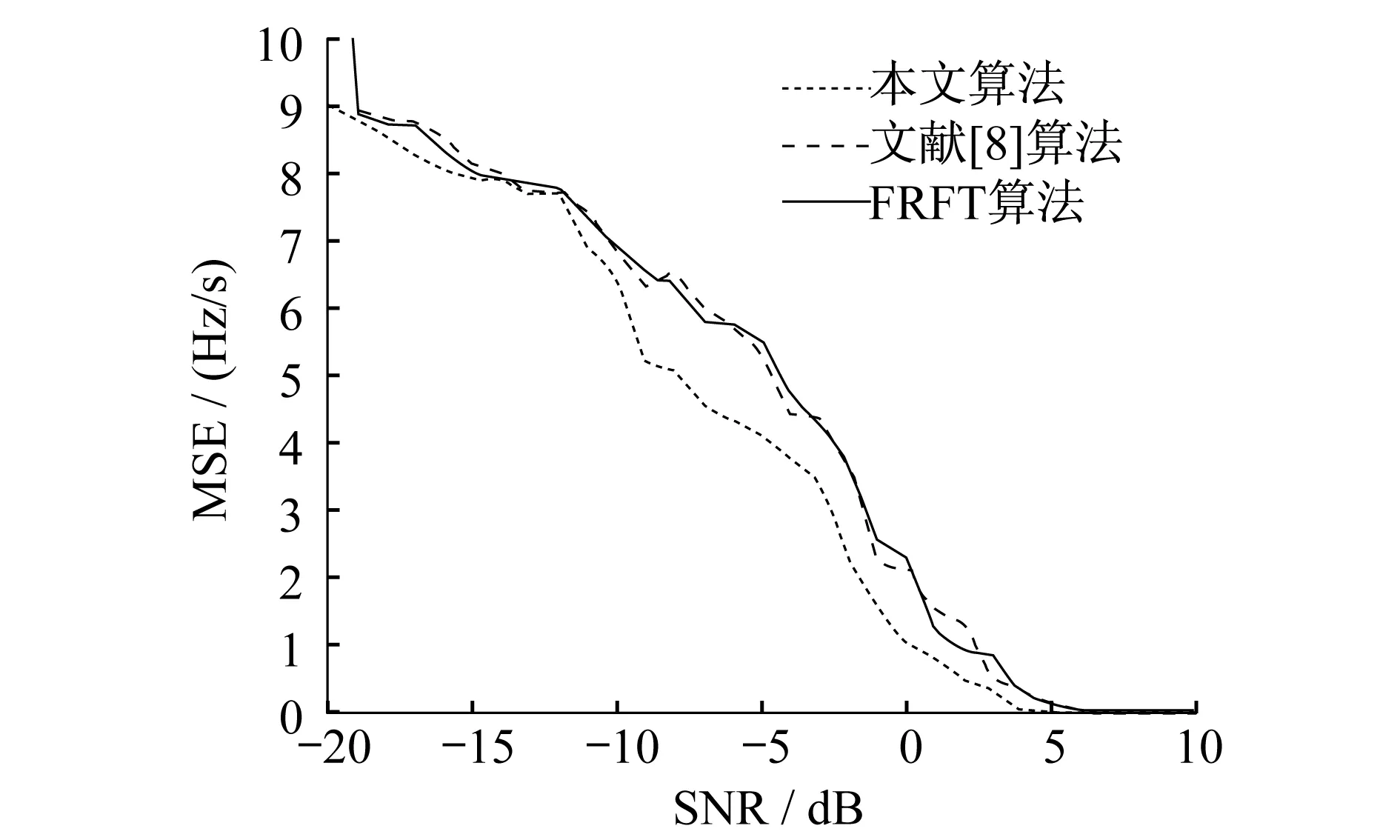
圖2 起始頻率MSE隨信噪比變化曲線Fig．2 Changing curve of origination frequency MSE followed with the SNR

圖1 和圖2進一步表明:調頻斜率的估計精度高于起始頻率的估計精度，此外，隨著信噪比的增加，信號參數估計誤差呈不斷下降的趨勢。

4.2 算法計算量分析

本文蟻群算法中螞蟻個數選為100，迭代次數選為50，則蟻群算法對調頻斜率的估計過程如圖3所示。

由圖3可知，當算法迭代到第14次的時候達到了算法終止條件要求的估計精度。FFT計算的復雜度為o( M ×log M)［11］，其中 M 為采樣點數，則本文算法復雜度為:

o(14×100×M×log M)=o(1 400×M×log M)

文獻［6］算法的復雜度為:

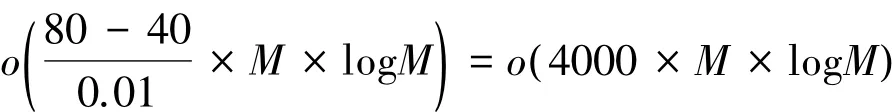
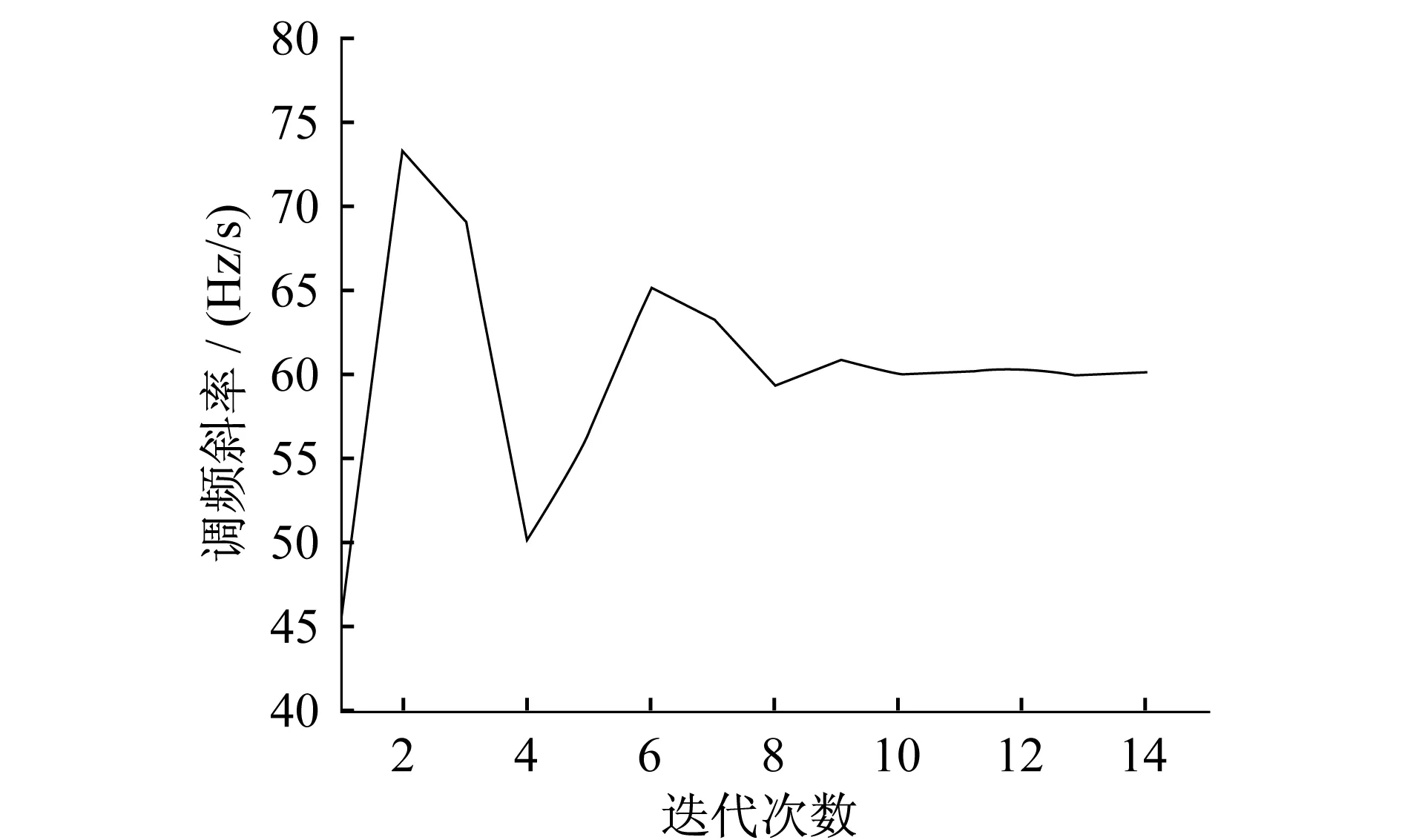
圖3 蟻群算法對調頻斜率估計過程Fig．3 Estimate process of chirp rate with ACO

若信號采樣點數為M，掃描點數為 m，則FRFT算法的復雜度為o( m×M×log M)，掃描點數m由α的步長和范圍確定，其中α的步長取值為0．008［12］，范圍為 10π，則 FRFT 算法的復雜度為:通過上述分析，利用蟻群算法對LFM參數進行估計，能夠在保證估計精度的情況下有效減少計算量，很好地提高了參數估計的效率和質量。

5 結 論

本文在文獻［8］的基礎上，將LFM信號參數估計問題轉化為函數求極值問題，利用蟻群算法全局優化和啟發式尋優的特點，提出了基于蟻群算法的LFM信號參數估計算法。該方法運算量小、參數估計精度高，有效克服了原算法運算量大、不易工程實踐的缺點。

［1］ 王小謨，張光義．雷達與探測［M］．第2版．北京:國防工業出版社，2008．WANG Xiaomo，ZHANG Guangyi．Radar and detection［M］．2nd ed．Beijing:National Defense Industry Press，2008．

［2］ Pace P E，Burton G D．Anit－ship cruise missiles:technology，simulation and ship self－defense［J］．Journal of Electron Defense，1998，21(11):51－ 55．

［3］ Djuric P M，Kay S M．Parameter estimation of chirp signals［J］．IEEE Trans on Acoustics，Speech，and Signal Processing，1990，38(12):2118－2126．

［4］ 陳文武，蔡征宇，陳如山，等．脈沖噪聲下基于Robust STFT的LFM信號檢測與參數估計［J］．南京理工大學學報，2012，12(2):312－329．CHEN Wenwu，CAI Zhengyu，CHEN Rushan，et al．Robust STFT－based detection and parameter estimation of LFM signal in impulsive noise［J］．Journal of Nanjing University of Science and Technology，2012，12(2):312－329．

［5］ Li Yan， Fu Hua， Kam Pooi-Yuen． Improved，approximate，time-domain ML estimators of chirp signal parameters and their performance analysis［J］．IEEE Trans on Signal Processing，2009，57(4):1260－1272．

［6］ Ijima H，Ohsumi A，Djurovic I．Parameter estimation of chirp signals in random noise using wigner distribution［C］∥Proc of the 47th Midwest Symposium on Circuits and Systems．Hiroshima，Japan:［s．n．］，2004:177－180．

［7］ 徐會法，劉鋒，張鑫．分數階Fourier域強弱LFM信號檢測與參數估計［J］．信號處理，2011，27(7):1063－1068．XU Huifa，LIU Feng，ZHANG Xin．Detection and parameter estimation of strong and weak LFM signals in the fractional Fourier domain［J］．Signal Proceessing，2011，27(7):1063－1068．

［8］ 韓孟飛，王永慶，吳嗣亮，等．一種低信噪比下LFM信號參數快速估計算法［J］．北京理工大學學報，2009，29(2):147－151．HAN Mengfei，WANGYongqing，WU Siliang，et al．A fast algorithm on parameter estimation of LFM signals under low SNR ［J］．Transactions of Beijing Institute of Technology，2009，29(2):147－151．

［9］ 朱曉華．雷達信號分析與處理［M］．北京:國防工業出版社，2011．ZHU Xiaohua．Radar signal analysis and processing［M］．Beijing:National Defence Industry Press，2011．

［10］ 楊淑瑩．模式識別與智能計算——MATLAB技術實現［M］．北京:電子工業出版社，2008．YANG Shuying．Pattern recognition and intelligentize count—technology implement of MATLAB［M］．Beijing:Publishing House of Electronics Industry，2008．

［11］ 孫志國，陳晶，申麗然，等．基于TSLPFT1－FFT的線性調頻信號參數估計方法［J］．電路與系統學報，2011，16(5):24－29．SUN Zhiguo，CHEN Jing，SHEN Liran，et al．Parameters estimation of linear frequency modulation signal based on TSLPFT1－ FFT［J］．Journal of Circuits and Systems，2011，16(5):24－29．

［12］ 宋軍，劉渝，朱霞．LFM信號參數估計的插值FRFT算法［J］．系統工程與電子技術，2011，33(10):2189－2194．SONG Jun，LIU Yu，ZHU Xia．Parameters estimation of LFM signals by interpolation based on FRFT［J］．Systems Engineering and Electronics，2011，33(10):2189－2194．