用有限元強度折減法評價海底斜坡穩定性

曹金鳳 曹明君 任 帥

(青島理工大學理學院，山東 青島 266520)

用有限元強度折減法評價海底斜坡穩定性

曹金鳳 曹明君 任 帥

(青島理工大學理學院，山東 青島 266520)

采用基于ABAQUS的有限元強度折減法從三個失穩判據方面對相同有限元模型的陸地斜坡和海底斜坡的塑性應變、等效塑性應變、塑性區發展情況進行了研究，得出了海底斜坡失穩機理和穩定性評價的定量研究依據，為海底斜坡失穩機理和海底地質災害風險評價提供了研究思路。

有限元強度折減法，海底斜坡，穩定性，安全系數，ABAQUS

海底斜坡穩定性的研究成為國內外海洋地質災害研究領域的熱點課題[1,2]。主要原因有兩個：1)海底滑坡能夠破壞工程設施，甚至引發海嘯，造成重大生命財產損失；2)海底蘊含豐富的油氣資源[3]。21世紀初，歐美的科學家針對海底斜坡穩定性進行了一系列專項研究[4]，我國也開展了少量的專項研究。但是，在國內外公開發表的文章中，定量研究和模型研究則比較少見[5]。少量的定量分析中，也多采用極限平衡法或統計方法分析海底斜坡穩定性[6,7]。自1975年Zienkiewicz[8]首次提出有限元強度折減法以來，該法在陸地斜坡的穩定性分析中得到了廣泛的應用[9-11]，但較少應用于海底斜坡穩定性評價。本文將有限元強度折減法引入到海底斜坡穩定性評價和漸進破壞分析中，并對陸地斜坡與海底斜坡的穩定性分析結果進行比較。

1 有限元強度折減法基本理論

有限元強度折減法將強度折減技術與彈塑性有限元方法相結合，在給定的評判指標下，通過不斷調整強度折減系數并對斜坡進行穩定性分析，獲得最小穩定安全系數[12]。

對于摩爾—庫侖材料，折減后的粘聚力和內摩擦角的表達式如式(1)和式(2)所示：

(1)

(2)

其中，c和φ，c′和φ′分別表示折減前/后土的粘聚力和內摩擦角；Fs為強度折減系數，也稱強度儲備安全系數或斜坡穩定安全系數。陸地斜坡的失穩判據主要有4種：1)塑性區貫通；2)等效塑性應變貫通；3)斜坡坡面特征點產生位移突變；4)有限元分析不收斂[13]。

2 有限元模型及參數

2.1 有限元模型

本文基于ABAQUS[15,16]軟件，采用有限元強度折減法評價陸地與海底斜坡的穩定性。斜坡的簡化幾何模型如圖1所示：BC段長300 m，CD段高80 m，ED和AF段分別長70 m和116.94 m，選取海底斜坡極限坡角15°。斜坡底部完全約束；左、右側邊設為對稱邊界 XSYMM(U1=UR2=UR3=0)。選擇單元類型為CPE6，共包含5 049個節點，劃分了2 432個單元；分析過程中啟用Step模塊中的幾何非線性開關和非對稱求解器。

2.2 陸地斜坡與海底斜坡土的物理力學參數

為了比較陸地滑坡與海底滑坡的不同，本文均選取粉質粘土斜坡作為研究對象，參數如表1所示[13,14]。

表1 土的物理力學參數

本文選取非關聯流動法則，假定陸地斜坡剪脹角取值13°。根據淺地層靜力觸探資料統計分析結果，粉質粘土的粘聚力取值范圍為2 kPa～25 kPa，摩擦角的取值范圍為0.5°～5.4°，本文取相同的粘聚力c=10 kPa，摩擦角取5°，剪脹角假定為1.5°。海底斜坡穩定性分析過程中，選取浮容重10 kN/m3作為自重荷載。

3 陸地斜坡穩定性結果分析

本文對陸地斜坡穩定性進行評價時，選取塑性區貫通、等效塑性應變貫通和有限元分析不收斂3種失穩判據(為敘述方便，3種失穩判據依次用①，②，③表示)得到的穩定性安全系數分別為1.82，1.83和1.9，分析結果詳細過程如下。

3.1 塑性應變εp

圖2為當Fs=1.82時塑性區的發展情況：第2幀時在坡腳位置F處首先出現塑性應變，隨后塑性區逐漸向坡頂E延伸(見圖2b)，圖2c))，分析結束時塑性區貫通。

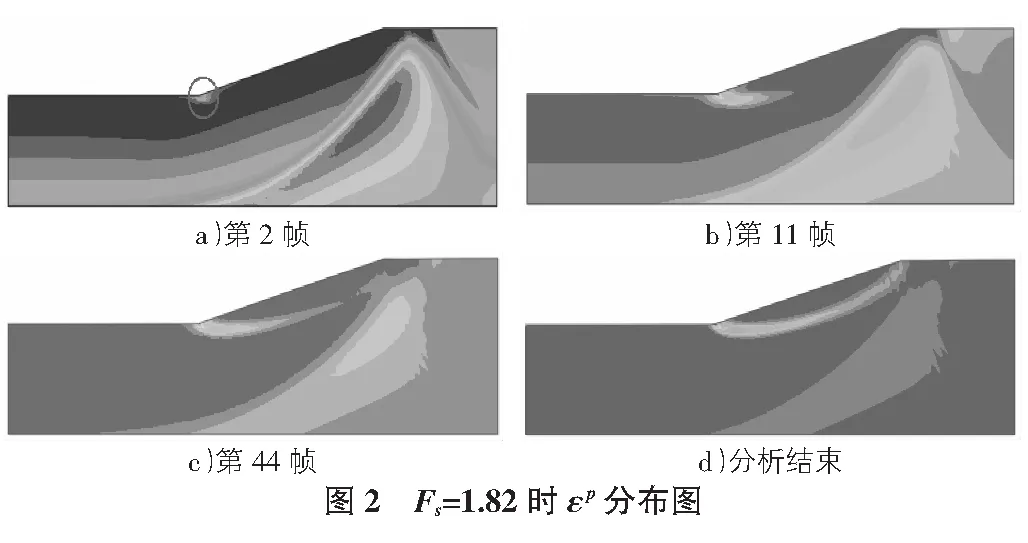
3.2 等效塑性應變εpe

失穩判據②的穩定安全系數為1.83(見圖3)，εpe的變化趨勢與εp類似，它首先出現在坡腳F處，然后逐漸向E延伸，分析結束時刻等效塑性應變區域貫通。

表2給出3種失穩判據得到的穩定安全系數比較情況：失穩判據①和②之間的誤差僅為0.55%，失穩判據③的安全系數誤差為3.83%。

表2 陸地斜坡穩定安全系數比較

3.3 不同折減系數時塑性區發展情況

為了看出不同折減系數對εp影響，圖4中給出了失穩判據①時εp的發展情況。從圖4中可以看出：Fs=1.2時首先在F處出現塑性應變，隨著折減系數的不斷增加，逐漸向E處延伸，當塑性區貫通時，即為失穩判據①，當折減系數進一步增加時，等效塑性應變區域貫通，進而有限元分析不再收斂。

4 海底斜坡穩定性結果分析

對于海底斜坡，失穩判據①，②，③對應的安全系數分別為1.205，1.215和2.8。分析結果詳細介紹如下。

4.1 塑性應變εp

圖5為當Fs=1.205時塑性應變的發展情況：第3幀時在F處首先出現εp；然后第5幀在F的左側區域也出現εp；第7幀時在G處可以觀察到明顯的塑性區，隨后塑性區從G處開始逐漸向坡頂E的右側方向延伸(見圖5c))，分析結束時塑性區貫通。

4.2 等效塑性應變εpe

圖6為當Fs=1.215時εpe的發展情況：第5幀在F處首先出現εpe；然后很快在F左下側G處也出現εpe(見圖6b))；隨后從G位置逐漸向E的右側方向延伸(見圖6c))；分析結束時等效塑性應變區域貫通(見圖6d))。

表3給出了穩定安全系數的比較情況：判據①和②之間的誤差為0.82%。判據③得到的結果誤差達到130.45%。

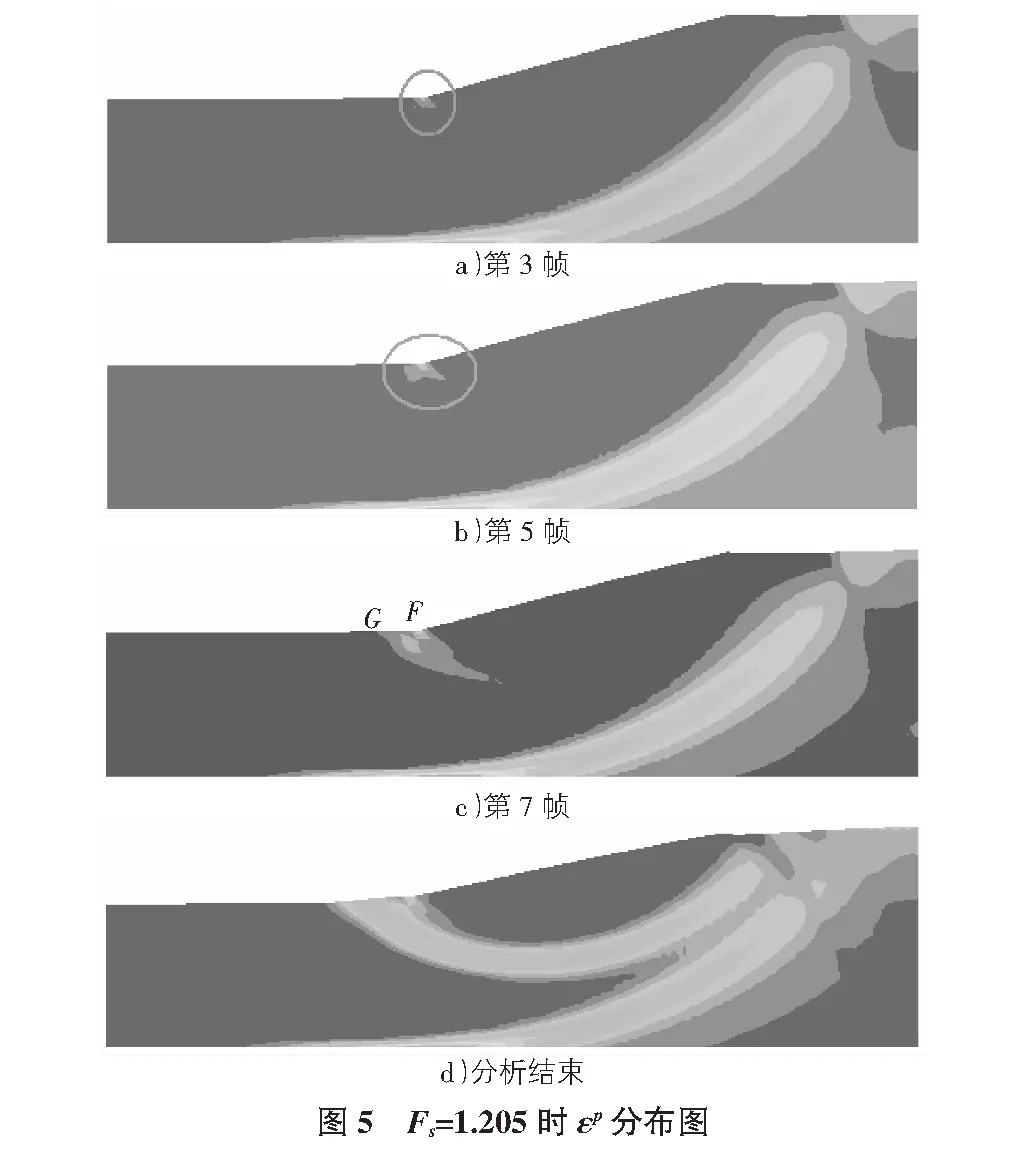
表3 海底斜坡穩定安全系數比較

4.3 不同折減系數時塑性區發展情況

從圖7中可以看出：Fs=1.0時在F處已經出現了εp，且影響范圍向A側擴展(見圖7a))；Fs=1.1時，塑性區范圍擴大，隨著折減系數的不斷增加，逐漸向坡頂E的右側延伸，坡頂E、坡腳F附近區域出現明顯的“塌陷”和“隆起”現象(見圖7c)，圖7d))；如果Fs繼續增加，塑性區分別向A，D附近擴展(見圖7e))；有限元分析不收斂時，塑性區的影響范圍是整個斜坡(見圖7f))。

5 結果比較

5.1 穩定安全系數

比較表2和表3：對于陸地斜坡和海底斜坡，失穩判據①和②得到的穩定安全系數接近，誤差分別為0.55%和0.82%，滿足工程上允許的誤差要求；對于陸地斜坡，失穩判據③得到的安全系數值為3.83%，也能夠滿足工程上允許的誤差范圍，但是海底斜坡的誤差達到130.45%，該失穩判據能否應用于海底斜坡的穩定性評價，值得進一步研究。

5.2εp，εpe的出現位置和影響范圍

1)出現位置。比較圖2與圖5、圖3與圖6可知：無論是陸地斜坡還是海底斜坡，εp和εpe均首先出現在坡腳F處，但是前者不向A側擴展，隨著折減系數的增加，將逐漸向坡頂E處延伸，直至失穩判據①，②，③依次出現；而對于后者，坡腳F處出現εp和εpe后，瞬時向靠近A側方向擴展，隨著折減系數的不斷增加，F處的εp和εpe值幾乎無變化，而是從G處向坡頂E右側逐漸貫通。

2)影響范圍。比較圖2d)與圖5d)，圖3d)與圖6d)可知：陸地滑坡的滑動剪切帶更窄、更淺，影響范圍更小；而海底滑坡的滑動剪切帶更寬、更深，影響范圍更大。對于失穩判據①，②，③，陸地滑坡的塑性區和等效塑性應變區的影響范圍分別為16.25 m，16.74 m，18.21 m；海底滑坡的影響范圍分別為37.4 m和38.8 m，60 m(斜坡高度)，是陸地斜坡影響范圍的2倍左右。

6 結論與討論

本文得出下列主要結論：

1)對于失穩判據①，②，陸地斜坡的穩定安全系數分別為1.82，1.83，均大于海底斜坡的穩定安全系數1.205,1.215,對于失穩判據③，陸地的穩定安全系數為1.9，小于海底的2.8。2)失穩判據①和②適用于陸地斜坡和海底斜坡穩定性評價，失穩判據③適用于陸地斜坡穩定性評價，在海底斜坡穩定性評價中是否適用值得商榷。3)海底斜坡的εp和εpe首先出現在坡腳F處，但很快會向靠近A側擴展，并從該位置向坡頂E右側延伸；陸地斜坡的εp和εpe首先出現在坡腳F處，并從該位置逐漸延伸至坡頂E處。4)陸地滑坡的滑動剪切帶更窄、更淺、邊界更清晰、影響范圍更小；而海底滑坡的滑動剪切帶則更寬、更深、邊界更不清晰、影響范圍更大。5)海底滑坡時坡腳F和坡頂E附近區域出現明顯的“隆起”和“塌陷”現象，符合“塌陷、滑動”型滑坡[5]；而陸地滑坡則不出現或出現少量“隆起”，屬于剪切型滑坡。6)本文介紹的方法可以根據海底土的力學參數、地層信息，給出關心區域的穩定性安全系數，為復雜海底滑坡的失穩機理研究提供了一種新思路。

[1] Henry S，Pettingill，Paul Weimer.Worldwide deep water exploration and production：Past，present and future[J].The Leading Edge，2002，21(4)：371-376.

[2] 張功成，米立軍，吳時國，等.深水區—南海北部大陸邊緣盆地油氣勘探新領域[J].石油學報，2007，28(2)：15-21.

[3] 陸紅鋒，孫曉明，張 美.南海天然氣水合物沉積物礦物學和地球化學[M].北京：科學出版社，2011.

[4] LOCAT J，Lee H J.Submarine landslides：Advances and challenges[J].Canadian Geotechnical Journal，2002(39):193-212.

[5] 胡光海，劉振夏，房俊偉，等.國內外海底斜坡穩定性研究概況[J].海洋科學進展，2006，24(1)：130-136.

[6] 張 亮，欒錫武.南海北部陸坡穩定性定量分析[J].地球物理學進展，2012，27(4):1443-1453.

[7] 楊春霞,王春民,王圣潔.南海北部災害地質穩定度評價模型[J].中國地質災害與防治學報,2006,17(1):77-79.

[8] Zienkiewicz O C，Humpheson C，Lewis R W.Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geostechnique,1975,25(4):671-689.

[9] Griffith D V，Lane P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3):387-403.

[10] Dawson E M，Roth W H，Drescher A.Slope stability analysis by strength reduction[J].Geotechnique，1999，49(6)：835-840.

[11] 趙尚毅，鄭穎人，時為民，等.用有限元強度折減法求邊坡穩定安全系數[J].巖土工程學報，2002，24(3)：343-346.

[12] MANZARI M T，NOUR M A.Significance of soil dilatancy in slope stability analysis[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(1):75-80.

[13] 萬少石，年廷凱，蔣景彩，等.邊坡穩定強度折減有限元分析中的若干問題討論[J].巖土力學，2010，31(7)：2283-2288.

[14] 崔可銳，毛由田.巖土工程師實用手冊[M].北京：化學工業出版社，2007.

[15] 曹金鳳，王旭春，孔 亮.Python 語言在 Abaqus 中的應用[M].北京：機械工業出版社，2011.

[16] 曹金鳳，石亦平.ABAQUS有限元分析——常見問題解答[M].北京：機械工業出版社，2009.

Evaluation on submarine slope stability with strength reduction FEM

Cao Jinfeng Cao Mingjun Ren Shuai

(CollegeofTechnology,QingdaoUniversityofTechnology,Qingdao266520,China)

The paper studies plastic strain, equivalent plastic strain and plastic zones development conditions of land slope and ocean slope with similar finite element models from three instability data by applying strength reduction FEM on the basis of ABAQUS, and obtains quantitative research basis of ocean slope instability mechanism and stability evaluation, which has provide some concepts for ocean slope instability mechanism and submarine geology disaster risk evaluation as well.

strength reduction FEM, submarine slope, stability, safety coefficient, ABAQUS

2015-08-26

曹金鳳(1978- )，女，博士，副教授； 曹明君(1990- )，男，在讀碩士； 任 帥(1988- )，男，在讀碩士

1009-6825(2015)31-0049-04

TU413.62

A