關于部分變元強穩定性的幾個定理

劉丹

(山東科技大學數學與系統科學學院，山東青島266590)

關于部分變元強穩定性的幾個定理

劉丹

(山東科技大學數學與系統科學學院，山東青島266590)

本文給出了微分系統關于部分變元的強漸進穩定及在持續攝動下強漸進穩定的幾個定理，改進和推廣了已有文獻的相關結果.

部分變元;強漸近穩定;持續攝動;強一致穩定

1 引言

眾所周知，Liapunov直接法是研究系統穩定性的一個十分有效的方法.目前，圍繞Liapunov意義下的穩定性、部分變元的穩定性的結果比較豐富，如文獻［1－5］.然而近幾十年來，人們根據實際情況的需求提出了關于部分變元的強穩定性的概念.運用Liapunov直接法研究部分變元的強穩定性的成果還不夠豐富.本文將借鑒文獻［6－9］的基本思想，討論部分變元的強漸進穩定、強一致漸進穩定，并推廣到有擾動項的持續攝動下關于部分變元的強一致穩定和強漸進穩定.

2 定義與引理

考慮n維非自治系統

其中x∈Rn，f(t，x)∈C［I×Ω，Rn］，I=［0，+∞)，Ω為開區域，f(t，0)≡0.記

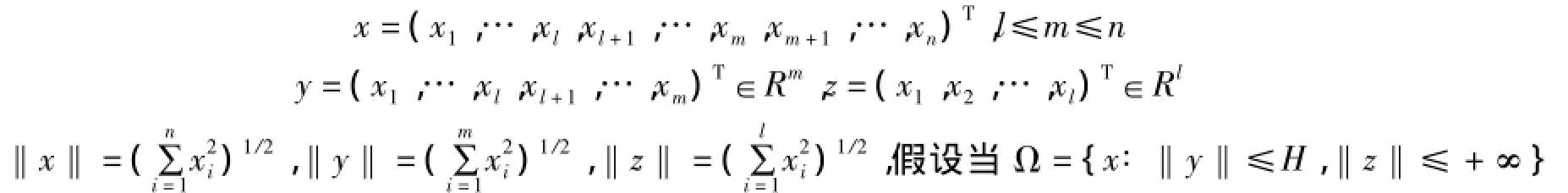
時，(1)的解唯一且可延拓到I上.

對于(1)式的擾動系統

其中R(t，x)∈C［I×Ω，Rn］，R(t，0)=0，R(t，0)不恒為零.

定義1［1］稱(1)的平凡解關于部分變元z對y強穩定，如果對于任何ε＞0和t0∈I，存在δ(ε，t0)＞0，使得當x0滿足‖y0‖≤δ(ε)時，對一切t≥t0，有‖z(t，t0，x0)‖≤ε.

定義2［1］稱(1)的平凡解關于部分變元z對y強一致穩定，如果對于任何ε＞0，存在δ(ε)＞0，使得當x0滿足‖y0‖≤δ(ε，t0)時，對一切t0∈I，當t≥t0時有‖z(t，t0，x0)‖≤ε.

定義3［1］稱(1)的平凡解關于部分變元z對y強吸引的，如果對于任意ε＞0及t0∈I，存在δ(t0)＞0，使得當x0滿足‖y0‖≤δ時，存在T(ε，t0，x0)＞0，當t≥t0+T(ε，t0，x0)時有‖z(t，t0，x0)‖＜ε，即

定義4［2］稱(1)的平凡解關于部分變元z對y強漸近穩定的，若(1)的平凡解關于部分變元z對y是強穩定的且z對y是強吸引的.

定義5［1］稱(1)的平凡解關于部分變元z對y強等度漸近穩定的，若(1)的平凡解關于部分變元z對y是強穩定，且對任意ε＞0及t0∈I，存在δ(t0)＞0及T(ε，t0)＞0，使得當x0滿足‖y0‖≤δ時，對t≥t0+T(ε，t0)時有‖z(t，t0，x0)‖＜ε.

定義6［1］稱(1)的平凡解關于部分變元z對y強一致漸近穩定的，若(1)的平凡解關于部分變元z對y是強一致穩定，且δ＞0，對任意ε＞0及t0∈I，存在T(ε，δ)＞0，使得當x0滿足‖y0‖≤δ時，對t≥t0+T(ε，δ)時有‖z(t，t0，x0)‖＜ε.

定義7［1］對于連續函數V(t，x)=V(t，y，z)，若有V(t，0，z)≡0，則稱V(t，x)為推廣的Liapunov函數或y－V函數.

定義8稱式(1)的平凡解在每時刻很小的經干擾下關于部分變元z對y強一致穩定，若對且任意的ε＞0及t0∈I，存在δ1(ε)＞0和δ2(ε)＞0，使滿足當‖y0‖＜δ1(ε)與‖R(t，x)‖＜δ2(ε)時，對t≥t0，有‖z(t，t0，x0)‖＜ε.

定義9稱式(1)的平凡解在每時刻很小的經干擾下關于部分變元z對y強吸引，若對且任意的ε＞0及t0∈I，存在δ(t0)＞0和T(ε)＞0，使滿足當‖y0‖＜δ(t0)，對t≥t0+T，有‖z(t，t0，x0)‖＜ε.

引理［1］若存在y－V函數V(t，x)滿足:(1)φ(‖z‖)≤V(t，x)φ∈K;(2)D+V|(1)≤0)，稱式(1)的平凡解關于部分變元z對y是強穩定的.

3 主要結果

定理1存在y－V函數V(t，x)滿足:

(1)φ1(‖z‖)≤V(t，x)，φ1∈K，

(2)D+V|(1)≤－g(t)φ2(‖y‖)，φ2∈K，其中g(t)≥0且

則系統(1)平凡解關于部分變元z對y強漸近穩定.

證明由引理可知，式(1)的平凡解關于部分變元z對y是強穩定的.下面證明(1)平凡解關于部分變元z對y是強吸引的，即有?ε＞0，存在δ(t0)＞0，使得當‖y0‖≤δ(ε，t0)時，有y0，z0))=V∞＞0.

從而φ1(‖z‖)≤V(t，x(t，t0，y0，z0))→0(t→+∞)，‖z‖→0(t→+∞).

若不然，則存在t0∈I，?δ＞0，當‖y0‖≤δ時，有

由條件(2)可知D+V|(1)＜0，故有tlim+V(t，x(t，t0，y0，z0))△=V∞.

→∞

從而V(t，x(t，t0，y0，z0))≥V∞＞0，利用條件(1)和(2)可知，D+V|(1)≤－g(t)φ3(φ－12(V∞)).

故可得到0≤V(t，x(t，t0，y0，z0))≤V(t0，y0，z0)－φ3(δ(ε))

而當t?t0時上式不成立.于是

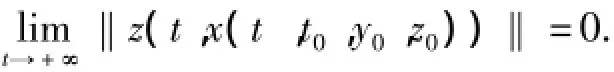
證得系統(1)平凡解關于部分變元z對y強漸近穩定.

定理2存在y－V函數V(t，x)滿足:

(1)φ1(‖z‖)≤V(t，x)≤φ2(‖y‖)，φi∈K(i=1，2，3)，

(2)D+V|(1)≤－g(t)φ3(‖y‖)，其中g(t)≥0且對于?B＞0都存在b＞0使得系統(1)平凡解關于部分變元z對y強一致漸近穩定.

證明先證明系統(1)平凡解關于部分變元z對y強一致穩定性.

對?ε＞0，取δ(ε)=φ－12(φ1(ε))，當‖y0‖＜δ(ε)時，由已知條件有

φ1(‖z(t，t0，x0)‖)≤V(t，x(t，t0，y0，z0))≤V(t0，y0，z0)≤φ2(‖y(t，t0，x0)‖)＜φ1(ε)，即‖z(t，t0，x0)‖＜ε.

下證系統(1)強一致吸引性，對?ε＞0，存在△0＞0，使得當‖y0‖≤△0時，?T(ε)＞0，當t≥t0+ T(ε)時，有‖z(t，t0，x0)‖≤ε.

設對于△0=δ(H)，當‖y0‖≤△0，取有已知條件(2)，存在T＞0，當任意t0∈I有則一定存在t1∈［t0，t0+T］，使‖y0(t1，t0，y0，z0)‖≤δ(ε).

若不然，?t∈［t0，t0+T］有‖y0(t1，t0，y0，z0)‖≥δ(ε)，由已知條件(2)有D+V|(1)≤－g(t)φ3(δ (ε))，即

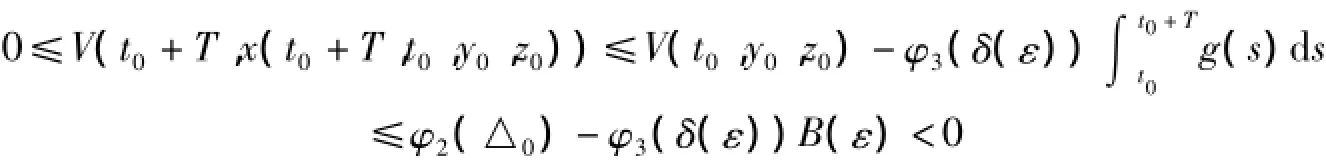
這與V(t，x)正定矛盾.

因此，存在t1∈［t0，t0+T］使‖y0(t1，t0，y0，z0)‖≥δ(ε)，從而有

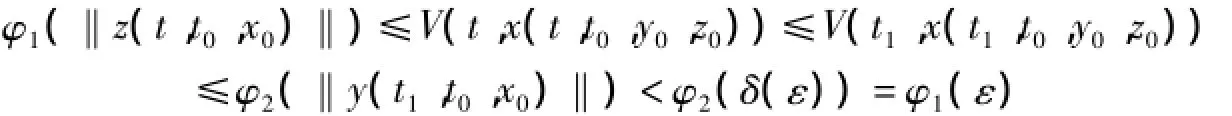
即當t≥t0+T時，有‖z(t，t0，x0)‖≤ε.證得系統(1)平凡解關于部分變元z對y強一致吸引.

綜上可得，系統(1)平凡解關于部分變元z對y強一致漸近穩定性.

推論1存在y－V函數V(t，x)滿足:

(1)φ1(‖z‖)≤V(t，x)≤φ2(‖y‖)，φi∈K(i=1，2，3)，

(2)D+V|(1)≤－g(t)φ3(‖y‖)，其中g(t)≥0且

則系統(1)平凡解關于部分變元z對y強等度漸近穩定.

證明由條件(1)和(2)可表示為D+V|(1)≤－g(t)φ3(φ－12(V(t，x)))

證明過程與定理2的方法類似，此定理顯然是成立的.

定理3存在y－V函數V(t，x)滿足:

(2)φ1(‖z‖)≤V(t，x)≤φ2(‖y‖)，φi∈K(i=1，2，3);

(3)D+V|(1)≤－g(t)φ3(‖y‖).

則有式(1)平凡解在每時刻很小的經干擾下關于部分變元z對y強一致穩定.

證明由條件(2)有‖y‖≥φ－12(V(t，x)).由條件(3)

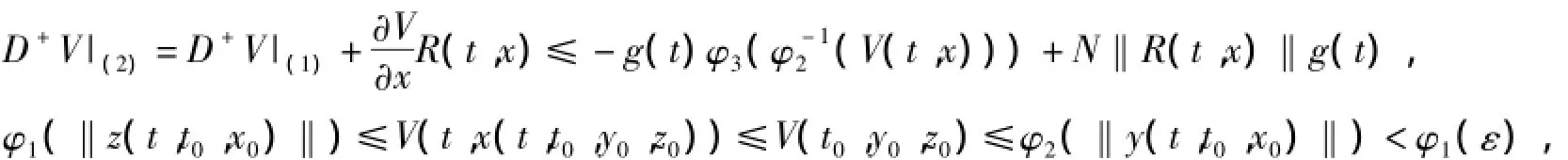
即‖z(t，t0，x0)‖＜ε.

對?ε＞0，‖R(t，x)‖＜δ2(ε)時，由條件(3)知D+V|(1)＜0.當‖y0‖＜δ1(ε)時，有V(t0，y0，z0)≤φ1(‖ε‖).

需證t≥t0，V(t，x(t，t0，y0，z0))＜φ1(‖ε‖).

若不然，則存在t1∈I使V(t1，x(t1，t0，y0，z0))=φ1(‖ε‖)，于是?t'0∈(t0，t1)使

這與D+V|(1)＜0矛盾.從而有φ1(‖z(t，t0，x0)‖)≤V(t，x(t，t0，y0，z0))≤φ1(‖ε‖).

即‖z(t，t0，x0)‖＜ε(t≥t0)，式(1)平凡解在每時刻很小的經干擾下關于部分變元z對y強一致穩定.

證明對定理3中的條件(2)的解有

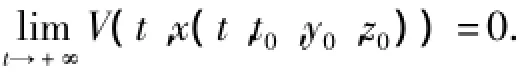
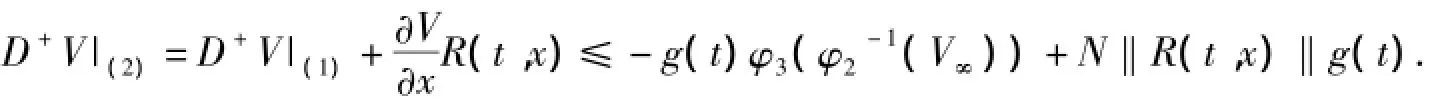
取T1＞T，當t≥t0+T1時有‖R(t，x)‖≤r≤φ3(φ2－1(V∞))/N.

因此D+V|(2)≤－g(t)φ3(φ2－1(V∞))+Nrg(t).

［1］廖曉昕.穩定性的數學理論與應用［M］.武漢:華中師范大學出版社，1988.

［2］蹇繼貴，萬新敏.關于微分方程部分變遠漸近穩定性定理的改進［J］.空軍雷達學院學報，2003(4):46－47.

［3］馮濱魯.Liapunov穩定性定理的推廣［J］.系統科學與數學，1998(2):211－214.

［4］徐道義，顏祥偉.關于部分變元漸近穩定性的幾個基本定理［J］.四川師范大學學報(自然科學版)，1996(2):6－11.

［5］馮濱魯.穩定性定理的推廣［J］.山東師范大學學報(自然科學版)，1992(2):16－19.

［6］周康.關于部分變元的強穩定性的基本定理［J］.華中師范大學學報(自然科學版)，1995(1):24－26.

［7］孟新柱.部分變元的強穩定性研究［J］.山東科技大學學報(自然科學版)，2002(3):18－20.

［8］張維.微分系統關于部分變元的強穩定性［J］.華中師范大學學報(自然科學版)，1992(4):17－21.

［9］劉丹.關于部分變元的強穩定性［J］.濰坊學院學報，2015(2):14－16.

Several Theorems of Strong Stability on Partial Variables

LIU Dan
(School of Mathematics and Systems Science，Shandong University of Science and Technology，Qingdao，266590，China)

The several theorems are given with respect to partial uniformly asymptotic stability and partial asymptotic stability under continuous perturbation，which improves and generalizes the existing conclusions in relevant literatures.

partial variables;strong asymptotic stability;continuous perturbation;strong uniformly stability

O175.21

A

1672－2590(2015)06－0030－04

2015－09－17

劉丹(1991－)，女，黑龍江方正人，山東科技大學數學與系統科學學院碩士研究生.