激勵函數可學習神經網絡

楊少明，王雅琳，王美蘊，何海明，李勇剛

(中南大學信息科學與工程學院，湖南長沙 410083)

激勵函數可學習神經網絡

楊少明，王雅琳*，王美蘊，何海明，李勇剛

(中南大學信息科學與工程學院，湖南長沙 410083)

提出了一種激勵函數可學習神經網絡，其神經元函數不固定，通常是任何線性無關的基函數的線性組合，通過調整神經元中基函數的系數即可達到網絡學習的目的。為了結構優化方便，將神經元輸出的多維空間映射為一維空間后輸入給下層神經元。根據網絡的特點，提出了兩種無需迭代的網絡參數快速學習算法實現網絡訓練。通過3個實例進行仿真實驗，結果表明所設計神經網絡的逼近能力強，參數學習速度極快。

神經網絡;激勵函數;快速學習方法

神經網絡尤其是BP神經網絡由于其結構簡單、并行處理能力強、非線性逼近能力好等特點，已經廣泛應用于各種領域。但是，BP算法是采用非線性規劃的快速下降法，即沿著誤差函數的負梯度方向修改權值，因此存在學習效率低、收斂速度過慢和容易陷入局部最優等問題。針對BP神經網絡算法的缺陷，許多研究人員在學習率的改進［1-3］;網絡初始權值選取的改進［4-5］;網絡模型結構的優化［6-8］;進化算法優化網絡參數和結構［9-11］以及其他方面［12-16］做了大量的研究工作。

泛函網絡［17-18］是Enrique Castillo于1998年提出的一種網絡，是對標準神經網絡的推廣。泛函網絡是基于泛函方程的，并且是一種參數化建模方法。泛函網絡的建立需要根據專業領域的知識去衍生各種泛函方程，從而對泛函網絡的模型進行有根據的假設。泛函網絡處理的是一般泛函模型，神經元之間無權值連接，神經元函數可以是多元的，通常是給定基函數簇的線性組合，且神經元函數不是固定的，是可學習的。泛函網絡已經成功應用于線性與非線性回歸、非線性系統辨識、微分、差分方程的求解等問題。泛函網絡不僅可以解決神經網絡可以解決的問題，還能處理神經網絡無法解決的問題，泛函網絡在某些方面是優于神經網絡的［18］。

泛函網絡在黑箱建模時，與神經網絡一樣，存在著網絡結構確定困難的問題。在絕大部分情況下，初始給定的網絡結構都不是最合理的，需要在網絡完全學習或是部分學習之后優化網絡的結構。如果網絡結構有冗余或者是達不到預期的精度，那么在結構優化時需要根據網絡的學習情況適度刪減或者增加神經元的個數等。對于一般的泛函網絡而言，其神經元函數的輸入參數是一個多維向量，這就表明，它的網絡結構在刪減時勢必會出現一些不可避免的問題。如上一層神經元的刪除，會直接影響下一層神經元的輸入向量的維數，造成與神經元函數不匹配，給網絡運行造成困難。

針對這個問題，文中提出了一種激勵函數可學習神經網絡(簡稱可學習神經網絡)，把泛函神經元輸出的多維空間映射至一維空間后輸入給下一層的神經元，并采用帶偏置的線性組合形式表示這種映射關系。針對新設計的網絡，文中給出了兩種網絡參數學習算法，并通過實例驗證了網絡的可行性與有效性。其中，學習算法二引用黃廣斌等［14］提出的極限學習機(ELM)算法［13-16］，不同的是，ELM算法中隱層激勵函數單一固定，而文中提出的可學習神經網絡，隱層激勵函數的種類和數量都不固定，可學習調整。經實驗仿真，所提網絡與ELM相比學習速度相近，擬合效果更好。

1 激勵函數可學習神經網絡

1.1 神經元模型

激勵函數可學習神經網絡的神經元函數是任意線性無關的基函數簇的線性組合，每個神經元的輸入都是上一層網絡神經元(或者輸入節點)所有輸出的線性累加和，每個神經元(或者輸入節點)的輸出都是下一層神經元的輸入(或者是網絡模型的輸出)。其神經元模型如圖1所示。

X=［x1，x2，…，xn］是神經元的輸入，y是神經元的輸出:

神經元函數f可以是任意非線性相關基函數的線性組合:

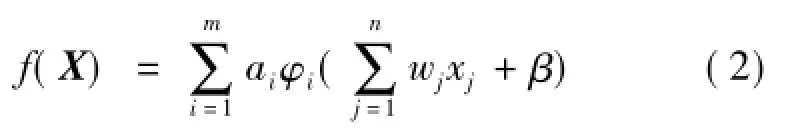
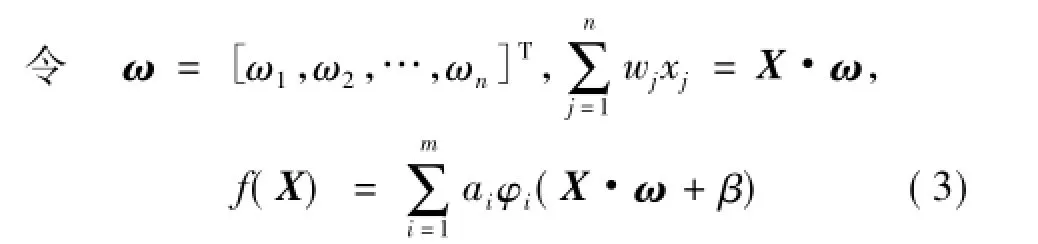
其中，ω和β為隨機選擇的神經元參數，無需調整; {φ1，φ2，…，φm}為任意的基函數簇，如三角函數簇{sin(x)，sin(2x)，sin(3x)，…}，對數函數簇{ln|x|+1，ln|x|+2，ln|x|+3，…}，多項式函數簇{1，x，x2，x3，…}等，也可以是混合函數簇，如{sin(x)，cos(x)，ex，ln(|x|+1)，sinh(x)，…}。通常是根據實際問題選擇合適的函數簇，并在網絡學習的過程中，根據學習情況，不斷進行調整。ai(i= 1，2，…，m)為網絡的參數，主要是通過對它們的學習實現對網絡的逼近，達到期望的精度。

圖1 激勵函數可學習神經網絡神經元模型Fig.1 Neuron model of the active function learning neural network

1.2 網絡的一般模型

激勵函數可學習神經網絡的一般網絡模型如圖2所示。

圖2 激勵函數可學習神經網絡一般模型Fig.2 Generalmodel of the active function learning neural netw ork

該網絡模型由k個輸入，h個輸出，一個輸入層，d個隱層，一個輸出層。輸入層k個節點，節點的主要功能是輸入信息;隱層和輸出層神經元都是任意線性無關基函數的線性組合。

模型輸入為X=［x1，x2，…，xk］，輸出為Y=［y1，y2，…，yh］，隱層i(i=d+1時表示輸出層)的神經元個數是pi，第j個神經元的函數為fi，j，輸入為xi，j，輸出為zi，j，基函數個數為mi，權值矩陣為ωi，j，偏置為βi，j。

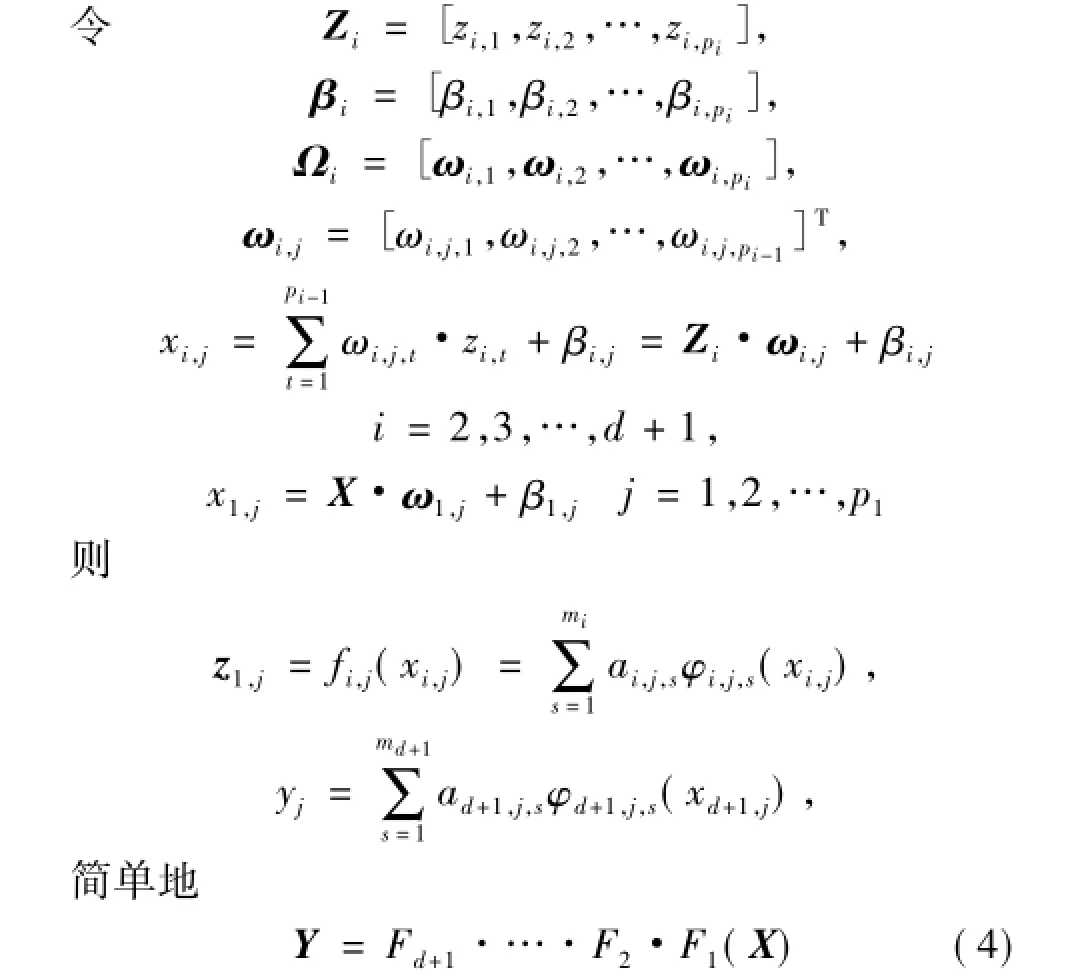
1.3 網絡的學習算法

以輸入為X=［x1，x2，…，xk］，輸出為y的多輸入單輸出單隱層激勵函數可學習神經網絡為例，網絡模型如圖3所示。

圖3 多輸入單輸出網絡模型Fig.3 Mu ltip le input single output network model

隱層有p個神經元，第i個神經元函數是fi，fi是可以學習的，通常表示為一系列基函數的線性組合:

其中:m為神經元基函數的個數，

si=X·ωi+βi，ωi=［ωi，1，ωi，2，…，ωi，k］T。

輸出神經元的函數存在逆函數時也可以表示為基函數的線性組合:

則模型的輸出為

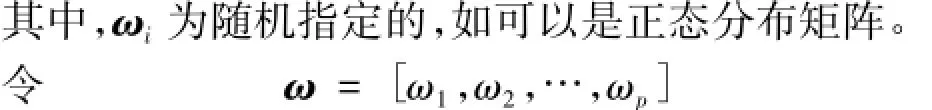
容易知道，在輸出神經元函數給定且存在逆函數時，其隱層參數矩陣A可以通過求解隱層神經元輸出矩陣的廣義逆得到。這種學習算法具有簡單、無需迭代、精度好等特點。

2 應用實例

2.1 實例1

Hénon混沌系統為

用圖5所示的網絡(模型隱層神經元個數為p)對100組Hénon序列進行學習，學習結束后再用100組序列做預測。網絡隱層權值和偏置是按正態分布隨機選擇的，神經元函數的選擇、訓練誤差和測試誤差見表1(文中誤差均指均方根誤差)。

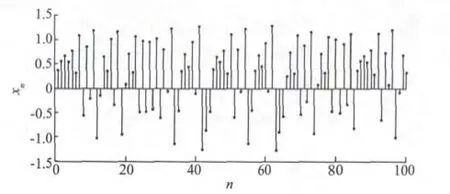
圖4 Hénon混沌序列Fig.4 Hénon Chaotic sequence

圖5 Hénon序列的網絡學習Fig.5 Learning on the Hénon sequence

表1 對Hénon序列學習的網絡模型參數和學習情況Tab.1 Netw ork model param eters and learning on the Hénon sequence

由表1可知，文所提出的激勵函數可學習神經網絡神經元基函數序列不同時對樣本的學習能力是不同的，可以通過改變神經元的基函數類型提高網絡的精度。神經元基函數序列選取合適的話，網絡的逼近效果會提高很多。

2.2 實例2

對于函數

在自變量x∈［－20，20］范圍內，隨機選取1 000個樣本點，其中500個作為訓練數據，另外500個作為測試數據。用圖5所示的激勵函數可學習神經網絡逼近sinc函數，結果見表2。

表2 對sinc函數學習的網絡模型參數和學習情況Tab.2 Network m odel parameters and learning on the sinc function

由表2可知，文中所提的激勵函數可學習神經網絡對sinc函數的學習精度很高，完全可以滿足精度要求，且不同基函數序列對sinc函數的學習情況也是有很大差別的。

在中國綜合國力日益強大、海外投資逐年增長的大趨勢下，中國不應當擔心賦予公司雙重國籍可能引起的更多外交保護壓力。若中國仍持上述保守立場，會阻礙中國向開拓國際市場的中國公司實施外交保護。

分別用文中單隱層激勵函數可學習神經網絡和基于ELM算法的單隱層神經網絡逼近sinc函數。其中，兩種網絡的隱層神經元的權值和閾值均是隨機選取且相等的。

1)可學習神經網絡神經元基函數序列取

{sin(x+1)，sin(2x+2)，sin(3x+3)}，基于ELM方法的單隱層神經網絡的激勵函數取Sigmoid函數

網絡學習情況見表3。

表3 兩種網絡模型對sinc函數學習情況1Tab.3 First learning of two d ifferent netw orks on the sinc function

2)可學習神經網絡神經元基函數序列取

{(1+e－0.25x)－1，(1+e－0.5x)－1，(1+e－0.75x)－1}，基于ELM方法的單隱層神經網絡的激勵函數取Sigmoid函數

學習情況見表4所示。

表4 兩種網絡模型對sinc函數學習情況2Tab.4 Second learning of two different networks on the sinc function

2.3 實例3

分別比較了兩種網絡在兩個實際問題數據集的表現(被比較的兩個網絡隱層權值和偏置均是隨機選取的且相等)。

2.3.1 對Abalone問題的學習

1)可學習神經網絡的激勵函數序列為

ELM網絡的激勵函數取Sigmoid函數

學習情況如表5所示。

表5 兩種網絡模型的對Abalone問題的學習情況1Tab.5 First learning of two different networks on the Abalone p roblem

2)可學習神經網絡的激勵函數序列為

學習情況如表6所示。

2.3.2 對Machine CPU問題的學習

1)可學習神經網絡的激勵函數序列為

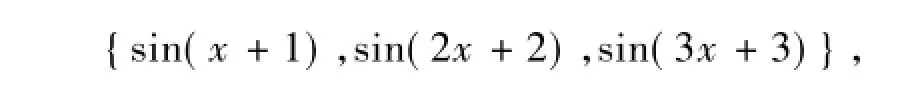
ELM網絡的激勵函數取Sigmoid函數

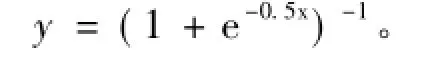
學習情況見表7。

表6 兩種網絡模型對Abalone問題的學習情況2Tab.6 Second learning of two differen t networks on the Abalone p rob lem

表7 兩種網絡模型的對M achine CPU問題的學習情況1Tab.7 First learning of tw o d ifferent networks on the M achine CPU p roblem

2)可學習神經網絡的激勵函數序列為

ELM網絡的激勵函數取Sigmoid函數

學習情況見表8。由表3～表8可知，在網絡固定參數(隱層神經元個數、權值和偏置)隨機選取且相等的情況下，與ELM一樣，參數學習都不需要迭代，速度非常快，但是學習精度要比ELM高。

表8 兩種網絡模型的對M achine CPU問題的學習情況2Tab.8 Second learning of two d ifferen t networks on the M achine CPU p roblem

3 結語

文中在分析了神經網絡和泛函網絡各自的特點基礎上，提出了一種激勵函數可學習的神經網絡，通過改變神經元函數，使網絡參數學習快、結構優化方便。由仿真結果可知，所提網絡的逼近能力強，且由于參數學習無需迭代，大大節省了網絡學習的時間。另外，在神經元個數相同且隱層參數均隨機選擇且相等的情況下，所提激勵函數可學習神經網絡與ELM相比，參數學習速度相近，但是逼近能力更強。

值得提出的是，文中提出這個網絡模型是為了方便模型結構的優化，后續研究將進一步探討如何實現激勵函數可學習神經網絡的修剪式結構優化。

［1］Sin-Chun Ng，Chi-Chung Cheung，Shu-hung Leung.Magnified gradient function with deterministic weightmodification in adaptive learning［J］.IEEE Transactions on Neural Networks，2004，15(6):1411-1423.

［2］Zweiri Y H，Whidborne J F，Althoefer K，et al.A new three-term backpropagation algorithm with convergence analysis［C］// Proceedings of ICRA＇02.IEEE International Conference on Robotics and Automation.Washington DC:IEEE，2002，4:3882-3887.

［3］Zweiri Y H，Seneviratne L D，Althoefer K.Stability analysis of a three-term backpropagation algorithm［J］.Neural Networks，2005，18(10):1341-1347.

［4］Jim Y F Yam，Tommy W SChow.A weight initialization method for improving training speed in feedforward neural network［J］.Neurocomputing，2000，30(1):219-232.

［5］Yat-Fung Yam，Chi-Tat Leung，Peter K S Tam，et al.An independent component analysis based weight initialization method for multilayer perceptrons［J］.Neurocomputing，2002，48(1):807-818.

［6］Castellano G，Fanelli A M，Pelillo M.An iterative pruning algorithm for feedforward neural networks［J］.IEEE Transactions on Neural Networks，1997，8(3):519-531.

［7］Scott Fahlman，Christian Lebiere.The cascade-correlation learning architecture［J］.Advances in Neural Information Processing Systems，1991，2:524-532.

［8］Lauret P，Fock E，Mara T A.A node pruning algorithm based on a Fourier amplitude sensitivity test method［J］.IEEE Transactions on Neural Networks，2006，17(2):273-293.

［9］Zhihong Yaoa，Minrui Feia，Kang Lic，et al.Recognition of blue-green algae in lakes using distributive genetic algorithm-based neural networks［J］.Neurocomputing，2007，70(4):641-647.

［10］Leung F H F，Lam H K，Ling SH，et al.Tuning of the structure and parameters of a neural network using an improved genetic algorithm［J］.IEEE Transactions on Neural Networks，2003，14(1):79-88.

［11］Ehsan Valian，Shahram Mohanna，Saeed Tavakoli.Improved cuckoo search algorithm for feedforward neural network training［J］.International Journal of Artificial Intelligence and Applications，2011，2(3):36-43.

［12］Packianather M S，Drake P R，Rowland S H.Optimizing the parameters of multilayered feedforward neural networks through Taguchidesign of experiments［J］.Quality and Reliability Engineering International，2000，16(6):461-473.

［13］G B H，Qin-Yu Z，Chee-K S.Extreme learningmachine:theory and applications［J］.Neurocomputing，2006，70(1):489-501.

［14］HUANG Guangbin，ZHU Qinyu，Siew C K.Extreme learning machine:a new learning scheme of feedforward neural networks［C］//Proceedings of 2004 IEEE International Joint Conference on Neural Networks.Budapest，Hungary:IEEE，2004，2: 985-990.

［15］YUAN Lan，Yeng Chai Soh，HUANG Guangbin.Constructive hidden nodes selection of extreme learningmachinefor regression［J］.Neurocomputing，2010，73(16/18):3193-3199.

［16］WANG Yuguang，CAN Feilong，YUAN Yubo.A study on effectiveness of extreme learningmachine［J］.Neuro-Computing，2011，74(16):2483-2490.

［17］Castillo E.Functional networks［J］.Neural Processing Letters，1998，7(3):151-159.

［18］Castillo E，Cobo A，Gómez-Nesterkin R，et al.A general framework for functional networks［J］.Networks，2000，35(1):70-82.

(責任編輯:邢寶妹)

Active Functions Learning Neural Netw ork

YANG Shaoming，WANG Yalin*，WANG Meiyun，HE Haiming，LIYonggang
(School of Information Science and Engineering，Central South University，Changsha 410083，China)

In this paper，a novel neural network is proposed，whose active functions can be learned.Its active functions are not given and cannot be changed，but can be learned by the problems and could be the linear combination of any linear independent basis functions.The networks could be learned by tuning the coefficients of the basis functions.For the convenience of structure optimization，the input vectors of neurons are alwaysmapped to be scalar variables.In this paper，two quick learning algorithms are proposed for this network which does not need iterative procedures.The results show that this network has good function approximation capacity and fast learning speed.

neural network，active function，quick learning algorithms

TP 183

A

1671－7147(2015)06－0689－06

2015－07－25;

2015－09－28。

國家自然科學基金項目(61273187);國家自然科學基金創新研究群體科學基金項目(61321003)。

楊少明(1990—)，男，河南三門峽人，控制科學與工程專業碩士研究生。

*通信作者:王雅琳(1973—)，女，廣東惠州人，教授，博士生導師。主要從事復雜過程建模、優化與控制研究。Email:ylwang@csu.edu.cn